LA MATEMATICA DIVINA

Indagine intorno alle matrici del mondo e dell’ente intramondano in quanto “numero e misura”

Parte Seconda:

SULLA CORRELAZIONE FRA LA COSTELLAZIONE DEL CIGNO E IL PLATEAU DI GIZA E IL SUO POSSIBILE RAPPORTO CON LE TEORIE DI BAUVAL E LE RECENTI SCOPERTE DI CHARLES MARCELLO

A papa Francesco, e al suo tentativo di far rinascere

lo spirito del cristianesimo occidentale.

La historia agrega que, antes o después de morir, se supo frente a Dios y le dijo: « Yo, que tantos hombres he sido en vano, quiero ser uno y yo ». La voz de Dios le contestó desde un torbellino: « Yo tampoco soy; yo soñé el mundo como tú soñaste tu obra, mi Shakespeare, y entre las formas de mi sueño estabas tú, que como yo eres muchos y nadie ».

J. L. Borges

Devant une neige, un Être de beauté de haute taille. Des sifflements de mort et des cercles de musique sourde font monter, s’élargir et trembler comme un spectre ce corps adoré; des blessures écarlates et noires éclatent dans les chairs superbes. Les couleurs propres de la vie se foncent, dansent, et se dégagent autour de la vision, sur le chantier. Et les frissons s’élèvent et grondent, et la saveur forcenée de ces effets se chargeant avec les sifflements mortels et les rauques musiques que le monde, loin derrière nous, lance sur notre mère de beauté, – elle recule, elle se dresse. Oh! nos os sont revêtus d’un nouveau corps amoureux.
O la face cendrée, l’écusson de crin, les bras de cristal! le canon sur lequel je dois m’abattre à travers la mêlée des arbres et de l’air léger!

A. Rimbaud

UNA BREVE PREMESSA INTRODUTTIVA

1. La teoria della correlazione fra Orione e il paesaggio sacro di Giza e dintorni è attualmente una delle nozioni di archeologia e archeoastronomia fra le più note al mondo. Oltre agli archeologi e agli archeoastronomi di professione, molti milioni di semplici appassionati ne sono arrivati in vario modo a una più o meno approfondita conoscenza, al punto che oramai fa parte di quello che potremmo definire come il senso comune dell’archeologia alternativa.

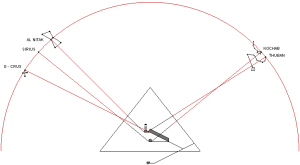
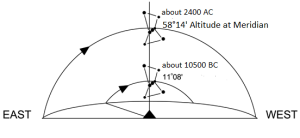
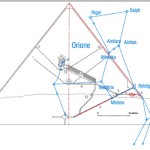
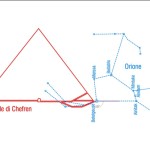
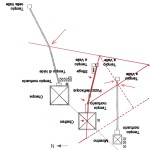
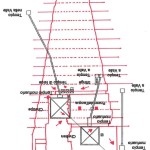
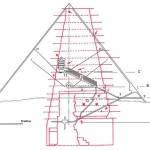
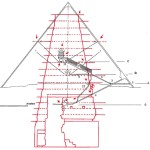
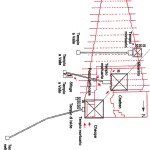
Com’è noto, nella sua estensione e nella sua complessità questa teoria (a volte definita semplicemente con l’acronimo OCT, Orion Connection Theory), è frutto del lavoro di Robert Bauval, anche se il primo a intuire una connessione fra la Grande Piramide e Orione fu Alexander Badawy. Questo archeologo, con la collaborazione dell’astronoma Virginia Trimble, dimostrò che i cosiddetti “pozzi di aereazione” della Camera del Re erano in realtà dei mirini astronomici. In una data attorno al 2500 a.C. il pozzo sud puntava su Alnitak – la stella più luminosa della Cintura di Orione – quello nord su Thuban – la stella polare dell’epoca

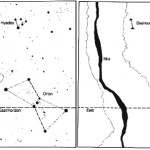
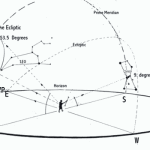
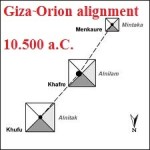
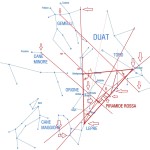
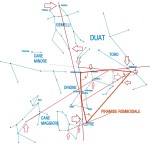
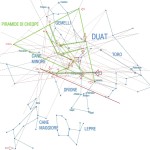
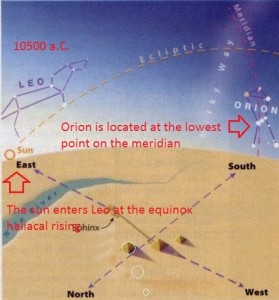
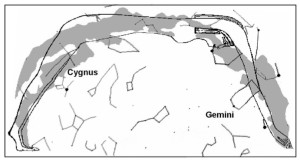
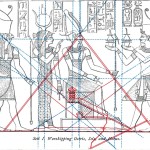
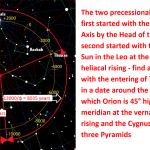
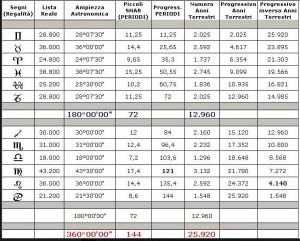
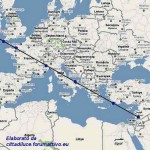
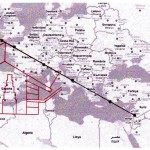
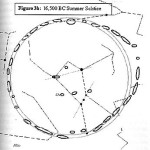
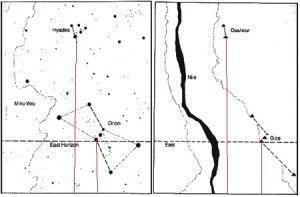
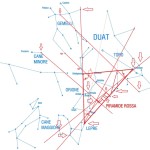
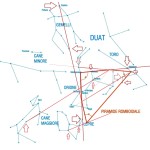
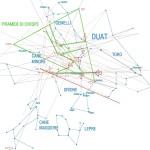
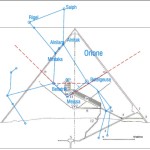
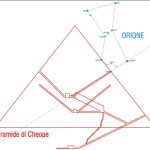
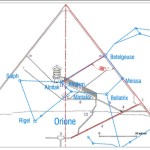
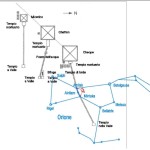
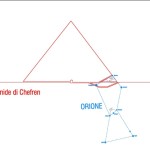
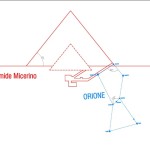
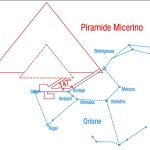
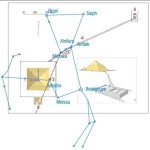
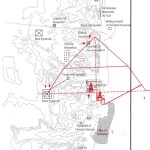
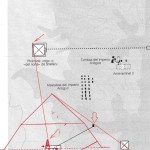
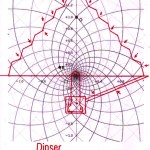
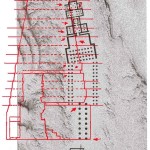
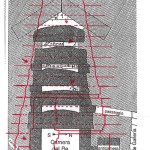
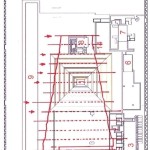
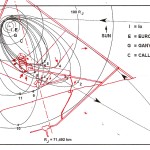
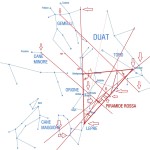
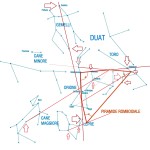
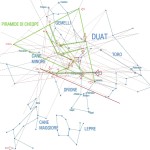
Le due altre correlazioni che vediamo nell’immagine, ovvero le stelle su cui puntano i cosiddetti “condotti di aerazione” della Camera della Regina, furono scoperte dallo stesso Bauval. Ma, come noto, la Orion Connection Theory è molto più articolata e complessa di così. Al di là della connessione con Orione di quelli che d’ora in avanti chiameremo “Pozzi Stellari”, in essa si sostiene che tutte le Piramidi della IV e della V Dinastia fanno parte di un gigantesco paesaggio sacro, che altro non sarebbe che una rappresentazione architettonica del cielo del Duat così come si presentava all’alba di un equinozio di primavera del 10500 a.C. circa. Il punto forte di questa argomentazione è che le tre Piramidi maggiori di Giza sono disposte sulla Terra come le tre stelle della Cintura di Orione furono disposte in cielo in quella data: la stessa in cui il sole entrò nel Leone all’alba dell’equinozio di primavera e in cui Orione raggiunse il punto più basso sul meridiano di Giza. Le immagini che rappresentano questa teoria si sono moltiplicate via via che diventava più celebre e autorevole. Alcune di esse, se possibile, sono diventate ancora più famose della teoria stessa

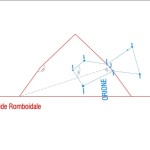
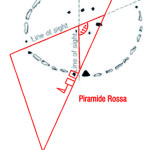
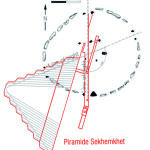
Nel corso della nostra esposizione, noi aggiungeremo altri elementi probatori alla tesi di Bauval, oltre a quelli che abbiamo già esposto in The Snefru Code parte 5. Fra l’altro, anche delle prove geometriche che ci dimostrano come almeno tre delle cinque Piramidi della cosiddetta IV Dinastia si possono ricostruire sulla base del cielo del Duat, a cui esse in vario modo sono riferite. Infatti, se noi consideriamo – per così dire – le stelle di questa parte di cielo come una sorta di puzzle, unendole con delle linee, secondo certi criteri, alla fine quelle che vengono fuori sono le proporzioni fondamentali della Piramide Rossa, della Piramide Romboidale e della Grande Piramide. In quest’ultimo caso, le finezze della ricostruzione sono veramente impressionanti. Il ritmo geometrico della disposizione delle stelle del Duat sembra, per paradosso, ricopiato da quello della Piramide. La sensazione che sul momento si può avere è quella di una strana sorta di miracolo astronomico

Lo stupore che si può provare di fronte a fenomeno di questo genere fa insorgere nello spirito la tentazione di lasciarsi andare immediatamente a facili esclamazioni e ad ancor più facili commenti. Ma noi abbiamo preferito riservare la trattazione di questo argomento alla fine del nostro lavoro. Sarà il momento in cui l’analisi sistematica dei problemi matematici connessi ai cicli cosmici misurati per mezzo delle Piramidi ci avrà aperto la strada a una più profonda comprensione del possibile senso teologico delle, chiamiamole così, Piramidi Cosmiche che si possono individuare nel cielo del Duat. Ma, certamente, una cosa che appare fin da subito chiara è che, se queste immagini dimostrano qualcosa, è che le tesi della Orion Connection Theory hanno un fondamento astronomico ben più solido e profondo di quanto non si fosse fino ad oggi creduto.

2.

Però, per parte nostra, ci sentiamo senz’altro di affermare che le tesi di Bauval, anche al momento in cui furono per la prima volta esposte al pubblico, apparivano senz’altro del tutto ragionevoli e molto ben fondate. Non ostante ciò, la loro radicale novità ha suscitato delle polemiche. Da parte dell’egittologia di stampo conservatore c’è stato, e in molti casi ancora oggi a continua a esserci, l’aprioristico rifiuto del metodo archeoastronomico tout court, che viene messo all’indice, quando non in ridicolo, tanto per datare le Piramidi quanto per ricostruire il loro significato storico e culturale. L’argomentazione che si porta ha, se non altro, il pregio e il merito d’esser chiara e concisa: che cosa potevano saperne dei bruti, appena usciti dall’Età della Pietra, di precessione, tempi cosmici, di stelle e allineamenti con le stelle? In effetti, secondo l’egittologia e gli egittologi “scolastici”, anche solo prendere in considerazione un’ipotesi del genere è un atteggiamento del tutto assurdo. Dal loro punto di vista, sarebbe come se fra qualche migliaio di anni un futuro archeologo, scoprendo che molte cucce per cani hanno la porta orientata verso la casa del padrone, ne deducesse che siano state i cani a costruirle in questo modo, per render gloria a chi tutti i giorni gli portava la zuppa e gli lanciava il bastone per farglielo riportare.

Ma, a ben vedere, questa “argomentazione” non risulta da un’analisi dei fatti, che verso ben altre conclusioni condurrebbero. È solo una deduzione a priori, il cui fondamento sono null’altro che i nostri pregiudizi evoluzionisti. Infatti l’evoluzionismo, nato come teoria per esplicare il ritrovamento di resti fossili di animali estinti, col tempo si è trasformato in un dogma di tipo religioso, cieco a qualsiasi fatto che possa contraddirlo. Oggi siamo arrivati a un punto che possiamo parlare tranquillamente di una sorta di blocco psicologico, che impedisce alla cultura “ufficiale” di essere anche solo sfiorata dal pensiero che «i nostri antenati del lontanissimo passato fossero dotati di menti affatto paragonabili alle nostre, e fossero capaci di processi razionali, sempre considerando i mezzi a loro disposizione. È sufficiente dire che ciò si scontra con un abito mentale che è già diventato seconda natura» (G. de Santillana – H. von Dechend, Il Mulino di Amleto, Adelphi, p. 94).

3.

Ma noi abbiamo ben considerato i mezzi a disposizione dei nostri padri, e abbiamo scoperto che erano non solo paragonabili ai nostri, ma addirittura ben superiori, tanto a un livello tecnico-scientifico che puramente matematico. Quindi, non solo abbiamo tutte le ragioni del mondo per esser certi che fossero dotati di menti superiori alle nostre, ma anche per ipotizzare che la loro scienza fosse molto più vasta e profonda di quella di cui disponiamo oggi. Una scienza dunque capace non solo di mettere a disposizione dei suoi possessori una tecnica ben superiore a quella attuale, ma anche più capace di rispecchiare l’intima essenza di cui si costituisce l’universo. Un’essenza che, secondo la Bibbia, proprio come secondo Keplero e Einstein, si definisce a partire da “numero, peso e misura“. Dunque i problemi che vediamo nello teorie di Bauval non nascono da un mancato riconoscimento della saggezza di nostri antenati.

Il fatto è che anche da parte di chi accetta il metodo archeoastronomico sono sorte delle critiche alle tesi di Bauval, dovute a quella che pare una certa imprecisione degli allineamenti. Per esempio, in una delle foto che abbiamo visto sopra vediamo un’inesattezza nella sovrapposizione fra la Piramide di Khafre e Alnilam. In altre ricostruzioni questa leggera imprecisione viene proiettata sulla sovrapposizione fra Mintaka e la Piramide di Menkaure. Ma, come vedremo successivamente, di punti deboli ve ne sono anche altri, e sono rimasti fino ad oggi del tutto inspiegati. Compito di questo scritto è risolvere questi problemi, offrendo un’immagine in cui Giza si mostrerà non solo come un generico paesaggio sacro, ma come una vera e propria meridiana precessionale. Uno strumento cioè, in grado di suddividere il ciclo precessionale in segmenti di diversa entità, connessi a quegli stessi numeri sacri con cui furono costruite le Piramidi: π, ɸ, il 10 e il numero di Eulero. La matematica coinvolta è dunque di livello altissimo, e avremo modo di rendercene conto nel corso della trattazione.

Giza sarebbe dunque nella nostra ipotesi – diciamo così – una sorta di gigantesco gnomone, destinato a misurare il trascorrere dell’eternità nel suo farsi Tempo e con ciò, come vedremo, ritmo, misura, proporzione. Viene spontaneo dire: nel suo farsi musica.

Non lo nascondiamo: il cammino che ci aspetta in queste pagine è duro e tortuoso, proprio come quello che abbiamo percorso nelle parti precedenti di questo lavoro. Ma chi avrà la pazienza di percorrerlo si incontrerà fin dal principio del cammino con cose che, fino a qualche tempo fa, anche i personaggi di un romanzo fantascientifico avrebbero definito fantascientifiche. Ma, naturalmente, in tutto il nostro lavoro non si potrà trovar traccia di un solo grammo di fantasia.

Noi infatti, come è oramai nostra consolidata abitudine, non trattiamo di ipotesi storico-archeologiche qualsiasi, ma solo di quelle che si fondino sulla logica inesorabile delle “matematiche dimostrazioni“. La nostra disciplina non è solo l’archeologia generale, ma anche e soprattutto qualcosa che potremmo definire archeomatematica, o archeogeometria. Essa dunque partecipa dello spirito del numero, la più alta forma di conoscenza che sia data all’essere umano.

Quindi, quel che troveremo di qui innanzi non è da considerarsi solo e principalmente come parte di una nuova immagine della storia, ma anche e soprattutto una nuova pagina della matematica e della scienza empirica. Quasi una rivoluzione si direbbe, che però, imprevedibilmente, ci viene incontro da un passato molto lontano, da abissi tempo di cui in questo momento pare difficile, per non dire del tutto impossibile, perscrutare il fondo.

Capitolo 1:

IL NUOVO CICLO COSMICO SCOPERTO DA CHARLES MARCELLO: SUE RELAZIONI ARMONICHE CON ALTRI CICLI COSMICI E CON IL CODICE DELL’ASTRONOMIA E DELLA GEOMETRIA SACRE

1.

Il nostro punto di partenza, come spesso succede nel campo della scienza empirica, sono proprio delle inesattezze metrologiche, che molti hanno giudicato trascurabili, o solo vagamente fastidiose, delle teorie di Bauval, che sono oggi riconosciute valide da una gran numero di studiosi. L’interna coerenza e la capacità esplicativa di questa possente visione archeoastronomica fanno sì che i suoi sostenitori vedano nei suoi detrattori delle persone ottuse o prevenute, se non proprio malintenzionate. Così ricorrono ad ogni mezzo per difenderne la validità contro quelli che si ritengono, in buona sostanza, solo dei pregiudizi. Pregiudizi che hanno dalla loro parte solo l’astratta ufficialità della cultura che li sostiene.

C’è da dire che questo è un fatto che si è verificato molto spesso. Ma a volte le critiche si fondano su altri presupposti. Le imprecisioni metrologiche oggettivamente rilevate, unite alla vastità e complessità delle strutture architettoniche di Giza e dintorni, quasi necessariamente erano destinate a generare delle teorie alternative, che potessero renderne ragione in modo più accurato o più dettagliato di quelle di Bauval. A Giza, su monumenti lunghi centinaia di metri, gli errori si misurano a volte in centimetri, ma più spesso in millimetri. Dunque, vedendo oggetti spostati di metri o, in certi casi, addirittura di chilometri rispetto alla loro posizione ideale, è facile che sorgano legittime perplessità, oltre che polemiche più o meno strumentali.

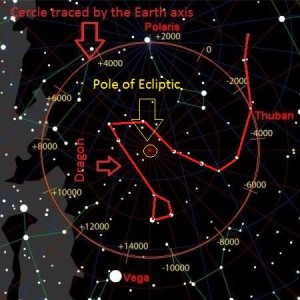
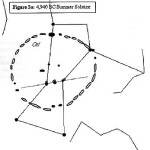
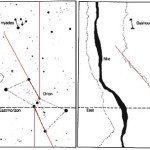
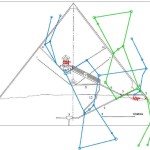
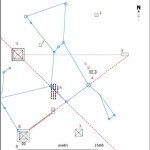
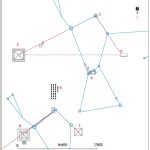
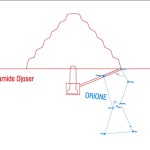
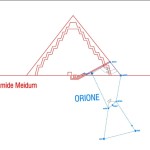
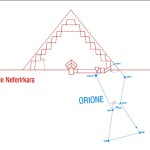
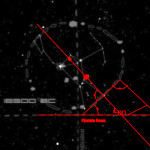
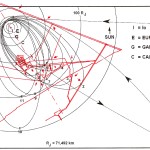
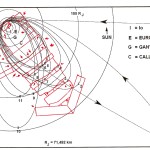
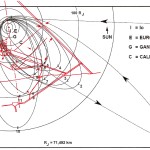
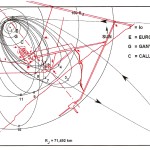
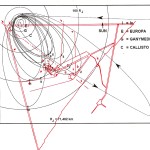
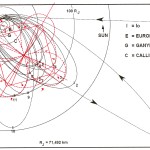
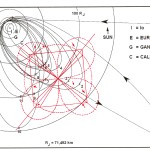
Recentemente, in un articolo su World Mysteries, Charles Marcello si spinge fino al punto di sostenere che l’allineamento fra le tre Piramidi e la situazione astronomica a Giza nel 10500 a.C. sia da considerarsi del tutto casuale. In controtendenza con un gran numero di specialisti e semplici appassionati, secondo lui Giza non ha nulla a che fare con Orione. Quello che in realtà sarebbe davvero importante è un allineamento fra le tre Piramidi maggiori e tre pianeti: Saturno, Venere e Mercurio. Sul piano della scala temporale, dobbiamo notare che l’allineamento individuato da Bauval si verifica ogni 26000 anni circa, ovvero al termine di ogni ciclo precessionale (e dunque anche all’inizio, visto che il ciclo precessionale è una ruota che si muove attorno a un punto fisso, il polo dell’eclittica). Invece, l’allineamento individuato da Charles Marcello, che possiamo osservare nelle foto qui sotto, si verifica a intervalli molto più brevi, vale a dire ogni 2737 anni

Questi 2737 anni, come ci apprestiamo a scoprire, sono straordinariamente interessanti da un punto di vista matematico. Molto al di là del fatto – che forse non è altro che una mera curiosità – che il 2737 è un numero non primo, che però è costituito soltanto da numeri primi (che tali sono il 2, il 3 e il 7).

Tanto per cominciare, 2737 anni sono pari a 2737 ∙ 365,25 = 999689,25 giorni. Una cifra la cui radice dodicesima corrisponde in pratica a √10

¹²√999689,25 = 3,16219575.. ≈ √10 = 3,162277660.. (-8,191.. ∙ 10^-5

Ma, a un livello di analisi più complesso, si può notare che questi 999689,25 giorni possono essere ottenuti per mezzo di una serie logaritmica a base 10, a partire da un’approssimazione di ɸ molto vicina a quella che fu codificata nella Grande Piramide. Come è noto, essa risulta dal rapporto fra le quattro facce triangolari e la base, ed è pari a ɸ_Cheope = 1,618590346..; aggiungendo 5 (che, lo ricordiamo, corrisponde a (ɸ + 1/ɸ)² = 5) a un’approssimazione di ɸ_Cheope vicinissima al valore rilevato, possiamo arrivare alla durata espressa in giorni solari del ciclo di Saturno, Venere e Mercurio. Siccome il passaggio richiede di fare per 3 volte l’inverso del logaritmo in base 10 del primo risultato che otteniamo, segnaliamo il ripetersi dell’operazione mettendo un 3 in basso a sinistra del simbolo, così che in questo caso, invece di scrivere per tre volte “inv. log”, scriveremo “₃inv. log”. Procederemo sempre in questo modo ogni volta che dovremo simbolizzare sequenze di logaritmi o inversi di logaritmi, siano essi naturali o in base 10

1/log [(5 + 1,618445150791..) ∙ 10^-10] = 1/log [(6,618445150791..) ∙ 10^-10] =

1/log 0,0000000006618445150791.. = 1/-9,1792440259294.. = -0,108941433213..

₃inv. log -0,108941433.. = 999689,25

Una cosa da sottolineare subito è che 5 + ɸ_Cheope = 6,618.. risulta un valore della costante di Planck compreso fra quello stabilito da Planck stesso all’inizio del secolo scorso (6,55) e quello attualmente considerato più esatto (6,626). Dunque, almeno su un piano storico, c’è stato senz’altro un momento in cui questo valore è risultato un valore esatto. Ma l’aspetto per noi più interessante viene fuori quando mettiamo in rapporto il ciclo di Saturno, Venere e Mercurio con altri cicli cosmici, che a livello religioso furono molto importanti nell’antichità.

Per prima cosa, possiamo notare che in questi 999689,25 giorni ci stanno un numero di anni delle eclissi (della durata pari a 346,6 giorni solari ciascuno) che risulta davvero molto particolare, anche se all’apparenza, come molto spesso ci è accaduto durante questa ricerca, sembra un numero qualsiasi. Eppure, già in prima istanza possiamo notare che esso si connette alla costante gravitazionale, sia pure in modo n po’ indiretto

999689,25 : 346,6 = 2884,2736583958453548759376803231

1/{[2884,273../10³ – 1] : π} = 1/(1,884273.. : π) = 1/0,599782.. = 1,667269.. ≈ 1 + G/10 = 1,6672

Ma molto più importante sembra il fatto che, come ci apprestiamo a scoprire, da esso si possono derivare con ottima approssimazione sia una discreta approssimazione di 1/ɸ_Cheope, sia il seno e dunque il coseno dell’angolo di 45°

³√[(2884,273658.. : 10³) – 1] : 2 = ³√1,884273658.. : 2 = 1,23513.. : 2 = 0,617567.. ≈ 1/ɸ_Cheope = 0,617821..

(⁸√2884,273658..) – 2 = 0,707101615.. ≈ sen 45° = cos 45° = 1/√2 = 0,707106781.. ( -5,166.. ∙ 10^-6

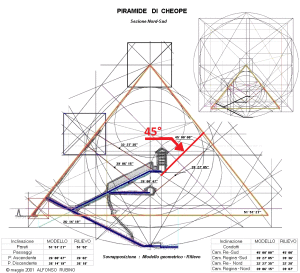
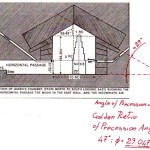
E qui dobbiamo ricordare che la declinazione di Orione sul cielo di Giza nel 2500 a.C. circa, era proprio di 45°. E il Pozzo Stellare Sud della Camera del Re che, in una data intorno a quell’epoca, va a inquadrare Alnitak, ha ovviamente questa stessa inclinazione

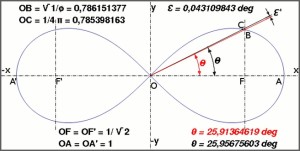
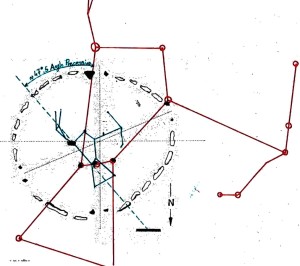
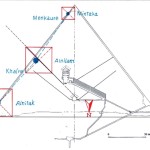
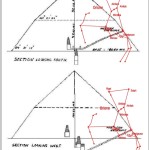
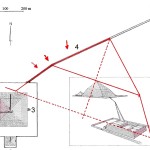
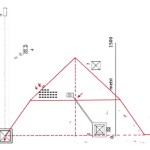
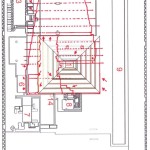
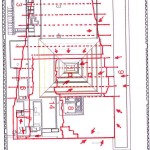
E qui sembra molto interessante notare che la somma degli angoli dei due Pozzi Stellari Nord – che secondo la ricostruzione che vediamo in questa immagine è pari a 71°33’50” = 71°,563888.. – va praticamente a coincidere con l’angolo di 71°,565051.., la cui tangente è pari a 3, uno dei numeri sacri più importanti, di cui non c’è nessun bisogno di sottolineare l’enorme ridondanza in tutte le religioni antiche e in molte di quelle attuali. La somma degli angoli dei quattro Pozzi Stellari è pari a 156°00’55” = 156°,0152777.., un angolo il cui coseno è pari a -0,913653..; questo valore corrisponde più o meno a quello della tangente della sezione aurea dell’angolo giro (tg 360°/ɸ = tg 222°,492.. = 0,916081..) moltiplicata per -1. Il corridoio discendente, con un’inclinazione pari a 26°14’19” = 26°,23861.., ha una tangente pari a 0,492898..; il suo logaritmo naturale è pari a circa 1/√(c – 1)

-1/Ln tg 26°,238611.. = -1/Ln 0,4928983.. = -1/-0,707452.. = 1,413522781.. ≈ √(c – 1) = 1,413479607..

Il corridoio ascendente ha un’inclinazione pari a 26°00’47” = 26°,013055..; la sua tangente è pari a 0,488014.., e il suo logaritmo naturale corrisponde a una cifra molto vicina a 1/³√e

-1/Ln tg 26°,013055.. = -1/Ln 0,488014.. = -1/-0,717409.. = -1,393903.. ≈ ³√e = 1,395612..

I dati li abbiamo tratti da quell’immagine che abbiamo visto sopra. Se consideriamo che nelle rilevazioni possa esservi un 2 o 3 per 1000 di errore, possiamo immaginare che i valori codificati per mezzo di questi angoli siano quelli esatti.

A ciò dobbiamo aggiungere che l’angolo di 45° ha anche una profonda connessione con una costante scientifica molto importante. Infatti, per mezzo del prodotto fattoriale, noi possiamo ricavarlo direttamente dal numero caratteristico della carica unitaria c_u = 1,6022, che qui sotto usiamo in un’approssimazione largamente consentita dal principio di indeterminazione

[(1/c_u )- c_u] ! = [(1/1,6021933553..) – 1,6021933553..] ! =

= (0,624144393.. – 1,6021933533) ! = -0,978048961..! = 45°

2.

E qui sembra importante osservare che una simile “proprietà transitiva verso l’archeologia” – se così possiamo definirla – la troviamo anche nel numero caratteristico della lunghezza di Planck ℓ_P = 1,616252, che sarebbe poi un quanto minimo di spazio al di sotto del quale il concetto di distanza non ha più alcun senso fisico. Infatti, anche da questo valore, strano a dirsi, siamo riportati in modo piuttosto diretto a delle nozioni connesse con la cultura Maya e Antico Egizia. Se prendiamo le approssimazioni di ℓ_P che vediamo qui sotto, possiamo ricavarne i 365 giorni del calendario solare Antico Egizio e Maya, oppure i 360 gradi dell’angolo giro (corrispondenti però ai giorni “puri” di quegli stessi calendari)

[(1/ℓ_P )- ℓ_P] ! = [(1/1,6160552895..) – 1,6160552895..] ! = -0,997264579493.. ! = 365

[(1/ℓ_P) – ℓ_P] ! = [(1/1,61602786062..) – 1,61602786062..] ! = -0,99722664786346..! = 360

In questo senso, la lunghezza di Planck si mostra capace di relazioni ancora più complesse. Infatti, se prendiamo l’approssimazione che vediamo qui di seguito e ne facciamo il prodotto fattoriale, otteniamo un numero da cui, attraverso il prodotto fattoriale di 360/π, possiamo ottenere 1

ℓ_P ! + ₄log [(360/π) !] = 1,616690452..! + ₄log (114,591.. !) =

= 1,447752245.. + ₄log 4,207365497.. ∙ 10¹⁸⁷ = 1,447752245.. + (-0,447752245..) = 1

E i qui cominciamo ad apprezzare in modo già piuttosto cospicuo una caratteristica molto importante del sistema matematico che stiamo analizzando: attraverso di esso, non c’è parte dell’universo che non sia connessa con un’altra: la declinazione di Orione in un momento topico del ciclo precessionale si può derivare dal valore della carica elettrica; dalla lunghezza di Planck si possono ricavare i numeri caratteristici del calendario solare Maya e Antico Egizio, uno dei quali è connesso con l’angolo giro.

Questo sembra un chiaro indizio che, procedendo nel modo che abbiamo appena visto, si possano ricavare ancora miriadi connessioni altrettanto significative. Infatti, andando avanti con questo metodo, quel che ci apprestiamo a scoprire è che da un’approssimazione della costante di Planck (6,626) possiamo ricavare ɸ; dal raggio classico dell’elettrone (r_e = 2,81777) possiamo ricavare 10/π; dalla sua massa (m_e = 9,1091) possiamo ottenere di nuovo il numero di giorni del calendario Antico Egizio e Maya (però questa volta moltiplicato per 10³). Infine, da un’approssimazione della massa del protone (m_p = 1,6725) possiamo ricavare di nuovo la carica unitaria e 10/π, mentre dal raggio del protone (r_p = 1,535), strano a dirsi, possiamo ricavare di nuovo il raggio del protone. Possiamo completare il quadro ricordando che G – 5 = m_p. Dunque, tutto quel che vediamo riguardo alla massa del protone vale anche per G.

(h – 1/h) : 4 = (6,623122.. – 1/6,623122..) : 4 = 6,472135.. : 4 = 1,618033.. = π

(r_e – 1/r_e) ! = (2,81581775.. – 1/2,81581775.. ) ! = 3,183098.. = 10/π

(m_e – 1/m_e) = (9,11232822.. – 1/9,11232822..) ! = 9,002586782..! = 365000 = 365 ∙ 10³

(m_p + 1/m_p) ! – 1 = (1,672084.. + 1/1,672084..) ! – 1 = 2,6022 – 1 = 1,6022 = c_u

m_p + m_p ! = 1,672108.. + 1,672108..! = 1,672108.. + 1,510999.. = 3,183098.. = 10/π

r_p !³ – 1 = 1,535655..!³ – 1 = 1,363512..³ – 1 = 2,535 – 1 = 1,535 = r_p

Il raggio classico del protone, che ha questa strana caratteristica di poter, per così dire, ritornare su sé stesso, è dunque molto vicino a quel numero in grado di soddisfare l’equazione armonica che vediamo qui sotto

x !³ – 1 = x = 1,5358023847..

Il tipo di relazione armonica che il raggio del protone stabilisce con la sua massa è piuttosto particolare, dato che, in pratica, la radice quinta di r_p = 1,535 corrisponde in modo praticamente perfetto alla radice sesta di m_p = 1,6725. Entrambe queste radici, corrispondono al rapporto m_p/r_p

⁵√r_p = ⁵√1,535 = 1,089486055.. ≈ ⁶√m_p = ⁶√1,6725 = 1,089501136.. ≈ m_p/r_p = 1,6725/1,535 = 1,089576547..

Ma qui possiamo notare che il valore di ħ che possiamo ricavare dal valore della costante di Planck che fu calcolato da Planck stesso all’inizio del secolo (6,55), elevato al quadrato, corrisponde con buona approssimazione (⁵√r_p)

ħ_Planck² = [h_Planck/(6,55/2π)]² = 1,0424648.. ² = 1,086733.. ≈ ⁵√r_p = 1,089486055..

Dunque, se “stiriamo” un po’ verso l’alto il valore di ħ_Planck, una cosa consentita tanto dal principio di indeterminazione tanto dal fatto che nel corso del secolo scorso il valore di h è cresciuto di circa 7/1000, questa sequenza armonica si amplia ulteriormente. In questo modo, scopriamo che il raggio e la massa del protone sono stati costituiti in modo tale da soddisfare la seguente equazione armonica (in cui ovviamente z = ħ_Planck; m_p = x; r_p = y)

z² = x/y = ⁶√x = ⁵√y

E qui dobbiamo soffermarci un attimo a definire, sia pure in modo un po’ vago e provvisorio, il concetto ora introdotto di “equazione armonica”. Chiameremo d’ora in avanti “equazione armonica” un’equazione in cui una x, sottoposta a una funzione più o meno complessa, ritorna su sé stessa come in un cerchio – come in questo caso. Oppure, quando i risultati di due diverse funzioni della stessa x sono perfettamente coincidenti. In questo senso, l’archetipo di tutte le equazioni armoniche può essere considerata la celeberrima 2 + 2 = 2 ∙ 2, che in simboli diventa x + x = x^x. Comprenderemo via via che andiamo avanti l’importanza di queste funzioni che, per altro verso, trovandoci in un sistema caratterizzato complessivamente da questo tipo di circolarità, tende a spiegarsi da sola. Vedrà bene il lettore come questo particolare tipo di equazione – come anche il prodotto fattoriale – saranno molto importanti nel corso della nostra esposizione. Queste operazioni infatti si riveleranno capaci di individuare relazioni all’interno del sistema della matematica divina che, prima facie, sembrano davvero incredibili.

3.

Abbiamo già avuto sopra un primo assaggio dell’importanza delle “equazioni armoniche”. Ma qui di seguito possiamo vedere esempi ancora più impressionanti. Possiamo cominciare con quella che, sulle prime, potremmo considerare come una mera curiosità. Ovvero con il fatto che il prodotto fattoriale della costante di Planck è pari a un numero del codice astronomico sacro, il 7, elevato alla quarta potenza, ovvero a un altro numero sacro, il 4. . L’approssimazione di h che usiamo qui sotto è leggermente superiore al valore oggi considerato più esatto (6,626), ma si tenga presente che sulle tabelle delle costanti che si trovano su internet ci sono anche valori che arrivano fino 6,63, e dunque sono superiori a quello che usiamo qui sotto

6,627455481..! = 2401 = 7⁴

Contrariamente a quanto possiamo credere, quello che abbiamo appena visto non è un incidente: andando avanti nel lavoro troveremo sistematicamente delle connessioni armoniche fra il codice astronomico sacro e i numeri fondamentali della scienza moderna. Parliamo di codice astronomico sacro, ma potremmo e anzi dovremmo parlare dunque di codice scientifico sacro. E che questa non sia affatto un’ipotesi così azzardata come sembra, ce lo dimostrano gli esempi che facciamo qui seguito, a partire dal numero negativo il cui prodotto fattoriale è in grado di darci la costante di Planck. Siccome, come abbiamo visto nei lavori passati, possiamo considerare il valore attualmente considerato più esatto come un estremo superiore, e quello calcolato da Planck stesso all’inizio del secolo scorso come un limite inferiore, li calcoliamo entrambi. Vedremo poi subito il perché

-32,123058..! = 6,6260596089563474249904167783191 ∙ 10^-34 = h

-32,124094..! = 6,5500582175016823529609266752451 ∙ 10^-34 = h_Planck

Ovviamente questi due numeri, per quanto molto simili, sono divisi da un piccolo intervallo. Ebbene, se prendiamo un valore intermedio e gli applichiamo la funzione x! ∙ -x!, abbiamo una prima sorpresa. Infatti, il risultato che otteniamo è 266, ovvero il numero delle particelle che i Dogon, ultimi eredi della sapienza ermetica Antico Egizia, considerano essere alla base dell’universo

-32,1238691948..! ∙ 32,1238691948..! = 266 numero di particelle elementari conosciute dai Dogon

Questo numero può essere ottenuto con approssimazione davvero molto buona per mezzo di ɸ nel modo che vediamo qui di seguito

10^2ɸ : 4ɸ = 10^3,236067.. : 6,472135.. = 266,084..

Il numero esatto è appena superiore a ɸ, e risulta pari a 1,617953883345..

10^{3,23590776668…} : 6,47181553338.. = 266

Se poi ci spostiamo sulla trigonometria, e andiamo a vedere le caratteristiche di un angolo il cui valore si trovi fra i due che abbiamo sopra calcolato, vediamo altre cose interessanti. Infatti, il suo seno è pari al numero caratteristico della costante che descrive il raggio della prima orbita dell’elettrone attorno al nucleo (1bohr = 0,531 ∙ 10^-10)

sen 32°,123869194785.. = 0,531751.. ≈ 1bohr = 0,531

Dalla sua tangente, con l’aggiunta di 2c = 5,9958492, giungiamo a un’approssimazione della costante di Planck molto particolare

tg 32°,123869194785.. + 2c = 0,627879497.. + 5,9958492 = 6,6237286973975196258773994863082

Abbiamo scritto per intero quest’approssimazione di h perché se la usiamo per dividere l’angolo giro, la somma di seno e coseno viene vicinissima alla radice cubica del numero di Eulero, e così pure la tangente. Il che significa che quest’angolo è vicinissimo a quel punto di unicità della trigonometria a base 360° in cui la tangente meno il seno e il coseno è uguale a 0

360° : 6,623728.. = 54°,35005213022159920309567457183

sen + cos 54°,35.. = 1,395424557.. ≈ ³√e = 1,395612425.. (-1,878.. ∙ 10^-4 ≈ 1/[10 ∙ (3/ɸ – 1)]⁴ = 1,879.. ∙ 10^-4

tg 54°,35.. = 1,394215792.. ≈ ³√e = 1,395612425..

4.

Simili caratteristiche sono possedute anche dal raggio classico dell’elettrone r_e = 2,8179492.. ∙ 10^-15 m. Infatti, se andiamo a vedere il numero negativo da cui lo si può ricavare attraverso il prodotto fattoriale, e poi ripetiamo l’operazione che abbiamo fatto sopra, ovvero gli applichiamo la funzione x! ∙ -x!, otteniamo un numero da cui, facendo la radice c = 2,9979246, possiamo ricavare il valore della costante di Planck così come fu calcolato da Planck stesso all’inizio del secolo scorso

-18,931872009..! = 2,8179492.. ∙ 10^-15 = r_e

^2,9979246√(-18,931872009..! ∙ 18,931872009..!) = ^2,9979246√ 280,019852.. = 6,550799.. = h_Planck

Osservando l’equazione che vediamo qui sopra, è del tutto chiaro che dal numero negativo da cui possiamo ricavare il raggio classico dell’elettrone, si può ricavare esattamente 280: per far ciò, ci basta alterare il valore del raggio classico dell’elettrone di un valore che rientra largamente nel principio di indeterminazione

-18,93186712.. ! = 2,817790.. ∙ 10^-15 = r_e

^2,9979246√(-18,93186712.. ! ∙ 18,93186712.. !) = ^2,9979246√ 280 = 6,550644.. = h_Planck

Ma 280 non è altro che l’altezza in cubiti della Grande Piramide: dunque questo parametro architettonico sacro si connette direttamente tanto al raggio classico dell’elettrone che a h_Planck che alla velocità della luce: e la complessità delle relazioni di cui è capace viene mascherata dal fatto che si tratta di un numero intero, dall’apparenza, diciamo così, del tutto anonima e innocua: ma proprio anonimi e innocui sembrano anche tutti gli altri numeri interi del codice astronomico sacro individuati da de Santillana e von Dechend.

Questi che abbiamo scoperto potrebbero essere considerati dei fatti stupefacente, ma, infine, si potrebbero anche considerare come coincidenze. Ma andando avanti nel lavoro scopriremo che qui non abbiamo a ch fare con coincidenze, ma con un sistema intelligibile e strutturato. Infatti, anche il raggio classico del protone (r_p = 1,535 ∙ 10^-18 m), per mezzo di questa stessa operazione, si trova in un’intima connessione con la Grande Piramide. Se moltiplichiamo il prodotto fattoriale del numero negativo con cui possiamo ricavare r_p per quello del suo valore positivo, la radice cubica del risultato che otteniamo non è altro che il prodotto dei valori di ɸ e di π che furono codificati nella Grande Piramide

-21,1685837.. = -1,535000513.. ∙ 10^-18 = r_p

³√-(-21,1685837..! ∙ 21,1685837..!)/π_Cheope = ³√131,635395../π = 5,086951../π_Cheope =

= 1,618575344.. ≈ ɸ_Cheope

Dunque, a questo punto, abbiamo già trovato degli indizi molto importanti della vastità e della complessità del nostro compito ermeneutico. Infatti, in un ciclo che riguarda Saturno, Venere e Mercurio, troviamo una neppure troppo nascosta allusione a quello di Orione. Questo implica una connessione anche con quello del Cigno che, come vedremo poi, si allinea alle Piramidi nella stessa data in cui Orione si trova a 45° di declinazione sul cielo di Giza. Ma, come abbiamo visto, questo angolo – che corrisponde anche a quello del Pozzo Stellare Nord della Camera del Re – ha a sua volta profondamente a che fare con la carica unitaria dell’elettrone e del protone. E, attraverso operazioni del tutto simili a quella con cui abbiamo scoperto la connessione del valore della carica unitaria con questa caratteristica metrologica della Piramide, abbiamo scoperto che altre sue caratteristiche metrologiche si connettono ad altri dati fisici riguardanti l’atomo: il raggio classico dell’elettrone e quello del protone.

Si noti inoltre che l’allusione all’angolo di 45° e dunque al ciclo di Orione, la si può cogliere attraverso l’interpolazione fra il ciclo di Saturno, Venere e Mercurio e un ciclo lunare molto importante, sia per l’astronomia sia per l’archeoastronomia.

5.

È del tutto ovvio che questo metodo di codificazione ermetico risulta talmente estraneo alla mentalità di un occidentale moderno che, sul momento, potrà sembrargli che le informazioni che abbiamo enucleato siano state estratte in modo arbitrario. Ma chi ha letto The Snefru Code parte 10, riconoscerà invece in questi calcoli qualcosa di molto familiare: ovvero il metodo con cui nelle misure della Camera del Re sono stati codificati tutti i cicli cosmici più importanti che riguardano la Terra, e tutte le costanti della nostra fisica. Le prove matematiche che abbiamo fornito in quella sede sono risultate infine inoppugnabili. Ma che questo accada non dipende, come già si è detto in quella sede, dall’abilità dei matematici e degli architetti Antico Egizi. Dipende invece dal fatto che il cosmo è stato costituito in modo tale che nei cicli cosmici siano codificate le leggi e le costanti di quella scienza matematica in grado di descriverli e di comprenderli in modo causale, anche se la causalità di cui in esse si fa uso non ci è per nulla familiare, almeno a livello di senso comune scientifico. Questa causalità infatti è connessa alla potenza del Numero, e non a quella di forze naturali, come siamo abituati a pensare nell’ambito della nostra cultura. In questo contesto, dobbiamo cominciare a pensare al Numero come alla forma stessa forza, e non come a un sistema di segni astratto in grado di descrivere una molteplicità di forze ad esso per principio del tutto estranee.

Ma, per chi voglia approfondire questa questione di filosofia della scienza, rimandiamo al lavoro già svolto in The Snefru Code parte 11. Qui ci conviene invece portare avanti il nostro lavoro di ermeneutica matematica e approfondire la relazione fra la durata dei cicli cosmici riguardanti più da vicino la Terra e la scienza in grado di descriverli. Questo perché, proseguendo in questa indagine, ci rendiamo conto che questa relazione non è monodirezionale, ma reticolare. Il che significa che certi numeri si connettono ad altri numeri per vie anche molto diverse. Per esempio, se si prende la durata dell’anno delle eclissi (346,6) e la si divide per 10³, poi facciamo il prodotto fattoriale, poi lo moltiplichiamo per 10 e poi facciamo ancora il fattoriale, si ottiene la velocità della luce misurata in chilometri al secondo.

(0,3466 ! ∙ 10) ! = (0,891502258.. ∙ 10) ! = 8,915022580..! = 299796,80.. ≈ c = 299792,46

Se facciamo la radice quadrata del prodotto fattoriale del numero dei giorni “puri” del calendario solare Antico Egizio (360) divisi per 10², quello che troviamo è la durata dell’anno solare (365,25 giorni) di nuovo divisa per 10²

√(3,6 !) = √13,381285.. = 3,6580.. ≈ 365,25/10² = 3,6525

Se facciamo la radice ottava del prodotto fattoriale della durata dell’anno solare (365,25 giorni) divisa per 10², e procediamo allo stesso modo con la durata totale del calendario solare Antico Egizio (365 giorni), in entrambi i casi quella che troviamo è un’ottima approssimazione della radice cubica del numero di Eulero

⁸√3,6525 ! = ⁸√14,416824.. = 1,395914120.. ≈ ³√e = 1,395612425..

⁸√3,65 ! = ⁸√14,365526844.. = 1,395292290.. ≈ ³√e = 1,395612425..

La media fra i due valori ci consente di ottenere un’approssimazione di ³√e che rasenta la perfezione

(1,395914120.. + 1,395292290..) : 2 = 2,79120641.. : 2 = 1,395603205.. ≈ ³√e = 1,395612425..

Anche da un numero sacro, che nel corso di questa ricerca diventerà molto importante, il 144, si può ricavare un valore vicinissimo ³√e

⁸√(144/10) = ⁸√14,4 = 1,395710390.. ≈ ³√e = 1,395612425..

Per altro verso, col prodotto fattoriale di ³√e possiamo ottenere una discreta approssimazione di ɸ_Cheope – 1

³√e ! : 2 = 1,395612425..! : 2 = 1,23862219.. : 2 = 0,619311.. ≈ ɸ_Cheope – 1 = 0,618590..

Naturalmente, ognuno può pensare di queste relazioni quello che vuole. Ma a noi sembrano un’altra prova che l’esperimento mentale iniziato a partire da The Snefru Code parte 3 ci conduce a scoprire una verità scientifica: ovvero che l’universo è un sistema ordinato e simmetrico, basato su funzioni di ɸ, π, del 10 e del numero di Eulero. Chi avrà la pazienza di seguire il lavoro che svolgeremo in questo articolo troverà infine che la trama di queste connessioni, che inizialmente può apparire confusa come un tappeto visto a rovescio, si risolverà infine in disegno ancora più splendido di quelli che abbiamo visto nei lavori passati.

6.

Dunque i cicli cosmici fondamentali che riguardano la Terra hanno senz’altro un profondo significato scientifico. Ma siccome essi si connettono in modo armonico con quello di Saturno, Venere e Mercurio, quel che ci dobbiamo aspettare e che puntualmente verificheremo è che anche questo ciclo porti impressa in sé la medesima forma che quegli altri che abbiamo già analizzato più profondamente. Infatti, se lo prendiamo in considerazione, invece che al livello del numero dei giorni, a livello del numero degli anni, vediamo che anche in questo modo incontriamo delle caratteristiche che sembrano davvero molto interessanti.

Per esempio, se eleviamo 2737 alla quinta potenza troviamo una discreta approssimazione del numero caratteristico della costante che descrive il raggio classico del protone (1,535) moltiplicata per 10¹⁷. Se la eleviamo alla ottava potenza troviamo una discreta approssimazione di π ∙ 10²⁷. Facendo infine il rapporto fra queste due cifre, troviamo un’approssimazione, di nuovo piuttosto soddisfacente, di (√ɸ)³.

2737⁵ = 1,535939.. ∙ 10¹⁷ ≈ r_p ∙ 10¹⁷ = 1,535 ∙ 10¹⁷

2737⁸ = 3,149186.. ∙ 10²⁷ ≈ π ∙ 10²⁷ = 3,141592.. ∙ 10²⁷

3,149186.. : 1,535939.. = 2,0503329 ≈ (√ɸ)³ = 2,058171.. (-0,00783807..

A un risultato quasi identico arriviamo facendo la radice ottava della differenza fra i 999689,25 giorni del ciclo di Saturno, Venere e Mercurio e la potenza di 10 che gli è più vicina, 10⁶

⁸√(10⁶ – 999689,25) = ⁸√310,75 = 2,0490445.. ≈ (√ɸ)³ = 2,058171027..

Già a questo livello il 2737 sembra contenere delle simmetrie di un certo spessore. Che diventano ancor più rimarchevoli quando scopriamo che interpretando numerologicamente la radice quadrata di 2737 come un angolo, arriviamo a un tipo di particolare di sezione aurea dell’angolo giro. Infatti, se lo dividiamo per 360, otteniamo una buona approssimazione di 1/ɸ_Cheope⁴

⁴√(√2737 : 360) = ⁴√(52,316345.. : 360) = ⁴√0,145323181.. = 0,617424309.. ≈ 1/ɸ_Cheope = 0,617821552..

A un risultato quasi perfettamente speculare possiamo arrivare facendo la radice ɸ³ di 2737e dividendola per 4

1/(^ɸ³√2737 : 4) = 1/(6,477844../4) = 1/0,617489.. ≈ 1/⁴√(√2737/360) = 0,617424.. (+0,0000653..

Quest’ultima simmetria che abbiamo sembra prima facie piuttosto complessa o addirittura un po’ cervellotica. Però non dobbiamo trascurarne il significato, perché essa è solo una delle tante caratteristiche armonico-trigonometriche che possiamo associare al numero d’oro. In questo caso, attraverso il ciclo di Mercurio, Venere e Saturno, ci siamo resi conto che l’angolo x in grado di soddisfare l’equazione armonica (4 ∙ x)^ɸ³ = (1/x⁴ ∙ 360)² è proprio un numero molto vicino a ɸ (e, ovviamente, il risultato è molto vicino a 2737).

Ma questo fatto possiamo considerarlo importante non in sé e per sé, ma come uno di quei molti casi in cui vediamo che alcune caratteristiche armoniche del numero d’oro si estendono in certi casi anche alle sue approssimazioni. Per esempio, il numero il cui inverso è uguale a numero stesso meno 1 e meno 1/1000, ovvero la x in grado di soddisfare l’equazione armonica che vediamo qui sotto, è un numero molto vicino a ɸ, e, in particolare molto vicino a ɸ_Cheope

1/x = x – 1 – 1/10³ = 0,61775768497247538477647144251762

x = 1,6187576849724753847764714425177 ≈ ɸ_Cheope = 1,618590346..

Anche il numero in grado di soddisfare l’equazione armonica che vediamo qui di seguito è un numero prossimo a ɸ: però corrisponde anche alla costante di Planck meno 5. E, lo ricordiamo, 5 può essere anche inteso come il risultato di (ɸ + 1/ɸ²)²

1/x = x – 1 – 1/10² – 1/10³ = 0,61500446228.. x = 1,62600446228.. ≈ h – (ɸ + 1/ɸ²)² = 1,626

Ugualmente, il numero in grado di soddisfare l’equazione armonica che vediamo qui di seguito è un numero prossimo a ɸ. Però è ancor più prossimo al numero caratteristico della lunghezza di Planck ℓ_P = 1,616252.. ∙ 10^-35 m. E il suo numero complementare risulta minore di (ɸ_Cheope – 1) = 0,618590346 di poco più di 3 milionesimi

1/x = x – 1 – 2/10³ = 0,618587133068.. ≈ (ɸ_Cheope – 1) = 0,618590346.. (-3,212931.. ∙ 10^-6

x = 1,616587133068.. ≈ ℓ_P = 1,616252..

Per altro verso, i 999689,25 giorni del ciclo di Mercurio, Venere e Saturno, anche se divisi per il numero di giorni dell’anno lunare (354,36), ci danno un risultato che, di nuovo, può sembrare del tutto banale, ma risulta invece molto interessante, dato che ci rivela una delle forse infinite proprietà armoniche di π.

999689,25 : 354,36 = 2821,1120047409414155096512021673

Infatti, se facciamo 2821,112../π⁶, il risultato che otteniamo è vicinissimo a quel numero che, diviso per π, è uguale al numero stesso meno 2. Ovvero, la x in grado di soddisfare l’equazione armonica che vediamo qui sotto

x/π = x – 2 = 0,9338844138485197199667896264673..

x = 2,9338844138485197199667896264673.. ≈ 2821,112.. : π⁶ = 2,93441201918395307.. (-5,27.. ∙ 10^-4

Dunque, già a questo livello di analisi, possiamo dire che il ciclo di Saturno, Venere e Mercurio individuato da Charles Marcello si connette in modo ermetico a due cicli lunari come anche al ciclo di Orione e del Cigno. Inoltre, esso si mostra come un numero connesso ad equazioni armoniche che hanno profondamente a che fare tanto con π e con ɸ. Ovvero, con i due numeri che sono alla base delle proporzioni della Grande Piramide e, come abbiamo oramai abbondantemente visto nei lavori precedenti, di tutto l’universo.

7.

Ma, appunto, la nostra analisi è solo all’inizio. Andando avanti ci prepariamo a scoprire per prima cosa che il ciclo scoperto da Charles Marcello ha una relazione armonica con un altro ciclo non molto noto, che sarebbe quello delle congiunzioni eliocentriche fra Giove e Saturno. Queste congiunzioni si verificano circa ogni venti anni (19,86); dopo, cioè, che Saturno ha percorso circa due terzi della propria orbita, mentre Giove percorre quasi due volte la propria. Per tre di questo congiunzioni occorrono circa 59,6 anni, un fatto che dà luogo a rapporti numerologici piuttosto interessanti, che sono stati ignorati anche dagli astronomi e dagli astrologi più raffinati. Infatti, se interpretiamo numerologicamente i 59,6 anni dei tre cicli come un angolo, scopriamo che esso ha un seno iperbolico praticamente pari all’inverso di ɸ² ∙ 10^-26

sinh x = 1/(ɸ² ∙ 10^-26) = 3,81966011.. ∙ 10²⁵ x = 59°,597935..

Inoltre, i 19,86 del singolo ciclo risultano in modo piuttosto ben approssimato dalla tangente dell’angolo di 59°,6 nel modo che segue

(1 + tg 59°,6)³ = (1 + 1,704458..)³ = 19,780673.. ≈ 19,86 (-0,08

Le 3 congiunzioni si compiono quando Saturno ha completato 2 rivoluzioni e Giove 5, con il 2 e il 5 che sono rispettivamente il terzo e il quinto numero della serie di Fibonacci: e il rapporto 3/5 è una costante geometrica molto importante, dato che è quella che ci serve per passare dai gradi espressi in sessantesimi a quelli espressi in centesimi.

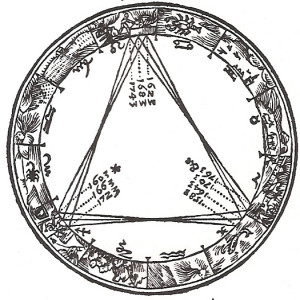
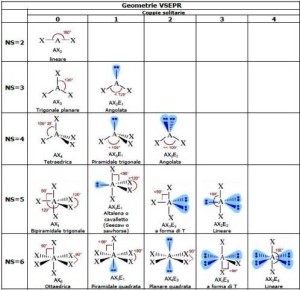
Dopo tre congiunzioni, la quarta si verifica quasi nello stesso punto della fascia zodiacale, mentre le due intermedie si verificano a intervalli di circa 120° nel cerchio dello zodiaco. In questo modo individuano nel piano dell’eclittica uno schema triangolare molto simile al triangolo equilatero, detto “trigono”, che possiamo vedere nella figura qui sotto

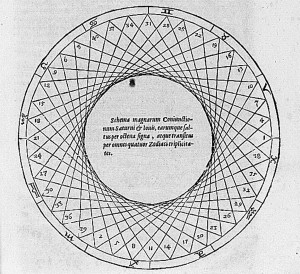
Keplero nello studio di successive congiunzioni di Giove e Saturno, fu colpito dal fatto che, dopo tre congiunzioni, queste si ripetevano sfasate nello zodiaco di un angolo costante in senso diretto, in modo tale che i segmenti tracciati tra i successivi punti di congiunzione tra i due pianeti davano luogo a un cerchio di tipo molto particolare, che gli dette il primo spunto per la redazione del celebre Mysterium Mundi

A pagina 164 de “Il Mulino di Amleto” de Santillana ci spiega che per percorrere tutto lo zodiaco questo triangolo cosmico impiega circa 2400 anni. Visto che de Santillana ci lascia la libertà di un “circa” noi, a mo’ di esperimento mentale, scegliamo di sostituire questo “circa” con un numero molto lungo e molto strano, che è quello che vediamo qui sotto. Vedremo immediatamente le ragioni di questa scelta

2397,9535964058079457502890510913

Un primo aspetto interessante di questa cifra è che la sua radice sedicesima non è altro che la costante di Planck meno 5 (ricordiamo che 5, che è un numero sacro, può essere scritto come (ɸ + 1/ɸ)²)

¹⁶√2397,953596.. = 1,626447.. ≈ h – 5 = 1,626

Ma l’aspetto più interessante di questo risultato sembra un altro. Infatti, se adesso moltiplichiamo la durata del ciclo individuato da Charles Marcello per la durata di questo delle congiunzioni di Giove e Saturno, noi vediamo che il risultato non è altro che la x in grado di soddisfare l’equazione armonica che vediamo qui di seguito.

¹⁶√x = [(²⁴³√x – 1) ∙ 10] + 2 = 2,6672868463216924637755198537257 ≈ 2 + G/10 = 2,66725

x = 2737 ∙ 2397,9535964058079457502890510913 = 6,563198993362696347518541132837 ∙ 10⁶ ≈

≈ h_Planck ∙ 10⁶ = 6,55 ∙ 10⁶

Quest’equazione armonica, come abbiamo visto, ha almeno due aspetti che paiono scientificamente importanti: il primo è che il suo risultato non è altro che 2 più la costante gravitazionale divisa per 10. Il secondo, è che la x in grado di soddisfare l’equazione è molto vicina al numero caratteristico della costante di Planck individuato da Planck stesso all’inizio del secolo scorso (anche se moltiplicato per 10⁶). Entrambi questi risultati ci confermano per l’ennesima volta l’esistenza di un sistema matematico unitario e onnicomprensivo attraverso cui la Mente Divina ha strutturato tanto l’infinitamente grande che l’infinitamente piccolo.

L’esistenza di questo che possiamo definire come un sistema armonico universale sembra dimostrata in modo inoppugnabile dal fatto che relazioni come quelle che abbiamo appena individuato sono una caratteristica tanto dei “numeri” dei cicli cosmici quanto delle costanti della fisica – che purtroppo però nei lavori scorsi non abbiamo avuto il tempo per analizzare altro che nel loro aspetto più propriamente trigonometrico. Ma invece, come in parte abbiamo già cominciato a constatare, questi che sono i numeri più importanti della nostra scienza intessono fra di loro una trama di simmetrie che va ben al di là della loro proiezione sul cerchio. In questa sede ci occuperemo, sia pure in modo non nel modo approfondito che sarebbe necessario, di queste meravigliose “trame armoniche”, anche perché una di essa va a intersecarsi in modo perfetto con il lavoro che stiamo facendo su questo ciclo astronomico scoperto da Charles Marcello. Ci apprestiamo a dimostrarlo nel capitolo successivo di questo lavoro.

Capitolo 2:

RAPPORTI ERMETICI FRA I CICLI COSMICI E LE COSTANTI DELLA FISICA: LA CODIFICAZIONE DELLA COSTANTE GRAVITAZIONALE NEL CICLO DI SATURNO, VENERE E MERCURIO

1.

Il punto di partenza obbligato di questo ragionamento è un qualcosa che sul momento può sembrare aver poco o nulla a che fare con l’analisi delle significato archeoastronomico del Plateau di Giza, ovvero con l’analisi dell’interna struttura matematica della costante gravitazionale G. Andando avanti nel lavoro, ci accorgeremo che questa analisi non solo risulta vitale in relazione al significato del Plateau di Giza, ma anche alla comprensione dell’intima struttura matematica dei cicli cosmici stessi e della scienza matematica che li descrive.

Per intraprendere la nostra analisi ci serviremo di un’approssimazione della costante di Newton che abbiamo, per così dire, fabbricato ad arbitrium. Noi la useremo solo ad un livello puramente matematico, ma il suo uso sarebbe perfettamente giustificato anche dal punto di vista sperimentale perché, come tutti sappiamo, il valore di G non si può rappresentare, almeno fino a questo momento, come un punto sull’asse delle x. Al contrario, le ricerche sperimentali effettuate ci dicono che il suo valore è particolarmente sfuggente. Infatti, a seconda dei metodi con cui si tenta di individuarlo, oscilla fra i 6,67 e i 6,673 ∙ 10^-11 newton ∙ m²/kg² circa.

Ebbene, il lato interessante di quest’approssimazione da noi scelta è che essa è estremamente utile per enucleare una straordinaria proprietà matematica dell’intorno matematico in cui si trova questa costante: infatti se ne facciamo il prodotto fattoriale, che quello che otteniamo è l’esatto valore di ɸ² ∙ 10³

6,671431667430154.. ! = 2618,033988749.. = ɸ² ∙ 10³

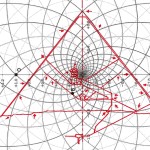
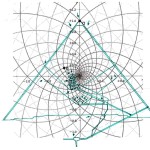
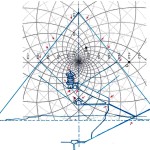
Dunque, in maniera del tutto imprevedibile, scopriamo che una costante scientifica della massima importanza ha profondamente a che fare con il numero d’oro: ovvero, proprio con uno dei valori che, assieme a π, risultano assolutamente fondamentali per la comprensione del Plateau di Giza. Una struttura le cui proporzioni si possono ben riprodurre attraverso il diagramma dello spazio-tempo che Zappalà ha costruito proprio per mezzo di un sistema di cerchi e di spirali logaritmiche

Il significato matematico di questa scoperta è al tempo stesso ampliato e confermato dal fatto che, prendendo un’altra approssimazione, che resta ugualmente entro i margini di variazione sperimentalmente accertati e accettati, ecco che scopriamo che il rapporto fra 11 – che è la potenza del 10 che caratterizza la costante – ed il suo numero caratteristico è esattamente uguale alla radice del numero di Eulero

11/6,6718372568389.. = √e = 1,648721270..

Che cosa può significare un fatto come questo? Ebbene, quel che sembra significare è che la Mente Divina, nel generare questo aspetto della complessa “armonia delle sfere” di cui si costituisce l’universo, si è servita come punto di riferimento armonico di ɸ e del numero di Eulero (oltre che dell’onnipresente 10, che troviamo in pratica in tutte le costanti elevato a una qualche potenza). Ma già a partire da The Snefru Code parte 10 abbiamo scoperto che la potenza-specchio della sezione aurea del 3 ci dà un’approssimazione di π che sfiora la perfezione^[1]. Dunque, il fatto che la costante gravitazionale si costituisca in un rapporto diretto con ɸ, significa che si costituisce anche in rapporto diretto π. E un’ulteriore connessione di questa costante con π lo scopriamo nel fatto che facendo il doppio prodotto fattoriale di √e quella che otteniamo è un’approssimazione di 1 + π_Cheope/10 che differisce dal valore esatto di poco più di un decimillesimo.

√e !! = 1,648721270.. !! = 1,314298733.. ≈ 1 + π_Cheope/10 = 1,3142857.. (1,301909242.. ∙ 10^-5

Il significato di questa relazione vede al tempo stesso rafforzato e ampliato il suo significato dal fatto che il triplo logaritmo in base della differenza che abbiamo registrato corrisponde a un’approssimazione di ɸ_Cheope /10 di poco superiore ai 10 milionesimi. Questo fatto prova in un modo che sembra assolutamente inconfutabile non solo il legame di G con ɸ, π e il numero di Eulero, ma anche quello che ɸ, π e il numero di Eulero intrattengono fra di loro

₃log 1/1,301909242.. ∙ 10^-5 = ₃log 76810,269.. = -0,161842653.. ≈ -ɸ_Cheope/10 = -0,1618590346..

Questo legame reticolare che abbiamo appena scoperto fra π, ɸ e il numero di Eulero ci da l’occasione di approfondire un aspetto della relazione fra π e ɸ che si crea attraverso la potenza-specchio di 3/ɸ che non abbiamo precisato negli articoli passati. Infatti, anche in questo caso la differenza fra l’approssimazione che otteniamo e il numero esatto è significativa: il che ci fa sospettare che, in generale, le minuscole differenze che riscontriamo nelle funzioni che legano questi valori fondamentali siano a loro volta delle funzioni approssimate di questi valori. Un qualcosa che potremmo definire dunque come una sequenza di approssimazioni periodiche.

Infatti, se facciamo per due volte il logaritmo in base 10 dell’inverso della differenza fra π e (3/ɸ)^3/ɸ il risultato è di nuovo un valore sperimentalmente ammesso di G meno 6: in questo modo il legame fra π, ɸ e la costante gravitazionale risulta ulteriormente rafforzato

₂log 1/[π – (3/ɸ)^3/ɸ] = ₂log 1/(2,033329.. ∙ 10^-5) = ₂log 49180,423.. = 0,671338.. ≈ G – 6 = 0,672

E qui dobbiamo sottolineare una cosa che anche nei lavori precedenti ci era sfuggita. Ovvero che la parte decimale di G – pari a 6,672 – 6 = 0,672 – praticamente corrispondente a quella della massa del protone 1,6725 – 1 = 0,6725 – ha un’importante corrispondenza con la misura espressa in cubiti dell’altezza totale della Grande Piramide. L’altezza totale è quella che comprende la parte invisibile, o sotterranea della struttura, ed è pari a 336 cubiti. Se moltiplichiamo questo numero per 2 e lo dividiamo per 10³, ecco che otteniamo G – 6

(336 ∙ 2)/10³ = 0,672

Inoltre possiamo notare che quell’approssimazione di G – 6 che abbiamo trovato sopra – 0,6713388.. – ha altre due caratteristiche che paiono notevoli. La prima è che da essa e da G possiamo ricavare un valore sperimentalmente possibile del numero caratteristico della lunghezza di Planck, nel modo che vediamo qui di seguito

1 + {⁸√[G – (G – 6)] : 2} 1 + [⁸√(6 – 0,672) : 2] = 1 + (⁸√5,328 : 2) =

= 1 + (1,232595.. : 2) = 1,616297.. ≈ ℓ_P = 1,616252..

La seconda è che, se eleviamo al quadrato questa cifra e facciamo il prodotto fattoriale del risultato moltiplicato per -1, quella che viene fuori è un’ottima approssimazione di ɸ: e questo sembra un altro filo con cui la costante gravitazionale si lega al numero d’oro. Un filo che riguarda anche la massa del protone, dato che un valore sperimentalmente possibile del suo numero caratteristico lo possiamo ricavare da G – 5 = 1,672

-{₂log 1/[π – (3/ɸ)^3/ɸ]}² ! = -(0,6713388..)² ! = -0,450695784.. ! =

= 1,618079040.. ≈ ɸ = 1,618033988.. (4,5051434326298649876602121102938 ∙ 10^-5

Abbiamo trascritto la differenza per intero perché non solo perché, come subito si vede, moltiplicata per 10⁴ essa va molto vicino al numero di cui abbiamo fatto il prodotto fattoriale, ma anche perché il suo inverso è ancora una volta un numero molto interessante. Infatti esso risulta molto prossimo a e¹⁰: in questo modo viene fuori per l’ennesima volta l’intimo legame fra i quattro numeri che furono codificati nella Grande Piramide: π, ɸ, il 10 e il numero di Eulero. Un legame che questa volta abbiamo potuto scorgere per mezzo dell’analisi della costante gravitazionale

Ln 1/4,505143.. ∙ 10^-5 = Ln 22196,851553.. = 10,007705735875172..

(4,505143.. ∙ 10^-5 ∙ -10⁴)! = -0,4505143..! = 1,617568.. ≈ ɸ = 1,618033..

2.

L’inverso della differenza che risulta da π – (3/ɸ)^3/ɸ, ha anche altre caratteristiche simmetriche che paiono rilevanti. Infatti, se facciamo per 4 volte il suo logaritmo naturale e poi lo sommiamo alla sua radice 81sima, otteniamo un valore molto prossimo a 1

₄Ln 49180,423.. = -0,14267450142266682864231520229387

⁸¹√49180,423.. + (-0,142674501..) = 1,142676672.. – 0,142674501..= 1,000002170617..

Fra l’altro, si nota che π – 3/ɸ ha un risultato abbastanza simile a ⁸¹√49180,423.. – ₄Ln 49180,423..

π – 3/ɸ = 1,287490687.. ≈ ⁸¹√49180,423.. – ₄Ln 49180,423.. = 1,2853511..

Dunque, una conseguenza che possiamo trarre da quanto abbiamo appena visto è che la differenza π – (3/ɸ)^3/ɸ risulta molto vicina alla x in grado di soddisfare l’equazione armonica che vediamo qui sotto

₄Ln x + ⁸¹√x = 1; x = 49178,613000617.. ≈ 1/[π – (3/ɸ)^3/ɸ] = 49180,423.. (+1,809999383..

E, di nuovo, ci troviamo di fronte a qualcosa che oramai non sembra più un’eccezione ma una regola. Infatti, anche in questo caso la differenza fra il numero esatto della x che vediamo sopra e 1/[π – (3/ɸ)^3/ɸ] sembra di nuovo un valore significativo. E questo a sua volta sembra significare che nell’ambito di questo sistema matematico le approssimazioni non sono un elemento di caos ma di ordine. È un po’ quello che accade a livello di astronomia quando ci troviamo a descrivere il sistema solare. Se definiamo “ideale” l’orbita della Terra intorno al Sole in quanto oggetto isolato, l’influsso degli altri pianeti ci viene spontaneo di considerarlo come una perturbazione. Ma se consideriamo come “ideale” il funzionamento del sistema solare nel suo insieme, ecco che allora che esso non è altro, per così dire, che un sistema di perturbazioni. Perturbazioni che a questo punto non possiamo più considerare appunto perturbazioni, ma parte essenziale della stabilità e del perfetto funzionamento del meccanismo. Che infatti, a quanto pare, resiste intatto da milioni o forse addirittura da miliardi di anni.

Nel nostro caso, abbiamo che le minuscole differenze che troviamo nelle equazioni diventano un modo della sua infinita ramificazione, o, come potremmo dire, della sua infinita interconnessione. Nel caso che stavamo trattando, ovvero la differenza fra x = 49178,613000617.. e 1/[π – (3/ɸ)^3/ɸ], se interpretiamo numerologicamente questa cifra come un angolo, scopriamo di nuovo una ramificazione molto importante, dato che quest’angolo ha un coseno iperbolico molto vicino a π, e una tangente iperbolica molto vicina all’inverso della costante di Dirac, 1/ħ

cosh 1°,809999383.. = 3,1370489; tanh 1°,809999383.. = 0,947831.. ≈ 1/ħ = 0,948252..

L’importanza per la struttura delle costanti fisiche di un valore come 3/ɸ viene confermata dal fatto che un angolo pari a (3/ɸ)² ha una tangente praticamente pari a c – 2

x = (3/ɸ)² = 1,8541019662496845446137605030969² = 3°,4376941012509463661587184907092

tanh 3°,4376941012509463661587184907092 = 0,9979363.. ≈ c – 2 = 0,9979246

Le indagini che stiamo conducendo ci portano a confrontarci con un fenomeno che appare tanto rilevante quanto piuttosto disorientante, a cui la nostra matematica non ci ha preparati.

Un numero importantissimo come π si può derivare da un altro numero importantissimo come ɸ. C’è una piccolissima differenza che però, se analizzata a fondo, si rivela ricca di significati matematici e scientifici, che si mostrano per vie nemmeno troppo complicate. Il lettore avrà notato che quasi sempre le radici o le potenze che operiamo risultano da due numeri fondamentali, il 2 e il 3, elevati a potenza. Per esempio, 9 risulta da 3², 27 da 3³, 81 da 3⁴, etc. Per quanto riguarda il 2, 8 risulta da 2³, 16 da 2⁴, 64 da 2⁵, etc. Quindi, anche queste potenze e queste radici che compaiono reiteratamente nelle nostre analisi, potrebbero essere legittimamente interpretate non come operazioni individuali, ma invece come sequenze di radici o potenze quadre o cubiche. Esse sono in questo modo direttamente associabili alle sequenze dei logaritmi, o degli inversi dei logaritmi, con cui oramai dovremmo esserci familiarizzati.

Ci troviamo dunque di fronte a un modo di considerare i numeri e i sistemi numerici diverso da quello a cui siamo abituati. Andando avanti, ci renderemo conto che anche il singolo numero può essere a sua volta considerato come una sequenza di numeri. Come una struttura dunque, e non come un punto sull’asse delle x. Dunque, arriveremo al punto che un numero come π potremo immaginarlo come una sorta di microcosmo, che nella sua intima struttura riflette l’intero mondo dei numeri.

3.

Ma, già a questo punto, ci sembra di poter dire che le relazioni che stanno venendo fuori sembrano di per sé piuttosto sconcertanti. Il numero caratteristico della costante di Newton che comprende nel suo margine di oscillazione sperimentalmente stabilito nulla di meno che il numero d’oro e il numero di Eulero! Chi l’avrebbe mai detto? Ci sarebbe di che rimanere davvero sorpresi, se non fosse che la vera sorpresa deve ancora arrivare. Abbiamo affermato sopra che in questo sistema anche le differenze tendono ad assumere un significato matematico e scientifico: di questa affermazione adesso possiamo fornire un’ulteriore prova, ancora più eclatante di quelle che abbiamo mostrato fino ad adesso.

Infatti, se facciamo il doppio logaritmo in base 10 dell’inverso della differenza fra quelle due approssimazioni della costante gravitazionale che abbiamo stabilito per via puramente astratta, per sottolineare la connessione di G con il numero di Eulero e con ɸ, quello che viene fuori è addirittura il numero caratteristico della costante che descrive il primo raggio dell’orbita dell’elettrone attorno al nucleo, 1bohr = 0,53 ∙ 10^-10

₂log [1/(6,6718372568389 – 6,671431667430154..)] = ₂log 1/0,000405589408746.. =

= ₂log 2465,547616472029462149726605376.. = 0,530444.. ≈ 1bohr = 0,53

A questo punto, ce ne rendiamo conto, sembra di aver a che fare con un qualcosa che potremmo definire come una sorta di romanzo di fantamatematica, più che con l’analisi delle relazioni fra i numeri che costituiscono l’ossatura della più seria e autorevole delle nostre scienze empiriche, ovvero la fisica in generale e la meccanica quantistica in particolare. Roba da Alice nel Paese delle Meraviglie, si vorrebbe dire. Ma, incredibilmente, quel che abbiamo visto non solo non è ancora tutto: non è nemmeno la parte più singolare.

Infatti, l’inverso di quel resto che abbiamo ottenuto fra le due approssimazioni di G che abbiamo stabilito sopra (ovvero quel 2465,54.. che abbiamo in parte analizzato), è molto vicino a un numero molto strano. Stiamo parlando di quel numero da cui possiamo sottrarre la parte intera facendo per due volte il logaritmo in base 10, che sarebbe poi la x in grado di soddisfare l’equazione armonica che vediamo qui sotto.

₂log x = x – 2464

₂log 2464,5304218084403612305485363694 = 0,5304218084403612305485363694.. =

= 2464,5304218084403612305485363694 – 2464 = 0,5304218084403612305485363694

In questo modo, scopriamo che il valore di 1bohr può essere calcolato in modo puramente astratto, in quanto risultato di un’equazione armonica che, come ci apprestiamo a vedere, contiene a sua volta almeno altri 3 valori importanti.

Infatti, se facciamo per due volte il logaritmo naturale di 2464,530.., otteniamo un risultato molto prossimo a (√ɸ)³, che infine risulta una funzione del numero caratteristico della lunghezza di Planck

₂Ln 2564,530.. = 2,055373.. ≈ (√ɸ)³ = 2,058171..

(³√2,055373..)² = 1,616567.. ≈ ℓ_P = 1,616258..

E qui è importantissimo sottolineare che la lunghezza di Planck, che è il fondamento della struttura spaziale del’universo, viene fuori in pratica ogni volta che si mettono in rapporto i parametri di protone ed elettrone (ma non solo quelli), come possiamo vedere qui sotto

³√(1bohr/r_e) : 2 = ³√(5,292 : 2,81777) : 2 = ³√1,87808.. : 2 = 1,233781.. : 2 = 0,61689.. ≈ ℓ_p – 1 = 0,616252..

(r_p/r_e)³ = (1,535/2,8179404) = 0,54472408..³ = 0,1616328.. ≈ ℓ_p/10 = 0,1616252..

(m_e/r_e) : 2 = 9,1091.. : 2,81794.. = 3,23253.. : 2 = 1,616969.. ≈ ℓ_p = 1,616 252

4.

E qui possiamo dare un’altra occhiata alle mirabilmente complesse ramificazioni del sistema. Infatti, qui sopra vediamo comparire il numero caratteristico della costante che descrivere il raggio classico del protone, come anche quello del raggio della prima orbita 1bohr = 0,53. Possiamo notare come sia possibile ottenere un’approssimazione praticamente perfetta di questi valori; nel caso di r_p = 1,535 sommando al numero di Eulero il suo doppio logaritmo in base 10; nel caso di 1bohr = 0,53, elevando il logaritmo naturale di π_Cheope = 22/7 alla potenza di π_Cheope

√[e + ₂log e] = √[2,718281828.. + (-0,362215688..)] = √2,356066139.. = 1,534948253.. ≈ r_p = 1,535

(Ln 22/7)^22/7 – 1= 1,145132..^3,142857.. – 1 = 1,530999.. – 1 = 0,530999.. ≈ 1bohr = 0,53

Il raggio classico del protone può essere ottenuto anche a partire da π_Cheope = 22/7 nel modo che vediamo qui sotto

[Ln (2 + Ln 22/7)]^{(2 + Ln 22/7)} = (Ln 3,145132..)^3,145132.. = 1,534517.. ≈ r_p = 1,535

In quest’ottica, dobbiamo notare che è possibile ottenere un’ottima approssimazione della lunghezza, di Planck meno 1 di nuovo in modo totalmente astratto, ovvero sottraendo c/10 al valore della tangente della sezione aurea dell’angolo giro. Per altro verso, è possibile ottenere un’ottima approssimazione di -c = -2,9979246 per mezzo di una funzione logaritmica di π. Il che, sapendo che da 1/(ɸ_Cheope – 1) si può ricavare la lunghezza di Planck, significa che possiamo ottenere una buona approssimazione della tangente di 360°/ɸ a partire da π e da ɸ_Cheope, facendo del tutto astrazione dai 360° dell’angolo giro

tg 360°/ɸ = 0,9160819155019..

0,9160819155019.. – 0,29979246 = 0,616289.. ≈ ℓ_P = 1,616252..

[log (π – 3) : (π – 3)] : 2 = -2,99789310.. ≈ -c = -2,9979246

1/(ɸ_Cheope – 1) + {[log (π – 3) : (π – 3)] : 20} – 1 = 0,916368046.. ≈ tg 360°/ɸ = 0,916081915..

Tutte queste circolarità armoniche che stiamo individuando ci informano e ci convincono via via in modo sempre più dettagliato e profondo quanto alla natura del sistema che stiamo indagando: tutti i numeri di fondamentali del sistema, siano essi geometrico-matematici o connessi con costanti della fisica, sono fra di loro interconnessi in modo tale che ognuno può essere, per così dire, ininterrottamente dedotto dagli altri. E non per caso stiamo insistendo particolarmente sulla lunghezza di Planck. Questo valore, molto prossimo al numero d’oro, è per noi molto importante perché le sue approssimazioni si legano quasi sempre in modo diretto alla Piramide. Come stiamo per vedere, da quella che abbiamo ottenuto da quel numero il cui doppio logaritmo naturale corrisponde alla sottrazione della sua parte intera, possiamo ottenere un valore che differisce da 1 – ɸ_Cheope di poco più di 4 milionesimi. L’importanza di questa connessione sembra accrescersi nel momento in cui ci rendiamo conto che l’inverso di questa differenza, esclusa la potenza del 10, corrisponde a sua volta a un valore molto vicino a ɸ_Cheope elevato al cubo

1/(³√2,055373..)² = 1/1,616567.. = 0,618594598.. ≈ ɸ_Cheope – 1 = 0,618590346.. (4,252252888.. ∙ 10^-6

³√1/4,252252888.. = ³√0,2351694.. = 0,617248.. ≈ 1/ ɸ_Cheope = 0,617821..

L’intimo rapporto fra la lunghezza di Planck e il valore di ɸ che fu codificato nella Piramide ci sembra a questo punto largamente dimostrato. Nel corso di questa indagine, prevedibilmente, lo incontreremo molte altre volte.

5.

E a questo punto il lettore avrà già compreso quali siano i motivi dell’estrema difficoltà di questo lavoro, che si riflettono purtroppo anche nel tentativo di esporlo in un modo ordinato e comprensibile. Il fatto è che da ogni valore di interesse si diparte una rete di relazioni simmetriche che lo legano a tutti gli altri valori di interesse, in un modo che ricorda molto da vicino una rete neuronale. Dunque, possiamo tranquillamente paragonare il funzionamento di questo sistema matematico a quello del cervello umano, dove il funzionamento di qualsiasi neurone dipende non solo da quello di tutti gli altri neuroni, ma – come in un circolo – anche dal proprio. Dunque, anche i “numeri” dei cicli cosmici che le Piramidi di Giza misurano fanno parte integrante di questo sistema, e la complessità del loro significato non può essere compresa al di fuori della complessità del sistema di cui fanno parte. È per questo che abbiamo accettato la difficilissima sfida di inserire l’analisi del loro significato nel contesto di un lavoro matematico enormemente più ampio e per di più complicatissimo: per far vedere quale sia il loro enorme significato scientifico, oltre che quello religioso.

Per avere un’idea della complessità del sistema che stiamo analizzando, ricordiamo che poco sopra abbiamo visto che l’inverso della differenza che abbiamo rilevato fra i due valori di G che abbiamo stabilito per sottolineare la sua dipendenza-connessione col numero di Eulero e colo numero d’oro (tale differenza era 1/0,0004055.. = 2465,5476..) risultava essa stessa significativa. Infatti, da essa abbiamo potuto derivare la lunghezza di Planck, il numero caratteristico della costante che descrive la prima orbita dell’elettrone, etc. A partire da queste relazioni ne abbiamo scoperte ancora altre, fra cui la sua vicinanza alla x (2464,530..) in grado di soddisfare un’equazione armonica molto particolare, in cui troviamo una x il cui doppio logaritmo in base 10 equivale alla sottrazione della parte intera, con il resto decimale che equivale a 1obhr.

Adesso, abituati come siamo a ragionare in percorsi deduttivi rettilinei, ci risulta difficile tornare a questo valore che avevamo già elaborato per vedere altre ramificazioni che da esso si dipartono verso altri valori significativi a livello sia fisico che puramente matematico. Eppure questo risulta indispensabile, perché altrimenti non siamo capaci di comprendere la natura profonda del sistema che, di fatto riflette nel suo insieme una caratteristica che troviamo in particolare nel numero d’oro. Il numero d’oro è cosiffatto che, per esempio, la differenza 1 – 1/ɸ non è altro che 1/ɸ². Il che significa che i resti delle funzioni di ɸ sono a loro volta delle funzioni di ɸ.

Piuttosto incredibilmente, una caratteristica del genere la ritroviamo nel sistema-universo nel suo insieme, anche se in modo più complesso. Infatti, se facciamo il doppio logaritmo naturale di 2465,5476../ɸ⁴, quello che otteniamo è un risultato vicinissimo all’inverso del doppio del logaritmo naturale di √π. Questo significa che se lo dividiamo per ɸ⁵ otteniamo un’ottima approssimazione della sezione aurea dell’angolo giro. Se poi lo dividiamo per ɸ¹⁰, arriviamo a un’ottima approssimazione di e^c

₂Ln (2465,5476..: ɸ⁴) = ₂Ln 359,718546.. = 1,772461.. ≈ √π = 1,772453.. (+7,58.. ∙ 10^-6

2465,5476.. : ɸ⁵ = 222,318288…. ≈ 360 : ɸ = 222,492235..

2465,5476.. : ɸ¹⁰ = 20,046427…. ≈ e^{c = 2,9979246} = 20,043894.. ≈ 15 + e^ɸ = 20,043165..

E qui potremmo andare ancora avanti e dimostrare, per esempio, che da 1/[π – (3/ɸ)^3/ɸ] possiamo ricavare per mezzo di π un’ottima approssimazione della sezione aurea del 13. Un valore che ha, come vedremo, delle profonde connessioni con l’interpretazione archeoastronomica del Plateau di Giza. Ma conviene forse fermarci qui, e cercare di ricapitolare, sia pur provvisoriamente, il senso del lavoro che abbiamo già svolto.

6.

Infatti, da quel che sembra di poter capire, nel generare la struttura matematica dell’universo la Mente Divina è partita da quei quattro numeri fondamentali che abbiamo individuato già a partire da The Snefru Code parte 3, ovvero da π, ɸ, il 10 e il numero di Eulero. Numeri che i nostri padri dovevano conoscere e nella loro natura come per altro anche nel loro significato matematico, scientifico e teologico, dato che sono a fondamento di quel libro sapienziale di pietra che è Grande Piramide.

Ma, per poter costruire una costante come G, la mente divina si è dovuta servire anche di un numero intero, cioè l’11, per ottenere quella potenza negativa del 10 in grado di collocarlo al giusto posto nella struttura matematica dell’universo. E qui dobbiamo notare che anche l’11 si può ricavare per via numerologica dalla misura del lato della Piramide espresso in cubiti: infatti dividendo il 440 per le decine – cioè per il 40 – otteniamo 440 : 40 = 11. Sembra dunque che il lato di base della Piramide sia profondamente connesso con la costante G, e dunque con la forza di gravità: una cosa molto importante questa a livello simbolico, dato che il lato è quello che si appoggia sulla terra, e che su essa lo fonda.

Il criterio con cui la Mente Divina ha scelto l’11, a quanto pare, è che dividendolo per il numero caratteristico della costante – che in realtà si muove entro un margine di oscillazione che ancora non ci è chiaro come sia stato stabilito – ci desse la radice del numero di Eulero.

D’altra parte, abbiamo scoperto che la Mente Divina non si è accontentata di questa connessione. Infatti, prendendo un numero vicinissimo a quello connesso con il numero di Eulero e facendo il suo prodotto fattoriale, abbiamo ottenuto ɸ² ∙ 10³.

Fra questi i due valori di G – l’uno connesso al numero di Eulero e l’altro a ɸ – vi è però, come abbiamo visto, un piccola differenza. Ma questa differenza, lungi dall’essere un difetto o uno scarto inutile, si connette armonicamente con uno dei valori del raggio della prima orbita dell’elettrone intorno al nucleo 1bohr: uno di quelli resi sperimentalmente possibili dal principio di indeterminazione.

Questo valore di 1bohr, derivato da G, è però in strettissima relazione con un altro valore possibile di 1bohr, cioè quello che si può dedurre da un’equazione armonica che, come abbiamo visto, sembra in stretta relazione con tre costanti geometriche e una costante fisica fondamentali.

Dunque il sistema in cui ci muoviamo lo possiamo definire super-simmetrico: l’ordine che in esso sembra regnare è talmente assoluto che non ci si meraviglia se fino ad oggi sia stato scambiato per un caos.

7.

Dato il contesto, noi possiamo immaginare che anche i resti delle approssimazioni di (√ɸ)³, √π, di 360/ɸ e di e^c che abbiamo trovato possano avere un significato. Però, in questo momento ci conviene svoltare in un’altra direzione che, come vedremo ben presto, ci riporterà dritti dritti all’argomento principe di questo lavoro, vale a dire il significato archeoastronomico del Plateau di Giza.

Infatti, se adesso andiamo a vedere la differenza fra il 2464,530421.. che abbiamo ricavato dall’equazione armonica e il 2465,547616.. che abbiamo ricavato dalle due approssimazioni di G – anch’esse ottenute da equazioni armoniche – ecco che scopriamo che il risultato è un numero, di nuovo, un po’ particolare. Infatti, elevandolo al cubo otteniamo un’approssimazione della costante di Dirac che ha delle caratteristiche piuttosto sorprendenti. Caratteristiche che, come presto vedremo, sono contenute in modo perfetto nella durata in anni solari del ciclo individuato da Charles Marcello

(2465,547616 – 2464,530421)³ = 1,0171946..³ = 1,0524760.. ≈ ħ = 1,054571..

Quest’approssimazione della costante di Dirac ha delle caratteristiche che abbiamo definito sorprendenti perché se la dividiamo per 2 noi ci rendiamo conto che essa è vicinissima, ma non identica, a quel numero che, moltiplicato per 2, è uguale al numero stesso diviso per 10 con l’aggiunta di 1; ovvero, alla x in grado di soddisfare l’equazione che vediamo qui sotto

x ∙ 2 = 1 + x/10

Ce ne possiamo rendere conto facendo la divisione

1,0524760.. : 2 = 0,526238.. ≈ (1,0524760.. – 1) ∙ 10 = 0,524760.. (0,001478..

Per solito, mettiamo il valore esatto della x che risolve le equazioni armoniche immediatamente dopo le equazioni stesse. Ma questa volta facciamo eccezione, e rimandiamo il calcolo del valore esatto al capitolo successivo dove vedremo che esso può essere dedotto in modo assolutamente perfetto dal ciclo astronomico scoperto da Charles Marcello. Il lettore può qui legittimamente domandarsi: perché dedicare un intero capitolo all’analisi di una sola relazione, per quanto interessante? La risposta a questo punto è oramai almeno in parte diventata ovvia. Perché il sistema in cui ci muoviamo abolisce del tutto l’idea di “singola relazione”. E nel prossimo capitolo avremo l’ennesima dimostrazione che avere a che fare con i numeri caratteristici della fisica, o dell’astronomia, è avere a che fare con una rete intelligente e incredibilmente raffinata di proporzioni armoniche, i cui limiti coincidono con quelli dell’universo.

I poli di questo sistema sono costituiti da degli intorni numerici che possiamo paragonare alle stelle nel cielo notturno: dei corpi minuti, che sembrano dei punti, ma che in realtà, in prossimità del loro limite esterno tendono a sfumare nel buio, senza che il loro confine possa essere definito in modo assolutamente esatto (il che non significa che non sia in qualche modo intuibile).

8.

In questo caso, abbiamo visto una serie di equazioni armoniche che si dipartono dalla costante gravitazionale che ci hanno portato infine nei pressi di un’altra equazione armonica, legata questa volta alla costante di Dirac. E da lì siamo ritornati al nostro punto di partenza, ovvero al ciclo di Saturno, Venere e Mercurio. Qui sotto possiamo vedere come un angolo importantissimo come quello di 60° si connetta ad altri valori molto importanti. Come prima cosa, da esso possiamo ricavare un’approssimazione della costante di Planck che in pratica coincide con quella che oggi viene ritenuta sperimentalmente più affidabile

√tg (60°/sen 60°) + (10 ∙ cos 60°) = √tg 69°,282032.. + (10 ∙ 1/2) =

= √2,643915412.. + 5 = 1,626012119.. + 5 = 6,626012.. ≈ h = 6,626

Come abbiamo appena visto, il coseno di 60° è pari a 1/2, un valore che può risultare da

cos 60° = log √10 = log 3,16227766.. = 0,5

Quindi, il coseno di 60° si lega a un altro valore matematico molto importante, √10, per mezzo del logaritmo in base 10. E fin qui siamo nel senso comune matematico. Però pochi sanno che √10 è vicinissima alla x in grado di soddisfare l’equazione armonica che vediamo qui di seguito, il cui risultato è appena diverso da quello cui possiamo arrivare per mezzo del logaritmo in base 10 di 6

(log x)² = 10^{cos x} = 3,16190826753066232.. ≈ (1 + log 6)² = 3,161821869.. ≈ √10 = 3,16227766..

x = 60°,003356468455..

L’angolo di 60° si connette anche a una cifra che ha una proprietà davvero molto curiosa, vale a dire a quel numero il cui logaritmo naturale è pari la numero stesso moltiplicato per -1. Facendo per due volte il logaritmo in base 10 di 1 + sen 60° ne otteniamo un’approssimazione che differisce dal numero esatto di meno di 20 milionesimi

Ln x ∙ -1 = x = 0,567143290.. ≈ ₂log (1 + sen 60°) = -0,567162857..

In un modo molto diverso, anche il coseno di 60° – che, come tutti sappiamo, è pari a 1/2 – assume una rilevanza, dato che se andiamo a vedere quale è il valore della in x in grado di soddisfare l’equazione armonica che vediamo qui sotto, scopriamo che si tratta di G – 6 alias m_p – 1. Notevole sembra anche il fatto che, attraverso una sequenza logaritmica mista – possiamo ottenere un’ottima approssimazione di questa x anche da π – 3

-(log x – 1/2) = x = 0,672383167.. ≈ G – 6 = 0,672 ≈ m_p – 1 = 0,6725 ≈ ₂log (₄inv. Ln -(π – 3) = 0,672309230..

E qui c’è da notare che questa equazione sembra molto importante perché essa costituisce un’altra relazione reticolare fra π, ɸ, il 10 e il numero di Eulero davvero prossima alla perfezione, anche se questa volta essa è supportata dal 3.

Ma, comunque sia, ancora più importante di questo sembra il fatto che, come vedremo meglio successivamente, cos 60° = 1/2 si connette a π perché il prodotto fattoriale del suo valore negativo sembra identico a √π

-1/2 ! = 1,7724538509055160272981674833411 = √π

Questo fa sì che anche la x in grado di risolvere l’equazione armonica che abbiamo visto poco sopra, in cui la x è un angolo vicinissimo a 60°, sia connessa con un’approssimazione di √π molto vicina al valore effettivo. E forse il lettore si ricorderà che anche dal doppio logaritmo di 360 avevamo ottenuto un’ottima approssimazione di √π

-cos 60°,003356468455..! = -0,49994926613916..! = 1,772277305.. ≈ √π = 1,772453850..

₂Ln 360 = 1,772594324.. ≈ √π = 1,772453850..

Ma, come abbiamo visto già a partire da The Snefru Code parte 3, dall’angolo di π/2 – il cui valore è connesso in modo del tutto ovvio da √π – possiamo ricavare dapprima un valore sperimentalmente possibile del numero caratteristico di ħ. Poi, da questo, un valore sperimentalmente possibile della costante di Planck h = 6,626

sen + cos + tg π/2 = 1,054458788.. ≈ ħ = 1,054571628..

tg x = ₃inv. Ln -1/1,054458788.. = ₃inv. Ln -0,948353800.. = 4,362797667..

x = 77°,09019315686377419238544439876

1/sinh 77°,090193.. = 1/1,509438771.. ∙ 10³³ = 6,62497889.. ∙ 10^-34 = h = 6,626

Dunque π si connette in modo perfetto o semiperfetto sia all’angolo giro sia a quello di 60° sia alla costante di Dirac. D’altra parte se prendiamo l’angolo che ha un seno iperbolico pari a π e lo trasformiamo numerologicamente in un seno iperbolico, l’angolo che a questo punto viene fuori è praticamente pari al numero caratteristico della costante di Boltzmann k = 1,38054 ∙ 10^-23 joule/K

tanh x = π; x = 1°,8622957433108482198883613251826

tanh y = 1,86229574..; y = 1,380300.. ≈ k = 1,38054

D’altra parte, se facciamo la potenza-specchio di 1,86229574.., noi vediamo che essa è praticamente pari a 10/π

1,86229574.. ^S = 3,183541037.. ≈ 10/π = 3,18309886.. (+4,421754.. ∙ 10^-4

In questo, come in molti altri casi, la differenza fra l’approssimazione e il numero esatto risulta matematicamente significativa, dato che pare connessa a un valore della costante di Planck che, di nuovo, rasenta la perfezione

4 + ⁸√(4,421754.. ∙ 10^-4) = 4 + ⁸√2261,545.. = 4 + 2,626036.. ≈ h = 6,626

9.

Dunque a questo punto abbiamo stabilito già una rete di relazioni che sembra già molto importante, ma che abbiamo lasciato in parte non analizzata per poter andare ancora avanti. Infatti, come oramai ci aspettiamo, anche quell’angolo particolare, il cui seno iperbolico è pari a 1/h, si porta dietro altre relazioni armoniche molto importanti. Infatti, se facciamo la doppia radice-specchio (ricordiamo al lettore che una radice specchio è la radice della forma ^x√x; però noi, per brevità, simbolizziamo la radice-specchio di un qualsiasi numero n con ^S√n; in caso che le radici formino una sequenza, aggiungiamo alla S dell’esponente il numero di volte consecutive che l’operazione va ripetuta: se va ripetuta, per esempio, 3 volte, scriveremo ^3s√n), scopriamo che essa è pari a sua volta a un’approssimazione di ħ

^2s√77°,090193156.. = 1,054717969.. ≈ ħ = 1,054571628..

Se adesso facciamo ₃inv. Ln -1/1,054717969.. arriviamo a un valore molto simile alla tangente dell’angolo di 77°,090193..

tg x = ₃inv. Ln -1/1,054717969.. = 4,3633779933363707101826527193703

x = 77,091852636.. ≈ 77°,090193..

Questo significa in primo luogo che l’angolo di 77°,090193.. è vicinissimo alla x in grado di soddisfare l’equazione armonica che vediamo qui sotto

^2s√x = -1/₃Ln tg x

x = 77°,091847030831533346232697817386

^2s√x = 1,0547170938022659080937893273263

D’altra parte, se noi trasformiamo numerologicamente tg 77°,0918470.. = 4,363376.. nell’angolo di 4°,363376.., noi vediamo che la tangente iperbolica di quest’angolo è a sua volta connessa con il valore della costante di Dirac che possiamo ricavare dal valore della costante di Planck che fu calcolato da Planck stesso all’inizio del secolo scorso

x = tg 77°,0918470.. = 4°,3633760326176228205879371946161

tanh 4°,363376.. = 0,99967567584369664260455101252269

(1/0,999675675..)¹²⁸ = 1,042394244.. ≈ ħ_Planck = 6,55/2π = = 1,042464877.. (-7,063279.. ∙ 10^-5

Inoltre, siccome la costante di Dirac risulta da quella di Planck divisa per 2π, è del tutto chiaro che l’angolo di 77°,090193.. – che, lo ricordiamo, abbiamo ricavato a partire dalla sommatoria di seno, coseno e tangente dell’angolo pari a π/2 – deve essere molto vicino alla x in grado di soddisfare l’equazione armonica che vediamo qui sotto

1/sinh x ∙ 10³⁴/(-1/₃Ln tg x) = 2π

x = 77°,090143056950877280610673063413

1/sinh x ∙ 10³⁴ = (6,625310809455499916015842879998 ∙ 10^-34) ∙ 10³⁴ = 6,625310809..

(-1/₃Ln tg x) = 1,0544509653..

6,625310809.. : 1,0544509653.. = 2π

Ma in The Snefru Code abbiamo visto che 2π è anche il limite a cui tende la funzione che vediamo qui di seguito

Lim_x→0 360°/(x/sen x) = 360°/57,295779513082320876798154814105 = 2π

Siamo partiti dall’angolo di 60° e finiamo con uno pari a 77°,090143.., connesso con la costante di Planck e quella di Dirac. Ma adesso scopriamo che valore molto vicino a quello dell’angolo 77°,090143.. lo si può ottenere da quello di 60° nel modo che vediamo qui di seguito

[(1 + sen 60°)²]^{(1 + sen 60°)²} = [(1 + sen 60°)]^S = 77°,036644972348655212215286766219

Il coseno di 60° lo si può ottenere, come abbiamo visto, dal logaritmo in base 10 di √10, e quindi dal 10. Ma abbiamo visto che dal valore negativo di √10 si può ottenere √π: esiste quindi una relazione perfettamente continua fra √10, il coseno di 60° e √π. Ma √10 si connette anche con il numero di Eulero, sia pure in modo imperfetto, attraverso il prodotto fattoriale

√(√10 !) = 2,71730432346662.. ≈ e = 2,718281828459045..

10.

Quindi, quello che sembrava un punto isolato, l’angolo di 60°, si è rivelato intimamente connesso con un nugolo di valori scientifici e matematici del massimo rilievo. Particolarmente importante sembra il fatto che dal logaritmo in base 10 di √10 si possa ottenere un valore di √π che sembra praticamente esatto. Le connessioni che potremmo descrivere sono naturalmente infinite. Ma in questo caso ci sembra giusto sottolinearne una semplicemente a causa della sua particolare stranezza, che proprio per questo può darci un’idea chiara del sistema in cui ci stiamo muovendo. Partiremo perciò dal quel numero la cui radice specchio (cioè ^x√x, che però di solito noi simbolizziamo, per comodità con ^S√x) è uguale al numero stesso diviso per 10, ovvero dalla x in grado di soddisfare l’equazione armonica che vediamo qui sotto

^x√x ∙ 10 = x = 12,267379049580302055971811315987

Applicando per 4 volte la funzione potenza-specchio alla x che abbiamo appena ottenuto divisa per 10 (un’operazione che corrisponde al ripetere per 4 volte sulla calcolatrice la funzione x^y partendo dal numero x: un’operazione che noi simbolizzeremo con 1,226737904..^4s), arriviamo a una discreta approssimazione di 2.

1,226737904..^4s = 2,0004890350441796503286114547937

Partendo dal suo valore negativo, possiamo arrivare a una discreta approssimazione di π facendo per 4 volte l’inverso del logaritmo naturale

₃inv. Ln -2,000489035.. = 3,141953.. ≈ π = 3,141592..

Oppure, possiamo arrivare ad approssimazioni di π anche partendo da numeri in cui il logaritmo naturale e quello a base 10 entrano in comunicazione. Per esempio, esiste un numero x di cui facendo, per 4 volte il logaritmo naturale, otteniamo il valore negativo di quello che otteniamo facendo per 2 volte il logaritmo in base 10

₄Ln x = ₂log x ∙ -1 = -0,4562213072084319..

x = 722,848162997096265..

Ebbene, se dividiamo questo numero per 2 e facciamo per 2 volte il logaritmo naturale, otteniamo di nuovo un’approssimazione di √π.

₂Ln 722,848162../2 = 1,773264.. ≈ √π = 1,772453..

Se invece facciamo per 2 volte il logaritmo naturale del numero così com’è, otteniamo un’approssimazione di (2/ɸ_Cheope)³. Possiamo quindi facilmente ricavarne un’approssimazione di 1/ɸ_Cheope nel modo che vediamo qui di seguito

³√₂Ln 722,848162.. : 2 = ³√1,884520.. : 2 = 1,235189.. : 2 = 0,617594.. ≈ 1/ɸ_Cheope = 0,617821..

Oppure, esiste un numero dal quale, facendo per 4 volte il logaritmo naturale oppure 3 volte il logaritmo in base 10, si ottiene lo stesso risultato. Se facciamo la radice specchio del risultato e poi il logaritmo in base 10, quella che otteniamo è di nuovo un’approssimazione di π

₄Ln x = ₃log x = -0,2131775081154..;

log ^S√-0,2131775081154.. = log 1408,720301.. = 3,148824.. ≈ π = 3,141592..

Anche in questo caso possiamo ricavare un’ottima approssimazione di ɸ_Cheope – 1 nel modo che vediamo qui di seguito

(1/inv. Ln -0,2131775081154..) : 2 = (1/0,808012..) : 2 = 1,237604.. : 2 = 0,618802.. ≈ ɸ_Cheope – 1 = 0,618590..

Situazioni di questo genere dunque ci fanno capire in quale strano labirinto matematico ci stiamo muovendo, e le ragioni per cui la sua esposizione risulta tanto difficile e tanto laboriosa. La forma del Tutto, in questo sistema, si confonde con la forma di ogni parte, e la forma di ogni parte con la forma del Tutto. Quasi che l’universo sia in realtà un grande specchio, che attraverso ogni immagine riflessa non fa altro che riflettere un sé stesso che continuamente sfugge nelle proprie immagini.

Capitolo 3:

LA CODIFICAZIONE DELLA COSTANTE DI DIRAC NEL CICLO DI SATURNO, VENERE E MERCURIO: UN PUNTO DI PARTENZA PER UNA SEQUENZA DI RELAZIONI ARMONICHE FRA CICLI COSMICI COSTANTI FISICHE E COSTANTI GEOMETRICHE

1.

Se quella sequenza armonica che abbiamo visto ci ha riempito di stupore, adesso dobbiamo prepararci a rinnovarlo, perché il punto di contatto fra i 2737 anni del ciclo di Saturno, Venere e Mercurio con quell’approssimazione della costante di Dirac che abbiamo definito poco sopra – corrispondente alla x in grado di soddisfare l’equazione armonica 2x = 1 + x/10 – lo possiamo stabilire in un modo non potrebbe essere più sorprendente. Iniziamo a scoprirlo nel momento in cui ci rendiamo conto che questi 2737 anni vanno a incastrarsi in modo quasi perfetto con la durata un altro ciclo lunare molto importante, oltre a quei due che abbiamo già visto. Le modalità di questo “incastro” hanno degli aspetti che appaiono davvero vertiginosi. Al punto che si arriva a domandarsi se Shakespeare, quando faceva dire ad Amleto «Ci sono più cose fra il cielo e la terra, Orazio, di quante ne sogni la nostra filosofia» si rendesse conto fino in fondo di quel che stava dicendo.

Comunque sia, ce ne renderemo conto noi, analizzando le connessioni fra il ciclo di Saturno, Venere e Mercurio e il cosiddetto “ciclo metonico”, che deve il suo nome all’Ateniese Metone, vissuto nel V secolo avanti Cristo, il quale notò che 235 mesi lunari coincidono con 19 anni solari. L’attribuzione di questa scoperta è diventata un po’ dubbia quando ci si è resi conto che il circolo megalitico di Callanish, fu costruito in modo tale che, proprio ogni 19 anni solari, la Luna andasse a tramontare proprio fra i pilastri centrali del circolo

Ma chi fra Metone e i costruttori di questo circolo megalitico che si affaccia sull’oceano abbia il primato della scoperta di questo ciclo cosmico, in questa sede ci interessa molto meno dei rapporti che esso sembra capace di instaurare con il ciclo di Saturno, Venere e Mercurio. Infatti, se facciamo il rapporto di questo ciclo con quello scoperto da Charles Marcello, otteniamo il 144, ovvero un numero fra i più importanti di quel “codice precessionale” che de Santillana e von Dechend hanno individuato nei miti cosmologici sparsi in tutto il mondo e in tutte le epoche

2737 : 19 = 144,052631578947368421052631578..

Il conto non è perfettamente pari, è vero. Però dobbiamo notare che anche in questo caso – proprio come in quello dei due valori di G che abbiamo dedotto da due equazioni armoniche – la differenza con il valore esatto sembra avere uno straordinario significato a livello matematico. Infatti, essa corrisponde esattamente a 1/19: ma la somma dei numeri che compongono il 2737 è proprio 2 + 7 + 3 + 7 = 19. Questo fatto crea un rapporto simbolico importantissimo non solo con il ciclo di Metone, ma anche con il sistema numerico Maya. Infatti i Maya , nella rappresentazione degli intervalli di tempo tra le date del loro calendario, usavano una notazione posizionale, con venti come base primaria e cinque come base ausiliaria e avevano un simbolo per ogni cifra da 0 a 19. Dal 19 possiamo inoltre ricavare un’ottima approssimazione di ɸ_Cheope e dunque anche della lunghezza di Planck nel modo che vediamo qui sotto

1 + (₂log 19! : 2) = 1 + (1,232617388.. : 2) = 1 + 0,616308694.. = 1,616308.. ≈ ℓ_P = 1,616252..

1/[1 + (₂log 19! : 2)] = 1/1,616308.. = 0,618693696.. ≈ ɸ_Cheope – 1 = 0,618590346..

E qui possiamo notare che se prendiamo un’approssimazione della lunghezza di Planck vicinissima al valore che abbiamo calcolato sopra, possiamo da essa derivare il valore della costante di Planck h = 6,626.. ∙ 10^-34 applicando la funzione sinh x per 5 volte. Quest’operazione corrisponde sulla calcolatrice a digitare un numero e pigiare per 5 volte consecutive il tasto “sinh”, e la simbolizzeremo perciò con ₅sinh

1/₅sinh (2/1,616340342241..) = 1/₅sinh 1,237363164014.. = 1/1,509204.. ∙ 10³³ = 6,626.. ∙ 10^-34 = h

Il 19 è anche la potenza che, con segno negativo, caratterizza la carica elettrica unitaria c_u = 1,6022 ∙ 10^-19. Questa costante è caratterizzata da uno stranissimo rapporto con il suo numero caratteristico, dato che se prendiamo l’approssimazione che vediamo sotto, gli togliamo 1, e poi applichiamo per 12 volte la funzione sinh x e andiamo a vedere l’inverso, scopriamo che si tratta ancora una volta dello stesso valore di c_u da cui siamo partiti, inclusa però questa volta la potenza del 10

1/₁₂sinh (1,60231533776.. – 1) = 1/1,60231533776.. ∙ 10^-19

Questo relazione vede al contempo ampliato e rafforzato il suo significato dal fatto che se facciamo l’inverso del numero caratteristico della costante che descrive l’unità della massa atomica, che viene definita come 1/12 della massa del Carbonio 12 ed è pari a circa 1,660538.. ∙ 10^-27 kg. Facendo in questo modo, quello che troviamo è ancora una volta il numero caratteristico della carica unitaria meno 1:

1/1,660538.. = 0,602214.. ≈ c_u – 1 = 0,6022

Una simile relazione circolare la scopriamo anche per la costante di Dirac ħ = 1,054571628 ∙ 10^-34 . Se prendiamo un’approssimazione come quella che vediamo qui sotto, la eleviamo alla quarta e e applichiamo .. volte la funzione sinh, facendo infine l’inverso ritroviamo il numero caratteristico da cui siamo partiti completo della potenza del 10

1/₅sinh 1,054894967..⁴ = 1/₅sinh 1,238331390.. = 1/9,479616747.. ∙ 10³³ = 1,054894967.. ∙ 10^-34

Incredibilmente, questo è anche il caso del raggio della prima orbita dell’elettrone 1bohr = 0,531 ∙ 10^-10, anche se in questo caso il rapporto fra i due capi delle funzioni è leggermente più complesso

₈inv. sinh 1/0,5309405.. ∙ 10^-10 = ₈inv. sinh 1,883450192.. ∙ 10^-10 = 0,883450192.. = 1/0,5309405.. – 1

2.

Le funzioni del seno iperbolico sembrano dunque confermare ancora una volta che la trigonometria a base 360° può essere considerata un sistema armonico, capace di mettere in relazione nei modi più imprevedibili che si possano immaginare i numeri più importanti della fisica e della matematica.

Per fare un esempio, in connessione con quanto abbiamo visto sembra notevole il fatto che partendo da un’approssimazione di c_u – 1 come quella che vediamo qui sotto si possa ricostruire il valore esatto del diametro classico del protone r_p = 1,535 ∙ 10^-18

1/₁₂sinh (1,601937211729359.. – 1) = 1/651465798045602605,863.. = r_p = 1,535 ∙ 10^-18

Né può sfuggire il fatto che questa particolare approssimazione di c_u – 1 può venir fuori a sua volta da un’approssimazione della costante di Planck h = 6,626 pari invece a 6,613028..

1/(1 + h/10) = 1/(6,613028../10) = 1/(1 + 0,6613028..) = 1/1,6613028.. = 0,601937211.. ≈ c_u – 1 = 0,6022

È interessante notare che quest’approssimazione di c_u – 1 segue dal logaritmo in base 10 di un numero intero sacro come il 4

log 4 = 0,602059.. ≈ c_u – 1 = 0,6022

Se adesso passiamo alla costante che descrive la massa dell’elettrone m_e = 9,109382 ∙ 10^-31 scopriamo che da essa possiamo ricavare un’approssimazione davvero buona di π/2 facendo per 4 l’inverso del seno iperbolico dell’inverso del valore della costante

₄inv. sinh 9,109 382 ∙ 10^-31 = ₄inv. sinh 1,097769310.. ∙ 10³⁰ = 1,570499.. ≈ π/2 = 1,570796..

A partire da una situazione come questa è facile gioco ipotizzare che altre funzioni di π e del seno iperbolico possano avere un significato matematico armonico e scientifico. E in effetti, anche su un piano immediato ci rendiamo conto che sia la tangente che il seno iperbolico dell’angolo pari a 1/π si connettono con valori molto significativi

sinh 1/π = 0,323712439.. ≈ 2ɸ_Cheope/10 = 0,323718069..

tanh 1/π = 0,307977.. ≈ d_p = 3,07

Invece, attraverso il seno iperbolico di c – 2 = 0,9979246 (che fra l’altro va vicinissimo al numero tipico del sarcofago di Djedefre, 1,17, che abbiamo analizzato in The Snefru Code parte 10), possiamo arrivare a una buona approssimazione della costante di Dirac

³√sinh 0,9979246 = ³√1,172001.. = 1,054328679.. ≈ ħ = 1,054571628..

Questi fatti ci spingono a pensare che anche attraverso il seno iperbolico sia possibile ritrovare quel complesso di relazioni armoniche legate a π, ɸ, il 10 e il numero di Eulero che abbiamo trovato attraverso le altre funzioni trigonometriche. Qui sotto vediamo una relazione circolare, in cui il numero di partenza ritorna su sé stesso dopo un percorso più o meno complicato. Stiamo parlando di quell’angolo il cui seno moltiplicato per il seno iperbolico da come risultato l’inverso della metà dell’angolo da cui siamo partiti. E qui di nuovo dobbiamo prendere atto delle infinite potenzialità armoniche dell’intorno numerico che ha come centro π, dato che la x in grado di soddisfare l’equazione armonica che vediamo qui sotto, è un numero vicinissimo a 2 + Ln π_Cheope

(sinh x ∙ sen x) = 1/(x : 2); x = 3,1451538704.. ≈ 2 + Ln π_Cheope = 3,145132304..

Lo stesso vale per il numero d’oro. Infatti, la x che sottratta al suo seno iperbolico ci dà come risultato la funzione esatta di ɸ che vediamo qui sotto, è a sua volta un numero vicinissimo a 1 + ɸ²

[sinh x] – x = 3 ∙ (ɸ + 1/ɸ)²; x = 3,61799628741.. ≈ 1 + ɸ² = 3,618033988749..

Simile a questa è l’equazione armonica che vediamo qui sotto, che viene soddisfatta da una x vicinissima al numero caratteristico della costante che descrive la massa del protone (m_p = 1,6725)

[sinh (2 + x)] – (2 + x) = 2³; x = 1,67304176.. ≈ 1,6725

3.

Analizzando infine le equazioni armoniche che vediamo qui sotto, ci rendiamo conto di quanto anche a livello del seno iperbolico π, ɸ, il 10 e il numero di Eulero siano strettamente legati fra di loro e, per esempio, con una costante importantissima come G, che in questo caso possiamo ottenere dal risultato a cui tende la seconda equazione armonica che vediamo qui sotto

sinh 2x = 360/π; x = 2,71727018.. ≈ e = 2,718281828..

1/(sinh π) ! ∙ 10⁹ = 6,473343189.. ≈ 4ɸ = 6,4721359549..

x : sinh x = e/10; x = 3,14267028045..;

1/(e/10) + c = 6,676719.. ≈ G = 6,672

Queste relazioni sembrano davvero molto interessanti, e sarebbe meglio esplorarle in modo più accurato di quanto, per ragioni di spazio e di continuità dell’analisi, non potremo fare in questa sede. Infatti, in questo modo ci accorgiamo di una complessa trama di relazioni che altrimenti ci sfuggirebbe del tutto. Prima di abbandonarle diamo un’occhiata all’ultima, che è anche la più stupefacente di tutte. La analizzeremo solo in parte, perché il complesso delle sue implicazioni e delle connessioni che da essa si sviluppano è talmente imponente che occuperebbe da solo tutto il resto dell’articolo.

Il punto di partenza è un numero un po’ particolare, ovvero il valore negativo dal quale, attraverso il prodotto fattoriale, possiamo ricavare 1 + Ln π, che è quello che vediamo qui sotto

-0,15208351163..! = 1,114472988584.. = 1 + Ln π

Come prima cosa, possiamo notare che se facciamo il logaritmo naturale del valore positivo di questo numero, troviamo dapprima una discreta approssimazione di -(2/ɸ_Cheope)³. Abbiamo dunque la possibilità di ricavare 1/ ɸ_Cheope nel modo che vediamo qui sotto

–³√Ln 0,15208351163.. : 2 = –³√-1,883325490.. = 1,234928446.. : 2 = 0,617464.. ≈ 1/ ɸ_Cheope = 0,617821..

Invece, facendo per due volte l’inverso del logaritmo, quel che troviamo è una discreta approssimazione del doppio della carica unitaria 2c_u = 3,2044. Similmente, facendo la radice quarta dell’inverso del numero, arriviamo nei pressi del valore di c_u = 1,6022

₂inv. Ln 0,15208351163.. = 3,203543.. ≈ 2c_u = 3,2044

⁴√1/0,15208351163.. = ⁴√6,575334757.. = 1,601324.. ≈ c_u = 1,6022

Dunque 0,15208351163.., questo numero dall’apparenza tanto anonima, ci permette di scoprire che il valore caratteristico della costante che descrive la carica elettrica unitaria, è connesso con la x in grado di soddisfare l’equazione armonica che vediamo qui sotto

1/[(₂inv. Ln x) : 2]⁴ = x = 0,15198420549.. ≈ -0,15208351163..

4.

Ma fin qui, potremmo dire, siamo ancora al livello delle banalità. Il piatto forte di quest’analisi deve ancora venire, e, come del resto ci aspettiamo, ci verrà servito proprio da delle funzioni del seno iperbolico. Infatti, se adesso prendiamo ancora una volta il valore positivo di questo numero e andiamo a vedere la tangente dell’angolo corrispondente, scopriamo che facendone l’inverso otteniamo una quasi perfetta approssimazione della costante di Planck h = 6,626. L’inverso del seno iperbolico corrisponde invece in modo praticamente perfetto alla costante di Planck nel valore che fu calcolato da Planck stesso all’inizio del secolo scorso h_Planck = 6,55

1/tanh 0°,15208351163.. = 1/0,15092172582.. = 6,625951.. ≈ h = 6,626

1/sinh 0°,15208351163.. = 1/0,15267045659.. = 6,55005.. ≈ h_Planck = 6,55

Il fatto che il coseno iperbolico di questo angolo sia pari a circa π/3 diventa persino un fatto banale, nel momento in cui ci rendiamo conto che i due valori della costante di Planck intrattengono un simile relazione nelle normali funzioni di trigonometriche di coseno e tangente. Infatti, se prendiamo un coseno pari ad h = 6,625951.. e ne facciamo l’inverso, trasformando numerologicamente il risultato in un coseno, vediamo che è il coseno di quell’angolo che ha per tangente quello stesso valore di h_Planck che abbiamo derivato per mezzo del seno iperbolico

cos x = tanh 0°,15208351163.. = 1/6,625951263.. = 0,15092172582..

x = 81°,319654314284574973462668068706

tg 81°,319.. = 6,55005.. ≈ h_Planck = 6,55

Che dire adesso quando scopriamo che questo numero tanto anonimo si lega a un’altra costante fisica legata al nome di Planck, ovvero alla lunghezza di Planck? In questo caso, la possiamo ottenere addirittura per due vie diverse, come possiamo constatare attraverso le equazioni che vediamo qui sotto

¹⁶√(1/0°,152082..)! = ¹⁶√6,575400..! = ¹⁶√2167,986046.. = 1,616231.. ≈ ℓ_P = 1,616252..

1 + ⁹√(1/0°,152082..)/2 = 1 + ⁹√6,57540../2 = 1 + 1,23276../2 = 1 + 0,616382.. = 1,616382.. ≈ ℓ_P = 1,616252..

Considerando che il coseno iperbolico di quest’angolo è pari a circa ⁴√π/3, attraverso di esso possiamo ricavare anche la costante di Dirac

(1/tanh 0°,152083511..) : (6 ∙ cosh⁴ 0°,15208351..) = 6,625951.. : 6,282958.. = 1,054590.. ≈ ħ = 1,054571..

E qui è bene concludere facendo notare che siamo partiti dal valore della x tale per cui -x! = 1 + Ln π/10, possiamo concludere che il termine ultimo dell’analisi può connettersi tanto a π che a ɸ per una via diversa da quella trigonometrica. Infatti, possiamo ottenere delle buone approssimazioni della costante di Dirac sia da π_Cheope = 22/7 e da ɸ attraverso un procedimento puramente matematico

^22/7√[(22/7)^22/7 – 22/7] – 2 = 1,054247592.. ≈ ħ = 1,054571628..

^{-(ɸᶲ – 2ɸ)}√-(ɸᶲ – 2ɸ) = ^{1,057610409..}√1,057610409.. = 1,054388451.. ≈ ħ = 1,054571628..

E qui possiamo sottolineare il fatto che dalla differenza fra i due valori di ħ che abbiamo appena ricavato possiamo ottenere un’ottima approssimazione di 1+ ℓ_P/10 = 1,1616252.. nel modo che vediamo qui sotto

⁹√log 1,054388451.. – 1,054247592.. = ⁹√log 0,000140858.. =

= ⁹√-3,851217.. = -1,1616263.. ≈ 1+ ℓ_P/10 = 1,1616252..

Oppure, possiamo di nuovo ottenerne una buona approssimazione di π, seguendo, per così dire, un moto matematico circolare, che con l’andare avanti nel lavoro ci diventerà sempre più familiare. In questo caso, come in molti altri abbiamo analizzato e che analizzeremo, anche il valore della differenza è matematicamente significativo, dato che corrisponde al numero caratteristico del diametro classico del protone moltiplicato per 10^-4

√(0,000140858..! – Ln 0,000140858..) = √[0,999918714.. – (-8,867756160..)] =

= √9,867674874.. = 3,141285.. ≈ π = 3,41592.. (-3,071087.. ∙ 10^-4 ≈ d_p ∙ 10^-4 = 3,07 ∙ 10^-4

5.

Lavorando con questa matematica antica si può aver spesso un senso di vertigine. Abbiamo messo in rapporto due cicli cosmici e abbiamo scoperto che da questo rapporto possiamo ricavare un numero sacro, con un resto un po’ particolare, pari a 1/19. Ma questa semplice operazione ci ha introdotto a una catena di relazioni e significati simbolici e numerologici davvero impressionante. Un ciclo planetario diviso per un ciclo solare/lunare, ed ecco che ci troviamo ad indagare intorno alle relazioni interne delle costanti della fisica per mezzo di funzioni del seno iperbolico: dei passaggi che, appunto, sembrano ancora più iperbolici che pindarici. Ma a giustificarli non è una fantasia sfrenata, ma bensì l’intrinseca struttura del sistema, in cui ogni parte si connette interminabilmente con il Tutto e attraverso il Tutto di nuovo con sé stessa.

Né possiamo dire di aver esaurito tutte le implicazioni del rapporto fra il ciclo di Saturno, Venere e Mercurio e quello di Metone. Infatti, il resto di 1/19, moltiplicato per 10³, è molto vicino alla radice c – 1 di 2737: il che sembra alludere a un’equazione armonica in senso stretto, ma a una generale proporzione del sistema. La sensazione è che, allontanandosi da un certo genere di rapporti armonici (in questo caso, quello fra il ciclo di Saturno, Venere e Mercurio e quello di Metone e le connessioni con altri valori importanti che abbiamo individuato: la matematica Maya, la potenza di 10 della costante della carica elettrica, etc.) non si va verso il caos, ma verso un altro genere di rapporti armonici, di cui però in ogni caso possiamo scorgere l’abbozzo

[(2737 : 19) – 144] ∙ 10³ = 1/19 ∙ 10³ = 52,631578.. ≈ ^{c – 1}√2737 = 52,531848..

E qui dobbiamo sottolineare il fatto che da (c – 1)/10² possiamo ottenere un’ottima approssimazione di π, dato che questa cifra si lega al seno di un angolo molto vicino a Ln π. Questa è solo una delle tante prove che nel corso del nostro lavoro abbiamo visto e che ancora vedremo, che il valore della velocità della luce, nell’ambito del complesso sistema armonico che è l’universo, non è da considerarsi un’entità fisica nel senso occidentale del termine, ma un’entità che contribuisce in modo decisivo alla costituzione della sua forma logico-matematica

sen x = (c – 1)/10² = 0,019979246

x = 1°,144802644.. ≈ Ln π = 1,144729885..

e^{1,144802644..} = 3,141821.. ≈ π = 3,141592..

Inoltre – e qui l’apparenza è quella di aver a che fare solo con una curiosità – se dividiamo l’angolo giro per 1/19 ∙ 10³ =, otteniamo un apparentemente anonimo 6,84

360 : 10³/19 = 360 : 52,631578.. = 6,84

Però questo numero, moltiplicato per 10², mostra di possedere un caratteristica un po’ strana, che vedremo comparire più volte in relazione a quell’indicibilmente e meravigliosamente complessa “armonia delle sfere” che fa sì che il nostro sistema solare sia ciò che è. Infatti il 684 è uno di quei numeri divisibili per 18 da cui, sommando le cifre che le compongono, si ottiene ancora una volta il 18

6,84 ∙ 10² = 684; 6 + 8 + 4 = 18; 684 : 18 = 38

Inoltre, come vedremo nel prossimo lavoro che pubblicheremo sul sito, 6,84 risulta dalla somma dell’altezza del gradino più alto della Piramide di Djoser con quella del gradino più basso (9,4 + 7,7 = 17,1) divisa per 10 e moltiplicata per 4

17,1/10 ∙ 4 = 1,71 ∙ 4 = 6,84

Di nuovo, la prima impressione senz’altro quella di avere a che fare con dei numeri qualsiasi. E invece avremo modo di vedere in un lavoro successivo le quasi incredibili caratteristiche matematiche di queste misure, apparentemente del tutto anonime e banali. E quando lo faremo, terremo a mente che le queste “misure miracolose” le avremmo anche potute derivare dal rapporto fra il ciclo di Saturno, Venere e Mercurio e il ciclo di Metone. Che però ci riserva altre sorprese, ancora maggiori di queste

6.

Infatti, solo ora arriviamo al punto che ci eravamo prefissi. Ovvero scoprire il rapporto fra il ciclo individuato da Charles Marcello e tutta quella complessa trama armonica di rapporti che abbiamo derivato a partire dall’analisi strutturale della costante G. Questo rapporto lo scopriamo nel momento in cui, moltiplicando per 10 il resto pari 1/19 del rapporto 2737/19, vediamo che il risultato corrisponde in modo assolutamente perfetto a quel numero che, moltiplicato per 2, ci da il numero stesso diviso per 10 con l’aggiunta di 1, ovvero alla x in grado di soddisfare l’equazione armonica 2 ∙ x = 1 + x/10. Il lettore ricorderà che questo è proprio quel numero che abbiamo sfiorato al termine dell’analisi delle relazioni armoniche fra la costante gravitazionale e il raggio della prima orbita dell’elettrone intorno al nucleo. In quel caso avevamo raggiunto questo valore

(2465,547616 – 2464,530421)³ = 1,0171946..³ = 1,0524760..

Invece, in questo caso, usando il resto della differenza fra il rapporto fra la durata del ciclo di Saturno, Venere e Mercurio e quello di Metone meno il numero sacro – [(2737 : 19) – 144] = 1/19 – noi troviamo il valore esatto della x in grado di soddisfare l’equazione armonica che abbiamo visto sopra

2 ∙ x = 1 + x/10;

x = [(2737 : 19) – 144] ∙ 10 = 1/19 ∙ 10 = 0,52631578947368421052631578..

2 ∙ 0,52631578947368421052631578.. = 1,052631578947368421052631578.. =

= 1 + (0,52631578947368421052631578.. /10) = 1,052631578947368421052631578..

Dato il contesto, sembra opportuno far notare che un numero molto vicino a 1 + 1/19 viene fuori anche dal prodotto fattoriale della frazione che possiamo ricavare dai due numeri del calendario Maya Haab’ 20/18

20/18 ! = 1,111111.. ! = 1,052183720.. ≈ 1 + 1/19 = 1,052631578..

L’assoluta straordinarietà di questa relazione viene confermata da un altro fatto importantissimo. Ovvero, che possiamo arrivare a un numero praticamente identico a 1,052631.. facendo 1/(tg – cos + sen 2737°). Si noti che il seno di 2737° è molto vicino al numero caratteristico della costante che definisce la carica elettrica unitaria (1,6022) meno 1, e che il valore della differenza con il numero esatto è una funzione piuttosto ben approssimata di √2

1/(tg – cos + sen 2737°) = 1/[0,753554050.. – (-0,798635510..) + (-0,601815023..)] =

= 1/0,950374536998.. = 1,052216743.. ≈ 1,052631578.. (-4,14835.. ∙ 10^-4 ≈ -(√2 – 1) ∙ 10^-3 = -4,14213.. ∙ 10^-3

Questa scoperta vede il suo significato ampliarsi ulteriormente perché il rapporto fra la lunghezza di Planck ℓ_P = 1,616252.. ∙ 10^-35 m e il raggio classico del protone r_p = 1,535 ∙ 10^-18 m corrisponde proprio a 20/19 = 1,052631578.. moltiplicato per 10^-17

ℓ_P/r_p = 1,616252.. ∙ 10^-35/1,535 ∙ 10^-18 = 1,052932.. ∙ 10^-17 ≈ 20/19 ∙ 10^-17 = 1,052631.. ∙ 10^-17

La piccola inesattezza che registriamo, pari a circa 3 decimillesimi, viene neutralizzata dal fatto che il principio di indeterminazione fa sì che in numeri caratteristici delle costanti della fisica debbano essere considerate non già dei punti sull’asse delle x, ma dei segmenti o, come degli intorni numerici. Dunque, se scegliamo dei valori di ℓ_P e di r_p leggermente diversi, ma ancora entro i margini consentiti dal principio di indeterminazione, ecco che la relazione risulta assolutamente perfetta

1,616199.. : 1,53538905.. = 20/19 = 1,0526315789473684210526315789474

Fra l’altro, questa approssimazione del raggio classico del protone è vicinissima alla x in grado di soddisfare le due equazioni armoniche che vediamo qui sotto

Ln 10^x = x + 2; x = 1,53540833.. ≈ r_p = 1,535

₂inv. Ln (log x) = 10/c = 3,33564092..; x = 1,535328777.. ≈ r_p = 1,535

Quindi, per l’ennesima volta, l’astronomia si è mostrata utile per la fisica in generale. Lo studio del ciclo individuato da Charles Marcello ci ha consentito di scoprire che anche il rapporto fra il raggio classico del protone e quello della lunghezza di Planck risulta da relazioni armoniche. E chi ha letto i lavori precedenti sa oramai che anche tutti gli altri parametri atomici che abbiamo analizzato possiedono a caratteristiche di questo genere. Dunque ci saremmo stupiti molto se questa avesse fatto in qualche modo eccezione, in specie se consideriamo che il numero il logaritmo in base 10 mesi lunari che è coinvolto nel ciclo di Metone (235) è vicinissimo alla x in grado di soddisfare l’equazione che vediamo qui sotto

log x + 2 = 10^x : 10² = x = 2,375812087593 ≈ log 235 = 2,371067862..

7.

Diciamo la verità: cose di questo genere sembrano sfidare la fantasia più sconvolta e sfrenata del più sfrenato e sconvolto dei romanzieri fantasy. La “lunga marcia matematica” che abbiamo fatto sembra dunque aver valso la pena, in specie se pensiamo che le meraviglie numerologiche connesse con il ciclo di Saturno, Venere e Mercurio non sono ancora finite.

Infatti, quest’indagine su un monumento che viene dall’antichità profonda dell’umanità, imprevedibilmente, ci riporta a un presente che, dal punto di vista matematico, è stato forse un po’ trascurato. Ci stiamo riferendo al fatto che un’approssimazione della x in grado di soddisfare l’equazione armonica 2 ∙ x = 1 + x/10 la possiamo ricavare anche dal modo in cui in Francia si denomina la settima decina dei numeri naturali. Come è noto, i Francesi non dicono una parola equivalente a “settanta” ma “soixante-dix”, cioè “sessanta-dieci”. In questo modo sembra che l’uso linguistico vada a sottolineare una relazione particolare fra questi due numeri – cioè il 60 e il 70. Una relazione che viene fuori quando facciamo la radice cubica del rapporto 70/60 e che ci consente di ottenere un’approssimazione della x in grado di risolvere l’equazione armonica 2 ∙ x = 1 + x/10 = 20/19.

³√(70 : 60) = ³√1,166666.. = 1,052726.. ≈ 1 + 1/19 = 1,052631.. (+9,502.. ∙ 10^-5 ≈ 1/(10/π)⁸ = 9,488.. ∙ 10^-5

Qualcosa di particolare viene fuori anche quando eleviamo la radice cubica di 70/60 alla 128sima potenza, e otteniamo così una buona approssimazione di (e – 2) ∙ 10³. Peraltro, anche il doppio del suo valore al quadrato contiene una buona approssimazione del numero di Eulero.

[³√(70 : 60)]¹²⁸ = 718,449683.. ≈ (e – 2) ∙ 10³ = 718,281828.. (+0,1678546718.. ≈ 1/6 + 1/29² = 0,167855727..

2 ∙ (70 : 60)² = 2 ∙ 1,166666..² = 2 ∙ 1,361111.. = 2,722222.. ≈ e = 2,7182818.. (+0,00394039..

La cosa più notevole sembra il fatto che in questo secondo caso l’inverso della differenza sia piuttosto vicino a (c – 1)⁸

⁸√1/0,003940393763176.. = ⁸√253,781743678.. = 1,9978254.. ≈ c- 1 = 1,9979246 (-0,0001..

La frazione (70 : 60)² = 1,361111.. sembra avere delle connessioni di tipo ermetico anche con la Luna. Infatti distanze estreme raggiunte dalla Luna durante la sua orbita sono rispettivamente 55,4 volte il raggio medio terrestre, la minima al perigeo e 66,1 volte la massima, all’apogeo. Ma dal punto di vista numerologico è interessante anche la distanza media, che corrisponde a circa 60,7 volte il raggio terrestre. Trasformando numerologicamente questo dato in un angolo di 60°,7, come vedremo in dettaglio più oltre, possiamo ottenere un’ottima approssimazione di π. Invece, la somma di seno e coseno risulta pari a 1,361117.. : una cifra davvero molto vicina a (70 : 60)² = 1,361111..

8.

Poco sopra siamo scivolati dall’infinitamente grande nell’infinitamente piccolo. Adesso siamo passati da quello che sembrava solo un modo di dire dei Francesi alla velocità della luce (ma più oltre vedremo quanto siano profonde le implicazioni storico-simboliche fra questo modo di esprimersi e il tema precipuo di questo articolo). Così, ci sembra giusto cogliere quest’occasione per sottolineare ancora una volta come il valore di c abbia delle caratteristiche matematico-armoniche davvero molto rimarchevoli. In questo caso, possiamo dare una rapida occhiata a cosa succede quanto lo elaboriamo con il prodotto fattoriale. Un lavoro che, in un momento successivo, andrà a connettersi con l’analisi della struttura di due di quei pianeti del sistema solare che fanno parte del ciclo individuato da Charles Marcello, vale a dire Mercurio e Venere.

Per cominciare, possiamo partire dall’osservazione che il prodotto fattoriale di 1 + c/10 ci dà un risultato davvero molto prossimo a 70/60. Il che ci fa sospettare ancor di più che questo modo di contare un po’ strano dei Francesi abbia dei fondamenti scientifici e matematici che risultano infine molto seri

(1 + c/10) ! = 1,29979246 ! = 1,166566634.. ≈ 70/60 = 1,166666.. (-0,0001..

Ma la caratteristica armonica più straordinaria della velocità della luce la possiamo scoprire facendo per 8 volte consecutive il prodotto fattoriale di (c – 1), usando un valore di c che si discosta da quello sperimentalmente stabilito di circa 5 milionesimi. Così facendo, quella che otteniamo non è nulla di meno che la radice di π. Per indicare il ripetersi consecutivo del prodotto fattoriale, scriveremo ₈!

(c – 1) ₈! = 1,997928503.. ₈! = 1,772453.. = √π

Né sembra meno importante il fatto che l’approssimazione di c che abbiamo usato sopra risulti praticamente identica a quello che, nei lavori scorsi, abbiamo ottenuto a partire da π e da ɸ e che possiamo rivedere qui sotto

π : [³²√(2ɸ + 2/ɸ)] = 3,141592.. : ³²√4,472135.. = 3,141592.. : 1,0479211.. = 2,997928556.. ≈ 2,997928503..

9.

Questa breve incursione sui numeri francesi ci dà inoltre l’occasione di introdurre un argomento che affronteremo poi in modo più preciso nella seconda parte di questo lavoro, ovvero la sezione aurea del 13, che si connette in modo evidente a quella sezione del semiciclo precessionale che troviamo a Giza (e un semiciclo precessionale dura appunto circa 13000 anni). Qui ci limitiamo a sottolineare il fatto che possiamo ottenerne un’ottima approssimazione facendo la radice quarta del prodotto di 70 per 60. Dato il contesto, non c’è da pensare che sia un caso che la radice quarta della differenza fra l’approssimazione e il valore esatto sia più o meno uguale alla durata dell’anno lunare (354,36 giorni) divisa per 10³

⁴√(70 ∙ 60) = ⁴√4200 = 8,050304.. ≈ 13/ɸ = 8,034441.. (+0,015862922..

⁴√0,01586292.. = 0,354891.. ≈ 354,36/10³ = 0,35436

L’approssimazione di ɸ che possiamo ricavare è pari a

13 : ⁴√4200 = 1,614845.. ≈ ɸ = 1,618033.. (-0,00318829508.. ≈ -1/10²π = 0,0031830988..

Dobbiamo sottolineare comunque, che il modo un po’ strano che hanno i francesi di definire il 70 sia connesso con dei significati matematici e scientifici non stupisce più di tanto. Infatti, tanto il 60, che il 10 che il 70 sono numeri sacri: e nei numeri sacri, presenti nei miti di tutto il mondo, come abbiamo avuto modo di vedere abbondantemente nei lavori precedenti, sono criptati in modo a volte neppure troppo arduo le conoscenze di una scienza ermetica di cui solo oggi cominciano a comprendere i connotati.

Capitolo 4:

UNA BREVE RETROSPETTIVA SUI FONDAMENTI GENERALI DELLE RELAZIONI MATEMATICHE INDIVIDUATE PER MEZZO DEL RAPPORTO FRA IL CICLO DI SATURNO, VENERE E MERCURIO E QUELLO DI METONE

1.

E qui, prima di proseguire oltre, sarà forse bene soffermarsi a fare un inciso per spiegare quali siano i fondamenti della strana relazione che abbiamo visto sopra fra il 19 e il 2737, dato che essa allude a una proprietà dei numeri naturali che, siccome appare del tutto ovvia e banale, mai o quasi mai viene presa in considerazione. In effetti, da questo punto di vista, si nota che il 2737 non ha proprio nulla di straordinario, dato che tutti i numeri da cui sommando i componenti possiamo ottenere 19 (per esempio, 847; 8 + 4 + 7 = 19; 6571; 6 + 5 + 7 + 1 = 19; etc.) se divisi per 19 danno un numero intero più una frazione il cui denominatore è sempre 19, anche se non è sempre 1/19, come nel caso del 2737

25822 : 19 = 1359,0526315789473684210526315789 = 1359 + 1/19

26821 : 19 = 1411,6315789473684210526315789474 = 1411 + 12/19

375211 : 19 = 19747,947368421052631578947368421 = 19747 + 18/19

469 : 19 = 24,684210526315789473684210526316 = 24 + 13/19

Questa però, come subito si nota, non è una caratteristica particolare dei numeri che come somma danno 19, ma invece è una caratteristica generale di tutte le divisioni fra numeri interi. Se prendiamo un numero qualsiasi e lo dividiamo per un numero intero qualsiasi – risulti o no dalla somma dei suoi componenti – il risultato è sempre e comunque un altro numero intero più una frazione, il cui denominatore è costituito dal divisore. Se prendiamo il caso del 656 – tanto per prendere un esempio qualsiasi – sia che lo dividiamo per la somma dei suoi costituenti, che per qualsiasi altro numero, il risultato è sempre un numero intero più una frazione con denominatore pari al divisore

656

6 + 5 + 6 = 17;

656 : 17 = 38,588235294117647058823529411765 = 38 + 10/17

656 : 28 = 23,428571428571428571428571428571 = 23 + 12/28

656 : 36 = 18,222222.. = 18 + 8/36

Dunque, quello che abbiamo riscontrato per mezzo del ciclo di Saturno, Venere e Mercurio è un fatto matematico che, pur avendo un’apparenza che sul momento può apparire straordinaria, per altro verso risulta il caso particolare, pur con dei connotati molto strani, di una regola universale. Perché dunque soffermarsi su di esso addirittura con un intero capitolo del nostro lavoro?

2.

Rendersi conto di quella che, in ultima analisi, risulta una banalità, ovvero che qualsiasi numero si può dividere per la somma dei numeri di cui è composto, potrebbe per altro verso avere una certa importanza. Infatti, una relazione del genere sembra disvelare qualcosa che potremmo definire come una struttura nascosta che lega la serie dei numeri naturali. È vero, noi possiamo esprimere qualsiasi rapporto fra numeri interi con un numero intero più una frazione. Ma, se invece di dividere un numero intero in modo arbitrario lo dividiamo per la somma dei suoi componenti, quella che cogliamo non sembra più una banalità, ma un aspetto importante del rapporto che il numero intrattiene con quella che potrebbe risultare infine una parte essenziale della sua struttura.

Noi possiamo dividere, per esempio, il 2737, anche per 13: però il 13 non sembra avere nulla a che fare con la struttura del numero: nulla di più del 12 o del 48, etc. Dunque, il rapporto che troviamo non pare organicamente contenuto nel numero, ma invece del tutto estraneo ad esso. Invece, il rapporto fra il 2737 e il 19 sembra qualcosa di quasi naturalmente connesso al numero. Lo stesso vale per il 294, che è il prodotto di 2 ∙ 7 ∙ 3 ∙ 7, o per la frazione 2/147, che è l’inverso di 2 : 7 : 3 : 7.

E questo sembra valere anche per altri rapporti, che paiono intrinsecamente connessi con quella che potremmo definire come l’intima struttura aritmetica del numero.

Infatti, se scindiamo il 2737 nei suoi componenti, ecco che possiamo dividere le migliaia di cui è composto (cioè 2000) per la somma delle centinaia, delle decine e delle unità di cui è composto (cioè per 737). Anche in questo caso il 2737 rivela una particolarità di rilievo, perché così facendo ci troviamo piuttosto vicini al numero di Eulero

2000 : 737 = 2,713704.. ≈ e = 2,718281.. (-0,0457..

Oppure, se dividiamo la somma delle migliaia e delle centinaia (cioè 2700) per quella delle decine e delle unità (cioè per 37), ci troviamo di nuovo di fronte all’approssimazione a un numero sacro, il 72

2700 : 37 = 72,972972..

Quindi, se analizziamo la sua struttura, il 2737 non ci pare più un numero così qualsiasi come potrebbe sembrare a prima vista. Anche se facciamo astrazione da quelle connessioni con altri numeri che a vario titolo possiamo definire “speciali”, rimane il fatto che in questo modo possiamo distinguerlo – per esempio – dal numero naturale che immediatamente lo precede in modo ben più complesso e articolato di come siamo abituati per solito.

Relazioni di questo genere diventano ancora più interessanti quando ci rendiamo conto che esse comprendono ovviamente anche i numeri primi. Seguendo questa linea di pensiero, essi potrebbero essere definiti da una funzione di tre numeri, la cui scelta però non dipenderebbe dal caso, ma, come abbiamo detto, dalle parti costitutive del numero stesso. Per esempio, il 349 sarebbe definito da

16 ∙ (21 + 13/16) = 349

La definizione di questo numero, come presumibilmente anche quella di quasi tutti gli altri numeri primi, è a sua volta composta in parte da numeri primi, in parte da numeri non primi. Ma ovviamente, potremmo definire tanto il 16 che il 21 in base ai loro fattori primi, arrivando in questo modo a definire anche i numeri primi in base a numeri primi, diciamo così, più fondamentali.

Per esempio, il 17, seguendo questa formula, sarebbe 17 = 8 ∙ (2 + 1/8). Riducendo 8 ai suoi fattori primi abbiamo che 17 = 2³ ∙ (2 + 1/2³). Il 13 sarebbe definito ugualmente per mezzo del 3 e del 2 come 2² ∙ (3 + 1/2²). Ovviamente, nel caso in cui trovassimo delle potenze che non sono fattori primi, potremmo scomporre anche quelle nei loro fattori primi. Una procedura di questo genere ci consentirebbe forse di trovare dei denominatori comuni di tipo diverso da quelli a cui siamo abituati.

3.

Ci sono invece, come abbiamo detto, dei numeri primi che non avrebbero bisogno di questa operazione, perché già, diciamo così, al primo colpo risultano costituiti da altri numeri primi. Facciamo l’esempio del 331 perché, come vedremo ben presto, questo numero primo sembra avere un interesse scientifico di un certo rilievo. Se lo definiamo nel modo che abbiamo detto, vediamo che esso viene

331 = 7 ∙ (47 + 2/7)

Dicevamo che questo è un numero di particolare interesse scientifico perché appare legato alla costante di Planck h in modo abbastanza diretto. Se prendiamo un’approssimazione, peraltro abbastanza comune, pari a 6,62 ∙ 10^-34 e la scriviamo 662 ∙ 10^-36, allora il suo numero caratteristico corrisponderebbe a 2 ∙ 7 ∙ (47 + 2/7). In altre parole, fra le tante caratteristiche particolari di questo numero, potremmo annoverare anche il fatto che esso segue da un numero primo – il 331 – che è funzione solo e soltanto di altri numeri primi.

Questo a tutta prima può parere un caso. E chissà, forse lo è davvero. Ma, certo, abbiamo ben visto in molti lavori precedenti come h abbia delle carrateristiche che paiono straordinariamente rilevanti. A quanto pare, la Mente Divina, nel dare una struttura matematica all’universo, in nessun punto si è messa a tirare i dadi, pur se il determinismo con cui abbiamo a che fare non sembra in nulla simile a quello a cui ci ha abituati la meccanica classica.

Abbiamo visto sopra nel caso della costante gravitazionale che persino i resti delle operazioni non sono degli scarti, ma si rapportano in modo diretto ad altre grandezze fisiche e matematiche significative. Ma un tal genere di connessioni si è rivelato anche nell’analisi dei 2737 anni del ciclo di Saturno, Venere e Mercurio. Quando lo abbiamo diviso per il ciclo di Metone, la cui durata corrisponde alla somma dei suoi costituenti, abbiamo ottenuto un numero sacro. Ma ora ci apprestiamo a scoprire che una cosa del genere, vale anche per la costante di Planck. E, in maniera ancora più radicale, vale anche per le misure della Piramide, le cui intrinseche strutture numeriche hanno degli aspetti che definire sconvolgenti è dire poco. Ma, prima di arrivare a quel punto, è bene soffermarsi un attimo sulla costante di Planck.

Come primo esempio, possiamo notare che se si moltiplicano i costituenti del numero caratteristico di h = 6,626 considerandoli come numeri interi otteniamo

6 ∙ 6 ∙ 2 ∙ 6 = 432 = 3 ∙ 144

In modo un po’ sorprendente, ecco che scopriamo un legame insospettabile fra la costante di Planck e un numero sacro, onnipresente in tutta l’antichità. E questo sembra davvero un fatto nuovo. Fino ad adesso ci siamo stupiti di trovare la nostra cultura scientifica codificata in un oggetto antico come la Grande Piramide. Adesso ci stupiamo di trovare un pezzo di cultura antica, uno dei numeri più importanti del codice astronomico sacro, codificato in una delle nostre costanti più fondamentali. E possiamo anche notare che, almeno su un piano numerologico, questa relazione si lega anche con il problema posto dal quell’angolo che vediamo rappresentato nella figura qui sotto. Infatti, se dividiamo 432 per 10⁴, in questo modo andiamo a trovare un’ottima approssimazione (che forse potremmo anche definire un’idealizzazione) della differenza fra l’angolo che nella figura sottostante è stato ricavato da ɸ e quello che è stato ricavato da π.

Il cerchio si chiude quando ci rendiamo conto che da quell’angolo ε = 0,043109843 che vediamo in figura, possiamo ricavare un’ottima approssimazione della costante di Planck, da cui abbiamo dedotto in modo numerologico un’approssimazione di quell’angolo. Il che ci conferma per l’ennesima volta il radicale legame matematico fra le costanti delle fisica e π e ɸ, che abbiamo mille volte dimostrato nei lavori passati

10^0,043109843 ∙ 6 = 1,104357901934.. ∙ 6 = 6,626147.. ≈ h = 6,626

4.

Ma, tornando al nostro argomento, se consideriamo anche l’aspetto decimale delle cifre di cui si compone la costante di Planck (6 ∙ 6/10 ∙ 2/100 ∙ 6/1000 = 0,000432) e poi facciamo la radice di 432 usando 0,000432 come esponente – facendo infine la radice 2¹⁵ del risultato quello che otteniamo è una buona approssimazione del numero caratteristico della costante che descrive il raggio classico del protone r_p = 1,535

^2¹⁵√(^0,000432√432) = 1,535243513.. ≈ r_p = 1,535

Ma l’inverso di 0,000432 ha anche un significato autonomo, dato corrisponde al seno iperbolico di un angolo il cui coseno è molto vicino a π_Cheope²/10

sinh x = 1/0,000432; x = 8°,4402321969361058364973511861115

cos 8°,440232.. = 0,989169511.. ≈ π_Cheope²/10 = 9,877551020..

Se invece sottraiamo a π_Cheope² il valore del coseno di 8°,440232.. otteniamo un valore interessante, perché, diciamo così, ha una discreta somiglianza di famiglia con quello ricavato da Miquel Pérez Sanchez dalle misure della Piramide

π_Cheope² – cos 8°,440232.. = 8,888381508..

Il lettore si sarà accorto che procedendo in questo modo, l’immagine che abbiamo della matematica e dei numeri cambia completamente. Anche i numeri naturali non ci appaiono più come una serie di entità legate da un succedersi piatto e senza qualità, dei punti inestesi la cui definizione è un nome costituito di segni che infine non significano nulla di più del posto che occupano nella successione. Analizzato a questo livello, il 2737del del ciclo di Saturno, Venere e Mercurio si rivela pieno di significati e di legami strutturali con altri numeri. Ma, come abbiamo visto, lo stesso vale per la costante di Planck e, presumibilmente, anche per altre costanti.

5.

In effetti, anche la costante di Newton (G = 6,672) possiede almeno in parte queste stesse caratteristiche interne un po’ speciali, oltre a tutte le altre che abbiamo analizzato nelle parti precedenti di questo lavoro. In questo caso, se facciamo l’inverso del prodotto del numero intero per i decimali (6 ∙ 6/10 ∙ 7/100 ∙ 2/1000 = 0,000504), scopriamo che si tratta di un numero molto vicino alla stessa costante G elevata alla quarta potenza, mentre la radice quarta dell’inverso della differenza è praticamente pari a 5, cioè a (ɸ + 1/ɸ)²

⁴√1/0,000504 = ⁴√1984,126984.. = 6,674094.. ≈ G = 6,672 (+0,001594719..

⁴√1/0,001594719.. = ⁴√627,069705.. = 5,004134..

Si noti anche che la radice nona di 1/0,000504 è vicinissima a quel numero la cui radice cubica è uguale al numero stesso meno 1, ovvero alla x in grado di soddisfare l’equazione armonica che vediamo qui sotto

³√x = x – 1 = 1,3247179572447460259609088544781

x = 2,3247179572447460259609088544781 ≈ ⁹√1/0,000504 = ⁹√1984,126984.. = 2,324858938..

Il valore di G che possiamo ricavare dalla x in grado di soddisfare l’equazione armonica qui sopra collima con i valori massimi del numero caratteristico della costante che si possono trovare andando un po’ in giro su internet.

⁴√(2,324717957244..)⁹ = 6,6731841290179258419536826873334

A un livello numerologico, dobbiamo notare anche il fatto, che sembra piuttosto notevole, che togliendo a quest’approssimazione di G le prime tre cifre e moltiplicandolo per 10² otteniamo anche un’ottima approssimazione di 1/π. Che è più o meno quel che accade quando facciamo la stessa cosa con 2/π.

(6,673184129017.. – 6,67) ∙ 10² = 0,3184129017.. ≈ 1/π = 0,318309886..

(2π – 6,28) ∙ 10² = 0,3185307179586476925.. ≈ 1/π = 0,318309886..

Il caso di 2π sembra piuttosto interessante perché se procediamo allo stesso modo con latri segmenti della sua parte decimale, si vanno scoprire approssimazioni di numeri interessanti. Una cosa questa che può anche far pensare che non ci troviamo di fronte a una casualità

(2π – 6,28318530) ∙ 10⁶ = 0,7179586476925.. ≈ e – 2 = 0,7182818.. ≈ 1/³√e = 0,716531..

(2π – 6,28318530717958) ∙ 10¹³ = 6,476925.. ≈ 4ɸ_Cheope = 6,474361384

Fatti come questi sembrano indicare che è possibile concepire il numero non più come un punto come un asse cartesiano, ma come una complicatissima struttura di cui fa parte a pieno titolo anche la sequenza dei numeri con cui viene rappresentato, per esempio, per mezzo di un intero e di decimali. E vedremo poco più oltre quali possano essere le importantissime conseguenze teoriche di questa diversa concezione del numero.

6.

Ma, continuando l’analisi della struttura del numero caratteristico della costante gravitazionale, possiamo notare che dalla radice 32sima di 10 elevato alla G = 6,672 si può ricavare il numero caratteristico della lunghezza di Planck (ℓ_P = 1,616256..), una misura che, come avevamo previsto all’inizio di questo lavoro, essendo connessa con ɸ_Cheope sembra destinata a saltar fuori un po’ dappertutto. Un valore molto simile a ℓ_P lo possiamo ottenere anche da 10 elevato alla h = 6,626

³²√10^6,672 = 1,616218.. ≈ ℓ_P = 1,616256..

³√10^6,626/10² = 1,616838.. ≈ ℓ_P = 1,616256..

E qui sembra notevole anche il fatto che dall’approssimazione della lunghezza di Planck che ricaviamo da ³√10^6,626/10² possiamo ricavare un angolo vicinissimo a quello che ha per seno iperbolico 360/ɸ² semplicemente aggiungendo 4

sinh x = 360/ɸ² = 137,50776408942480085174509201215

x = 5,616840783.. ≈ 4 + ³√10^6,626/10² = 5,616838591.. (-2,191.. ∙ 10^-6

Dunque, da quel che possiamo vedere, i numeri che costituiscono l’ossatura della fisica, lungi dall’esser dei punti qualsiasi su di un asse cartesiano, un’accozzaglia di segni che stanno lì perché il caso ce li ha messi, fanno invece parte di una struttura organica, intelligente, che ritroviamo anche nella struttura interna al numero stesso.

In effetti, se procediamo con altre costanti allo stesso modo in cui abbiamo fatto con G e con h vediamo che questo strano “miracolo matematico” tende a ripetersi: dunque, in un certo senso, non si tratta di un miracolo, ma di una legge stabile che definisce la natura di certi numeri. Una legge di cui fino ad adesso non avevamo avuto il sentore.

Per esempio, procedendo in questo modo con 1bohr = 5,3 – ovvero con il numero caratteristico che descrive il raggio della prima orbita dell’elettrone attorno al nucleo – che, come abbiamo visto sopra, tanto strettamente si connette al valore di G – possiamo ricavare un valore vicinissimo a quello dell’approssimazione di π che fu codificato nella Grande Piramide π_Cheope = 22/7. Un fatto ancor più significativo quando ci ricordiamo che dallo stesso valore diviso per 10 si può dedurre parimenti un’approssimazione quasi perfetta di ɸ_Cheope. Il che significa, letteralmente, che per mezzo del raggio della prima orbita si potrebbero ricostruire in modo quasi perfetto le proporzioni fondamentali della Grande Piramide: ci basterebbe alterare il valore di 1bohr di che abbiamo scelto di una frazione e il gioco sarebbe fatto

²⁷√10^{1bohr = 5,3} = 1,571434.. ≈ π_Cheope/2 = 1,571428..

³√1/1bohr : 2 = ³√1/0,53 : 2 = ³√1,886792.. : 2 = 1,235685.. : 2 = 0,617842.. ≈ 1/ɸ_Cheope = 0,617821..

Il valore del numero caratteristico della massa dell’elettrone – che sul piano scientifico è connesso con il raggio della sua orbita – è invece molto strettamente legato a una funzione di ɸ_Cheope = 1,618590346..

log [₃inv. Ln (⁹√ɸ_Cheope)²] = log 1285867127,382063.. = 9,1091960.. ≈ m_e = 9,1091

E qui conviene notare che la radice m_e = 9,1091 di ɸ_Cheope corrisponde a una buona approssimazione della costante di Dirac

^9,1091√ɸ_Cheope = ^9,1091√1,61850346.. = 1,054287658.. ≈ ħ = 1,054571628..

E qui possiamo notare di passaggio che dalla massa e dal raggio classico del protone possiamo ricavare un’approssimazione praticamente perfetta di ɸ_Cheope nel modo che vediamo qui sotto

³√[m_p + (m_p ∙ r_p)] = ³√[1,6725 + (1,6275 ∙ 1,535)] = ³√(1,6725 + 2,5672875) =

³√4,2397875 = 1,61850742.. ≈ ɸ_Cheope = 1,61850346..

Dando un’occhiata all’equazione qui sopra possiamo dedurre che un valore molto prossimo a m_p ∙ r_p possiamo ricavarlo da 5/2 + (m_p – 1)/10. E, ricordandoci che 5 può essere immaginato come (ɸ + 1/ɸ)², ci rendiamo conto di quanto sia profonda e intricata la relazione del numero d’oro con il sistema della fisica.

[5/2 + (m_p – 1)/10] : m_p = (2,5 + 0,6725/10) : 1,6725 = 2,56725 : 1,6725 = 1,534977.. ≈ r_p = 1,535

Vedendo cose come queste viene quasi da pensare: il mondo intero non è altro che un gigantesco e complicatissimo frattale. Come abbiamo fatto fino ad ora a non rendercene conto?

7.

Beh, qualcuno potrà dire: non ce ne siamo accorti perché le cose non stanno così. Alla fine, tutti questi calcoli che stiamo facendo possono anche sembrare molto astratti, e la teoria che stiamo portando avanti appare forse, diciamo così, troppo teorica, per poter avere qualcosa a che fare con la realtà. Però questi dubbi rischiano si essere molto superficiali, perché, se andiamo a vedere le strutture di alcuni legami chimici molto comuni, ecco che ci rendiamo conto che le indagini che stiamo conducendo potrebbero avere infine anche dei risvolti molto ma molto concreti.

Nel 1957 i chimici R. Nyholm e R. Gillespie misero a punto una teoria che permetteva di prevedere la geometria delle molecole. Tale teoria fu chiamata VSEPR, acronimo della denominazione inglese Valence Shell Electron Pair Repulsion cioè repulsione tra doppietti elettronici del guscio di valenza. Secondo tale teoria le coppie di elettroni più esterne, avendo tutte la stessa carica negativa, tendono a respingersi le une con le altre e a disporsi il più lontano possibile.

Molecole con quattro legami e nessun doppietto solitario sull’atomo centrale assumono geometria tetraedrica con i legami disposti a 109,5° l’uno dall’altro. Il metano presenta una struttura di tal genere, che può essere rappresentata con legami a cuneo:

Se adesso andiamo ad analizzare le caratteristiche trigonometriche di questa struttura chimica, vediamo che esse hanno profondamente a che fare con il tipo di strutture geometriche matematiche che stiamo indagando. L’angolo con un coseno pari a -1/c è praticamente identico a questo che vediamo qui sotto dato che

cos x = -1/c = -1/2,9979246 = -0,333564092..

x = 109°,485244816.. ≈ 109°,5

Dal seno invece possiamo ricavare una discreta approssimazione del valore della carica unitaria

(1/sen 109°,485244..)⁸ = (1/0,942727..)⁸ = 1,060751..⁸ = 1,602916.. ≈ c_u = 1,6022

Inoltre, se dividiamo l’angolo giro per 109°,5, vediamo che il risultato che otteniamo è del tutto anonimo e insignificante solo in apparenza. Esso infatti va molto vicino a quel numero che, sommato al suo doppio logaritmo in base 10, è uguale a 3

x + ₂log x = 3; x = 3,286709950922.. ≈ 360° : 109°,5 = 3,28767123287.. (9,612.. ∙ 10^-4

Questo fatto ci spinge a notare che (3 + 360°/109°,5)/2 ci dà a sua volta una discreta approssimazione di π

(3 + 360°/109°,5)/2 = (3 + 3,28767123) : 2 = 3,143835.. ≈ π_Cheope = 22/7 = 3,142857..

E, se prima abbiamo immaginato che il mondo non sia altro che un gigantesco frattale, adesso ci viene spontaneo proseguire quel percorso di pensiero ricordando i cinque elementi di cui parlava Platone nel Timeo

Fino ad ora abbiamo pensato a quel dialogo come a una raccolta di ingenuità prescientifiche. Ma non potrebbe darsi che il suo contenuto alludesse in modo ermetico a una chimica – chissà – magari molto più avanzata della nostra? In The Snefru Code parte 8 abbiamo mostrato le prove che ad Alatri si sono costruite le mura poligonali riducendo la pietra calcarea allo stato liquido. Non può darsi che della chimica platonica facesse parte il segreto di questo modo di trasformare la materia, che a noi resta a tutt’ora completamente sconosciuto?

8.

Derivata da quella tetraedrica (verrebbe voglia di scrivere: da quella platonica) è la geometria piramidale, che caratterizza molecole con tre legami e una coppia di elettroni solitaria sull’atomo centrale. A causa della maggior repulsione della coppia solitaria sulle coppie di legame, l’angolo di legame risulta essere inferiore a 109,5°.

Presenta questa geometria la molecola dell’ammoniaca nella quale gli angoli di legame sono di 107,3°:

Anche l’angolo di 107°,3 risulta congruente con il tipo di rapporti armonici che stiamo analizzando. Esso infatti è caratterizzato da un coseno pari a circa 1/(π/3): ma chi abbia letto The Snefru Code parte 9 ricorderà che la lunghezza del lato Est-Ovest della Camera del Re espressa in metri è giusto pari a circa 10π/3 = 10,471..

(1/sen 107°,3) ∙ 3 = 1,047382.. ∙ 3 = 3,142148.. ≈ π_Cheope = 3,142857..

Invece il coseno di 107°,3 si va a connettere al numero caratteristico della massa del protone m_p = 1,6725, perché il suo inverso moltiplicato per 2 equivale in modo praticamente esatto a (m_p – 1) ∙ 10. Sul momento questa può sembrare una connessione un po’ forzata, se non proprio cervellotica. Ma andando avanti nel lavoro prenderemo coscienza sempre di più che in questo sistema i numeri non vanno intesi come punti sull’asse delle x, ma come sequenze di costituenti semplici. In questo modo, anche le porzioni di numeri significativi assumono un significato pari o a volte ancora maggiore di quello del numero nel suo complesso. E questo sembra proprio il caso della – chiamiamola così – desinenza decimale del numero caratteristico della massa del protone, che coincide praticamente con quello della costante gravitazionale

(1/cos 107°,3) ∙ 2 = 6,725517.. ≈ (m_p – 1) ∙ 10 = 6,725

La tangente di questo angolo invece ha una caratteristica armonica molto strana, dato che se facciamo per 3 il logaritmo naturale, otteniamo un valore vicinissimo alla sua radice-specchio. In pratica essa è molto vicina a quella x in grado di risolvere l’equazione armonica che vediamo qui sotto

-(₃Ln x)^S = x = 3,21240866.. ≈ -tg 107°,3 = 3,210630361.. (0,0017785.. ≈ ⁴√10/10³ = 0,001778279..

Vi sono poi molecole con due legami e due coppie di elettroni solitarie sull’atomo centrale che assumono una geometria angolata, anch’essa derivata dalla geometria tetraedrica. Le due coppie solitarie occupano due vertici del tetraedro ed esercitando una forte repulsione nei confronti degli elettroni di legame, comprimono l’angolo di legame a valori inferiori rispetto a quelli caratteristici della geometria piramidale.

Presenta questa geometria la molecola dell’acqua H₂O nella quale gli angoli di legame sono di 104,5°

Sulla molecola dell’acqua abbiamo già presentato un’analisi molto complessa in The Snefru Code parte 12 (che è anche la prima parte de “La Matematica Divina”). Rimandiamo dunque il lettore a quel testo. Però qui possiamo aggiungere a quanto già scritto allora che l’angolo di 104,5 ha una tangente pari a

-3,86671309.. ≈ -(3 + sen 60°) = 3,866025403.. = 3 + √3/2

L’angolo con la tangente pari a -(3 + sen 60°) differisce da quello di 104,5 di un’inezia. Dunque, tenendo conto dell’approssimazione con cui vengono misurati questi valori, possiamo senz’altro considerarlo come uno dei valori sperimentalmente possibili dell’angolo caratteristico della struttura di questo tipo particolare di molecole

tg x = -(3 + sen 60°); x = 104,502470516.. ≈ 104°,5 (+0,00247..

Dividendo l’angolo giro per mezzo di questo angolo possiamo ottenere un’ottima approssimazione di ɸ_Cheope

√(360 : 104°,5) : 3 = √3,444976.. : 3 = 1,856064 : 3 = 0,618688.. ≈ ɸ_Cheope – 1 = 0,618590.. (9,787.. ∙ 10^-5

9.

Dunque, contrariamente a quel che abbiamo fermamente creduto nel ventesimo secolo, sembra proprio che in natura niente di niente sia lasciato al caso. Al contrario, da quel che abbiamo visto nelle pagine precedenti, come peraltro anche nei precedenti articoli, sembra prender sostanza un’idea di Keplero, che la modernità ha relegato da secoli nel novero delle romantiche superstizioni: ovvero che numeri come ɸ e π non sono numeri qualsiasi, ma parte essenziale della Mente Divina. È attraverso questi numeri che l’universo è stato creato come un musicista crea un’armonia. O, meglio: come un complesso sistema di armonie. Infatti, i numeri che costituiscono la struttura nascosta dell’universo si connettono fra di loro in tutti i modi possibili immaginabili e, certe volte, diciamo così, anche in modi che a prima vista sembrano impossibili e inimmaginabili. Ciò fa sì che entro questa struttura, ogni parte rimanda all’altra, meravigliosamente, interminabilmente, in un continuo ed elegante contrappuntare.

Questo ci spinge a pensare che davvero, dal dividere un numero per la somma dei numeri che lo costituiscono, o da procedimenti similari, può risultare una ricerca molto importante. Noi fino ad ora, quanto a procedimenti di questo tipo, utilizziamo in pratica soltanto i prodotto fattoriale, che è l’unico che abbiamo profondamente a che fare con i componenti del numero (c’è anche un’operazione come la ricerca del minimo comun denominatore o del minimo comune multiplo, ma anche queste sono operazioni che pratichiamo in modo piuttosto occasionale). Quanto al resto, noi abbiamo la tendenza a vedere i numeri come punti inestesi e restiamo del tutto indifferenti alla loro reale o almeno possibile articolazione interna.

Ma sembra davvero il caso di superare questa autolimitazione, perché nei procedimenti che abbiamo sperimentato sia pure in modo tanto provvisorio ed embrionale in questo capitolo, sembra annidarsi un mondo di relazioni rimaste finora nascoste. Un mondo che pare abbracciare ogni sorta di entità matematica. Anche se prendiamo la costante di Planck nel valore calcolato da Planck stesso all’inizio del secolo scorso, h_Planck = 6,55, e facciamo il prodotto della parte intera per quella decimale, secondo il metodo che abbiamo utilizzato sopra, ci troviamo immediatamente di fronte alla più inaspettata delle sorprese. Infatti, quello che otteniamo è l’inverso di un altro numero sacro, ovvero il Numero della Bestia, e, davvero, viene spontaneo domandarsi: che cosa ci fa l’Apocalisse di San Giovanni Apostolo nel numero che ha inaugurato l’era della fisica atomica e del principio di indeterminazione?

1/(6 ∙ 5/10 ∙ 5/100) = 1/0,15 = 6,666666..

E qui possiamo notare che ci basta dividere questo risultato per 10², ed ecco che abbiamo ottenuto un angolo che ha per seno iperbolico la costante gravitazionale divisa a sua volta per 10²

x = 1/15 = 0,066666..; sinh 0°,066666 = 0,06671606.. ≈ G/10² = 0,06672

Se seguiamo un procedimento di scomposizione e ricomposizione del numero simile a quello che abbiamo usato con h_Planck con il numero d’oro fino alla quinta cifra, saltando ovviamente lo 0, otteniamo il 144 ∙ 10^-11. Se arriviamo fino alla sesta otteniamo quello stesso 432 che abbiamo ottenuto dalla costante di Planck, solo moltiplicato per 10^-17. E di nuovo mondi storici e branche del sapere che sembravano divisi da abissi di tempo e da diversità ideologiche insanabili, incredibilmente, sembrano toccarsi

1 ∙ 6/10 ∙ 1/10² ∙ 8/10³ ∙ 3/10⁵ = 144 ∙ 10^-11

1 ∙ 6/10 ∙ 1/10² ∙ 8/10³ ∙ 3/10⁵ ∙ 3 ∙10⁶ = 432 ∙ 10^-17

Difficilmente possiamo immaginare una situazione teoreticamente più sconcertante. L’analisi della struttura interna del numero ci porta a scoprire legami insospettabile fra ɸ e h, che per di più passano per uno dei numeri più importanti del codice astronomico sacro: il 144. Fra l’altro, procedendo oltre nella moltiplicazione verso decimali sempre più piccoli, quello che per forza di cose andiamo a scoprire è un legame inestricabile di ɸ e di h con il 144. Infatti, ovviamente, andando avanti a moltiplicare il 144 altro non facciamo che trovare multipli del 144.

Se poi facciamo la medesima operazione con π, ben presto ci troviamo di fronte a un altro numero sacro, il 54, anch’esso un multiplo del 18.

3 ∙ 1/10 ∙ 4/10² ∙ 1/10³ ∙ 5/10⁴ ∙ 9/10⁵ = 54 ∙ 10^-15

Nel caso della costante gravitazionale (6,672) e del Numero della Bestia (666), vediamo che il 36 che risulta dal prodotto delle prime due cifre è a sua volta un multiplo del 18. Dunque questo numero, che fu uno dei più sacri per i Maya, è una sorta di strano minimo comune divisore di h, G, π, ɸ e del Numero della Bestia.

10.

Sembra dunque che procedure di questo genere ci diano modo di scoprire una trama di relazioni che appaiono davvero molto interessanti, la cui estensione in questo momento non siamo in grado di immaginare. Esse sembrano rivelarci che numeri come π hanno un senso matematico profondo non solo se riferite al cerchio, ma, per esempio, anche se ci volgiamo all’interna sequenza dei loro componenti.

Anche se ci volgiamo alle ricerche “controcorrente” che abbiamo svolto fino ad adesso, dobbiamo riconoscere che, prima facie, potevano sembrare aprioristicamente qualcosa di piuttosto ridicolo. Chi sarebbe mai stato disposto ad immaginare che vi fossero dei legami tanto profondi, per esempio, tra il numero di Eulero, ɸ e π, o che dal numero di Eulero si potesse ottenere l’inclinazione espressa in gradi e sessantesimi di grado della Grande Piramide. E invece questo è quel che ancora una volta vediamo qui sotto

¹¹√[1/(e – 2)]¹⁶ = 1,618175531.. ≈ ɸ = 1,618033988..

[(e – 2)² – (e – 2)/10³] ∙ 10² = 51,52.. ≈ 51°51′

₃inv. Ln (³√e – e) = ₃inv. Ln -2,001750517.. = 3,14134050.. ≈ π = 3,14159265..

Anche quanto al senso matematico di quelle che abbiamo chiamato “equazioni armoniche” si potevano aprioristicamente nutrire dubbi, peraltro comprensibilissimi. Poi però ci rendiamo conto che il numero di Eulero può essere considerato un’approssimazione dell’equazione armonica che vediamo qui sotto

[1/(x – 2)]³ = x = 2,7166701878.. ≈ e = 2,718281828459.. (-0,00157994973570274120261216549611

Che un accostamento di questo genere possa avere un senso profondo, sia a livello scientifico che matematico, ce lo dimostra il fatto che dalla differenza che abbiamo registrato, sopra possiamo ricavare per mezzo dell’inverso del logaritmo in base 10, la tangente della sezione aurea dell’angolo giro. A sua volta, l’inverso della differenza con il valore esatto si rivela come il numero caratteristico del raggio classico del protone moltiplicato per 10³

₂inv. log -0,001579949.. – 9 = 0,916733463940.. ≈ tg 360°/ɸ = 0,91608191550.. (+6,51548439.. ∙ 10^-4

1/6,51548439.. ∙ 10^-4 = 1534,805.. ≈ r_p ∙ 10³ = 1,535

Questa “forma armonica” della matematica che viene fuori dalle nostre indagini ci spinge a pensare che possa riguardare anche la struttura profonda dei numeri. Ed è per questo che pensiamo sia conveniente dedicare un po’ delle nostre energie intellettuali a un’indagine tanto innovativa e perciò tanto affascinante e tanto promettente.

Per fare un altro esempio, qui sotto possiamo vedere un altro numero costituito da dei componenti la cui somma è 19, come nel caso del 2737. E anche in questo caso troviamo una discreta approssimazione del numero di Eulero, che poi scopriamo avere delle relazioni con ɸ_Cheope: un fatto come questo potrebbe farci un giorno scoprire un particolare legame fra il numero di Eulero e il 19

748 : 19 = 39 + 7/19 = 39 + 1/2,714285.. ≈ 39 + 1/e

748 – [(39 + 1/e) ∙ 19] = -0,010290617..

[₂inv. log -0,010290617.. ) – 3] : 4 = (9,475093.. – 3) : 4 = 1,618773.. ≈ ɸ_Cheope = 1,618590..

Quest’approssimazione del numero di Eulero ha inoltre, altre particolarità che sembrano ancor più interessanti. Facendo per 2 volte consecutive l’inverso del logaritmo naturale della differenza con il valore effettivo di e = 2,718281.. otteniamo questo numero che vediamo sotto, che è molto vicino a 2 + 1/(√c – 1)

2,714285714285 – 2,718281828459.. = -0,00399611417333094964600175706696

₂inv. Ln -0,003996114.. = 2,707462527.. ≈ 2 + 1/(√c – 1) = 2,707473949..,

In effetti, tutto il nostro lavoro risulta fondato solo se sono fondate le procedure matematiche innovative che usiamo per portarlo avanti. Se procediamo con esse, possiamo dire che con le equazioni che abbiamo appena visto troviamo dunque l’ennesima conferma che niente nell’universo è fatto caso, che ogni sua parte è armonicamente connessa con il Tutto e il Tutto con ogni sua parte. Se invece le rifiutiamo, e rifiutiamo la visione del numero che in esse è implicita, tutto il nostro lavoro parrà semplicemente un modo, magari originale e interessante, di produrre nonsensi. Scopo del capitolo successivo è perciò quello di dimostrare in un modo più soddisfacente possibile, se non la verità, almeno la plausibilità delle nostre ipotesi, che, volendo, possiamo sintetizzare dicendo che la struttura generale del mondo dei numeri è qualcosa che si può trovare anche in ogni singolo numero, dato che ogni singolo numero è a sua volta costituito di numeri.

Il nostro ragionamento sembra in questo momento allontanarsi da quello che è l’oggetto dichiarato della presente ricerca: l’analisi del Plateau di Giza in quanto meridiana precessionale. Ma se il lettore prosegue con fiducia nella lettura, vedrà che lentamente tutti i fili di questo ragionamento si riuniranno in una trama tanto esteticamente splendida, quanto logicamente convincente.

Capitolo 5:

UN TENTATIVO DI APPLICAZIONE DELL’ANALISI STRUTTURALE DEL NUMERO ALLE MISURE DELLA GRANDE PIRAMIDE E ALLE RELAZIONI FRA LA DURATA DELL’ANNO SOLARE E DI QUELLO LUNARE

1.

E qui possiamo finalmente cogliere in pieno l’utilità delle considerazioni matematiche che abbiamo appena svolto in relazione all’argomento di questo articolo. Perché, in effetti, il segreto delle straordinarie caratteristiche armoniche delle misure della Piramide espresse in cubiti (lato 440, altezza 280), sembra proprio stare nelle proporzioni interne che i componenti del 440 e del 280 stabiliscono fra di loro e al loro stesso interno. Ovvero non solo a livello dei rapporti fra i numeri intesi come punti su di un asse cartesiano, ma anche fra quelli che – come potremmo dire – rappresentano la loro intima struttura numerologica. In altre parole sembra che numeri come il 440 e il 280 siano qualcosa come un composto organico – e dunque animato – di costituenti più semplici: un po’ come il corpo rispetto alle cellule che lo compongono e come la cellula rispetto alle molecole e agli atomi su cui è fondata. In questo senso, noi potremmo dire che la Piramide, costituita com’è da questi rapporti, abbia qualcosa di più di una struttura. Invero, già il suo apparire, al tempo stesso imponente e armonioso, ha suggerito a molti che essa possieda qualcosa come un’anima: un’anima che risulta dalla matematica sul cui fondamento è stata costruita.

Per chiarire immediatamente ciò di cui stiamo parlando, analizzando questi numeri subito si nota che se facciamo il prodotto dei costituenti di 440 e 280 (ovviamente escludendo lo 0) otteniamo in entrambi i casi 16, dato che 4 ∙ 4 = 16, e 2 ∙ 8 = 16. Oppure, se li dividiamo per la somma dei loro numeri costitutivi otteniamo dei numeri diversi, è vero: ma sommando i loro componenti arriviamo in entrambi i casi a 10, come possiamo vedere qui sotto

440 : 8 = 55; 5 + 5 = 10

280 : 10 = 28 8 + 2 = 10

Oppure, moltiplicando le centinaia per le decine, arriviamo in entrambi i casi a 16000.

400 ∙ 40 = 16000

200 ∙ 80 = 16000

Facendo la divisione delle centinaia e delle decine che compaiono nei due numeri, arriviamo in entrambi i casi a 2. Facendo la divisione “incrociata” arriviamo in entrambi i casi a 5

400 : 200 = 2

80 : 40 = 2

400 : 80 = 5

200 : 40 = 5

Sommando i primi due risultati che abbiamo ottenuto, arriviamo a 2 + 2 = 4. Ma 4 è anche il risultato della divisione fra i prodotti incrociati delle decine e delle centinaia.

(400 ∙ 80) : (200 ∙ 40) = 32000 : 8000 = 4

Inoltre, la somma di 32000 + 8000 = 40000 = 4 ∙ 10⁴. Se facciamo il prodotto numerologico dei numeri coinvolti nell’espressione del 40000 per mezzo della potenza del 10, arriviamo a 4 ∙ 4 ∙ 10 = 160, ovvero a 10 volte il prodotto dei costituenti dei due numeri (infatti, come abbiamo visto, 4 ∙ 4 = 16 e 2 ∙ 8 = 16). Naturalmente, 160 è anche alla differenza fra il lato e l’altezza della Piramide, 440 – 280 = 160

(400 ∙ 80) + (200 ∙ 40) = 32000 + 8000 = 40000 = 4 ∙ 10⁴

4 ∙ 10 ∙ 4 = (400 ∙ 40) : 100 = (200 ∙ 80) : 100 = 440 – 280 = 160

Da ciò possiamo infine dedurre che il lato e l’altezza della Piramide si possono ottenere sommando e sottraendo 80 al numero dei giorni “puri” di un anno solare Antico Egizio o Maya, che è lo stesso dei gradi di un angolo giro

360 + 80 = 440

360 – 80 = 280

2.

A tutto ciò dobbiamo aggiungere il fatto che in The Snefru Code parte 3 abbiamo scoperto che, per esempio, le misure del lato e dell’altezza della Grande Piramide contengono codificati tanto il numero di Eulero, che ɸ e il 10 e che, per mezzo dei resti, vi è codificato anche π. Quanto all’altezza, pari a 280 cubiti, possiamo vedere che essa si può derivare con approssimazione straordinariamente buona dal numero di Eulero e da ɸ nel modo che vediamo qui sotto

(e ∙ 103) + ³√{[3 + (2/ɸ)³] : 10⁶} =

= 279,98302833128165924210960954932 + 0,01697174524528906140854666576538 =

= 280,00000007652694830351815621509 ≈ 280

La radice nona dell’inverso della differenza è molto vicina a 10/ɸ_Cheope

⁹√1/0,00000007652694830351815621509 = 6,175715621.. ≈ 10/ɸ_Cheope = 6,17821552..

Quanto al lato, senza stare a ripetere le lunghe analisi cha abbiamo svolto in quella sede, ci sembra giusto però rivedere il modo geniale in cui questi numeri compaiono nel 440. In primo luogo, possiamo notare che 440 è particolarmente vicino a 10^π : π = 441,004..; questo significa che possiamo ottenerlo a partire dal 10 e da un numero molto vicino a π, che è quello che vediamo qui di seguito

10^{3,1404436866..} : 3,1404436866.. = 440

E questo è già un avvertimento che 440, anche se in un primo momento sembra solo, diciamo così, un composto del numero di Eulero, del 10 e di ɸ, deve avere qualcosa a che fare con π. È una cosa di cui ci renderemo conto lavorando sul piccolo resto che noi, ragionando in stile occidentale moderno, saremmo indotti a trascurare, attribuendolo come al solito al caso.

(440 : e) : 10² = (440 : 2,718281828..) : 100 = 161,86695411543462150203045887104 : 100 =

= 1,6186695411543462150203045887104 ≈ ɸ (+6,3555240445136681571775434476188 ∙ 10^-4

Se adesso però prendiamo il valore della differenza escludendo la potenza del 10 (in pratica, moltiplicandolo per 10⁴, cioè per una funzione del 10, un altro numero codificato nel lato) e facciamo il prodotto fattoriale e lo dividiamo per 10³, ecco che ci troviamo davanti a una sorpresa

6,355524..! : 10³ = 1,414601766.. ≈ √2 = 1,414213562.. (+3,88203990.. 10^-4

Se adesso prendiamo eleviamo al quadrato quest’approssimazione di √2, vediamo che dal suo valore negativo viene fuori un’ottima approssimazione di π

₃inv. Ln -(1,414601766..)² = ₃inv. Ln -2,001098157.. = 3,141657545.. ≈ π = 3,141592653.. (6,489.. ∙ 10^-5

Potremmo andare avanti con l’analisi, e scoprire così molteplici connessioni. Ma ne mostriamo solo una in cui questa differenza che abbiamo appena trovato va a connettersi con una funzione trigonometrica.

sen x = ⁸√(6,489153379.. ∙ 10^-5) = 0,299587373..

x = 72°,567178511..

tg 72°,567178511.. = 3,184609747.. ≈ 10/π = 3,183098861. (+0,0015108853894535537299135211117

L’inverso di questa differenza corrisponde ancora una volta a un multiplo di un’approssimazione di ɸ.

1/0,001510885389.. = 661,863571506024.. ≈ (5 + ɸ_Cheope) ∙ 10² = 661,8590346..

A questo punto, quel che abbiamo visto probabilmente è sufficiente per arrivare alla conclusione, che secondo noi non può essere che questa: che numeri come il 440 – e in sé stessi ma anche e soprattutto rapportati con un numero come il 280 – non furono considerati dai costruttori della Piramide come dei punti inestesi sull’asse cartesiano. Essi vennero pensati invece come delle complicatissime strutture matematiche, il termine di una gran quantità di rapporti armonici di ogni sorta, attraverso cui sono legati umano, a tutti gli altri numeri. Il numero infatti non era per loro una successione meccanica di simboli insignificanti, ma bensì un qualcosa di simile a una rete neuronale, la base di ogni corretto pensare, l’immagine dell’Intelligenza Divina. Ma siccome l’universo non è altro che una proiezione dell’Intelligenza Divina nella realtà sensibile attraverso i numeri, ecco che noi, quando ci guardiamo intorno, senza esserne coscienti vediamo la Mente Divina mentre pensa.

3.

Questo fatto, che sul momento sembrerà a molti solo un’immagine mitica, ci apparirà come qualcosa di molto più serio nel momento in cui ci ricordiamo che in The Snefru Code parte 13 avevamo visto che le proporzioni dello stesso genere che abbiamo or ora analizzato – ovvero le proporzioni interne, strutturali, fra il lato e l’altezza della Grande Piramide – riguardano anche la durata dell’anno solare (365,25) e quella dell’anno lunare (354,36): due cicli astronomici che nel passato sono stati vissuti come un sovrapporsi di differenti tempi cosmici, che ci si è dati molto da fare per conciliare. Conviene rivedere queste relazioni strutturali anche in questa sede, per l’ovvia parentela che mostra, per esempio, con le misure in cubiti della Piramide: ci renderemo in questo modo conto di come e da dove hanno imparato le loro tecniche gli architetti Antico Egizi.

Come primo passo della nostra analisi, possiamo notare che il rapporto fra la durata dell’anno solare e di quello lunare, moltiplicato per 6, è pari a circa 10 ∙ (ɸ_Cheope – 1). Una proporzione molto simile a quella che risulta da 2ɸ/π

(365,25 : 354,36) ∙ 6 = 1,030731459.. ∙ 6 = 6,18438875.. ≈ (ɸ_Cheope – 1) ∙ 10 = 0,618590346..

(2ɸ/π) ∙ 6 = 1,030072429600.. ∙ 6 = 6,18043457.. ≈ 1/ɸ ∙ 10 = 6,18033988..

Ma, come spesso succede in questi casi, quando il rapporto fra due numeri risulta significativo, risulta significativo anche il prodotto. Qui, in primo luogo, possiamo notare che la radice del prodotto di 365,25 per 354,36 è quasi identica alla somma dei due numeri divisa per 2. In secondo luogo, tanto il prodotto che la somma della durata dell’anno solare e di quello lunare ci consentono di ottenere in modo semplice e diretto un’ottima approssimazione di √π

₂Ln √(365,25 ∙ 354,36) = √129429,99 = ₂Ln 359,763797.. = 1,772482.. ≈ √π = 1,772453..

₂Ln [365,25 + 354,36) : 2]} = ₂Ln 359,805) = 1,772502.. ≈ √π = 1,772453..

E qui possiamo notare che anche dal Numero della Bestia, cioè con il 6 periodico, possiamo ricavare un’approssimazione straordinariamente buona di √π. In questo modo, comprendiamo che uno dei fondamenti della sua sacralità non è altro che nella sua relazione profonda con il ciclo lunare e quello solare

1 + ⁶⁴√2/3 ∙ 10⁷ = 1 + ⁶⁴√0,000000666.. = 1 + 0,772455.. = 1,772455.. ≈ √π = 1,772453..

4.

Dunque, quelle che i nostri matematici considererebbero solo delle coincidenze banali, o delle curiosità, esprimono un’armonia talmente meravigliosa da fare impallidire il genio di Bach. Infatti, quel che abbiamo visto fino ad adesso non altro che il prologo di relazioni che, a dispetto della possibilità di essere riprodotte con il calcolo, non cessano perciò di apparire come una specie di strano, infinitamente ripetibile miracolo.

Possiamo cominciare osservando che se sommiamo la parte intera di 365,25 e 354,36 alla rispettiva parte decimale, viene sempre fuori lo stesso numero, il 390: questo numero è anche il risultato del rapporto fra la somma delle migliaia, delle centinaia e delle decine che compongono il numero degli anni del ciclo di Saturno, Venere e Mercurio (2730) – con le sue unità (7)

365 + 25 = 390; 354 + 36 = 390; 2730 : 7 = 390

Se poi sommiamo i componenti di questo numero otteniamo 9 + 3 + 0 = 12, il numero di mesi dell’anno solare e lunare. Ma il 12 è lo stesso numero che troviamo se facciamo il rapporto fra quella che potremmo definire la “divisione sequenziale” dei numeri che compongono il 365,25 e il 354,36 e lo moltiplichiamo poi per 10. Lo stesso succede se invertiamo l’ordine della divisione.

1/[(3 : 6 : 5 : 2 : 5) : (3 : 5 : 4 : 3 : 6)] ∙ 10 = 1/[1/100 : 1/120] ∙ 10 = 1,2 ∙ 10 = 12

1/[(5 : 2 : 5 : 6 : 3) : (6 : 3 : 4 : 5 : 3)] ∙ 10 = 1/(1/36 : 1/30) ∙ 10 = 1,2 ∙ 10 = 12

Il lettore avrà notato senz’altro un fatto molto importante: che moltiplicando i denominatori delle frazioni che abbiamo ottenuto dalle due divisioni sequenziali del 365,25 e del 354,36 si ottiene in entrambi i casi 3600, ovvero il numero dei giorni “puri” dell’anno solare Antico Egizio e Maya e i gradi dell’angolo giro moltiplicati per 10: infatti

36 ∙ 100 = 3600

30 ∙ 120 = 3600.

Un altro rapporto simmetrico lo possiamo individuare nel fatto che

36/120 = 30/100 = 3/10.

Inoltre, possiamo ottenere il 12 in maniera molto simile facendo il rapporto fra i prodotti delle centinaia, delle decine, delle unità, dei decimi e dei centesimi di 354,36 e 365,25, come possiamo vedere qui sotto

[(300 ∙ 50 ∙ 4 ∙ 3/10 ∙ 6/100) : (300 ∙ 60 ∙ 5 ∙ 2/10 ∙ 5/100)] ∙ 10 = (1080 : 900) ∙ 10 = 1,2 ∙ 10 = 12

Il 365,25 si caratterizza anche per il fatto che dalla divisione sequenziale di centinaia, decine, unità, decimi e centesimi otteniamo 100 e che procedendo in modo opposto e facendo l’inverso del risultato otteniamo 36000. Dividendo 36000 per 100 otteniamo 360: il numero di giorni “puri” del calendario solare Antico Egizio e Maya, oltre ai gradi dell’angolo giro

300 : 60 : 5 : 2/10 : 5/100 = 100

1/(5/100 : 2/10 : 5 : 60 : 300) = 1/2,777777.. ∙ 10^-6 = 360000

36000 : 100 = 360

Se poi facciamo il prodotto della divisione sequenziale delle centinaia, delle decine e delle unità con quello dei decimi e dei centesimi, otteniamo 4. Un numero sacro in tutte le culture, ovunque simbolo dei punti cardinali, e dunque dello spazio, e molto spesso anche delle stagioni. Se invece di fare il prodotto facciamo la somma otteniamo il 5 e dalla differenza otteniamo il 3. Abbiamo così ottenuto la terna pitagorica sacra 3, 4, 5, che è alla base delle proporzioni della Piramide di Chefren

(360 : 60 : 5) ∙ (2/10 : 5/10²) = 1 ∙ 4 = 4

(360 : 60 : 5) + (2/10 : 5/10²) = 1 + 4 = 5

(2/10 : 5/10²) – (360 : 60 : 5) = 4 – 1 = 3

5.

Ma dobbiamo però notare che queste strutture matematiche sono ancora più complesse di quanto non abbiamo visto fino ad ora. Infatti, se dividiamo la parte intera di 365,25 per la parte decimale, troviamo uno dei due numeri con cui gli Antichi Egizi simbolizzavano il ciclo di Sirio, vale a dire il 1460.

365 : 0,25 = 1460

Invece, se moltiplichiamo la somma delle centinaia e delle decine per le unità (300 + 60 = 360), per i decimi e per i centesimi, otteniamo il 18, ovvero il numero di periodi di 20 giorni con cui i Maya dividevano i giorni puri del calendario solare Haab’, che erano 360 (gli Antichi Egizi invece, com’è noto, li dividevano in 12 parti di 30 giorni ciascuna).

360 ∙ 5 ∙ 2/10 ∙ 5/100 = 18

Se sommiamo i componenti del 1460 e del 18, otteniamo 20, ovvero la durata del singolo periodo del calendario Maya Haab’. Se dividiamo 1460 per 20, otteniamo un altro numero appartenente al codice sacro individuato da de Santillana e von Dechend, il 73

1 + 4 + 6 + 1 + 8 = 20

1460 : 20 = 73

Già a questo punto possiamo notare che almeno 4 costrutti umani, vale a dire il triangolo sacro con lati 3, 4, 5, la Piramide di Chefren, il calendario solare Maya e quello Antico Egizio, sono contenuti nella struttura matematica di due fenomeni naturali quali la durata dell’anno solare e di quello delle fasi lunari. E, a sua volta, il triangolo sacro 3, 4, 5, contiene in sé degli “sviluppi numerologici” che fino ad adesso non sono stati mai analizzati, ma che sembrano davvero molto significativi.

Infatti, noi possiamo intendere il triangolo 5, 4, 3 come una sequenza che definisce due numeri, il 345 e il 543. Se facciamo il prodotto di questi due numeri e poi per 3 volte il logaritmo in base 10 otteniamo un’ottima approssimazione di -√2/10

₃log (543 ∙ 345) = ₃log 187335 = -0,141446932267.. ≈ -√2/10 = -0,141421356237..

Da questo numero possiamo facilmente ricavare un’approssimazione di 2 e poi da questa, secondo uno schema che abbiamo già visto, un’approssimazione di π che differisce dal numero esatto di circa 2 decimillesimi

inv. Ln -(-0,141446932 ∙ 10)² = inv. Ln -2,000723464.. = 3,141839.. ≈ π = 3,141592..

Se invece facciamo il rapporto 543/345, vediamo che il numero che viene fuori, senza bisogno di alcuna elaborazione è piuttosto vicino a π/2: l’approssimazione di π che possiamo ricavarne differisce dal valore esatto di poco più di 6 millesimi

(543 : 345) ∙ 2 = 1,573913043.. ∙ 2 = 3,147826.. ≈ π = 3,141592

Ma 543 e 345 sembrano assumere significato anche se presi in considerazione isolati. In particolare, se prendiamo il 543 e facciamo per 3 volte il logaritmo in base 10 troviamo un’approssimazione davvero buona di 360/10³. Un’approssimazione che si connette a sua volta a π in modo ancora più esatto, di nuovo secondo uno schema che oramai dovrebbe esserci diventato familiare. Impressiona profondamente il fatto che dividendo la durata dell’anno solare e facendo il logaritmo naturale, si ottiene in pratica lo stesso risultato che facendo per 3 volte il logaritmo in base 10 di 543. In questo modo, la durata dell’anno solare diventa qualcosa come un trait d’union fra π l’angolo giro e i due tipi di logaritmi, e dunque anche fra il numero di Eulero e il 10, attraverso la mediazione del triangolo sacro 3, 4, 5

₃log 543 = -0,359592564.. ≈ -(Ln 365,25/10) = 0,359799695..

₂Ln -0,359592564.. ∙ -10³ = ₂Ln 359,592564.. = 1,772401.. ≈ √π = 1,772453..

Non stupisce dunque che dalla durata dell’anno solare divisa per 10 si possa ricavare un’approssimazione di π nel modo che vediamo qui di seguito

1/[³√(365,25 : 10) – 3] = 1/(³√36,525 – 3) = 1/(3,317900.. – 3) = 1/0,317900.. = 3,145634.. ≈ π = 3,141592..

Anche elaborando il 543 attraverso il logaritmo naturale arriviamo piuttosto direttamente a delle discrete approssimazioni di π

₅Ln (543 !) = -0,314669699763.. ≈ π/-10 = -0,314159264358..

(Ln 543) : 2 = 6,297109.. : 2 = 3,148554.. ≈ π = 3,141592..

Dunque, la connessione fra la struttura dei numeri che descrivono la durata dell’anno solare e di quello lunare è arricchita dal fatto che la terna pitagorica in essa contenuta ha una strettissima relazione con π.

Adesso non abbiamo tempo per fare un’analisi completa, però, prevedibilmente, anche la struttura di un numero come il 543 appare significativa. Per fare un solo esempio, se facciamo il rapporto fra il prodotto e la divisione sequenziale dei suoi componenti, viene fuori un numero sacro che abbiamo già trovato molte volte, il 144

(5 ∙ 4 ∙ 3) : (5 : 4 : 3) = 60 : 0,416666666.. = 144

6.

Dopo quel che abbiamo visto, pensare che la struttura di questi calendari, come peraltro anche quella della Piramide di Chefren, coincida con parti della struttura di questi fenomeni naturali solo per caso significa, secondo noi, passare dal pensiero scientifico a quello magico: ovvero, significa attribuire alla parola “caso” – non concettualizzata e non definita – la possibilità di risolvere qualsiasi situazione problematica di qualsiasi genere, indipendentemente dal contesto. In effetti, questo senso, la parola “caso”, nel pensiero di alcuni filosofi e di alcuni scienziati, oramai non si distingue più da una sorta di abracadabra intellettuale, che, se ha il difetto di non risolvere nessun problema scientifico e filosofico, ha il grande pregio di abolirli tutti per statuto.

Al contrario, noi sembra invece che tutti i dati che abbiamo raccolto quanto alle culture del Paleolitico e del Neolitico impongono almeno l’ipotesi che la ragione ultima tanto dei calendari Antico Egizio e Maya che della Piramide di Chefren debba essere ricercata proprio nella struttura dei rapporti del ciclo solare e lunare, che molto spesso sono stati adottati in contemporanea come differenti strumenti di misura del tempo (o come strumenti di misura di tempi cosmici differenti ma in vario modo sovrapposti e intersecati fra di loro). Come il Plateau di Giza nel suo complesso era – fra le altre cose – anche una rappresentazione di momenti diversi di differenti cicli stellari, così la Piramide di Chefren e i calendari solari Antico Egizio e Maya erano la rappresentazione delle profonde strutture matematiche con cui il Creatore ha generato i cicli solari e lunari per noi più rilevanti. Fra l’altro, se indagassimo anche a un livello piuttosto semplice la struttura del 1460 tipico del ciclo di Sirio, vedremmo che le sue parentele con quello solare e quello lunare verrebbero fuori in modo fin troppo chiaro. Banalmente, la somma dei suoi componenti è uguale a 11, ovvero a uno dei numeri cui allude il lato della Grande Piramide misurato in cubiti (infatti, dividendo il numero intero per le sue decine abbiamo che 440 : 40 = 11).

7.

Se adesso torniamo al 390, che abbiamo lasciato sospeso poco sopra, e lo elaboriamo un po’ (tenendo in considerazione che abbiamo scoperto che esso fa parte della struttura sia del ciclo solare e lunare, sia di quello di Saturno, Venere e Mercurio) ecco che scopriamo che questo numero è interessante anche per il suo rapporto con le costanti della fisica. Infatti, facendo per 4 volte consecutive il suo logaritmo naturale, otteniamo il rapporto fra il raggio classico del protone (1,535) e quello dell’elettrone (2,8194). Un rapporto che ritroveremo anche in seguito, in modo diverso, in relazione al ciclo scoperto da Charles Marcello, in cui ovviamente lo possiamo trovare anche per mezzo del 390

–₄Ln 390 = 0,544666505.. ≈ r_p/r_e = 0,544724160.. ≈ sen 33° = 0,544639..

Inoltre, 390 ∙ 2 = 780, numerologicamente parlando, non è altro che il tempo che intercorre fra le metà di due periodi retrogradi di Marte, pari a 780 giorni. Un ciclo questo che i Maya consideravano particolarmente sacro. Possiamo anche notare che 6 di questi cicli di Marte sono l’equivalente di 13 anni solari “puri” Maya o Antico Egizi di 360 giorni ciascuno: ma il 13 era appunto il numero caratteristico del calendario Maya Tzolkin: troviamo dunque in questo modo l’ennesima relazione ermetica fra il sistema calendario Maya e quello Antico Egizio. Un argomento che sarà oggetto di analisi in un lavoro successivo.

Ma, tornando all’analisi numerologica del 365,25 e del 354,36, se facciamo la somma di tutti i numeri che compongono la durata dell’anno solare e di quello lunare, troviamo in ambedue casi il 21.

3 + 6 + 5 + 2 + 5 = 21; 3 + 5 + 4 + 3 + 6 = 21;

Sommando le cifre che compongono il 21, abbiamo per due volte che 2 + 1 = 3. Questa somma è solo apparentemente insignificante, dato che la differenza fra 365,25 e 354,35 è pari a 3,3²: a livello numerologico si stabilisce così un ulteriore, potentissimo legame simbolico fra l’anno solare e quello lunare.

√(365,25 – 354,36) = √10,89 = 3,3;

Il quadro armonico-numerologico è completato dal fatto che il doppio logaritmo di 3,3 ci dà come risultato un valore vicinissimo a √π/10. Ma abbiamo visto sopra che tanto dal prodotto che dalla somma dell’anno solare e lunare è possibile ricavare valori vicinissimi a √π. Questo significa che la durata di questi periodi di tempo è stata costituita dalla Mente Divina proprio sul fondamento di √π

₂Ln 3,3 = 0,177244078.. ≈ √π/10 = 0,177245385.. (-1,3 ∙ 10^-6

Diciamo una cosa come questa, che la Mente Divina ha costituito la durata di questi due cicli cosmici sulla base di √π, del tutto consapevoli che nel nostro secolo un’espressione di questo genere tende a urtare gravemente con la sensibilità scientifica diffusa, se non proprio con il senso comune. Essa rappresenta per lo scienziato e l’intellettuale medio, laicizzato per definizione, non tanto uno scandalo intellettuale, ma più che altro una testimonianza di scarsa preparazione culturale, o di infantilismo filosofico – posto che la filosofia in quanto tale non venga considerata in sé e per sé un infantilismo. Ci sono molte persone che senz’altro la prenderanno, come il frutto di pura e semplice stupidità, oppure di un’astuzia: quale miglior modo di attirare l’attenzione su sé stessi che trovare un modo facile facile per “épater les bourgeois“? Ma non ci potrebbe essere impressione più errata. Noi abbiamo fatto questa affermazione perché risulta inevitabilmente dal materiale che abbiamo raccolto in questo e negli altri lavori che abbiamo pubblicato (e, dobbiamo dirlo, anche da una gran massa di materiale ancora inedito).

8.

D’altra parte, che una relazione fra l’anno delle fasi lunari e π esista lo si può mostrare in modo ancora più semplice. Ci basta il prodotto fattoriale della sua durata – in un’approssimazione che differisce dal numero comunemente accettato di meno di un millesimo – e il valore che otteniamo non è altro che π/2 moltiplicato per 10⁷⁵¹

354,35904969..! = 1,57079632.. ∙ 10⁷⁵¹ = π/2 ∙ 10⁷⁵¹

D’altra parte, il logaritmo naturale della potenza del 10 coinvolta in questa proporzione risulta poi essere un’approssimazione sperimentalmente possibile della costante di Planck

Ln 751 = 6,621405.. ≈ h = 6,626

Se poi andiamo a vedere il seno dell’angolo pari a 751° c’è davvero da trasecolare. Esso non è altro che una trasformazione numerologica dell’angolo di inclinazione della Piramide di Cheope misurato in gradi e sessantesimi di grado

sen 751° = 0,515038.. ≈ 51°50′ : 100 = 0,5150

L’inverso della sua tangente elevata alla quarta, non è altro che 1 + G

1/tg⁴ 751° = 1/0,130345176.. = 7,671937.. ≈ 1 + G = 7,6712

Il prodotto fattoriale del suo valore negativo diviso per 2 risulta praticamente pari alla costante di Dirac elevata al quadrato

– tg 751° ! : = -0,600860619..! : 2 = 2,223060592.. : 2 = 1,111530296.. ≈ ħ² = 1,112121318..

L’angolo di 751° ha caratteristiche identiche a quello di 31°: e la radice cubica di 31 è un’ottima approssimazione di π

³√31 = 3,141380.. ≈ π = 3,141592..

Anche il prodotto fattoriale della durata dell’anno solare si connette con π, sia pure in modo un po’ più indiretto e complesso di come abbiamo visto fino ad adesso

365,25 ! = 1,097751792382.. ∙ 10⁷⁷⁹

Se facciamo la radice del numero escludendo la potenza del 10, quella che ne risulta è un’approssimazione davvero buona di π_Cheope/3, e dunque anche della lunghezza del lato Est-Ovest della Camera del Re (pari a circa 10,478 metri) diviso per 10. Quindi, possiamo ricavarne facilmente un’approssimazione di π nel modo che vediamo qui sotto

√1,097751792382.. ∙ 3 = 1,047736509.. ∙ 3 = 3,143209.. ≈ π_Cheope = 3,142857..

Però, l’aspetto più interessante del prodotto fattoriale della durata dell’anno solare non è questo, ma invece proprio quel 779 che definisce la potenza del 10 che abbiamo qui sopra escluso dal calcolo. Infatti esso corrisponde a un angolo (quello di 59°) con caratteristiche complementari a quelle già analizzate di quello di 751°.

Questo fatto sembra rivestire un’importanza anche simbolica del massimo rilievo: con la complementarità trigonometrica del valore delle potenze 779 e 751 che contribuiscono a definire il prodotto fattoriale della durata dell’anno solare e di quella dell’anno delle fasi lunari, sembra che la Mente Divina abbia voluto alludere alla complementarità degli opposti principi simbolizzati dai due astri, il Principio Maschile e quello Femminile. Dunque, d’ora in avanti, quando in culture antiche o moderne troviamo simbolizzato il Principio Maschile dal Sole e quello Femminile dalla Luna, dobbiamo tener presente che dietro questo simbolo non c’è la fantasia sfrenata di popoli e di menti non sufficientemente evolute, ma anche cose molto serie e oggettive quali la matematica e la trigonometria a base 360.

9.

Si tenga presente che 779 + 751 = 1530 ci porta a un angolo con caratteristiche identiche a quello di 90°, e che anche i prodotti fattoriali di 779 e 751 non sono, diciamo così, scientificamente neutri. Infatti, il prodotto fattoriale di 779, escludendo la potenze del 10, non è altro che il rapporto fra la massa del protone ed il suo raggio classico

779 ! = 1,089389.. ( ∙ 10¹⁹¹⁶) ≈ m_p/r_p = 1,6725 : 1,535 = 1,089576..

E qui troviamo delle connessioni profonde fra il prodotto fattoriale di 779 la somma delle durate del ciclo solare, lunare e dell’anno delle eclissi, dato che se ne facciamo la radice

⁸¹√(365,25 + 354,36 + 346,6) = ⁸¹√1066,21 = 1,089885.. ≈ m_p/r_p = 1,089576..

Anche la potenza del 10 che definisce 779 ! – cioè 1916 – appare molto significativa, perché la sua radice quarta corrisponde alla lunghezza di Planck più 5: dunque corrisponde anche a un valore sperimentalmente possibile di h = 6,626

⁴√1916 = 6,616051.. ≈ ℓ_P + 5 = 6,616252.. ≈ h = 6,626

Invece, il seno dell’angolo di 1916° corrisponde all’inverso della costante di Dirac al quadrato

1/sen 1916° = 1/0,898794046.. = 1,112601940.. ≈ ħ² = 1,112121318..

Passando al prodotto fattoriale di 751 possiamo per prima cosa osservare che, esclusa la potenza del 10, il logaritmo naturale del numero che otteniamo è vicino a (6 + 1/ɸ_Cheope)/10 e dunque anche alla costante di Planck divisa per 10

751 ! = 1,9381834201527483979384145552783 ∙ 10¹⁸³⁵

Ln 1,93818342.. = 0,661751153.. ≈ (6 + 1/ɸ_Cheope)/10 = 0,661782155.. ≈ h/10 = 0,6626

Il 1835 della potenza è vicinissimo al rapporto fra la massa del protone e quella dell’elettrone, che è pari a 1836: e, di nuovo, sembra molto interessante che partendo dalla complementarità Sole/Luna, maschile/femminile, siamo finiti a quella fra le due particelle atomiche dotate di carica uguale e contraria. D’altra parte, se facciamo per 4 volte il logaritmo naturale di 1835, quello che otteniamo è ancora una volta uno dei punti di partenza della nostra analisi, ovvero la durata dell’anno delle fasi lunari, però divisa per 10³

₄Ln 1835 = -0,354464.. ≈ 354,36/-10³ = -0,35436

In sintonia con tutto quel che abbiamo visto fino ad adesso, possiamo ricordare che anche l’inverso del raggio classico dell’elettrone corrisponde con buona approssimazione alla durata dell’anno lunare, moltiplicata per 10¹²

2,81794 ∙ 10^-15 = 354,869.. ∙ 10¹² ≈ 354,36 ∙ 10¹²

10.

Dunque, lungi dal rappresentare un’immaginifica metafora, il nostro riferimento a un’intelligenza che trascende l’empiria risulta ancor più fondata quando ricordiamo che un simile modo di procedere della Mente Divina lo abbiamo trovato anche nella creazione di molte grandezze fisiche, che sono caratterizzate dal fatto di contenere nella loro intima struttura dei legami con altre grandezze fisiche importanti. Legami che poi sono il frutto delle potenzialità armoniche di π, di ɸ, del 10 e del numero di Eulero. Quindi non ci stupisce di trovare che anche la costante fisica che ha il legame più profondo con la nozione di tempo, ovvero la velocità della luce, si costituisce parimenti come cifra contenente complesse strutture armoniche. Infatti, se prendiamo un’approssimazione del valore di c espresso in metri al secondo pari a 299.792.454 (il valore comunemente dato per buono è 299.792.458), possiamo notare che la somma delle prime 3 cifre corrisponde a 2 + 9 + 9 = 20, quella delle seconde a 7 + 9 + 2 = 18, quella delle terze a 4 + 5 + 4 = 13. Ma 20, 18 e 13 sono i numeri caratteristici del sistema calendario Maya Haab’-Tzolkin. Se adesso facciamo la radice cubica del prodotto di questi 3 numeri dobbiamo prepararci a una sorpresa, dato che troviamo il valore caratteristico della massa del protone, moltiplicato per 10

³√(20 ∙ 18 ∙ 13) = ³√4680 = 16,726893.. ≈ 10m_p = 16,725

Questa non è l’unica acrobazia numerologica che si potrebbe ottenere dalla triade di numeri sacri che caratterizza il sistema Haab’-Tzolkin e, come abbiamo appena scoperto, anche la velocità della luce. Per esempio, se eleviamo il 18 alla 13sima potenza e poi facciamo la radice 32sima abbiamo che

³²√18¹³ = 3,235597231.. ≈ 2ɸ = 3,236067977..

Se poi facciamo il logaritmo in base 10 del prodotto fra i due esponenti, quella che troviamo è una discreta approssimazione di ɸ_Cheope²

log (32 ∙ 13) = log 416 = 2,619093.. ≈ ɸ_Cheope² = 2,619834..

Inversamente, se eleviamo il 13 alla 18sima potenza e poi facciamo la radice 192sima otteniamo un’ottima approssimazione della tangente della Grande Piramide, che è a sua volta un’approssimazione di √ɸ

¹⁹²√13¹⁸ = 1,27183914.. ≈ tg 51°,817.. = 1,271549464.. ≈ √ɸ = 1,272019649..

Concludiamo notando che la Grande Piramide contiene delle relazioni organiche, ovvero internamente armoniche, anche nel suo perimetro espresso in metri, che, come possiamo dedurre dalla foto sotto, è pari a circa 230,253 + 230,391 + 230,454, + 230,357 = 921,455 metri.

La misura media dei lati viene 921,455 : 4 = 230,36375. E subito possiamo notare che, sommandola a quella dell’altezza (146,595113..) e poi facendo la radice 16sima, quel che viene fuori è il prodotto fattoriale di ɸ

¹⁶√(230,36375 + 146,595113) = ¹⁶√376,9588.. = 1,448802183.. ≈ ɸ ! = 1,449229602.. (-3,964.. ∙ 10^-4

Se invece facciamo la radice 1024sima del rapporto fra i prodotti fattoriali di lato e altezza, otteniamo una discreta approssimazione del numero caratteristico del raggio classico del protone

¹⁰²⁴√(230,36375 ! : 146,595113 !) = 1,534361.. ≈ r_p = 1,535

Dalla differenza dei due prodotti fattoriali possiamo invece ricavare un’ottima approssimazione di -√2 + 1 con una sequenza di 5 logaritmi naturali

₅Ln (230,36375 ! – 146,595113 !) = -0,414252745124.. ≈ -√2 + 1 = 0,414213562..

Inoltre, facendo per 4 volte il logaritmo naturale del prodotto, otteniamo una buona approssimazione del valore della carica unitaria c_u/10 = 1,6022/10; facendo per 2 volte il logaritmo in base 10, quel che viene fuori è un’approssimazione di h_Planck/10

₄Ln (230,36375 ∙ 146,595113) = ₄Ln 33770,19996235375 = -0,160118.. ≈ -c_u/10 = -0,16022

₃log (230,36375 ∙ 146,595113) = ₃log 33770,19996235375 = 0,655957.. ≈ h_Planck/10 = 0,655

Ma nelle misure in metri della Piramide sembra sia nascosta una magia matematica ancor più stupefacente e dunque anche più complessa. Se arrotondiamo la lunghezza del lato a 230,36 e facciamo il prodotto delle centinaia per le decine, per i decimi per i centesimi, ci troviamo di nuovo di fronte a un numero sacro, il 54 ∙ 2 = 18 ∙ 6 = 108 con cui ci siamo incontrati più volte nelle analisi precedenti

200 ∙ 30 ∙ 3/10 ∙ 6/10² = 108

Se invece arrotondiamo a 230,363 e facciamo il rapporto delle centinaia, con le decine, i decimi, i centesimi, e i millesimi che compongono il numero, dobbiamo tenerci forte, perché ci troviamo di fronte a una stranissima sorpresa, che, è il caso di dirlo, sfiora il miracolo matematico. Infatti, il numero che vediamo qui sotto è composto, compreso il periodo, dalla sequenza ordinata dei numeri decimali, escluso l’8

200 : 30 : 3/10 : 6/10² : 3/10³ = 123456,79012345679012345679012346

Questa cifra, divisa per 10⁵, ci dà una buona approssimazione di 2/ɸ_Cheope

123456,790123../10⁵ = 1,234567901.. ≈ 2/ɸ_Cheope = 1,23564310..

Ma, a parte questo, si nota che la differenza fra la cifra “tonda” o “ideale” del perimetro – che dovrebbe essere 230 ∙ 4 = 920 metri – e quella effettiva è pari a 921,455 – 920 = 1,455 metri (ovvero a circa un centesimo dell’altezza della Piramide, pari a 146,59.. metri). A questo punto, diventa inevitabile notare che se facciamo il rapporto fra il perimetro espresso in cubiti (440 ∙ 4 = 1760) e quello espresso in metri, dobbiamo prepararci a una sorpresa, che rischia di causare emozioni che vanno al di là di un semplice lo stupore

1760 : 921,455 = 1,910022735.. ≈ (1,455 ∙ 2) – 1 = 1,91

In pratica, si può ricavare il rapporto fra la misura del perimetro espressa in cubiti e quella espressa in metri, a partire dalla differenza fra la cifra “ideale” e quella “reale” del perimetro espresso in metri.

Viene spontanea la domanda: da chi o da cosa possono aver imparato i progettisti della Grande Piramide i metodi armonici con cui l’hanno costruita, se non da relazioni matematiche di questo genere, o da fenomeni naturali come il ciclo solare e quello delle fasi lunari, ovvero, in ultima analisi, da Dio stesso?

11.

Queste potranno anche parere delle domande retoriche. Ma l’immagine che mostriamo qui sotto dimostra in modo geometrico-visivo l’intima relazione fra le proporzioni della Piramide e quelle del rapporto fra il raggio della Terra e quello della Luna. L’immagine che in questo contesto ci interessa è quella sulla sinistra, ma aggiungiamo anche quella a destra, elaborata da Vermard e Mathieu, che trova una relazione un po’ più complessa ma proprio per questo, in un certo senso, anche più significativa

Nell’immagine a sinistra è riportato il rapporto fra il raggio della Luna e quello della Terra, pari a circa 0,273 che, come subito si nota, corrisponde al numero caratteristico della costante che definisce il rapporto fra la carica e la massa dell’elettrone (5,273..) meno 5. Ma questa non è la cosa più importante. Infatti, questo rapporto spaziale, imprevedibilmente, ha qualcosa a che vedere con il periodo della Terra attorno al Sole, dato che se dividiamo la durata dell’anno solare per 10² e facciamo l’inverso, quello che otteniamo è giustappunto il rapporto fra il raggio della Luna e quello della Terra

1/(365,25 : 10²) = 1/3,6525 = 0,273785..

Come oramai ci aspettiamo, questo numero ha una relazione profonda tanto con π_Cheope = 22/7 che con ɸ_Cheope che, molto meglio che con le parole, possiamo comprendere osservando l’equazione che vediamo qui sotto.

[³√(-0,273785..!)^22/7]² = [³√(1,258397..^22/7)]² = (³√2,05927..)² = 1,272246..² = 1,618610.. ≈ ɸ_Cheope = 1,618590..

Quindi, per incredibile che possa sembrarci, tutta quella serie di complicatissimi rapporti strutturali che riguardano i numeri che descrivono la durata dei calendari solare e lunare riguardano in modo immediato e diretto anche il rapporto fra il raggio del Sole e quello della Luna. Questo fatto sembra rafforzare in modo decisivo anche quanto avevamo scritto sopra riguardo alla relazione fra la distanza media della Terra e la Luna, che è pari a circa 60,7 il raggio terrestre. Trasformando numerologicamente questo dato in un angolo di 60°,729.. scopriamo che elevando la tangente al quadrato otteniamo un valore pari a 10/π

tg² 60°,729407921.. = 1,784124116..² = 3,183098861.. = 10/π

Parimenti facendo la sommatoria di tangente, seno e coseno, arriviamo a un numero molto vicino a π,

sen + cos + tg 60°,729.. = 0,872320.. + 0,488934.. + 1,784124.. = 3,145379.. ≈ π = 3,141592..

Invece, elevano al quadrato la somma di seno e coseno e dividendola per c = 2,9979246, quella che otteniamo è un’approssimazione molto buona di 1/ɸ

(sen + cos 60°,729..)²/c = 1,361255..² : 2,99792,46 = 1,853015.. : 2,9979246 = 0,618099.. ≈ 1/ɸ = 0,618033..

E qui non possiamo non ricordare l’analisi che abbiamo fatto riguardo al modo un po’ strano con cui i Francesi chiamano il 70, ovvero “tre-venti-dieci”. Avevamo ipotizzato che questa poteva essere la sottolineatura di un valore simbolico-scientifico di questo numero, che viene definito, diciamo così, per scomposizione. La nostra analisi è stata piuttosto approssimativa, ma adesso siamo in grado di sottolineare che la frazione (70 : 60)² = 1,361111.. ha davvero qualcosa a che vedere con la relazione fra la Terra e la Luna. Una relazione di cui non abbiamo ancora terminato di indagare le proporzioni.

Infatti, la distanza media della Terra dalla Luna espressa in chilometri è pari a circa 384.000 chilometri. Se prendiamo per buona quest’approssimazione pari a 384.941, 138.., scopriamo che il tempo che la luce mettere a raggiungere la Terra dalla Luna è esattamente pari alla radice quarta del numero di Eulero

384941,138371.. : 299792,46 = 1,284025.. = ⁴√e

Se facciamo la radice c⁵ = 2,9979246⁵ = 242,160625.. di quest’approssimazione della distanza media fra la Terra e la Luna, quello che otteniamo è il numero caratteristico della costante di Dirac

^242,160625..√384941,138371.. = 1,054544.. ≈ ħ = 1,054571..

12.

È davvero difficile trovare le parole giuste per commentare risultati di questo genere. Tutto quel che possiamo dire è che, se i calcoli che abbiamo effettuato sono giusti, non solo non possiamo più parlare di un universo dominato dal caso, ma da un determinismo onnipresente che, a quel che pare, è la regola segreta di tutto ciò che accade. Un determinismo però, in cui decisive non sono le quantità misurabili ed osservabili. Esse invece, in un modo criptico, sono a loro volta precostituite in un complesso sistema di relazioni matematiche che non hanno nulla a che fare con l’empiria. Questo sistema, che ancora non siamo in grado di comprendere e dominare, ad ogni passo della nostra analisi sembra però emergere in modo sempre più chiaro e inesorabile. E ciò significa che il Numero si pone categorialmente come antecedente alla realtà sensibile: ne è il modello e ne costituisce la sostanza.

Questa non è una nostra idea originale. Essa deriva – oltre che, ovviamente, da Platone – anche dalla lettura di questo passo di de Santillana e von Dechend, in cui questi autori, con mirabile acume, hanno intuito la visione scientifica che doveva sottostare al mito e al suo codice astronomico ermetico

Era quello un tempo ricco di un’altra conoscenza andata poi perduta, che ricercava principi diversi [da quelli di verificabile e non verificabile]; esso fornì la lingua franca del passato, la sua era una conoscenza di corrispondenze cosmiche che trovavano riprova e suggello di verità entro uno specifico determinismo, anzi, un sovradeterminismo, soggetto a forze totalmente prive di ubicazione. Il fascino e il rigore del Numero facevano obbligo che le corrispondenze fossero esatte in molte forme (in questo senso Keplero fu l’ultimo degli arcaici). La molteplicità di rapporti visti o intuiti portò l’idea di un punto focale in cui l’universo appariva determinato non su un solo livello, ma contemporaneamente su molti: questo era il contrassegno dell’ “ideazione panmatematizzante”. Tale idea può benissimo aver condotto a un’armonia prestabilita su un numero di livelli infinito. Leibniz ci ha dimostrato fino a che punto si può arrivare, se ci si serve di strumenti moderni: l’universo dei singoli destini per tutto il tempo a venire, concepito tutto in unico istante da una «folgorazione» della mente divina. Un qualche Leibniz pitagorico preistorico o protostorico, la cui esistenza è tutt’altro che inconcepibile, può benissimo aver accarezzato questo sogno, spingendosi fino al limite con più innocenza di quanto non fece quel nostro sapiente in età storica. Se si parte dal potere del Numero, è pensabile in questa prospettiva tutta una logica: fata regunt orben, certa stant omnia lege.

G. de Santillana – H. von Dechend, Il Mulino di Amleto, Adelphi, p. 100

Letta nel contesto, questa frase appare molto diversa da come appare se letta isolatamente. Gli autori, pur con un certo rammarico (e a volte, anzi, con un certo rancore), danno per scontata una supremazia della scienza occidentale moderna su quella antica, che apprezzano per la sua armonia e per la sua capacità di trovare un senso alla vita umana. Perciò, ogni volta possono, cercano di valorizzare il genio di chi ha creato la scienza astronomica implicita nel mito, che ha colto risultati inferiori a quelli degli scienziati moderni solo a causa della scarsità dei mezzi a disposizione.

Ebbene, a partire dalle scoperte che stiamo facendo, noi siamo arrivati al punto di dover riconoscere una evidente superiorità della scienza antica su quella moderna. Quel che de Santillana e von Dechend definiscono come un “sovradeterminismo”, fondato sul potere e sul rigore del Numero, in cui l’universo appare determinato su molteplici o forse addirittura su infiniti livelli, non ci appare più come il sogno di una mente ingenua, ma come l’essenza stessa della realtà. Quelle forze che loro definiscono “totalmente prive di ubicazione” si possono definir così solo perché, come Dio, siccome sono in ogni luogo, non sono in realtà da nessuna parte.

Se i calcoli che stiamo facendo sono giusti, altra conclusione non sembra possibile.

Capitolo 6:

L’ANALISI STRUTTURALE DEL NUMERO COME POSSIBILITÀ DI COMPRENDERE L’ESSENZA MATEMATICA DELL’UNIVERSO: INDAGINE SUL CICLO DI SIRIO E SU QUELLI DI SATURNO, GIOVE, VENERE E MERCURIO

1.

Tutto quel che abbiamo visto fino ad adesso, diciamo la verità, sembra troppo bello o, a seconda dei punti di vista, troppo brutto per essere vero. Partendo dalle relazioni che il ciclo di Charles Marcello intrattiene con altri cicli cosmici, siamo arrivati a scoprire delle mirabilie matematiche di cui nessuno ha mai osato ipotizzare l’esistenza. E queste mirabilie matematiche non sono qualcosa che troviamo nei libri scritti dagli esseri umani, ma bensì in quel Grande Libro della Natura in cui il Creatore ha proiettato le divine proporzioni della sua stessa Mente!

Dopo un paio di secoli di illuminismo, evoluzionismo e positivismo logico, sembra impossibile prendere anche minimamente sul serio delle idee di questo genere. Oramai ci siamo abituati a pensare che l’ordine matematico è un qualcosa che la mente umana proietta sul Caos: troviamo in quel cassetto vuoto che è la materia in continuo divenire solo quello che, consapevoli o meno, ci abbiamo messo dentro. Altro non ci può essere o, se ci fosse, non potremmo concepirlo.

Questo è un modo di pensare oramai piuttosto comune. Ma anche ove non ci si spinga fino a questa strana sorta di estremismo agnostico, difficilmente in ambito scientifico si parla di un intrinseco ordine matematico del mondo. Non c’è da stupirsene, se già il Keplero ventenne, scrivendo a un altro studente, confessava di non credere più che il numero fosse l’essenza dell’universo: era già felice di sapere che potesse servire in qualche modo a comprenderla. Il numero si era trasformato in una lente di ingrandimento, e non era già più l’oggetto scrutato.

Oggi anche i credenti più convinti non osano più addentrarsi in questioni che oramai appaiono superate, non tanto dall’epoca, ma dai fatti. Quando in ambito cristiano-cattolico si parla di un concetto come quello di “evoluzione guidata” l’immagine che si ha in mente sembra un quella di un genitore che guida un bambino docile e/o riottoso. Oppure quella del classico artigiano che, usando questa volta i tempi smisurati dell’evoluzione, trasforma una materia grezza, la cellula primordiale, in forme con il tempo più complesse e più perfette, ultimo l’uomo moderno dotato di coscienza (cioè di quel che un tempo si chiamava “anima”) dopo qualche miliardo di anni di lenta formazione. Nessuno sembra essere più attratto dall’idea di un Dio che dà un ordine matematico al mondo: un ordine che poi risulta non solo comprensibile, ma anche oggettivamente dimostrabile. L’oscura certezza che permea la nostra epoca sembra proprio quella contraria: se c’è qualcosa di cui la matematica è riuscita a farci certi, è che il mondo non ha affatto alcun ordine matematico. L’insanabile conflitto fra meccanica einsteiniana e meccanica quantistica non basta e avanza a dimostrarlo pienamente?

Ci siamo abituati a pensare in questi termini, e di colpo vediamo che i numeri del codice astronomico sacro individuati da de Santillana e von Dechend cominciano a saltar fuori un po’ dappertutto, nella fisica sperimentale come nell’astronomia: proprio nel bel mezzo di un momento storico in cui siamo diventati certi che acrobazie matematiche del tipo immaginato da Keplero sono impossibili anche per Dio.

Ma se l’impossibile sembra verificato dai fatti ci resta ancora una via d’uscita: non sarà mica che questa volta abbiamo davvero a che fare con il Caso? Il Caso che – come quando compaiono numeri consecutivi alle estrazioni del lotto – ha prodotto delle relazioni che sembrano frutto di un’intelligenza, ma che poi si rivelano un frammento d’ordine in un universo completamente frammentario e caotico?

2.

La tentazione lasciare il saldo timone della logica e lasciar cullare il nostro pensiero nella deriva dello scetticismo fine a sé stesso è molto forte, occorre dirlo. Abbandonare le proprie inclinazioni intellettuali consolidate diventa tanto più difficile quanto più col tempo si sono irrigidite dogmi quanto più severamente ribaditi quanto meno ripensati e messi in discussione. Ma la voglia di risolvere il problema usando il lassismo intellettuale come metodo ci passerà sempre di più, via via che ci renderemo conto che la realtà tutta si costituisce sulla base di proporzioni armoniche di cui una possibile espressione è proprio quel codice di numeri sacri scoperto da de Santillana e von Dechend. È solo il fatto che si costituisce di numeri interi che finora ci ha impedito di coglierne tutta la meravigliosa complessità.

Possiamo cominciare con il ciclo di Sirio. Un ciclo che dura 1460 anni solo ed esclusivamente se lo si osserva da un posto come Giza. Noi però, come forse il lettore ricorda, abbiamo individuato all’interno della struttura del numero che descrive la durata del ciclo solare: 365,25. Infatti abbiamo visto che moltiplicando la parte intera per quella decimale, quel che viene fuori è proprio 365 ∙ 0,25 = 1460.

D’altra parte, si nota che il ciclo di Sirio, calcolato a partire da un calendario di 365 giorni come quello Antico Egizio, va a sincronizzarsi con il ciclo solare proprio in un periodo di circa 1460/1461 anni. È questo il tempo che occorre a Sirio per presentarsi di nuovo alla levata eliaca al solstizio d’estate. Viene quasi voglia di pensare che gi Antichi Egizi siano andati ad abitare in Egitto proprio perché in quel punto la stella più luminosa del firmamento ha un ciclo dalla durata esattamente corrispondente a quella contenuta nella struttura di quello solare.

Un’ipotesi di questo genere, che sulle prime ci sembra del tutto assurda, diventa di colpo sensata quando dividiamo il ciclo di Sirio per 144, e ci rendiamo conto che il risultato è un valore molto significativo perché straordinariamente prossimo a 10 + 1/ɸ⁴.

1461 : 144 = 10,145833333.. ≈ 10 + 1/ɸ⁴ = 10,145898033.. (-6,470041..

Il risultato non sarebbe abbastanza impressionante, se non scoprissimo che la differenza con il valore esatto è praticamente pari a 4ɸ ∙ 10^-5.

6,470041.. ∙ 10^-5 ≈ 4ɸ ∙ 10^-5 = 6,4721.. ∙ 10^-5 (-2,094256..

E qui, di nuovo, sembra di avere a che fare con un mezzo miracolo matematico, o magari anche con un miracolo e mezzo, se subito dopo non scoprissimo che questo non è altro che il primo anello di una catena di differenze fra valori esatti e approssimazioni costituita di numeri matematicamente molto significativi, e appartenenti tutti, diciamo così, alla stessa famiglia. Infatti la differenza fra questa approssimazione di 4ɸ con il valore esatto è praticamente pari (Ln π – 1)² ∙ 10^-3. Anche se dobbiamo riconoscere che l’approssimazione di (144 ∙ 10^-6)² non è affatto male

2,094256.. ∙ 10^-8 ≈ (Ln π – 1)² ∙ 10^-3 = 2,094673.. ∙ 10^-8 ≈ (144 ∙ 10^-6)² = 2,0736 ∙ 10^-8

D’altra parte, se dividiamo il ciclo precessionale per quello di Sirio, e andiamo a vedere cosa succede le cose non vanno in modo molto diverso. Infatti, anche se di nuovo otteniamo un numero non intero, di nuovo, se prendiamo la parte decimale e la moltiplichiamo per 4, ecco che otteniamo un risultato praticamente pari a 10/π

26000 : 1461 = 17,796030116..;

0,796030116.. ∙ 4 = 3,184120465.. ≈ 10/π = 3,183098861..

Questo significa che inversamente, possiamo ottenere un’ottima approssimazione della durata del ciclo precessionale a partire dal ciclo di Sirio e da 10/π. E anche in questo caso la differenza con il numero esatto appare significativa, e, si direbbe, quasi organica con il calcolo svolto. Infatti essa è più o meno pari ₄Ln 1461

[17 + (10/4π)] ∙ 1461 = 17,795774.. ∙1461 = 25999,626859.. (-0,373140.. ≈ ₄Ln 1461 = -0,376643..

Né può sfuggire il fatto che la radice quarta del ciclo di Sirio diviso per 10 alla quarta è un’ottima approssimazione del numero d’oro

⁴√(1460/10⁴) = 0,618141.. ≈ 1/ɸ = 0,618033..

3.

Abbiamo cambiato i cicli oggetto della nostra analisi, ma i numeri che utilizziamo o che in vario modo saltano fuori sono sempre gli stessi. Sono quelli che furono codificati nelle misure della Grande Piramide: π, ɸ, 10 e il numero di Eulero. E se adesso ci volgiamo ad analizzare i rapporti numerologici fra i cicli dei pianeti inclusi in quello individuato da Charles Marcello, scopriamo che essi sembrano contenere a loro volta dei numeri sacri. E non solo, come abbiamo visto in The Snefru Code parte 13, quando osservati dal punto di vista della Terra, ma anche e soprattutto quando osservati prendendo come punto di riferimento il Sole.

Per fare un esempio che riguarda direttamente l’oggetto di questo lavoro, Venere impiega 225 giorni a girare intorno al Sole e 243 a girare su sé stesso. La differenza fra queste due cifre è appunto 18, ovvero un numero sacro che, come abbiamo visto, è la base di molti numeri sacri, che non ne sono altro che un multiplo (es. 54 = 3 ∙ 18; 72 = 4 ∙ 18; 108 = 6 ∙ 18; 144 = 8 ∙ 18; 360 = 20 ∙ 18): non è un caso che questo numero è quello che caratterizza il calendario solare Maya Haab’.

Oltre a ciò, se facciamo la moltiplicazione dei membri di queste due cifre, otteniamo dei numeri che, come in una catena, sono divisibili per il risultato dei loro componenti. E questi numeri sono a loro volta numeri sacri.

2 ∙ 4 ∙ 3 ∙ 2 ∙ 2 ∙ 5 = 480; 4 + 8 = 12; 480 : 12 = 40

Sul 12 è naturalmente del tutto inutile sottolineare lo smisurato significato storico, astronomico e religioso. Quanto al 40 invece, conviene ricordare che è il numero forse più importante di quel codice matematico sacro che troviamo nella Bibbia, dove il 40 risulta senz’altro una delle cifre ripetute più frequentemente, e che in certi contesti diventa quasi una cantilena che accompagna lo svolgersi degli avvenimenti (cfr. la fuga la vita di Mosè, la fuga dall’Egitto etc.): 40 sono le sillabe di ogni strofa dei Veda, 40 sono anche gli anni che Ulisse sta lontano da Itaca. Abbiamo già visto molte cose nei lavori passati attorno al suo possibile significato scientifico. Qui possiamo notare che il logaritmo in base 10 di 40 ci da il valore della carica elettrica unitaria c_u = 1,6022..

log 40 = 1,602059.. ≈ c_u = 1,6022

Per avere idea di come funzionassero questi antichi codici matematici, al 40 possiamo aggiungere un altro numero che nella Bibbia è considerato particolarmente sacro, il 7. Facendo di nuovo il logaritmo in base 10 otteniamo il numero caratteristico della costante che descrive la massa del protone m_p = 1,6725

log 47 = 1,672097.. ≈ m_p = 1,6725

4.

I risultati che abbiamo già conseguito ci potrebbero convincere a lasciar perdere Venere e a passare a un altro pianeta, perché potremmo anche pensare di aver già enucleato tutto o quasi tutto il suo significato ermetico-numerologico. E invece ancora molto ci resta da fare. Tanto per cominciare, a Venere è connesso un altro numero sacro fra quelli scoperti da de Santillana e von Dechend nella struttura del mito, il 108, che, ovviamente, compare in molte varianti, definite da multipli di 10 di una stessa radice

Come si sa, nella battaglia finale degli dèi, le legioni schierate dalla parte dell’«ordine» sono i guerrieri morti, gli Einherjarr caduti combattendo sulla terra e che le Valkyrien hanno trasportato nel Valholl a dimorare con Odhinn – un tema sovente ricordato della poesia eroica. Dicono i Grìmnismàl (23): «Cinquecento porte e quaranta ancora / sono del possente edificio della Valholl / ottocento Einherjarr escono da ciascuna porta / allorché vanno a combattere contro il Lupo». In totale sono dunque 432.000, un numero significativo fin da antica data, anzi, sicuramente di significato antichissimo perché è anche il numero delle sillabe dei Rg-Veda (40 sillabe per strofa), che, assieme al 108, compare insistentemente nella tradizione indiana. Secondo Censorino (De die natali, 18), 10.800 è anche il numero degli anni assegnati da Eraclito alla durata dell’Aion, mentre Berosso fa durare il Grande Anno babilonese 432.000 (= 108.000 ∙ 4) anni; 10.800, inoltre, è anche il numero di mattoni dell’altare del fuoco indiano (Agnicayana).

G. de Santillana – H. von Dechend, Il Mulino di Amleto, pp. 196-197

Nel nostro caso, troviamo che il 108 compare diviso per 10². Ma è del tutto chiaro che, trovandoci in un sistema matematico fondato fra l’altro anche sul 10, quel che conta è, diciamo così, la forma del numero, non la sua materia. Dunque, che il 108 compaia come 10800 o come 1,08 non ha importanza. Come quasi tutti gli altri numeri sacri, 108 è un multiplo del 18, e dunque è connesso con un angolo che si può derivare direttamente dal numero d’oro, dato che il suo coseno è l’inverso di -1/2ɸ

243 : 225 = 1,08 = 108/10²

Questa fatto, fra le altre cose, ci dà modo di enucleare un altro frammento del significato del ciclo solare e di quello delle fasi lunari, dato che in un modo vagamente imparentato a questo, vediamo che il 108 caratterizza il prodotto numerologico della durata dell’anno lunare (354,36), mentre dal prodotto numerologico della durata dell’anno solare e di quello lunare esclusi i decimali possiamo ricavare un 54 moltiplicato per 10²

(3 ∙ 5 ∙ 4 ∙ 3 ∙ 6) = 1080

(3 ∙ 6 ∙ 5) ∙ (3 ∙ 5 ∙ 4) = 90 ∙ 60 = 5400 = 54 ∙ 10²

Oppure, se facciamo la somma del periodo di Venere attorno a sé stesso e di quello attorno al Sole 243 + 225 = 468 e la interpretiamo numerologicamente come un angolo, vediamo che esso è un equivalente di quello di 72° e di quello di 108°, sia pure con i segni di alcuni parametri invertiti

sen 468° = sen 72° = sen 108°

cos 468° = -cos 72° = -cos 108° = -1/2ɸ

tg 468 = -tg 72° = tg 108°

Fra l’altro, si nota che il 468 è uno di quei numeri divisibili in modo perfetto per la somma dei numeri che lo compongono, che anche in questo caso dà come risultato 4 + 6 + 8 = 18. Il risultato della divisione ci dà un altro numero caratteristico dei calendari Maya, vale a dire il 468 : 18 = 26. Questo significa che se con il ciclo solare e quello lunare abbiamo ricostruito i numeri caratteristici del calendario Haab’, con il ciclo di Venere abbiamo ricostruito quelli del calendario Tzolkin (che, come noto, aveva come punto in comune con quello Haab’ il 20). Il suo numero caratteristico era il 13, che però può risultare benissimo dal 26, dato che, fra l’altro, il numero di giorni di questo ciclo era il 260. E qui è bene ricordarci che il ciclo di Venere era uno di quelli che i Maya consideravano più importanti, assieme ovviamente a quello solare.

5.

Ma l’esempio forse più scioccante di come i numeri sacri individuati da de Santillana funzionino nel determinare quella che i Pitagorici chiamavano “l’armonia delle sfere” ci viene da Mercurio, un altro dei pianeti che fanno parte del ciclo individuato da Charles Marcello, dove incontriamo delle relazioni a cui, come si dice, chi non vede non crede. Arriveremo pian piano alle relazioni più stupefacenti, passando per quelle che, pur non avendo degli aspetti così “miracolosi” come quelli che ci apprestiamo a descrivere, hanno però un grande interesse per l’argomento che stiamo trattando. Esse fungeranno così da preparazione a una relazione che, presentata ex abrupto, servirebbe più a disorientare che a stupire.

Come prima cosa, possiamo notare che la circonferenza orbitale di Mercurio è pari a 360.000.000 km, ovvero numerologicamente pari alla durata di un anno “puro” Antico Egizio e Maya (360 giorni) moltiplicata per 10⁶. E qui troviamo un’intima connessione numerologica con Giove, il cui periodo attorno al Sole è pari a circa 11,86 anni solari, e dunque a 4332 giorni, che corrispondono a loro volta con ottima approssimazione a 12 anni puri Antico Egizi e Maya (4332 : 360 = 12,033.., cioè, in pratica, 12 cicli di 360 giorni più 12 giorni “bisestili”). Di passaggio possiamo notare che il prodotto dei componenti di 4332 è 4 ∙ 3 ∙ 3 ∙ 2 = 72, e che la somma è invece pari appunto a 12, e che tanto il 4332 che il 72 sono divisibili per 12. Infatti

4332 : 12 = 361

72 : 12 = 6

E qui possiamo notare che 361 risulta da 19²: abbiamo così la possibilità di stabilire un contatto tanto con il ciclo di Metone che con quello di Saturno, Venere e Mercurio, che adesso potremmo dividere per la radice di 361 (che è la durata di un mese di Giove) ottenendo quegli stessi risultati che abbiamo visto sopra procedendo invece che con la durata del ciclo di Metone. Né possiamo trascurare il fatto che, se dividiamo 361 per 10⁵ e facciamo il prodotto fattoriale, otteniamo un’approssimazione di c – 2 = 0,9979246 che sfiora la perfezione

361/10⁵ ! = 0,00361 ! = 0,9979290.. ≈ c – 2 = 0,9979246

E qui, per avere di nuovo un’idea di come in questo meraviglioso sistema armonico ogni parte rimandi continuamente al tutto, conviene sottolineare che facendo il prodotto fattoriale di (c – 1)/10, otteniamo un’ottima approssimazione della tangente della sezione aurea dell’angolo giro 360/ɸ = 222°,492235..

(c – 1)/10 ! = 0,19979246 ! = 0,918223847.. ≈ tg 222°,492235.. = 0,9160819..

A questo proposito, possiamo notare anche il fatto che un valore del tutto simile a (c – 1)/10 ! è quello che viene fuori da un numero molto particolare, ovvero da quel numero che, diviso per il suo logaritmo in base 10, ci dà il numero di Eulero col segno meno. Si nota anche che il numero è piuttosto vicino a c_u – 1

x : log x = -e; x = 0,60102749594626548.. ≈ c_u – 1 = 1,6022 – 1 = 0,6022

0,60102749594626548.. : -0,221105659337383.. = -2,7182818284590452..

Questo numero è interessante non solo perché si pone come trait d’union fra il 10 e il numero di Eulero, ma anche perché ad esso si connettono altri numeri piuttosto interessanti. Infatti, se facciamo 10^x con questa cifra e poi dividiamo il risultato per 10, otteniamo un numero di cui possiamo trovare una quasi perfetta approssimazione del valore negativo facendo di nuovo il logaritmo in base 10

log (10^{0,60102749594626548..} : 10) = log (3,990501661291321.. : 10) = 0,3990501661291321..

0,3990501661291321.. + log 0,3990501661291321.. =

= 0,3990501661291321.. -0,39897250405373452..) = 7,766207.. ∙ 10^-5

Ed è a questo punto, di nuovo in un modo al tempo stesso meravigliosamente complesso e meravigliosamente semplice, che troviamo la connessione di questo numero armonico tanto con (c – 1)/10! che con il ciclo di Saturno, Venere e Mercurio. Infatti, se facciamo il suo logaritmo naturale, troviamo appunto un valore molto simile a (c – 1)/10 ! = 0,918223847..

-Ln 0,3990501661291321.. = 0,918668140.. ≈ (c – 1)/10 ! = 0,918223847.. tg 360°/ɸ = 0,91608191..

6.

L’accenno che abbiamo fatto a Giove merita di essere proseguito, perché anche i “numeri” di questo pianeta sembrano aver profondamente a che fare con il codice astronomico sacro individuato da de Santillana e von Dechend. Giove infatti ruota su sé stesso in 596 minuti, così che il rapporto fra la durata del suo giorno e del suo anno (che dura 4332 ∙ 24 ∙ 60 = 6238080 minuti) da luogo a un numero molto alto, ma non certo insignificante. Infatti si nota che quella che vediamo sotto non è altro che la misura del lato Est-Ovest della Camera del Re, pari π/c ∙ 10 =10,479 metri circa, moltiplicato per 10³ (teniamo anche conto che il risultato sarebbe esatto se il periodo di Giove intorno a sé stesso fosse di 595,280660 minuti invece che 596).

6238080 : 596 = 10466,577181..

Facendone la radice ottava otteniamo una buona approssimazione di 10/π. La differenza con il valore esatto è praticamente identica all’inverso di un anno solare Antico Egizio o Maya di 365 giorni

⁸√10466,577181.. = 3,180354891.. ≈ 10/π = 3,183098861.. (-0,00274.. ≈ -1/365 = -0,002739..

Se invece moltiplichiamo il periodo di Giove attorno al Sole per quello che impiega a girare intorno a sé stesso (continuando a esprimere il tempo in minuti) e poi ne facciamo la radice-π, quello che otteniamo non è altro che il valore della costante di Dirac elevato al quadrato e moltiplicato per 10³

^π√(6238080 ∙ 596) : 10³ = ^π√3717895680 : 10³ = 1,112551727.. ≈ ħ² = 1,112121318.. (

7.

Date le premesse, la sorpresa che abbiamo annunciato riguardo a Mercurio deve essere veramente grossa, perché già il sistema di relazioni che abbiamo individuato riguardo a Venere e a Giove sembra già di per sé piuttosto impressionante: in caso contrario, rimarremo piuttosto delusi. Ma il sistema armonico in cui ci muoviamo è al tempo stesso regolare ed estremamente vario, e anche questa volta vedremo che le lancette dell’universo vanno a toccare le cifre giuste: solo in un modo che nessuno al mondo si sarebbe mai sognato di prevedere. Ed è proprio questo il motivo per cui ci siamo sentiti di affermare che la sorpresa che ci apprestiamo a descrivere è veramente grossa.

Per introdurci all’argomento, possiamo notare che Mercurio percorre la sua orbita attorno al Sole in soli 88 giorni, più velocemente di qualsiasi altro pianeta. Allo stesso tempo, Mercurio ruota lentamente su se stesso, dato che per farlo impiega 59 giorni terrestri.

Come è accaduto in precedenza, le operazioni con i componenti di queste cifre ci portano fin da subito a dei risultati molto interessanti. Per esempio, il prodotto delle decine per le unità ci dà un numero – la somma dei cui componenti ci dà 18 – che corrisponde sia a un multiplo del 360, che a un multiplo del 18.

80 ∙ 8 ∙ 50 ∙ 9 = 288000; 8 + 8 + 2 = 18

288000 : 360 = 800

288000 : 18 = 16000

Se adesso facciamo il rapporto fra i risultati delle due divisioni, otteniamo il 200, cioè un altro numero caratteristico del calendario solare Maya Haab’, il 20, moltiplicato per 10. Ci manca solo il 5 per completare i numeri di questo calendario, che risulta completo se moltiplichiamo l’inverso di 200 per 10²

16000 : 800 = 200

Oppure, se dividiamo il rapporto delle decine per le unità otteniamo 18/10.

(80 : 8) : (50 : 9) = 10 : 11/2 = 1,8

L’inverso di 11/2 = 5,5 è, molto significativamente, un 18 periodico, e la sua radice 32sima è una discreta approssimazione dell’inverso della costante di Dirac

1/5,5 = 0,1818181818..

1/³²√0,181818181.. = 1/ 0,948120.. = 1,054717.. ≈ ħ = 1,054571..

Se invece facciamo il prodotto di tutti i numeri che compongono le due cifre, il risultato che otteniamo è un’altra di quelle cifre divisibili per 18 da cui, sommando i numeri che le compongono, si ottiene come risultato 18. Se poi lo dividiamo per 18², da un lato, siamo rimandati ai risultati conseguiti da Miquel Pérez Sanchez intorno alle misure della Piramide. Dall’altro, di nuovo alla durata dell’orbita di Mercurio attorno al Sole. Infine, anche allo strano modo in cui i Francesi chiamano il 90 “quatre-vingt-dix”, cioè “quattro-venti-dieci”, segnalando così il particolare rapporto del 90, per esempio, con l’80

8 ∙ 8 ∙ 5 ∙ 9 = 2880; 2 + 8 + 8 = 18

2880 : 18 = 160

2880 : 18² = 8,8888888.. = 10/(90 : 80) = 10/1,125 = 8,888888..

Sembra molto interessante il fatto che procedendo in modo inverso si possa, non solo dedurre un rapporto interno del 90 “francese” da uno dei “numeri di Mercurio”, ma che da questo rapporto si possa anche risalire a un’ottima approssimazione del numero caratteristico della carica elettrica unitari c_u = 1,6022

1/[(2880 : 18²) – 8]⁴ = 1/0,8888888.. = 1,125⁴ = 1,601806.. ≈ c_u = 1,6022

8.

Questi risultati sembrano già piuttosto significativi, ma ancora non abbiamo ancora toccato, diciamo così, il lato veramente magico dei “numeri di Mercurio”. Possiamo cominciare a esporlo moltiplicando 88 per 59 e facendo la radice. In questo modo otteniamo un valore molto prossimo a 72

√(88 ∙ 59) = √5192 = 72,05553413860728574149502756704

Una prima sorpresa è che se facciamo il prodotto fattoriale -72,055.. e poi facciamo la radice 4374sima otteniamo un valore di ħ che differisce di pochissimo da quello che otteniamo dalla sommatoria di seno, coseno e tangente di π/2

⁴³⁷⁴√-72,055534..! = 1,054482.. ≈ sen + cos + tg π/2 = 1,054458..

Se adesso procediamo come abbiamo fatto nel caso del rapporto fra il ciclo individuato da Charles Marcello e quello di Metone, e dunque togliamo la parte intera di questo risultato e facciamo l’inverso dell’avanzo decimale, troviamo ancora una volta un numero sacro, vale a dire il 18

1/0,05553413860728574149502756704 = 18,006941767325910717686878445881

Se togliamo ancora una volta la parte intera, troviamo un altro numero sacro

1/0,006941767325910717686878445881 = 144,05553413860728574149502753863

Se togliamo la parte intera, ritroviamo ancora una volta il 18,006941767325910717686878445881 da cui eravamo partiti

1/0,05553413860728574149502753863 = 18,006941767325910717686887657481

Se facciamo il rapporto fra questi due numeri, troviamo un risultato vicinissimo a 8. Però non è chiaro se la differenza con il numero intero dipenda dal numero o dalla quantità di decimali che la calcolatrice di Windows è in grado di supportare

144,05553413860728574149502753863 : 18,006941767325910717686878445881 =

= 7,9999999999999999999999999984218 ≈ 8

Questa incredibile catena di relazioni – in cui otteniamo un multiplo di un numero intero sacro attraverso l’inverso dei decimali – è completata dal fatto che facendo la radice sesta di 0,055534.. e di 0,006941.. ∙ 8, possiamo ottenere in entrambi i casi una buona approssimazione di 1/ɸ_Cheope

⁶√0,05553413860728574149502753863 = 0,617674.. ≈ 1/ɸ_Cheope = 0,617821..

⁶√(0,006941767325910717686887657481 ∙ 8) =

= ⁶√0,055534138607285741495101259848 = 0,617674.. ≈ 1/ɸ_Cheope = 0,617821

Questo però non è ancora tutto. Se adesso dividiamo l’approssimazione del 18 che abbiamo appena trovato per 18 pari, e poi facciamo il logaritmo in base 10, quel che viene fuori è il numero caratteristico della costante che descrive la massa del neutrone m_n = 16748, moltiplicato per 10^-4

log 18,006941767325910717686878445881 : 18 = 1,674550.. 10^-4 ≈ m_n ∙ 10^-4 = 1,6748 ∙ 10^-4

Inoltre, sembra molto importante il fatto che quell’approssimazione di 1/ɸ_Cheope che abbiamo visto sopra è vicinissima a quella che ci serve per ottenere c – 2 = 0,9979246 nel modo che vediamo qui sotto,

1/[(1/0,617674975..)² – (1/0,617674975..)] = 1/(2,621078250.. – 1,618974444..) = 1/1,002103806.. =

= 0,99790061.. ≈ c – 2 = 0,9979246

9.

Andando avanti con le nostre analisi, ci troveremo altre volte di fronte a relazioni di questo genere, e cercheremo di dargli un’occhiata più a fondo. Per il momento le abbandoniamo per fare una riflessione, a cui ci introduce un passo tratto da un libro a cui torneremo molte volte nel corso di questo lavoro. Quasi come a un filo di Arianna che ci guiderà lungo i meandri del pensiero astronomico, sia esso religioso o scientifico o puramente matematico, che fu patrimonio dei nostri padri.

È necessario comprendere una volta per tutte che l’abisso tra il mondo arcaico e il nostro era vasto quanto la scienza: i prodigi di esattezza e di calcolo non erano sufficienti a colmarlo; l’unica a poterlo fare era la carta astronomica. La situazione è stata riassunta in poche parole da Whitehead: «La nostra scienza è stata fondata sull’ubicazione univoca e sulla concretezza fuori posto». La fisica moderna ha trasformato questi termini in quesiti. Per Newton la cosa aveva la forza dell’evidenza: «Nessuna persona dotata di capacità di comprensione razionale crederà che una cosa possa agire dove non è». Fu Newton stesso a porre il primo quesito formulando la teoria della gravitazione universale: matematicamente inoppugnabile, fisicamente inspiegabile. Egli dovette limitarsi ad accettarla: «Io non la capisco, e non intendo inventare ipotesi». La risposta dovette attendere Einstein; essa consisté in una pura razionalizzazione matematica che fece piazza pulita dell’ubicazione e della concretezza. L’edificio di Descartes giacque in rovina. Ciò non ostante, la mente dell’uomo civile rimase tenacemente aggrappata a entrambi i principi, ritenendoli in accordo col comune buon senso: tipico caso di un’abitudine diventata seconda natura.

G. de Santillana – H. von Dechend, Il Mulino di Amleto, Adelphi, p. 91

Chissà, forse è giunto il momento di cambiare davvero la nostra visione del mondo e della storia. E, assieme ad essa, anche il nostro comune buon senso. Forse è giunto il momento di prendere sul serio e portare fino in fondo la strada che ha preso la scienza nel secolo scorso. Non è facile capire dove altri potrà o vorrà arrivare. Per quanto ci riguarda, già a partire da The Snefru Code parte 3 noi siamo arrivati a un punto che sembra al tempo stesso incredibilmente avanzato e incredibilmente antico. Siamo arrivati a ipotizzare che la frase di origine Pitagorica «le cose sono numeri» corrisponde alla piena e perfetta verità di una scienza fisica che arrivi infine a prendere sul serio i suoi presupposti. Che le costanti della nostra scienza sono tutte numeri puri, integrate in un sistema matematico-trigonometrico in cui numeri come la costante di Planck o quella di Newton vanno accanto a π, ɸ, il 10 e il numero di Eulero. Che questo sistema è capace di descrivere, senza lacune o soluzioni di continuità, tutto l’universo, dalla particella più infima fino alle galassie, impensabilmente estese e impensabilmente lontane. Che una Mente Divina, per mezzo di queste forme matematiche, ha generato l’universo traendolo all’essere per mezzo di un etere matematico, assimilabile al concetto platonico di “invisibile-indeterminato”.

Capitolo 7:

IL CICLO DI SATURNO, VENERE E MERCURIO: UN ULTERIORE APPROFONDIMENTO DELL’INDAGINE SULLE BASE DELLE INDAGINI ASTRONOMICO-MATEMATICHE FIN QUI SVOLTE

1.

Quello che abbiamo scoperto riguardo al ciclo individuato da Charles Marcello (che, come vedremo poi, non solo non confuta le teorie di Bauval, ma le integra e ne amplia il significato), il suo integrarsi in modo meravigliosamente armonico con le misure della Piramide, e con i cicli lunari e planetari che abbiamo tanto a lungo analizzato, è senz’altro una conferma del fatto che uno degli scopi delle tre Piramidi maggiori sia anche quello di scandire l’inizio e la fine di questo ciclo astronomico. Che, dobbiamo notare, non è affatto naturale: ovvero, non si fonda su eventi astronomici “oggettivi” come quello scoperto da Bauval. In effetti, se anche a Giza nessuno avesse costruito le Piramidi, resta il fatto che Orione ha raggiunto il punto più basso all’orizzonte nel 10500 a.C. e che le stelle della sua Cintura avevano proprio quella inclinazione. In contemporanea, il Sole era entrato nel segno del Leone alla levata eliaca dell’equinozio di primavera: il che sarebbe un fatto egualmente constatabile anche se non ci fosse stata lì la Sfinge ad “osservarlo” nel momento in cui si è verificato.

Invece, nulla di questo vale per il ciclo di Saturno, Venere e Mercurio. Il fatto che le sue proporzioni matematiche siano in continuità con i ritmi generali del sistema solare e dell’universo tutto non ci deve ingannare. Esso infatti è stato artificialmente creato

1) con la costruzione delle Piramidi in quel particolare punto della Terra per rappresentare quella determinata configurazione celeste che si è verificata a Giza nel 10500 a.C. circa

2) con l’adozione di quel particolare rapporto di rappresentazione con il cielo che però, ovviamente, come qualsiasi convenzione semantica, si sarebbe potuto tranquillamente invertire, senza con ciò alterare l’esattezza della rappresentazione.

Per comprendere questo fatto fondamentale, possiamo osservare l’immagine qui sotto, dove viene chiaramente indicato un metodo alternativo di rappresentare le 3 stelle della Cintura di Orione, speculare a quello di fatto adottato. L’adozione di questo metodo alternativo – oppure di costruzioni di scala diversa – avrebbe probabilmente impedito la creazione di quello splendido spettacolo notturno che ogni 2737 anni si verifica sul cielo di Giza. La sua adozione si spiega dunque, molto probabilmente con il proposito di includere nei compiti del paesaggio sacro anche la creazione di questo nuovo ciclo celeste

Ma la conferma che l’indicazione del ciclo individuato da Charles Marcello appartiene ai compiti che furono affidati dagli antichi architetti alle tre Piramidi maggiori di Giza è anche una conferma di quanto abbiamo ipotizzato negli ultimi lavori che abbiamo pubblicato su questo sito. Ovvero, che attraverso le relazioni fra cicli cosmici si può arrivare alla deduzione/codificazione di costanti fisiche di primaria importanza e delle loro interne relazioni armoniche. Questo, a sua volta, significa che davvero l’universo è un sistema dove tutto è connesso con tutto. Dunque è logicamente illegittimo fare distinzioni fra la geometria in quanto sistema di relazioni astratte e le osservazioni empiriche che possiamo fare riguardo all’atomo o al sistema solare. Come diceva Platone, la matematica non è altro che una via di mezzo fra la realtà sensibile e il Mondo delle Idee. Queste tre realtà, pur essendo di diversa natura, si trovano in uno stato che Wittgenstein definiva di “isomorfismo logico”. Possiedono però gradi di astrazione e dunque di purezza molto diversi: nullo la realtà sensibile, medio la matematica, pieno l’Iperuranio.

2.

Una ulteriore conferma della piena e perfetta integrazione del ciclo di Mercurio, Venere e Saturno nella grandiosa meridiana precessionale che è il paesaggio sacro di Giza è la sua strettissima relazione con un altro ciclo lunare, che sembra confermare il lavoro ermeneutico che abbiamo svolto. Si tratta del ciclo di retrogradazione dei nodi della Luna, che dura circa 18,61 anni solari. Questo rapporto, come ci apprestiamo a scoprire, ci rimanda di nuovo a Mercurio, dato che la somma della durata della sua orbita attorno al Sole e del tempo che impiega a girare intorno a sé stesso è uguale a 88 + 59 = 147, cifra che corrisponde in modo quasi perfetto al rapporto fra il ciclo di Saturno, Venere e Mercurio e quello della retrogradazione dei nodi della luna

2737 : 18,61 = 147,0714669..

Di nuovo, dobbiamo notare che il conto non è perfettamente pari. Però, di nuovo, possiamo arrotondare la cifra con una certa tranquillità. Non solo perché la differenza sembra di nuovo abbastanza significativa, dato che corrisponde in modo praticamente perfetto 1/14, ovvero all’inverso di un ciclo di fasi lunari (il che mette in relazione il risultato della divisione con il divisore). Noi però possiamo facilmente togliere anche quel “quasi” perché sappiamo che il ciclo di retrogradazione dei nodi della Luna dura leggermente di più di 18,61 anni, e perché il rapporto con i 2737 anni del ciclo di Saturno, Venere e Mercurio vada perfettamente a 147 + 1/14 ci basta alterare la sua durata della minuscola entità che vediamo qui sotto

2737 : 18,610004856.. = 147 + 1/14

Inoltre, 147,071.. corrisponde in modo praticamente perfetto alla distanza minima della Terra dal Sole, che varia fra i 147 e i 147,1 milioni di chilometri.

Ma, a parte questo, noi sappiamo che arrotondare le cifre era una prassi degli antichi sacerdoti-astronomi, che ricorrevano a un tale stratagemma per inserire numeri di rilievo astronomico o scientifico-matematico nei miti cosmologici. Per esempio, il Numero della Bestia – il famigerato 666 – allude senz’altro al 6,666.. periodico (100/15, o 2/3 etc.), che a sua volta, come abbiamo visto in dettaglio in The Snefru Code parte 9, contiene in codice molti valori matematici e scientifici importanti. A partire da esso infatti si possono ricostruire sia la costante di Newton che quella di Planck, in aggiunta all’angolo di 360°/6,666.. = 54°, che, attraverso il numero d’oro, contiene un numero enorme di nozioni matematico-scientifiche (ricordiamo che sen 54° = 1/(2/ɸ)).

E che questa nuova relazione cosmologica che abbiamo scoperto possa avere un profondo interesse scientifico e matematico ce lo conferma il fatto che facendone la radice ottava, otteniamo un valore molto prossimo a 1 + sen 60° = 1 + (√3 : 2). Un’altra cifra che, come abbiamo visto in The Snefru Code parte 3, è a sua volta capace di contenere un gran numero di nozioni scientifiche molto importanti (oltre a quelle geometriche, che tutti ben conoscono).

⁸√147 = 1,866013007.. ≈ 1 + sen 60° = (1 + √3 : 2) = 1,866025403..

Oppure, se andiamo a controllare il seno dell’angolo di 147°, scopriamo che corrisponde in modo praticamente esatto al rapporto fra il numero caratteristico del raggio classico del protone e quello dell’elettrone 1,535/2,81794 = 0,544724.. Come abbiamo visto nei lavori passati, da questo rapporto si può facilmente ricavare la massa del protone, e dalla massa del protone poi mille altri dati

sen 147° = 0,54463903.. ≈ r_p/r_e = 0,54472408..

(2 r_p/r_e)⁶ = (2 ∙ 0,54472408…)⁶ = 1,08944816..⁶ = 1,672012.. ≈ m_p = 1,6725

A parte questo, si nota che il 147 sembra anche un’allusione numerologica all’altezza della Grande Piramide, che in origine era alta circa 146,5 metri. Dunque, da questo punto di vista, se arrotondata verso l’alto, essa poteva alludere al ciclo di Mercurio, Venere e Saturno. Oppure, arrotondata verso il basso, e diventando così un 146, poteva alludere a uno dei due numeri caratteristici del ciclo di Sirio, il 1460 (l’altro, come abbiamo visto, era il 1461).

3.

Il fatto che questo nuovo ciclo celeste misurato dalle Piramidi di Giza si inserisca bene nel contesto del complesso codice scientifico con cui furono progettate l’arte e l’architettura sacre Antico Egizie è forse la prova più importante della sua appartenenza alle originarie intenzioni dei costruttori. Ma non bisogna neppure trascurare il fatto che esso si inserisce in un modo che pare davvero armonico e lineare anche nei conteggi riguardanti il ciclo precessionale. Ricordiamo che in The Snefru Code parte 13, avevamo calcolato che un ciclo precessionale un po’ idealizzato, pari a 26000 anni di 365 giorni ciascuno (e questa era precisamente la durata del calendario solare Antico Egizio, come di quello Maya, che abbiamo analizzato in quella sede), corrisponde a 1396 cicli di retrogradazione dei nodi della Luna.

Questo significa che il ciclo di retrogradazione dei nodi e l’allineamento fra i 3 pianeti e le Piramidi arrivano a sincronizzarsi con il ciclo precessionale – cioè a finire e a iniziare di nuovo con la fine e l’inizio di un ciclo precessionale – ogni 1396 ∙ 147 = 205212 cicli precessionali di quel tipo, cioè ogni 5.335.512.000 anni di 365 giorni, cioè ogni 1.947.461.880.000 giorni. Su quel 205212 ci sarebbero molte cose da osservare, ma diciamo soltanto che è un’altra cifra che risulta divisibile per la somma dei numeri che la compongono (2 + 5 + 2 +1 + 2 = 12; 205212 : 12 = 17101). Quanto all’altra cifra, notiamo che facendone per due volte consecutive il logaritmo in base 10 otteniamo una buona approssimazione del rapporto fra la massa e il raggio del protone

₂log 1947461880000 = 1,089533.. ≈ m_p/r_p = 1,6725 : 1,535 = 1,089576..

Però dobbiamo tralasciare queste analisi, che sarebbero per altro molto interessanti, ma che ci prenderebbero troppo spazio. Qui ci preme invece di osservare che questo periodo di tempo si connette in modo sorprendentemente armonico anche con il sistema calendario Maya, dato che corrisponde a 2.496.746.000 cicli di Marte di 780 giorni ciascuno, oppure a 3.334.695.000 cicli di Venere di 584 giorni ciascuno, oppure in 7.490.238.000 anni Tzolkin, di 260 giorni ciascuno.

Questo ciclo corrisponde anche a un numero molto caratteristico di cicli di Sirio che, anche se non è pari, risulta non di meno piuttosto interessante. Infatti, 1.947.461.880.000 giorni, divisi per 1460 anni di 365,25 giorni ciascuno, danno un risultato molto vicino a un multiplo della durata effettiva dell’anno solare

1947461880000 : (1460 ∙ 365,25) = 365,1958932.. ∙ 10⁴ giorni ≈ 10.000 anni di 365,25 giorni

Se dividiamo questo risultato per 365,25, in effetti andiamo a ottenere un numero molto vicino al numero di giorni contenuto nei 2737 anni del ciclo di Mercurio, Venere e Saturno, diviso per 10². La differenza fra le due cifre è uguale alla costante di Planck meno 5 (e, lo ricordiamo (ɸ + 1/ɸ)² = 5)

3651958,932.. : 365,25 = 9998,518636.. ≈ (2737 ∙ 365,25)/10² = 9996,8925 (+ 1,626136 ≈ h – 5 = 1,626

4.

Questi fatti sembrano acquistare ancora maggior rilevanza perché anche il periodo di Saturno intorno al Sole si inserisce piuttosto bene nel quadro dei conteggi effettuati tenendo presente questo ciclo precessionale un po’ idealizzato. Infatti, in un ciclo precessionale formato da 26000 anni Haab’ di 365 giorni ciascuno – per un totale di 9490000 giorni solari – vi sono un numero di periodi di Saturno attorno al Sole – ciascuno pari a 29,458 ∙ 365,25 = 10759,5345 giorni solari – che risulta

9490000 : 10759,5345 = 882,008417..

Arrotondando a 882, questo significa che in quel periodo di 205212 cicli precessionali si succedono anche 180996984 rivoluzioni di Saturno attorno al Sole. Ricordiamo che il ciclo di Saturno, a livello numerologico, si connette piuttosto bene sia con il ciclo solare che quello lunare terrestri, dato che il tempo di una rivoluzione di Saturno attorno al Sole è pari a 29,458 anni terrestri (pari a 10759,5345 giorni e a 258228,828 ore): vi è quindi una quasi perfetta corrispondenza numerologica fra questa cifra e la durata di un mese sinodico lunare pari 29,5306 giorni solari. E, in effetti, dividendo il numero di giorni del tempo di rivoluzione di Saturno per quello del mese lunare abbiamo che

(29,458 ∙ 365,25) : 29,5306 = 364,35

Una cifra molto vicina al numero di giorni di un anno solare. Considerando che il periodo di rotazione di Saturno dura solo 10 ore e 45 minuti circa (o 10,75 ore), contro le 258228,828 ore della sua orbita attorno al Sole, il rapporto viene più o meno pari alle ore di un giorno terrestre (24) moltiplicate per 10³.

258228,828 : 10,75 = 24021,286.. ≈ 24 ∙ 10³

5.

É chiaro che all’intellettuale occidentale medio, dei cicli cosmici di questa spaventevole entità, suddivisi in un complesso intreccio di sottocicli il cui conteggio non ha maggior utilità che quello maggiore, suscitano ogni sorta di perplessità. Cifre di una certa taglia – 5.335.512.000 anni, e non un giorno di meno! – di solito ci sembrano talmente assurde che non siamo capaci di prenderle nella sia pur minima considerazione, almeno se riferite a qualcosa che siamo disposti a chiamare un “calendario”. L’abisso d’angoscia che sono capaci di spalancare numeri di questo genere si trasforma di solito in una battuta ironica, o, ancora più spesso, in pura e semplice indifferenza.

Questo accade perché nell’ambito della nostra cultura il tempo assume significato in relazione alla durata della vita di un individuo e dei suoi più o meno immediati dintorni storici. Perciò, parlare di un secolo non è poi molto diverso dal parlare dell’eternità, o giù di lì. Per noi lo scopo della vita, posto che esista, consiste negli scopi mondani che un individuo può pensare di raggiungere nel giro di una settantina o ottanta anni. Proiettandoci su figli, nipoti e pronipoti, possiamo immaginare al massimo i due o tre secoli. Oltre, c’è solo quella laica fine del mondo ch’è l’eterno oblio. Oppure, per i cristiani, quella che coincide col ritorno apocalittico di Gesù.

Ma non ci stancheremo mai di ricordare che nelle culture come quella Antico Egizia, indifferenti agli individui e agli avvenimenti storici connessi con le vite individuali, la nostra ironia o il nostro stupore parrebbero egualmente fuori luogo. Con gli occhi fissi alla “vita dei milioni di anni“, vale a dire agli eterni ritorni dei cicli cosmici, i secoli e i millenni potevano apparire tanto fugaci e vani come a noi paiono i minuti. Nell’ambito di una tradizione senz’altro imparentata con quella Antico Egizia, quella Induista, un Giorno di Brahma o kalpa, ha una durata che supera i 4 miliardi di anni. Un anno di Brahma è composto di 360 kalpa, e una vita intera di Brahma ne dura 100: dunque, quel ciclo di 5.335.512.000 anni che abbiamo individuato non arriva a rappresentare nemmeno un millesimo della sua durata.

Ma era proprio a queste scale di tempo che miravano gli antichi calendari, e dunque anche il ciclo connesso a quell’allineamento sacro individuato a Giza da Charles Marcello. Su queste scale di tempo, la sua associazione con il ciclo precessionale risulta perfettamente ragionevole e, anzi, ci aiuta a comprendere che un concetto come quello di “ragionevolezza” tende a cambiare radicalmente in relazione alle visioni metafisiche che vengono adottate. Volenti o nolenti, se vogliamo capire il motivo per cui il Plateau di Giza è stato costruito nel modo in cui di fatto è stato costruito, dobbiamo cercare di calarci nel punto di vista dei suoi costruttori che, con ogni evidenza, non aveva nulla a che fare con il nostro. E chissà che così facendo non possiamo arrivare a concepire l’astronomia e i cicli astronomici in modo diverso da come di fatto facciamo e siamo inclini a fare.

Per adesso però possiamo senz’altro concludere che il ciclo individuato da Charles Marcello è senz’altro uno di quelli che sono stati codificati nell’impianto archeoastronomico, ovvero in quella gigantesca meridiana precessionale che è il paesaggio sacro di Giza e dintorni. A provarlo non c’è solo l’esattezza della sovrapposizione contemporanea di Saturno, Venere e Mercurio alle Piramidi. Al di là di questo, lo prova il fatto che questo ciclo si pone in un rapporto armonico con un gran numero di altri cicli cosmici, e che questo rapporto armonico si fonda su quegli stessi numeri sacri sulla cui base sono stati generati tanto il Plateau di Giza che l’intero universo.

Si tratta però, come abbiamo visto, di un ciclo artificiale, che non corrisponde a qualcosa che potrebbe essere individuato se non attraverso l’allineamento con una struttura costruita da esseri umani. Il motivo di questa creazione sembra essere quello di fare in modo che attraverso le Piramidi si possano misurare anche molti altri cicli che risultano connessi con il ciclo individuato da Charles Marcello. Ci riferiamo in particolare ai quattro cicli lunari: l’anno delle fasi, l’anno delle eclissi, il ciclo di Metone, e quello della retrogradazione dei nodi (con la probabile aggiunta di un ciclo di congiunzioni fra Giove e Saturno).

Nella parte successiva di questo lavoro, tratteremo il rapporto fra le teorie di Bauval e quelle di Andrew Collins, in cui vedremo come questa rete di connessioni intessuta dal ciclo Saturno, Venere e Mercurio con Luna e pianeti vanno a intersecarsi con un modo altrettanto complesso di segnare le “ore dell’eternità” lungo quel quadrante cosmico che è il cielo del Nord, in cui la Terra traccia il cerchio della precessione. Ma prima di passare all’analisi di questa parte del problema è bene fermarci per una breve riflessione.

6.

Chiunque sia arrivato a leggere queste parole si sarà reso conto della straordinaria difficoltà di decodificare il codice matematico con cui quella gran quantità di dati astronomici è stata criptata in questo ciclo cosmico artificialmente generato attraverso la particolare collocazione delle tre Piramidi maggiori sulla piana di Giza. Arrivare a comprenderlo ha implicato, fra l’altro, un inizio di comprensione di strutture geometriche-matematiche che ci erano del tutto ignote. In questo e negli ultimi lavori che abbiamo pubblicato su questo sito ci siamo resi conto che la Grande Piramide è stata generata attraverso quella stessa matematica con cui Dio ha generato il cosmo. Una struttura armonica, unitaria, che si dipana dal mondo delle particelle subatomiche fino alle profondità smisurate degli spazi cosmici.

Questa matematica, che non per gioco ma per fedeltà all’essere abbiamo definito, “matematica divina”, ci resta ancora in gran parte del tutto ignota. La nostra esplorazione è ancora agli inizi e, sebbene alcuni rapporti ci siano diventati meno enigmatici, ancora noi non sappiamo, per esempio, come mai Dio ha scelto certi numeri piuttosto che altri per generare l’atomo e i suoi componenti. Ci domandiamo dunque: nell’ambito di questo sistema matematico ci sono possibilità di scelta? Dio avrebbe potuto creare – per esempio – il protone in modo diverso da come l’ha creato e, alterando in proporzione tutti gli altri numeri, creare un universo retto da una diversa armonia?

È del tutto chiaro che in questo momento noi non sappiamo rispondere a questa domanda. Non solo. In questo momento non sappiamo neppur dire se sia logicamente corretto personla.

Ma anche altre questioni, sia pure di vastità e importanza molto minori, sono in questo momento al di là della nostra capacità di comprensione. Per esempio: alla scienza occidentale sono occorsi due secoli di studi per cominciare a capire l’impianto archeoastronomico di Giza: per poterlo decriptare sono occorsi gli sforzi di un gran numero di ricercatori, dotati di potenti strumenti di calcolo astronomico e matematico computerizzato, che a loro volta hanno richiesto lo sviluppo di una scienza e di una tecnica che fino a qualche decina di anni fa erano impensabili. Questo, lo ripetiamo, solo per decriptare il senso astronomico del sito. Quindi, di un linguaggio già approntato e di una gigantesca struttura già realizzata.

Ma ora domandiamoci: come si è potuta costruire una cosa del genere? Se tanti sforzi e tanta conoscenza sono stati indispensabili per decifrare la struttura, quali e quanti sforzi saranno stati necessari per progettarla? Come si è arrivati a quella conoscenza tanto minuziosa e profonda dell’infinitamente grande e dell’infinitamente piccolo, del sistema solare come dell’atomo, che ha permesso di comprimerli nei numeri che formano il codice sacro, ricostruita da de Santillana e von Dechend?

Ci rendiamo conto che un domandare di questo genere appare vertiginoso. Ma, al tempo stesso, è inevitabile. Noi siamo arrivati a poter realizzare certi calcoli, e attraverso di essi a comprendere certi tipi di connessioni, solo da qualche decennio. Ma migliaia e migliaia di anni fa come si è potuti arrivare a concepire il numero come struttura organica, connessa in una sorta di rete neuronale con tutti gli altri numeri, e non come nome proprio di un punto di una successione amorfa? Come si sono potuti dedurre i numeri caratteristici del sistema calendario solare Maya (360, 5, 20, 18) e di quello Antico Egizio (360, 5, 12, 30) a partire da quelli dell’anno solare e di quello delle fasi lunari? Come si è potuto capire che l’armonia divina che regge il cosmo la si può comprendere solo ed esclusivamente a partire dall’adozione del sistema metrico decimale, privato del quale lo scienziato e il matematico, per quanto capaci, si trovano di fronte a un cosmo che appare un caos puntiforme di numeri casuali?

Non solo noi non abbiamo ancora la più pallida idea di come rispondere a queste domande, ma nemmeno di come possiamo fare a porcele in un modo scientificamente sensato. Tutto quel che sappiamo è che questa gente aveva a disposizione una conoscenza scientifico-matematica dell’universo talmente vasta e profonda, talmente al di là delle nostre capacità di comprensione, che noi non siamo capaci di neppure immaginarla. E in questa incapacità riposano in questo momento anche tutte le metafore con cui pur saremmo tentati di esprimerla. Possiamo però tentare di fare ancora qualche passo avanti nella comprensione della struttura interna del numero, andando ad analizzare nella parte successiva un tipo di operazione che si fonda sulla sua scomposizione: il prodotto fattoriale

Capitolo 8:

UN TENTATIVO DI ALLARGARE LA NOSTRA COMPRENSIONE DELL’INTERNA STRUTTURA DEL NUMERO: INDAGINE SULLE CONNESSIONI DEL PRODOTTO FATTORIALE CON LE COSTANTI SCIENTIFICHE

1.

Abbiamo visto sopra a più riprese che l’armonia del sistema matematico si proietta anche su un’operazione come quella del prodotto fattoriale. L’unica forse fra quelle tipiche della nostra matematica in cui emerge, sia pure in modo indiretto, la struttura interna del numero, e la sua relazione con quelli che possiamo definire come i suoi componenti. E nelle pagine precedenti abbiamo visto che il prodotto fattoriale si integra in modo perfetto con quel sistema armonico con cui è stato generato l’universo, così che possiamo legittimamente pensare che anche questo genere di operazione possa essere rimasto finora largamente inesplorato, almeno per alcuni aspetti. Per avere un’idea del cammino che ci rimane da fare per comprendere l’antica scienza e l’antica matematica che furono codificate in un paesaggio sacro come quello di Giza, possiamo andare a dare un’occhiata a questa particolare operazione matematica, che, prevedibilmente, contiene degli aspetti che non sono stati finora presi nella dovuta considerazione.

Come noto, il prodotto di numeri fattoriali maggiori di 0 e minori di 1 ha un andamento un po’ strano. Partendo da 1 e scendendo verso il basso, il prodotto fattoriale è maggiore del numero di partenza solo fino a un certo punto, e solo fino a un certo scende assieme al numero che scegliamo. Poi al di sotto una certa soglia, prende a risalire, così che Lim_x→0 x ! = 1, proprio come Lim_x→1 x ! = 1.

Per farci un’idea di quel che questo significa in concreto, basti pensare che possiamo ottenere il valore di c – 2 = 0,9979246 non da uno solo, ma da quei due valori che vediamo qui sotto (si noti come la seconda cifra è vicinissima a (3 + 1/ɸ_Cheope )/10³ = 0,003617821..)

0,99506743691.. ! = c – 2 = 0,9979246

0,0036178905.. ! = c – 2 = 0,9979246

La cifra che rappresenta il limite entro il quale il prodotto fattoriale diminuisce al diminuire del numero di partenza è un numero irrazionale, che si trova in un intervallo compreso nelle cifre che seguono.

Nel caso della prima cifra, vediamo che la differenza fra i due prodotti fattoriali è positiva: dunque, a questo punto, diminuendo la cifra il prodotto fattoriale è ancora in fase di decrescita con il decrescere del numero

0,46163214497.. ! – 0,4616321449699.. ! = 1,3605816740556638879314578940543 ∙ 10^-25

Qui sotto la differenza fra i due prodotti fattoriali è negativa, per quanto il primo numero sia maggiore del secondo: dunque, a questo punto, diminuendo la cifra il prodotto fattoriale è entrato nella fase in cui cresce con il decrescere del numero

0,461632144968.. ! – 0,4616321449679..! = -3,5336558936577958643380000953587 ∙ 10^-26

Ne viene di conseguenza che il prodotto fattoriale minimo che si può ottenere da numeri tali per cui 1 ≥ x ≥ 0 è quello di una cifra che si trova fra 0,46163214497 e 0,461632144968. Una sua discreta approssimazione è quella che vediamo qui sotto, di cui possiamo ottenere una discreta approssimazione per mezzo di e^√π

0,46163214497.. ! = 0,88560319441.. ≈ e^√π – 5 = 0,88527725..

Siccome il prodotto fattoriale minimo che si può ottenere da numeri compresi fra 1 ≥ x ≥ 0 sembra in assoluto il più piccolo, anche se consideriamo i numeri negativi, a volte per brevità esprimeremo la sua base, che è quella di cui ci occuperemo maggiormente, con il simbolo BM (!). Invece, con il simbolo min (!) esprimeremo il suo prodotto fattoriale. Dunque

BM (!) = 0,46163214497.. !

min (!) = 0,88560319441..

2.

Quanto a quello che potremmo definire come il “significato armonico” di questo numero, ovvero la sua capacità di entrare in una rete di relazioni significative con altri numeri importanti del sistema matematico che descrive l’universo, la cosa più evidente è che possiamo dedurlo da uno dei valori sperimentalmente possibili del numero caratteristico della lunghezza di Planck ℓ_P = 1,616258.. Infatti, scegliendo l’approssimazione che vediamo qui sotto, aggiungendo 3 e dividendo per 10, possiamo ottenere il limite in questione

(3 + 1,6163214497.. )/10 = 0,46163214497..

Se andiamo a vedere il seno che corrisponde a BM (!) vediamo che è quello di un angolo il cui coseno risulta una funzione approssimata di π

sen x = BM (!) = 0,46163214497..

x = 27°,492477..

[2 ∙ (cos 27°,492477..)]² = [2 ∙ 0,887071..]² = 1,774142906..² = 3,147583.. ≈ π = 3,141592..

Inoltre, BM (!) ha altri rapporti con costanti scientifiche di rilievo. In primo luogo, se lo dividiamo per il suo prodotto fattoriale e lo moltiplichiamo per 4π, quello che otteniamo è il valore del numero caratteristico della costante di Planck così come fu calcolato da Planck stesso all’inizio del secolo scorso h_Planck = 6,55. E, come abbiamo visto a partire da The Snefru Code parte 9, questo valore può essere considerato il margine di oscillazione minimo di h.

4 π ∙ [BM (!) : min (!)]= 4 π ∙ (0,46163214497.. : 0,88560319441..) =

4 π ∙ 0,521262962.. = 6,550383.. ≈ h_Planck = 6,55

Questo fatto può essere considerato altamente simbolico, dato che il prodotto fattoriale di 0,46163214497 è il minimo che possiamo ottenere fra tutti i numeri tali per cui 1 ≥ x ≥ 0: e 6,55 rappresenta invece la minima quantità possibile dell’unità energetica al di sotto della quale non si può scendere senza che la trasmissione di energia rimanga zero.

Si noti anche che 0,521262962.., moltiplicato per 10² e diviso per l’angolo giro, va molto vicino a quell’angolo che, diviso per 360, ci dà Ln π – 1

(0,521262962.. ∙ 10²) : 360 = 0,1447952672.. ≈ Ln π – 1 = 52,102758.. : 360 = 0,144729885..

Per altro verso, facendo l’inverso del logaritmo naturale di -1/0,46163214497.. e moltiplicandolo per 10³ otteniamo di un valore molto prossimo a 360°/π. L’approssimazione di π che possiamo ottenerne differisce dal valore esatto di circa 5 decimillesimi

360 : (e^{-1/0,46163214497..} ∙ 10³) = 360 : (e^{-2,166226964..} ∙ 10³) = 360 : 114,609226.. = 3,141108.. ≈ π = 3,141592..

D’altra parte, a partire da e^{-1/0,46163214497..} possiamo arrivare a una discreta approssimazione di π anche in quest’altro modo

inv. Ln (e^{-1/0,46163214497..} ∙ 10) = inv. Ln (e^{-2,166226964..} ∙ 10) = e^{1,146092268..} = 3,145875..

Inoltre, a livello trigonometrico, BM (!) ha un’altra connessione piuttosto complessa con π. Se prendiamo BM (!) come un seno, e ricaviamo l’angolo, poi min (!) come un coseno, e di nuovo ricaviamo l’angolo, vediamo che il prodotto fattoriale della differenza fra i due angoli è una buona approssimazione di Ln π

sen x = BM (!); x = 27°,492477079472522274210907805391

cos y = min (!); y = 27°,674157759640971585519529241547

(x – y) ! = (27°,492477.. – 27°,674157..) ! = -0,181680..! = 1,144265.. ≈ Ln π = 1,144729..

Queste connessioni della BM (!) con π vedono enormemente rafforzato il loro significato dal fatto che il suo logaritmo naturale, proprio come la sua radice cubica, ci danno due ottime approssimazioni di √π – 1, anche se di segno opposto

(Ln 0,46163214497..) – 1 = -0,772986928.. – 1 = -1,772986928.. ≈ -√π = -1,7724538509..

1 + ³√0,46163214497.. = 1 + 0,772856174.. – 1 = 1,772856174.. ≈ √π = 1,7724538509..

E qui sembra davvero molto importante notare che possiamo ottenere un’approssimazione di √π e dunque di π che sfiora la perfezione assoluta a partire da un numero molto particolare, ovvero da -1/2, che è il coseno dell’angolo di 60°, come anche il seno di quello di 30°: questi angoli sono rispettivamente 1/6 e 1/12 dell’angolo giro: il che ci permette di comprendere una volta di più le ragioni profonde, matematico-scientifiche della sacralizzazione di questi numeri. Si noti anche che dalla tangente di 60°, e sempre per mezzo del prodotto fattoriale, possiamo ottenere un’ottima approssimazione del numero caratteristico della costante che descrive la carica unitaria di protone ed elettrone come anche di √2

-(-tg 60°! ) – tg² 60°= – (-1,732050.. !) – 3 = 4,60296.. – 3 = 1,60296.. ≈ c_u = 1,6022

tg² 60°- tg 60°! = 3 – 1,732050..! = 3 – 1,585003.. = 1,414996.. ≈ √2 = 1,414213..

Da quest’approssimazione di √2 possiamo a sua volta ottenere un’ottima approssimazione di π con un’operazione che oramai ci sarà diventata consueta

₃inv. Ln -(1,414213..²) = ₃inv. Ln -2,002214606.. = 3,141115.. ≈ π = 3,141592..

L’angolo la cui tangente è pari a 1/2 è quello di 26°,565051.. e anche quest’angolo, al di là delle apparenze un po’ anonime, si connette profondamente con π. Lo possiamo scoprire dividendo dapprima l’angolo giro per questo angolo

360° : 26°,565051.. = 13,551639618546296181803494355291..

Se adesso facciamo la sottrazione fra l’angolo di 26°,565051.. e il risultato che abbiamo appena ottenuto arriviamo un numero molto vicino a 13. Se con questo numero facciamo 1/x^x, possiamo arrivare a una discreta approssimazione π

26,565051.. – 13,551639.. = 13,0134115..

1/13,013411..^13,013411.. = 1/317709986249943,850.. = 3,147524.. ∙ 10^-15

Escludendo la potenza di 10, quest’approssimazione di π è particolarmente vicina a quella che abbiamo ottenuto sopra a partire da BM (!) inteso numerologicamente come un seno

sen x = BM (!) = 0,46163214497..

x = 27°,492477..

[2 ∙ (cos 27°,492477..)]² = 3,147583.. ≈ 1/13,013411..^13,013411.. = 3,147524..

A livello trigonometrico, il valore di 1/2 deve avere un significato speciale, perché se andiamo a vedere, anche l’angolo pari a 1/2 si connette a π. Infatti, se dividiamo l’angolo giro per l’inverso della sua tangente, otteniamo di nuovo un’ottima approssimazione di π

360°: 1/tg1/2 = 360° : 1/0,008726867.. = 360° : 114,588650.. = 3,141672.. ≈ π = 3,141592..

Se poi prendiamo -1/2 e lo dividiamo per 10 otteniamo 1/20 (che corrisponde all’inverso di un mese Maya di 20 giorni). Se facciamo il prodotto fattoriale di -1/20 = 0,05, anche in questo modo otteniamo una connessione con π

-1/20 ! = 1,031453317.. ≈ 1 + π/10² = 1,0314159265..

3.

La differenza fra il valore approssimato di π che possiamo ottenere da -1/2! e quello effettivo è piccolissima. Talmente piccola che può darsi che la calcolatrice di Windows non riesca ad afferrarla bene. Comunque sia, la differenza che in ogni caso segnala, se corrispondesse a realtà, non sembra di importanza minore, dato che corrisponde al valore assoluto della costante di Dirac moltiplicato per 10

(-1/2 !)² = 1,772453850905..² = 3,1415926535897932384626433832795.. ≈ π (-1,054677.. ∙ 10^-33 ≈

≈ ħ ∙ 10 = 1,054571.. ∙ 10^-34 ∙ 10 = 1,054571.. ∙ 10^-33

Né sembra meno significativo il fatto che sia il prodotto fattoriale di -1/G che quello di -1/h producano delle buone approssimazioni della costante di Dirac elevata al quadrato, con -1/G che arriva a sfiorare la perfezione

-1/G ! = -1/6,672 ! = -0,149880095..! = 1,112369673.. ≈ ħ² = 1,112121318..

-1/h ! = -1/6,626 ! = -0,150920615..! = 1,113361013.. ≈ ħ² = 1,112121318..

E qui sembra importante segnalare che l’approssimazione di ħ che possiamo ricavare da -1/h !, sebbene sia leggermente più imprecisa, differisce di pochissimo dall’inverso del coseno di quell’angolo x in grado di soddisfare l’equazione armonica che vediamo qui sotto

x = -cos x ! x = 18°,6058009269..

1/cos 18°,6058009269.. = 1/0,9477361120291.. = 1,055146034.. ≈ √-1/h ! = 1,055159235..

Per quanto riguarda il lavoro che stiamo svolgendo, c’è un’altra cosa importantissima da notare sui prodotti fattoriali di numeri compresi fra 0 ≥ x ≥ -1. Se prendiamo una costante atomica qualsiasi – il cui valore è molto piccolo, e gli sottraiamo 1, vediamo che il prodotto fattoriale del risultato è quasi identico al suo inverso: il che contribuisce alla costruzione di quel sistema in cui “tutto è connesso con tutto” che l’universo sembra, ove conosciuto attraverso questa meravigliosa forma della matematica. In questo caso, si crea una connessione fra la costante fisica e il numero dal cui prodotto fattoriale si può ricavare il suo inverso. Prendiamo per esempio la massa e il raggio classico del protone

m_p – 1 != 1,6725 ∙ 10^-27 – 1 ! = -0,9999999999999999999999999983275.. ! =

= 597907324364722384965977981,36561 = 1/1,6725 ∙ 10^-27

r_p – 1 ! = 1,535 ∙ 10^-18 – 1 ! = -0,999999999999999998465 ! =

651465798045602605,28597651750889 = 1,535 ∙ 10^-18

Ma ben più importante di questo sembra il fatto che se prendiamo quel numero compreso fra 0 ≥ x ≥ -1 il cui prodotto fattoriale è pari a 360, vediamo che l’inverso della sua radice è pari al rapporto fra la massa del neutrone e quella del protone

-0,997226647873..! = 360

1,6725 ∙ 1/√0,997226647873.. = 1,6725 ∙ 1/0,998623223.. = 1,6725 ∙ 1,001378674.. = m_n = 1,6748

Già a questo punto, possiamo dire che un’operazione come il prodotto fattoriale, fondata sulla scomposizione del numero nelle sue parti, conferma la nostra ipotesi di fondo: ovvero che ogni singolo va inteso non come un punto sull’asse cartesiano, ma come una struttura complessa, una microstruttura potremmo dire, che non senza ragione abbiamo paragonato a quella di un neurone. Nell’ambito di questa microstruttura si ritrovano quelle stesse connessioni con altri numeri significativi che abbiamo già individuato a livello – diciamo così di macrostruttura. Ogni singolo numero sarebbe, in questa concezione, una sorta di microcosmo in cui si riflette il macrocosmo, cioè il mondo dei numeri nel suo complesso.

Ma naturalmente, la nostra analisi è solo all’inizio. Le prove di un’affermazione così importante infatti non possono essere tanto esigue come quelle che abbiamo presentato fino ad adesso. Per aggiungerne, altre possiamo per prima cosa un fatto molto importante: ovvero che sono legate a un’approssimazione di -π²/10 = 0,986960.. anche quei numeri il cui prodotto fattoriale rimanda ad angoli dotati di caratteristiche estremamente significative, quali quello di 72° e quelli vicini che hanno per tangente π e c = 2,9979246

-0,9862190153233.. ! = 72°

-0,9862839017073.. ! = 72°,343212848..; tg 72°,3432.. = π

-0,9861336103946..! = 71°,553152602..; tg 71°,553152.. = c = 2,9979246..

Dato quel che abbiamo appena visto sopra, diventa quasi banale notare che l’angolo x in grado di soddisfare l’equazione armonica che vediamo qui di seguito ha una tangente molto vicina π

x = -(tg² x)/10 !

x = 72°,33752539386491..

tg x = 3,14051402073138..

-(tg² x)/10 = -0,98628283144104051..

-0,98628283144104051..! = 72,33752539386491..

4.

Questi legami fra le approssimazioni di -π²/10 e angoli con tangenti connesse con valori molto importanti, fra cui anche quello con tangente pari a π, vedono ampliato e insieme rafforzato il loro significato sistemico quando ci rendiamo conto che aggiungendo 9 a π²/10 e facendo per 3 volte il logaritmo naturale, arriviamo a un numero negativo che risulta essere la base fattoriale di un numero vicinissimo al logaritmo naturale di π

₃Ln [(3² + π²/10)] ! = [₃Ln (9 + 0,986960..)] ! = (₃Ln 9,986960..)! =

= -0,182162..! = 1,144775.. ≈ Ln π = 1,144729..

Se eleviamo questo numero al cubo e poi facciamo il logaritmo in base 10, il risultato che otteniamo va piuttosto vicino al valore di c = 2,9979246

log 9,98696044..³ = log 996,093230.. = 2,9982999.. ≈ c = 2,9979246

Aggiungere 3² = 9 a π²/10, sul momento, potrebbe sembrare un’operazione del tutto arbitraria. Ma, in realtà quest’operazione si colloca in un contesto che sembra giustificarla pienamente. Oltre al fatto che il 3, come abbiamo visto, è un trait d’union privilegiato fra π e ɸ – dato che da 3/ɸ possiamo ricavare un’approssimazione di π che differisce dal valore esatto di pochi milionesimi – possiamo anche notare che 9 più π² corrisponde a un’ottima approssimazione del coseno di π moltiplicato per 10

(₃Ln cos π ∙ 10) ! = (₃Ln 9,984971498..) ! = -0,18226668.. ! = 1,144885.. ≈ Ln π = 1,144729..

log 9,984971498..³ = log 995,498221.. = 2,998040488.. ≈ c = 2,9979246

Inoltre, un valore molto simile a questo corrisponde all’inverso dell’angolo che ha una tangente iperbolica pari a (c – 2)/10

tanh x = (c – 2)/10 = 0,09979246

x = 0°,100125715..

1/0,100125715.. = 9,987444208.. ≈ 3² + π²/10 = 9,986960..

Perfino quel numero il cui prodotto fattoriale è uguale a 1 più il numero stesso moltiplicato per -1 è un numero connesso con π. Si noti che, se interpretato numerologicamente come un coseno, esso corrisponde a un angolo la cui tangente è di nuovo molto vicina a π

-x ! = 1 + x = 1,3032799071..

x = -0,30327990715..

₂inv. log -0,30327990715.. = 3,14352118.. ≈ π = 3,141592653..

cos y = 0,30327990715..

y = 72°,345291108..

tg 72°,345291108.. = 3,141986.. π = 3,141592..

Lo stesso vale per quella x tale per cui 1/x – x = 3

3,3027756377319946465596106337352 – 1/3,3027756377319946465596106337352 = 3

₂inv. log -0,302775637.. = 3,147706921.. ≈ π = 3,141592653..

Un valore molto prossimo a π si connette anche all’equazione armonica che vediamo qui sotto, in cui vediamo che il prodotto fattoriale di x diviso per il doppio del suo logaritmo naturale è ancora una volta molto vicino a π. Si noti che il valore della differenza con il valore esatto di π è una funzione molto ben approssimata di ɸ:

x! : (Ln x)/2 = x = 3,142481.. ≈ π = 3,141592.. (+8,883736118.. ∙ 10^-4 ≈ (2/ɸ)³ – 1 ∙ 10^-3 = 8,88543819.. ∙ 10^-4

Un’approssimazione di ɸ praticamente perfetta la possiamo ricavare anche dal prodotto fattoriale di π. E, per mezzo del prodotto fattoriale di π e del 3, possiamo creare una sorta di cerchio magico matematico, con cui torniamo di nuovo al valore di partenza, π, con una leggera approssimazione per difetto

-(π! – 3π) = 2,2366952317933470133057358047137 ≈ ɸ + 1/ɸ = 2,2360679774997896964091736687313

₃inv. Ln -(π! – 3π)² + 3 = ₃inv. Ln -5,002805.. + 3 = ₃inv. Ln -2,00280555.. = 3,1408283..

Per finire, possiamo notare che da relazioni – diciamo a così – interne a π viene fuori anche un valore scientifico molto importante, vale a dire il numero caratteristico raggio classico del protone. Un valore che però subito dopo scopriamo di poter derivare anche da una funzione del seno iperbolico del numero di Eulero

1/(π! ∙ tg π) – 1 = 1/(7,188082.. ∙ 0,0548861..) – 1 = 1/0,394526.. – 1 = 2,534685.. – 1 = 1,534685.. ≈ r_p = 1,535

¹⁶√₂sinh e = ¹²√944,815473416.. = 1,534472.. ≈ r_p = 1,535

Questo valore possiamo ricavarlo in modo ancor meglio approssimato da questa strana funzione di π e ɸ

√log 1/{ɸ! – [1 + [π ∙ (π – 3)]} = √log 1/0,004403.. = √log 227,109.. =

= √2,356235340735.. = 1,535003.. ≈ r_p = 1,535

E qui sembra che ci troviamo di nuovo di fronte a un numero che sembra avere un senso anche come sequenza. Se prendiamo 2,356235340735.. e gli togliamo le prime 4 cifre, e poi lo moltiplichiamo per 10⁴, facendo ancora una volta la radice quel che viene fuori è un’altra volta il raggio del protone

√[(2,356235340735.. – 2,356) ∙ 10⁴] = √2,35340735.. = 1,534081.. ≈ r_p = 1,535

Una cosa simile accade anche con ɸ. Se gli togliamo le prime 4 cifre e poi facciamo l’inverso, facendo la radice otteniamo una discreta approssimazione di 1 + ɸ²

⁸√1/(1,61803398874989484820458683436 – 1,618) = ⁸√129421,499851.. = 3,618954.. ≈ 1 + ɸ² = 3,618033..

Se togliamo le prime 7 cifre, possiamo poi trovare una discreta approssimazione di h = 6,626

₂Ln 1/(1,61803398874989484820458683436 – 1,618033..) = 2,626610.. ≈ h – 4 = 2,626

log 1/(1,61803398874989484820458683436 – 1,618033..) = 6,00491.. ≈ 6

Riconosciamo che in questo caso le prove che portiamo a fondamento della nostra ipotesi sono scarse. Però, quel che pare di poter intuire su questo pur scarso fondamento, è che per la comprensione di cosa sia un numero come ɸ, o come π, o come il numero di Eulero occorre far ricorso al concetto di sequenza di numeri costitutivi. Facendo in questo modo, in The Snefru Code Parte 12, ci siamo resi conto che il 10 è connesso con ɸ e con π. Infatti, scrivendo in sequenza normale e inversa i numeri da 1 a 9 e ponendo la virgola dietro il primo membro della serie, ottenevamo in un caso un’approssimazione di 2/ɸ, nell’altro una di π²

1,23456789.. ≈ 2/ɸ = 1,23606797..

9,87654321.. ≈ π² = 9,8696044..

Analizzare questo problema non è però il compito di questo scritto. Lo svolgeremo meglio in un lavoro successivo.

5.

Osservando tutte queste connessioni organiche fra numeri che hanno una molteplicità di significati di grande rilevanza si fa fatica a conservare quello scetticismo a cui pure la nostra epoca ci ha educati e che comunque sia è indispensabile per conservare quella distanza critica che è indispensabile alla ricerca scientifica. Ad ogni passo che facciamo avanti nella nostra analisi, il mondo del numero sembra svelarsi sempre di più come un sistema interconnesso, intelligente, del tutto simile al cervello. Il nostro cervello infatti, pur basato su dei mattoni biologici che, in apparenza, sembrano tutti uguali, che a loro volta sembrano compiere un ben misero lavoro matematico, che si risolve nella scelta fra un’alternativa binaria, attraverso la complessità delle loro interconnessioni sono capaci di dar luogo a un’intelligenza capace di contemplare l’universo ai livelli più diversi: artistico, filosofico, mistico, e scientifico matematico. E, analizzando il mondo dei numeri, sempre più spontaneo viene il pensiero che il sistema delle interconnessioni neuronali debba essere uno specchio delle interconnessioni fra i numeri, che a loro volta sono lo specchio dell’intelligenza divina, che percorre tutto l’universo, materiale e spirituale, infinitamente grande e infinitamente piccolo.

L’ipotesi sembra azzardata, e forse lo è davvero. D’altra parte, dopo aver visto tutti quegli angoli significativi, fra cui anche quello di 72°, si legano ad approssimazioni di -π²/10 , adesso scopriamo che un valore pressoché identico alla tangente dell’angolo di 72° possiamo ottenerla da -1/√10 nel modo che vediamo qui sotto

1/(-1/√10 !)⁴ = 1,324510983..⁴ = 3,077671455.. ≈ tg 72° = 3,077683537..

Oppure, quando andiamo a vedere quale sia quel numero capace di soddisfare l’equazione armonica che vediamo qui sotto, dapprima scopriamo che è vicinissimo a 2 (una cosa già di per sé significativa)

(₂Ln x !)² = x x = 2,001606698888972..

A ciò si aggiunge il fatto che questo numero, e dunque anche il 2, sono connessi sia con la durata dell’anno delle fasi lunari (354,36 giorni) e sia con quella dell’anno delle eclissi (346,6 giorni)

₂Ln 2,001606698888972.. = -0,365355.. ≈ 365,25/-10³ = 0,365,25 ≈ ₂Ln 2 = 0,366512..

Ln (₂Ln x !) 2,001606698888972.. = 0,346975.. ≈ Ln √2 = 0,346573.. ≈ 346,6/10³ = 0,3466

L’impressione che l’universo sia una un ritmo di tempi, spazi e misure regolate da un ritmo sacro, da quella che i pitagorici chiamavano “armonia delle sfere”, si rafforza quando scopriamo che al 2 e a √2 si connettono tanto il numero caratteristico del raggio che quello del diametro classico del protone

√[2 + (1/√2)/2] = √2,353553.. = 1,534129.. ≈ r_p = 1,535

-1/√2 ! = 3,067931.. ≈ d_p = 3,07

6.

Il lettore ci perdoni per questo lungo inciso, che sul momento può sembrare anche una mera distrazione espositiva da quello che era l’argomento che stavamo trattando, ovvero la base del prodotto fattoriale minimo BM (!) = 0,4616.. . Ma qui sembrava davvero molto importante sottolineare questo particolare “momento armonico” del prodotto fattoriale, che inserito in altri contesti poteva apparire meno pregnante, meno significativo. Le deviazioni che di volta in volta facciamo da un argomento verso le sue ramificazioni, al contrario di quanto può sembrare, non sono delle “distrazioni”. Esse vengono rese necessarie dalla natura complessa dell’argomento trattato: le infinite ramificazioni e le meravigliose circolarità del sistema matematico che stiamo tanto faticosamente esplorando ci rendono impossibile un’esposizione lineare, anche al di là delle limitate capacità o addirittura delle intenzioni di chi si trova a esporlo.

Qui non abbiamo a che fare con la matematica a cui siamo abituati a partire da liceo: essa non e come una piramide dalla cui base si procede con sicurezza verso la cuspide. viceversa, la cuspide di questa strana piramide, che abbiamo più volte paragonato alla sfera di Ermete Trismegisto, è già punto della sua base. È per questo che abbiamo potuto scrivere che “il sapere è come una piramide la cui cuspide è ovunque e la cui base è da nessuna parte”.

Ogni parte si connette con l’altra ininterrottamente. È come quella tunica senza cuciture che i legionari si spartiscono ai piedi della Croce, che altro non rappresenta che la sapienza divina di cui Gesù, in quanto Figlio di Dio, era possessore e di cui i miracoli erano la testimonianza più eclatante. Nella mitologia norrena troviamo che Orvandill, il padre dell’Amlethus di Saxo, “durante un viaggio fa naufragio, trova rifugio presso un mastro pescatore di nome Esen, si guadagna l’abito senza cuciture“. Anche in questa mitologia Amlethus, il personaggio principale è legato a Saturno, il fabbro che forgia l’universo secondo numero e misura. Ma anche Amlethus (e dunque, c’è da presumerlo, anche il padre) è possessore di un sapere profondo, dissimulato in un’apparente follia che è diventata familiare agli intellettuali occidentali per mezzo del personaggio di Amleto. Ma il sapere matematico con cui abbiamo a che fare sembra proprio questo, una tunica senza cuciture: un sapere antichissimo dunque, ermetico, di cui nel mito non si trova la pienezza, ma sole le allusioni. Un sapere che però è a fondamento di quella geometria sacra che è stata usata per costruire la Piramide.

Per fare un altro esempio, che ci possa chiarire cosa sia quest’abito senza cuciture, se c’è un valore che sul momento ci può sembrare del tutto estraneo all’argomento che stiamo trattando è la differenza fra π e c = 2,9979246. In effetti, la velocità della luce non sembrava avere nulla a che fare con le equazioni che stavamo esponendo. E invece, se diamo un’occhiata alle equazioni che vediamo qui sotto scopriamo immediatamente che non solo il nesso esiste, ma che ha un significato epistemologicamente incalcolabile dato che, proiettata attraverso la trigonometria sui prodotti fattoriali di numeri compresi fra 0 ≥ x ≥ -1, essa rivela delle insospettabili connessioni con π, che sono quelle che abbiamo trattato alla fine del paragrafo precedente. Infatti il coseno di un angolo pari a π – c non è altro che la base fattoriale di un multiplo di 1/π

x = π – c = 0°,1436680535897932384626433832795

cos 0,143668.. = 0,99999685627225506128287771465264

-0,999996856272..! = 318093,125911.. ≈ 10⁶/π = 318309,886183..

Similmente, esiste un angolo da cui possiamo ottenere la velocità della luce a partire dal coseno

cos 0°,0147988264.. = 0,99999996664359114587808187218594

-0,99999996664359.. ! = 29979245,821.. = c

Ebbene, questo angolo si connette con la costante di Planck perché la sua radice nona è un valore con cui oramai abbiamo acquistato una certa familiarità, ovvero h – 6

⁹√0°,0147988264.. = 0,626169.. ≈ h – 6 = 0,626

7.

Dunque a questo punto, le connessioni della base del minimo prodotto fattoriale BM (!) = 0,46163214497 con √π – 1 risultano enormemente arricchite di significato, dato che il prodotto fattoriale di numeri variamente connessi con π ci consente di ottenere una gran quantità di dati scientifici armonicamente connessi. E, nel prosieguo dell’analisi, scopriremo che tali connessioni si ampliano ancor di più, fino a toccare la totalità del sistema matematico di cui fanno parte.

Infatti se adesso andiamo a rivedere che le due approssimazioni di √π – 1 che avevamo calcolato, pur molto simili, hanno però una piccolo differenza

(Ln 0,46163214497..) – 1 = -0,772986928.. – 1 = -1,772986928.. ≈ -√π = -1,7724538509..

1 + ³√0,46163214497.. = 1 + 0,772856174.. – 1 = 1,772856174.. ≈ √π = 1,7724538509..

Ebbene, se adesso dividiamo l’angolo giro per la radice della differenza fra le due approssimazioni moltiplicata questa volta per 10⁴, otteniamo ancora una volta una buona approssimazione di π

360 : [√(0,772986928.. – 0,772856174..) ∙ 10⁴ = 360 : (√0,000130754.. ∙ 10⁴) =

= 360 : 114,347715.. = 3,148292.. ≈ π = 3,141592..

Inoltre, il fatto che le due approssimazioni di √π – 1 che abbiamo ricavato da BM (!) siano tanto vicine ci fa capire che tanto BM (!) che √π – 1 sono entrambi legati alla x in grado di soddisfare l’equazione armonica che vediamo qui sotto, connessa con quel numero la cui radice cubica, sottratta al suo logaritmo, è uguale a 0

³√x + Ln x = 0

x = 0,46168014285.. ≈ BM (!) = 0,46163214497.. ≈ (√π – 1)³ = 0,460911588..

Dobbiamo inoltre notare che BM (!) ha un altro genere di legame con π, che passa però per il numero di Eulero. Infatti se eleviamo al quadrato il prodotto fattoriale di -BM (!) = –0,46163214497.. otteniamo un numero molto vicino a e. Ma se facciamo il doppio logaritmo naturale dell’inverso della differenza, il valore che otteniamo differisce da √π di circa un decimillesimo

-0,46163214497.. ! = 2,721063.. ≈ e = 2,718281.. (+0,00278163747355820834471830867383

₂Ln 1/0,002781637.. = ₂Ln 359,500477.. = 1,772358.. ≈ √π = 1,772453..( -9,545368.. ∙ 10^-5

A sua volta, la radice ottava dell’inverso di questa differenza equivale a un valore molto prossimo a 10/π

⁸√1/9,545368.. ∙ 10^-5 = ⁸√10476,285461.. = 3,180723.. ≈ 10/π = 3,183098..

E qui sarà bene soffermarsi a notare che BM (!) ha una relazione molto interessante con un altro di quelli che possiamo definire “numeri armonici”. Infatti, se facciamo il prodotto fra quel numero la cui radice cubica è uguale alla sua metà – che sarebbe √8 = (√2)³ – e il numero di Eulero, scopriamo che la radice del risultato è simile a quell’approssimazione di √π che abbiamo appena ricavato: solo, invece di aggiungere 1, questa volta dobbiamo sottrarre 1

√[(√2)³ ∙ e] = √(2,828427.. ∙ 2,718281..) = √7,688462.. = 2,772807612.. ≈ √π + 1 = 2,7724538509..

Essendo queste approssimazioni di √π tanto vicine, ciò significa che da 0,46163214497.. possiamo facilmente ricavare un’ottima approssimazione del numero di Eulero nel modo che vediamo qui sotto

(³√0,46163214497.. + 2)² : (√2)³ = 2,718377042.. ≈ e = 2,71828182.. (+9,521450587.. ∙ 10^-5

Curiosamente, l’inverso della differenze corrisponde all’anno in cui le 3 Piramidi di Giza corrispondevano con la disposizione delle tre stelle della Cintura di Orione, il 10500 a.C. circa. La radice ottava di questa cifra non è altro che 10/π_Cheope

⁸√1/9,521450587.. ∙ 10^-5 = ⁸√10502,601371.. = 3,181721.. ≈ 10/π_Cheope = 3,181818..

8.

Quindi, a quel che sembra BM (!) ha un legame molto articolato e complesso con π, a cui dobbiamo aggiungere sia quello con la costante di Planck che quello con la lunghezza di Planck. Ma, come abbiamo visto in precedenza, numeri significativi, capaci di stabilire questo genere di relazioni complesse con altri numeri a vario titolo significativi, non sono dei punti isolati, ma hanno vicino a sé dei numeri che a loro volta presentano caratteristiche particolari. E, anche in questo caso, molto vicino a BM (!) ne abbiamo trovato uno che stabilisce una simmetria matematica particolare, ovvero quel numero la cui radice cubica, sommata al suo logaritmo naturale, è uguale a 0. Quindi, anche questo numero è in stretto rapporto sia con la costante di Planck, che con la lunghezza di Planck, sia con π. Siamo quindi in presenza di un intorno matematico che sembra della massima rilevanza.

Ma, come ci apprestiamo a vedere, il suo significato matematico non si esaurisce nemmeno a questo pur elevato livello di complessità. Infatti, come prima cosa, possiamo notare che se dividiamo 0,46163214497.. per il suo logaritmo naturale, otteniamo l’inverso del numero caratteristico della massa del protone m_n = 1,6748

-1/(0,46163214497.. : Ln 0,46163214497..) = -1/(0,46163214497.. : Ln -0,772986928..) =

= -1/-0,597205629.. = 1,674465.. ≈ m_n = 1,6748

Invece, l’inverso del logaritmo di 0,46163214497.. corrisponde alla metà della radice di un numero che risulta da una funzione di c: un po’ complicata, è vero, ma pur sempre una funzione di c

(2 ∙ e^{0,46163214497..})² = 10,069979299.. ≈ 10 + (4 + c)/10² = 10,069979246

Se adesso facciamo l’inverso del logaritmo in base 10 del risultato della moltiplicazione di 0,46163214497.. con il suo prodotto fattoriale, passiamo dalla velocità della luce alla sua fonte più importante per l’essere umano, dato che otteniamo un’ottima approssimazione della durata dell’anno solare

0,46163214497.. ! ∙ 0,46163214497.. = 0,88560319.. ∙ 0,46163214497.. = 0,408822902..

₂inv. log 0,408822902.. = 365,964.. ≈ 365,25

Se adesso andiamo a controllare una ramificazione trigonometrica di 0,46163214497.. equivale a circa un decimo della tangente di un angolo molto particolare. Stiamo parlando della tangente di quell’angolo la cui tangente equivale all’angolo giro diviso per il valore dell’angolo stesso, ovvero alla x in grado di soddisfare l’equazione armonica che vediamo qui sotto

tg x = 360 : x = 4,6269765532463866775379620929775 ≈ 0,46163214497.. ∙ 10 = 4,616321

x = 77°,804587046678726988646504245797

La tangente di 77°,804.. è a sua volta molto vicina alla x in grado di soddisfare l’equazione armonica che vediamo qui sotto, il cui logaritmo in base 10 è 2/3, cioè una di quelle cifre cui molto probabilmente allude il Numero della Bestia

x : 1/√x = 10; x = 4,6415888336127788924100763509194;

log 4,6415888336127788924100763509194 = 2/3 = 0,666666..

Di nuovo troviamo che due numeri significativi sono legati fra di loro da qualcosa come un ritmo matematico particolare. Infatti, la radice quarta della differenza fra questi due numeri armonici che abbiamo appena trovato, se moltiplicata per 10 ci dà un’ottima approssimazione di 1/ɸ

⁴√[(4,641588.. – 4,626976..) ∙ 10] = ⁴√0,146122803.. = 0,618271.. ≈ 1/ɸ = 0,618033..

9.

Quindi, BM (!), come altri numeri importanti della matematica, è caratterizzato da una serie di relazioni significative, che lo mettono, per così dire, in rete con molte grandezze significative sia per la fisica che per la matematica. All’inizio di questa indagine ci eravamo resi conto che esso può essere ricavato aggiungendo 3 a un’approssimazione sperimentalmente possibile della lunghezza di Planck e poi dividendola per 10. Adesso ci apprestiamo a scoprire che questo numero si lega a questa stessa grandezza fisica anche per un’altra via. Infatti, vediamo che la sua radice specchio negativa si connette con un’altra approssimazione di ℓ_P – 1

⁸√(^{-0,46163214497..}√0,46163214497..) : 2 = ⁸√5,335940333.. : 2 = 1,232824.. : 2 = 0,616412.. ≈ ℓ_P – 1 = 0,616252..

Questo particolare tipo di rapporto fra 0,46163214497..e la lunghezza di Planck ci dà l’occasione di notare una relazione di tipo un po’ più complesso che questo numero intrattiene con il raggio classico del protone. Lo possiamo scoprire a partire dall’equazione che vediamo qui sotto, in cui scopriamo che la differenza fra 2 e ⁸√(^{-0,46163214497..}√0,46163214497..) = 1,232824.. corrisponde appunto alla metà di questo valore fisico. Infatti

[2 – ⁸√(^{-0,46163214497..}√0,46163214497..)] ∙ -2 = (2 – 1,232824823..) ∙ -2 =

= -0,767175176.. ∙ -2 = 1,534350.. ≈ r_p = 1,535

Questa relazione, lo riconosciamo, sul momento può sembrare, oltre che eccessivamente complicata, anche un po’ arbitraria. Però questa impressione tende a svanire quando ci rendiamo conto che, scegliendo un valore del raggio classico del protone che rientra fa quelli resi possibili dal principio di indeterminazione, vediamo che la differenza con il suo inverso corrisponde esattamente al prodotto fattoriale di 0,46163214497.., ovvero al prodotto fattoriale minimo che possiamo ottenere da un numero positivo. Il che, di nuovo ci mostra in modo inequivocabile che, davvero, la matematica di essa è davvero paragonabile a una tunica senza cuciture: visto attraverso di essa, l’universo non ci appare più come una somma di particolari caotici, ma come un meraviglioso sistema di simmetrie armoniche infinitamente interconnesse

1,53645293766.. – 1/1,53645293766.. = 0,88560319441.. = 0,46163214497..!

Una nuova prova di questa affermazione la scopriamo quando ci rendiamo conto che anche l’inverso di 0,46163214497.. corrisponde alla tangente di un angolo di nuovo un po’ particolare, perché, di nuovo, il suo coseno risulta da un funzione approssimata di ɸ_Cheope. Ed è forse inutile a questo punto far notare l’enorme importanza che il numero d’oro sta assumendo sempre più nella nostra ricerca. A quel che sembra, esso fu codificato dagli Antichi Egizi in modo approssimato proprio per indicare che – a partire da un intorno numerico situato intorno al valore esatto di ɸ – si possono dedurre tutti i numeri e i rapporti fondamentali che reggono regolano l’universo (ma lo stesso ovviamente vale anche per π e per l’approssimazione codificata nella Piramide, pari al numero di Pitagora 22/7).

tg x = 1/0,46163214497.. = 2,1662269642530781926540066783686

x = 65°,220434538049683305955023191855

cos 65°,220.. = 0,41912829696548804929514892701459

(√cos 65°,220.. ∙ 10) : 4 = (0,64740118.. ∙ 10) : 4 = 6,474011.. : 4 = 1,618502.. ≈ ɸ_Cheope = 1,618590..

10.

A questo punto, abbiamo già visto un bel po’ di cose che ci dimostrano che, come diceva Platone, fra il sistema della fisica e quello della matematica pura non esiste nessuna differenza. Anzi, tutto il complesso di queste argomentazioni ci spinge ad affermare che, per esempio, noi possiamo capire integralmente il significato matematico di un numero come BM (!) = 0,46163214497.. solo quando ci siamo resi conto che esso, oltre a rappresentare una grandezza astratta, costituisce anche la differenza fra il raggio classico del protone e il suo inverso. Naturalmente, potremmo anche dire l’opposto: che abbiamo compreso veramente che cosa sia il raggio classico del protone solo quanto abbiamo compreso che la differenza con il suo inverso è pari al numero più grande che possiamo ottenere da un numero positivo.

Sembra dunque giunto il momento di interrompere questa indagine particolare, e continuare il lavoro sul significato astronomico del Plateau di Giza, che è poi lo scopo precipuo di questo articolo. Ma, così facendo, abbandoneremmo l’argomento senza esserci resi conto fino in fondo delle potenzialità armoniche del prodotto fattoriale. Per averne un’idea un po’ meno approssimativa, introduciamo un’operazione un po’ particolare, ovvero il prodotto fattoriale di un altro prodotto fattoriale. Le immense potenzialità armoniche di questa operazione le possiamo scoprire immediatamente andando a controllare quale sia quel numero il cui doppio prodotto fattoriale ci dà il numero stesso moltiplicato per 10⁷⁰⁵², ovvero la x in grado di soddisfare l’equazione che vediamo qui sotto.

x !! = x ∙ 10⁷⁰⁵²

Ebbene, la soluzione di questa equazione è rappresentata un numero che oramai ci è diventato molto familiare

6,62602035900819266675..!! = 6,62602035900819266675.. ∙ 10⁷⁰⁵² = h ∙ 10⁷⁰⁵²

Come si nota immediatamente, la x in questione non è altro che il numero caratteristico della costante di Planck nel valore che attualmente viene considerato più esatto. E già questa, come si potrebbe dire, è proprio una bella coincidenza. Ma che cosa dobbiamo dire, quando scopriamo che alterando questo numero di pochi milionesimi, siamo in grado di ottenere da esso – e proprio mediante il doppio prodotto fattoriale – i numeri caratteristici di tutte le costanti della nostra scienza moltiplicati per 10⁷⁰⁵²?

6,6260200437.. !! = 6,550000.. ∙ 10⁷⁰⁵² = h_Planck ∙ 10⁷⁰⁵²

6,62599999538.. !! = 3,144729.. ∙ 10⁷⁰⁵² = (2 + Ln π) ∙ 10⁷⁰⁵²

6,62599996811.. !! = 3,141592.. ∙ 10⁷⁰⁵² = π ∙ 10⁷⁰⁵²

6,62599933822.. !! = 3,070000.. ∙ 10⁷⁰⁵² = d_p ∙ 10⁷⁰⁵²

6,625998689071.. !! = 2,99792454724.. ∙ 10⁷⁰⁵² = c ∙ 10⁷⁰⁵²

6,6259960134603.. !! = 2,718281828.. ∙ 10⁷⁰⁵² = e ∙ 10⁷⁰⁵²

6,625994986705.. !! = 2,618033.. ∙ 10⁷⁰⁵² = ɸ² ∙ 10⁷⁰⁵²

6,62599067747.. !! = 2,236067.. ∙ 10⁷⁰⁵² = √5 ∙ 10⁷⁰⁵² = (ɸ + 1/ɸ) ∙ 10⁷⁰⁵²

6,6259701400966.. !! = 1,054571628.. ∙ 10⁷⁰⁵² = ħ ∙ 10⁷⁰⁵²

6,626020548.. !! = 6,672011.. ∙ 10⁷⁰⁵² = G ∙ 10⁷⁰⁵²

11.

Per avere un’idea più chiara di quel che abbiamo scoperto, è bene notare che se facciamo il logaritmo in base 10 di 6,62602035900819266675.. ∙ 10⁷⁰⁵², quel che otteniamo è proprio 7052, più una frazione decimale

log 6,62602035900819266675.. ∙ 10⁷⁰⁵² = 7052 + 0,8212527659545333169026276774

Questa frazione decimale è pari alla tangente di un angolo il cui seno è praticamente identico a √π_Cheope – 1. La radice 81sima dell’inverso della differenza è praticamente identica a Ln π

tg x = 0,8212527659545333169026276774

x = 39°,394645550189446408544346662593

sen 39°,394645.. = 0,772792887.. ≈ √π_Cheope – 1 = 0,772810520.. (-1,763340.. ∙ 10^-5

⁸¹√1/1,763340.. ∙ 10^-5 = ⁸¹√56710,552243.. = 1,144688206.. ≈ Ln π = 1,144729885..

Inoltre, qui sotto possiamo vedere che 7052 risulta dal doppio prodotto fattoriale di una cifra che differisce dal valore esatto di π di poco più di due millesimi.

3,139189966689878140357.. !! = 7052

Quest’approssimazione di π è particolarmente interessante perché da essa possiamo ricavare un’approssimazione quasi perfetta di ɸ nel modo che segue

⁴√(3,139189966689878140357..² – 3) = ⁴√6,854513646.. = 1,618058284.. ≈ ɸ = 1,618033988..

Il 10 invece risulta dal doppio prodotto fattoriale di un numero da cui si possono ricavare delle ottime approssimazioni di dei numeri caratteristici della carica unitaria c_u = 1,6022 e della lunghezza di Planck ℓ_P = 1,616256..

2,517972041739.. !! = 10

(2 ∙ 2,517979)/π_Cheope = 1,602350.. ≈ c_u = 1,6022

Ln (2 ∙ 2,517979) = 1,616601.. ≈ ℓ_P = 1,616256..

Inoltre, se dividiamo 7052 per 10³, e interpretiamo numerologicamente il risultato come un angolo di 7°,052, scopriamo che la tangente corrisponde in modo praticamente esatto a 2/10 ∙ (ɸ_Cheope – 1)

tg 7°,052 = 0,123705917.. ≈ 2/10 ∙ (ɸ_Cheope – 1) = 0,1237180692..

12.

Date le straordinarie caratteristiche armoniche del valore della costante di Planck in connessione con il doppio prodotto fattoriale, conviene inoltre anche dare un’occhiata a quale sia la – chiamiamola così – la sua “radice fattoriale cubica”. Ovvero, in altre parole, quel numero di cui facendo per due volte il prodotto fattoriale ci da a sua volta 6,62602035900819266675. Infatti, ci prepariamo a scoprire che il suo prodotto fattoriale semplice corrisponde a un’ottima approssimazione del numero caratteristico del diametro classico del protone d_p = 3,07 mentre, se lo interpretiamo numerologicamente come un angolo, vediamo che il suo coseno corrisponde al numero caratteristico della costante di Boltzmann k = 1,38054 ∙ 10^-23 joule/K meno 1

2,4298297.. ! = 3,078321.. ≈ d_p = 3,07

2,4298297.. !! = 6,626020.. = h

tg x = 2,4298297..; x = 67°,630311765166511084542368203539

1 + cos 67°,630311.. = 1 + 0,380581.. = 1,380581.. ≈ k = 1,38054

13.

Anche manipolando un po’ il risultato di 6,62602035900819266675.. !! cominciamo presto ad avere delle sorprese. Che però oramai, dopo tutto quel che abbiamo visto, non sembreranno poi più così sorprendenti. Nei primi casi, possiamo vedere come sia possibile risalire da questo numero al numero caratteristico della costante gravitazionale

tg ₂log 6,62602035900819266675..∙ 10⁷⁰⁵² = tg 3°,848362877.. = 0,06726.. = (m_p – 1)/10 = 0,06726

–₂log ³²⁷⁶⁸√6,62602035900819266675..∙ 10⁷⁰⁵² = 0,667087.. ≈ G/10 = 0,6672

Qui sotto possiamo vedere come, trascurando la potenza di 10, quello che troviamo è il numero caratteristico del raggio classico dell’elettrone

1/²⁵⁶√6,62602035900819266675..∙ 10⁷⁰⁵² = 1/3548812209322396122420951409,6669 ≈

= 2,817844.. ∙ 10^-28 ≈ r_e = 2,81794..

Qui sotto invece vediamo che passando numerologicamente da una tangente ad un angolo e poi da questo stesso angolo a un’altra tangente, arriviamo a un’ottima approssimazione della durata di un giorno precessionale

tg x = ₃log 6,62602035900819266675..∙ 10⁷⁰⁵² = 0,58527601662245167243755015709218

x = 30°,339415068715623502560487955849

tg y = x = ³√30°,339415.. = 3,1189068281760694668713559745991

y = 72°,222842.. ≈ durata di un giorno precessionale pari a 26000 : 360 = 72,222.. anni solari

E qui sotto possiamo notare come questo numero sacro, proiettato sulla trigonometria a base 360, possa assumere dei significati ancora più ampi di quelli che abbiamo visto nel corso dei precedenti lavori

₃Ln tg 72°,222842.. = ₃Ln 3,118906.. = -2,04935.. ≈ -(√ɸ)³ = -2,058171..

tg (tg 72°,222842..) = tg 3,118906748.. = 0,054489022.. ≈ (sen + cos + tg π/2) – 1 =

= 0,054458788.. ≈ ħ – 1 = 0,054571628.. ≈ (r_p/r_e)/10 = 1,535../2,81794.. = 0,0544724160

Escludendo numerologicamente i decimali, e prendendo dunque il “mitico” angolo di 72°, vediamo che il suo coseno equivale al rapporto fra il raggio e la massa dell’elettrone

cos 72° = 0,309016.. ≈ r_e/m_e = 2,81794../9,1093.. = 0,309344296.. = cos 71°,980280794..

Il coseno dell’angolo di 72° è molto vicino a quella x in grado di soddisfare l’equazione armonica che vediamo qui sotto. E, per quanto risulti di per sé evidente, conviene sottolinearlo: queste che chiamiamo “equazioni armoniche” e le x che le soddisfano sono molto importanti per il sistema matematico che stiamo esplorando perché, trattandosi di un “sistema armonico” o di una “armonia delle sfere”, è del tutto chiaro che i numeri che stanno a suo fondamento e le loro approssimazioni siano caratterizzati dalla possibilità di instaurare rapporti simmetrici con gli altri numeri del sistema, in modo tale che si possa passare dall’uno altro senza soluzioni di continuità. Per questo nei libri sacri questo sapere è paragonato a un abito a una tunica senza cuciture.

₂inv. log x = -10 x = 3,0937458900933..

x = -0,30937458900933.. ≈ cos 72° = 0,309016..

Vedendo cose di questo genere, sembra davvero impossibile che certi numeri, il 72, il 144, il 360 etc., possano essere finiti nei libri sacri di tutto il mondo per un caso: a meno che non si cominci a chiamarlo Caso, attribuendogli al tempo stesso onniscienza e onnipotenza come a una divinità di quelle a cui una tradizione millenaria ci ha abituato (cosa che alcuni evoluzionisti, coscienti o meno che ne siano, hanno già fatto da decenni).

A noi sembra del tutto assurdo, ma nell’antichità scienza e religione erano la stessa cosa. I detentori del sapere teologico non facevano differenze fra il sapere mitopoietico e quello matematico. O, come potremmo anche dire, fra calcoli e sacramenti. Ma non perché fossero, come noi siamo inclini a credere, delle persone superstiziose. Al contrario, perché, con ogni sorta i buona ragione, essi vedevano in delle cose per noi del tutto eterogenee due diverse facce di una stessa medaglia. I Maya addirittura erano arrivati al punto di pensare a certi numeri come a delle divinità, piegate e affaticate sotto il peso del Tempo: e il Tempo era giudicato da quelle culture come l’essenza dell’Universo.

I Maya erano gente che, proprio come gli Antichi Egizi, dividevano l’anno in una parte “pura” di 360 giorni, pari ai gradi dell’angolo giro, completati da 5 giorni infausti. E, guarda caso, 360 diviso 5 fa proprio 72, un numero che può corrispondere a un giorno precessionale oppure a 4 periodi di 360 giorni ognuno composto da 18 unità di 20 giorni ciascuna. Il calendario era dunque organizzato secondo un sistema di simmetrie perfette, che rimandano al cerchio e al pentagono. Davvero gente che organizzava il calcolo del tempo secondo sistemi tanto simmetrici e complessi non sapeva nulla di tutti quei significati profondi che abbiamo scoperto dietro questi numeri e nelle figure geometriche connesse? Davvero queste persone non conoscevano la trigonometria a base 360? Sono, non diciamo fondate, ma anche solo ragionevoli un’ipotesi di questo genere?

14.

Se quello che abbiamo visto fino ad adesso non bastasse, possiamo andare a dare un’occhiata ai rapporti che, attraverso il prodotto fattoriale, si creano fra due delle costanti più fondamentali della nostra scienza empirica: la costante di Newton e quella di Planck. In prima istanza, possiamo notare che se facciamo la sottrazione fra il prodotto fattoriale di G e quello di h, possiamo da essa ricavare un’ottima approssimazione del numero caratteristico della costante che descrive il raggio del protone nel modo che vediamo qui di seguito

√log (G ! – h !) = √log (6,672 ! – 6,626 !) = √log 226,824.. = √2,355689.. = 1,534825.. ≈ r_p = 1,535

Ma questo non è che l’inizio. Se “stiriamo” il valore di queste due costanti verso l’alto, dobbiamo prepararci a una sorpresa, dato che facendo per 4 volte il logaritmo naturale della somma del loro prodotto fattoriale, otteniamo il numero di Eulero diviso per -10: il che ci ricorda che dividendo il numero caratteristico di G per quello della sua potenza, ottenevamo giusto la radice del numero di Eulero

₄Ln (6,6725..! + 6,6262..!) = ₄Ln 5018,710.. = -0,2718281828459045.. = -e/10

Qui è interessante il fatto che se facciamo la differenza fra la somma del prodotto fattoriale delle due approssimazioni di G e di h connesse con -e/10, e il prodotto fattoriale di 7, possiamo ricavare uno dei valori sperimentalmente possibili del numero caratteristico della lunghezza di Planck

1 + {{[7 ! – (6,6725..! + 6,6262..!)] ∙ 10} : 2} = 1,616273.. ≈ ℓ_p = 1,616252..

Questo fatto risulta tanto più interessante e significativo quando ci ricordiamo che il prodotto di un’approssimazione della costante di Planck “stirata” leggermente verso l’altro corrisponde esattamente a 7⁴

6,627455481..! = 2401 = 7⁴

Né il legame fra G e h si esaurisce a questo elevato di complessità, dato che da un’approssimazione di G, di nuovo un po’ stirata verso l’alto, possiamo ottenere h nel modo che vediamo qui di seguito

4 + 6,67297306.. !/10³ = 4 + 2626/10³ = 6,6261 ≈ h = 6,626

Questo risultato appare ancora più interessante quando ci rendiamo conto che la radice quadrata di 2626 corrisponde al valore di un angolo il cui coseno è praticamente identico ad h – 6

cos √2626 = cos 51°,244511901.. = 0,625998170853.. ≈ h – 6 = 0,626 (-1,829.. ∙ 10^-6

Qui scopriamo una connessione molto complessa fra il prodotto fattoriale di un valore sperimentalmente possibile di G, quello della costante di Planck e quello di un angolo il cui seno è pari a h – 6. La complessità di questa relazione si arricchisce di significato quando scopriamo che l’inverso del seno iperbolico dell’angolo di 51°,244.. non è altro che il valore di ħ² moltiplicato per 10⁴⁶

1/sinh 51°,244.. = 1,111274244.. ∙ 10^-22 ≈ ħ² ∙ 10⁴⁶ = 1,11212131.. ∙ 10^-22

15.

Scopriamo dunque che le costanti della fisica sono fra di loro connesse in un reticolo che comprende i loro prodotti fattoriali, e presi singolarmente e sommati o sottratti, e funzioni logaritmiche sia naturali sia a base 10. Ma queste relazioni, in un modo che in questo momento non appare facilmente comprensibile, si estende anche alla trigonometria. Il che spinge all’ipotesi che nel passato profondo dell’umanità sia esistito un qualcosa come una matematica che comprende in sé la geometria, o di una geometria che comprende in sé la matematica: una disciplina, per così dire, assoluta, che riesce a raccogliere in sé tutto lo scibile umano connesso con il numero.

E che questa sia un’ipotesi e non una farneticazione ce lo dimostra il fatto che, se analizziamo la struttura di 6,67297306.. ! = 2626, scopriamo che esso nasconde di nuovo quel numero del codice astronomico sacro che si è rivelato tanto importante nel corso delle nostre indagini: il 144. Infatti, 144 è proprio il risultato del prodotto dei costituenti di questo numero

2 ∙ 6 ∙ 2 ∙ 6 = 144

Se facciamo la somma delle due divisioni opposte divisioni sequenziali – che possiamo effettuare da sinistra a destra oppure da destra a sinistra – otteniamo un altro numero sacro importantissimo: il 40

1/(2 : 6 : 2 : 6) + 1/6 : 2 : 6 : 2) = 36 + 4 = 40

Se dividiamo 144 per 40, otteniamo l’angolo giro diviso per 10²

144 : 40 = 3,6 = 360/10²

Se facciamo il prodotto, scopriamo che da esso si può ricavare una discreta approssimazione di ɸ_Cheope² facendone dal radice c² = 8,98755190728516. Un’approssimazione che è quasi identica a quella che ne possiamo ricavare facendo per .. volte il logaritmo naturale

^c²√(144 ∙ 40) = ^{8,987551907..}√5760 = 2,620616210.. ≈ ɸ_Cheope² = 2,619834702..

₄Ln 5760 = -0,2620883.. ≈ ^c²√(144 ∙ 40)/-10 = 0,2620616..

Naturalmente, anche dopo aver visto tutto questo, ognuno può pensare quello che vuole. In sé, il risultato di un calcolo lo possiamo considerare oggettivo, la sua interpretazione non gode di tali privilegi. Questo premesso, a noi risulta spontaneo immaginare che tutti quei significati scientifici di cui si è mostrata portatrice la trigonometria a base 360, come anche le connessioni fra astronomia e scienza che continuiamo a scoprire nel codice astronomico sacro scoperto da de Santillana e von Dechend, fossero parte del patrimonio culturale di una casta sacerdotale come quella Antico Egizia. Un’altra ipotesi sembra impossibile: coloro che hanno fondato questo codice sapevano che attraverso di esso è possibile costruire una teoria dei campi unificati, capace di descrivere l’universo dall’infinitamente piccolo all’infinitamente grande. Ci sembra assurdo pensare che una matematica come quella che andiamo disvelando si fondi su dei numeri che sono venuti fuori cinque o più millenni fa attraverso un’interminabile concatenazione di vincite al lotto del destino. Una volta che abbiamo messo da parte i nostri pregiudizi evoluzionisti, sembra del tutto chiaro: qui abbiamo a che fare con un’antichissima forma della scienza empirica, con connotati talmente diversi dalla nostra che finora non siamo stati capaci di riconoscerla.

Capitolo 9:

RIPRESA DELL’INDAGINE SULLA STRUTTURA ARMONICA DEL SISTEMA SOLARE: LE MISURE PECULIARI DELLA TERRA COME RISULTATO DI FUNZIONI DI PI GRECO, PHI, DEL 10 E DEL NUMERO DI EULERO

1.

Chissà, forse davvero il presente rappresenta da sempre, come si dice, la punta di lancia dell’evoluzione. Forse noi siamo davvero gli esseri umani più intelligenti e scientificamente evoluti che siano mia comparsi sulla faccia della Terra, come possiamo escluderlo? Però, diciamoci la verità: a quale matematico occidentale sarebbero venuti in mente sistemi di connessioni come quelli che stiamo esplorando motu proprio, ovvero come spontanea intuizione di un nuovo universo matematico? Chi si sarebbe mai sognato di pensare all’universo dei numeri come a un reticolo intelligente, finemente strutturato, in cui degli intorni numerici particolari – come per esempio quelli che hanno un centro in h = 6,626, oppure in π, oppure in ɸ, etc. – hanno lo steso ruolo di quei neuroni del cervello umano che, pur esteriormente identici agli altri, si caratterizzano per un numero enorme di connessioni?

Al contrario, buona parte dei matematici hanno alzata da un bel po’ di anni bandiera bianca, e il mondo dei numeri si è cominciato a immaginarlo come un guazzabuglio di tecniche, che hanno in comune soltanto il principio di non contraddizione.

Quanto alla fisica, non è che le cose andassero in modo molto diverso. Da più parti si era arrivati alla conclusione che scoprire una logica comune fra la meccanica quantistica e quella relativista fosse un compito del tutto impossibile. Alla fisica veniva affidato il compito prettamente tecnico di estendere la potenza dei mezzi a disposizione degli esseri umani. Nessuno si aspettava che potesse di colpo risorgere in essa una finalità ontologico-teologica davvero profonda. In effetti, quale fisico avrebbe mai osato ipotizzare che fisica e matematica pura sono la stessa cosa, che cogliere i moti degli astri è come cogliere i moti del pensare divino? Chi avrebbe mai sospettato che le costanti fisiche sono dei numeri puri attraverso cui Dio ha formato l’universo per mezzo di una “materia” che altro non è che una sorta di etere matematico, indefinibile e inafferrabile, che rimane identico in ogni suo mutare?

Dobbiamo riconoscerlo umilmente. Con ogni probabilità, a nessun intelletto occidentale, per quanto vasto e possente, sarebbero mai venute in mente queste idee. Se non le avessimo potute decriptare a partire dalle misure della Grande Piramide, ci sarebbero rimaste per sempre ignote. I numeri ci sarebbero sembrati per chissà ancora quanto tempo il frutto di un caos di tecniche più o meno senza nesso, il cosmo un caos di fuochi fatui saltati fuori chissà come da un’esplosione avvenuta in tempi immemorabili. Chi si sarebbe mai sognato di ipotizzare che tutte le grandezza atomiche o astronomiche di un qualche rilievo che possiamo misurare si possano derivare da quei numeri fondamentali che furono criptati nella Grande Piramide? Men che meno avremmo pensato che si potrebbe far lo stesso a partire dal codice astronomico sacro che fu trasposto nel mito, e di cui per primi hanno compreso l’importanza scientifica Giorgio de Santillana e Hertha von Dechend.

Scoperte come queste dovrebbero convincerci ad assumere una ben diversa prospettiva di fronte a concetti – che giudichiamo arcaici – come quelli di un cosmo teleologicamente ordinato in ogni sua parte. Forse noi quest’ordine finora non siamo stati capaci di scoprirlo non perché non esista, ma perché è talmente onnicomprensivo e perfetto che, ad occhi dotati di vista non abbastanza acuta, può sembrare indistinguibile dal caos. Proprio come il cervello umano: è strutturato in modo talmente fine che, a prima vista, non sembra possedere alcuna struttura. Oppure, che la sua struttura sia talmente e brutalmente semplice, che sembra impossibile che possa essere il riflesso di una possente mete creatrice.

2.

A favore dell’ipotesi di un cosmo ordinato abbiamo già trovato un bel po’ argomenti. A parte tutto quel che abbiamo visto negli articoli precedenti, in questo lavoro abbiamo già mostrato come i numeri connessi con la durata dei cicli dei pianeti hanno dei rapporti più o meno evidenti con il codice astronomico sacro individuato da de Santillana e von Dechend. Adesso ci apprestiamo ad andare ancora più a fondo, e a dimostrare che la massa della Terra, è uno dei valori che il Creatore ha derivato dall’intorno numerico che ha il suo centro in π. E se teniamo conto di tutti quelle meravigliose relazioni armoniche π, per mezzo del prodotto fattoriale, intrattiene con una gran quantità di dati scientifici e di grandezze matematiche di rilievo, vengono davvero le vertigini: la medesima intelligenza, le medesime proporzioni, percorrono l’universo in ogni sua parte, in ogni suo dettaglio. Non si trova in esso una maggior quantità di caso o di caos che in uno spartito di Mozart o di Beethoven.

Possiamo constatare la verità di quest’affermazione a partire dall’equazione che vediamo qui sotto. Se prendiamo il valore della massa della Terra espresso in chili (5,966 ∙ 10²⁴ kg) e facciamo per tre volte il logaritmo in base 10, noi vediamo che esso corrisponde a un valore pari a circa Ln π – 1

₃log 5,966 ∙ 10²⁴ = 0,144270.. ≈ Ln π – 1 = 0,144729..

Ma la conferma più spettacolare della derivazione della massa della Terra da π ci viene dal fatto che, se prendiamo l’approssimazione che abbiamo scelto qui sotto e facciamo la differenza fra il triplo logaritmo naturale e il doppio logaritmo in base 10, ecco che ci rendiamo conto che il risultato non è altro 1/π diviso per 10²

₃Ln 5965314025539638299905696,639846 – ₂log 5965314025539638299905696,639846 =

= 1,3972078635257959852814001817666 – 1,3940247646639580785660225064991 =

= 0,00318309886183790671537767526744 = 1/(π ∙ 10²)

Un fatto notevolissimo sembra che, se facciamo la media fra i due numeri, quello che otteniamo è un’approssimazione della radice cubica del numero di Eulero che differisce dal numero esatto di poco più di 38 milionesimi

(1,397207863.. + 1,394024764..) : 2 = 1,395616314.. ≈ ³√e = 1,395612425.. (3,889.. ∙ 10^-6

Inoltre, se facciamo il prodotto fattoriale del doppio logaritmo in base 10 della massa della Terra (1,394024..), quello che otteniamo è, incredibilmente, 2 ∙ (ɸ_Cheope – 1). E, ancor più incredibilmente, questo è il medesimo risultato che possiamo ricavare dal rapporto fra il raggio della prima orbita dell’elettrone pari a 1bohr = 5,3 ∙ 10^-11 con il raggio classico del protone

₂log 5965314025539638299905696,639846 = 1,3940247646639580785660225064991

1,394024764663..! = 1,23734417.. ≈ 2 ∙ (ɸ_Cheope – 1) = 1,237180692..

⁸¹√(1bohr/r_p) = ⁸¹√(5,3 ∙ 10^-11 : 1,535 ∙ 10^-18) = ⁸¹√34527687,296… = 1,23897.. ≈ 2(ɸ_Cheope – 1) = 1,23718..

Dunque, la massa della Terra risulta una complicata funzione di π, ɸ, del 10 e del numero di Eulero: proprio come il lato della Grande Piramide.

3.

È stato segnalato più volte in passato come le misure di questo straordinario monumento contenessero in codice un gran numero di dati astronomici. Coloro che sono stati capaci di decodificare tali informazioni sono stati oggetto di dileggio da parte di tutta o quasi tutta la scienza ufficiale. L’obiezione che è stata sistematicamente fatta è che, manipolando i numeri, si può far sì che qualsiasi contenga qualsiasi cosa. Ma, ovviamente, anche una legge come quella di Newton è un “manipolare numeri”. Quello che distingue un calcolare a vuoto da una legge scientifica che giunga al cuore matematico della realtà è il fatto che il calcolare a vuoto non è in grado di fare previsioni. Si può ben calcolare la distanza dalla Luna a partire dal numero di margherite che si trovano nel proprio giardino. Da una cosa come questa non possiamo trarre previsioni quanto a tutto il resto della realtà.

Ma qui le coste stanno in modo molto diverso. Noi abbiamo previsto e inesorabilmente verificato delle connessioni sistematiche fra punti di unicità della trigonometria e leggi scientifiche. Abbiamo previsto e sistematicamente verificato connessioni fra equazioni armoniche e cicli cosmici. Abbiamo previsto e sistematicamente verificato che il codice dell’astronomia sacra, individuato da de Santillana e von Dechend corrispondesse a caratteristiche nascoste dei cicli e degli oggetti astronomici.

Certo, stante le nostre abitudini e attitudini culturali, è facile che, a dispetto di ogni evidenza, si possa credere che certi rapporti che sono alla base della massa della Terra siano un caso. Ma se adesso andiamo a vedere anche gli altri parametri fondamentali, il raggio polare, il raggio equatoriale e le distanze minima, massima e media della Terra dal Sole, ecco che ci rendiamo conto quelle proporzioni armoniche che abbiamo individuato riguardo alla massa rispuntano fuori. E, per di più, hanno dei tratti di raffinatezza ancor più impressionanti. Le analisi che ci apprestiamo a esporre non lasciano dubbi: nessuna delle misure fondamentali del nostro pianeta è frutto del caso.

Possiamo partire da un rapporto che, in apparenza, non ha nulla a che vedere con questo argomento, ovvero quello che vediamo qui sotto, fra i due forse valori più comunemente accettati della costante gravitazionale e della costante di Planck

6,67/6,626 = 1,0066405..

Ebbene, questo valore, che come al solito non sembra aver nulla di speciale corrisponde in modo quasi esatto al rapporto fra il raggio equatoriale e polare della Terra, elevato al quadrato

(6378 : 6357)² = 1,00330344..² = 1,006617.. ≈ G/h = 6,67/6,626 = 1,0066405.. (-0,000023)

Questo stesso rapporto, elevato alla 16sima potenza, ci da anche un’ottima approssimazione della costante di Dirac,

(6378 : 6357)¹⁶ = 1,00330344..¹⁶ = 1,054185.. ≈ ħ = 1,054571.. ≈ G/h⁸ = (6,67/6,626)⁸ =

= 1,0066405..⁸ = 1,054375.. ≈ ħ = 1,054571..

Naturalmente, dopo quello che abbiamo visto sopra, ci aspettiamo che i rapporti armonici che possiamo trovare attraverso il raggio polare e quello equatoriale siano più raffinati, e dunque più articolati e complessi di un semplice rimando a due costanti fisiche fondamentali. E infatti le cose stanno proprio così.

Facendo il prodotto e poi per 3 volte il logaritmo in base 10, troviamo un numero che oramai ci sarà diventato familiare. Esso corrisponde non solo alla costante di Dirac meno 1, ma anche alla tangente di un angolo molto prossimo a π.

– ₃log (6378 ∙ 6357) = –₃log 40544946 = 0,05489254542.. ≈ ħ – 1 = 0,054571628..

tg x = 0,05489254542.. ; x = 3,141957.. ≈ π = 3,141592..

Se invece ne facciamo la radice 64sima, quello che otteniamo è un valore prossimo a 1 + π/10. L’inverso della differenza con il valore esatto corrisponde in modo quasi perfetto alla durata del ciclo di Sirio (1461 anni solari). La differenza con il ciclo di Sirio corrisponde con il logaritmo in base 10 della costante gravitazionale. La sua radice quarta è un’ottima approssimazione di 10 ∙ (ɸ_Cheope – 1)

⁶⁴√40544946 = 1,314843.. ≈ 1 + π/10 = 1,3141592.. (+6,840759.. ∙ 10^-4

1/(+6,840759.. ∙ 10^-4 = 1461,825906.. ≈ 1461 (+0,825906.. ≈ log G = log 6,7 = 0,826074

⁴√1461,825906.. = 6,18335119.. ≈ 10 ∙ (ɸ_Cheope – 1) = 6,18590346..

A questo punto nessuno si stupisce di scoprire che, proiettato sulla trigonometria a base 360° l’angolo di 40544946° corrisponde a un angolo d’importanza simbolica e scientifica quale quello -54°: dunque, esso è intimamente connesso con il numero d’oro, e con tutte le nozioni scientifiche che dal numero d’oro abbiamo potuto ricavare. Il legame con la geometria sacra viene rafforzato dal fatto che se facciamo la somma dei componenti di 6378 (6 + 3 + 7 + 8 = 24) e la dividiamo per la somma di quelli di 6357 (6 + 3 + 5 + 7 = 21) il risultato è pari a π_Cheope – 2

24 : 21 = 1,142857.. = π_Cheope – 2

4.

Già a questo punto, difficilmente si continuerebbe a pensare che le misure caratteristiche della Terra siano frutto del caso. E che dire poi, quando ci rendiamo conto che il raggio equatoriale può essere derivato direttamente da una funzione trigonometrica assolutamente astratta, ovvero da quell’angolo il cui valore risulta identico al coseno, così che x = cos x.?

Questo angolo risulta dal limite della funzione cos x applicata in modo sequenziale ai suoi stessi risultati.

Il lettore può fare la prova sulla sua stessa calcolatrice. Se prende un numero qualsiasi e applica la funzione ripetutamente, scopre che il valore che appare sul quadrante si aggiusta rapidamente verso un limite che è quello che possiamo vedere qui sotto (la “n” in “_ncos x” rappresenta il numero di ripetizioni sequenziali della funzione al suo stesso risultato, che in questo caso tende all’infinito)

Lim_{n→∞ n}cos x = 0,9998477415310881129598107686798

Questo valore del coseno corrisponde a quello del seno dell’angolo complementare

sen y = Lim_{n→∞ n}cos x = 0,9998477415310881129598107686798

y = 89°,000152258468911887040189231321

Questo angolo ha, come ci apprestiamo a scoprire, varie caratteristiche molto interessanti. La sua radice quarta è pari a un’ottima approssimazione del diametro classico del protone, la sua radice nona è vicina alla radice quadrata del numero di Eulero.

⁴√89°,000152.. = 3,071479.. ≈ d_p = 3,07

(⁹√89°,000152..)² = 1,646641..² = 2,711427.. ≈ e = 2,718281.. (-0,00685465375874462540220018225194

In questo secondo caso, possiamo notare come la radice sedicesima dell’inverso della differenza è pari a 1 più un’ottima approssimazione dell’anno solare (365,25 giorni) divisa per 10³

¹⁶√1/0,006854653.. = ¹⁶√145,886.. = 1,365371.. ≈ 1 + 365,25/10³ = 1,36525

Oppure, se moltiplicata ancora una volta per 10³, questa differenza corrisponde con ottima approssimazione a ɸ⁴. In questo secondo caso l’inverso della differenza corrisponde ancora una volta il numero caratteristico della costante che descrive il diametro classico del protone moltiplicato per 10⁴

⁴√(0,006854653.. ∙ 10³) = ⁴√6,854653.. = 1,618066552.. (+3,256415.. ∙ 10^-5

1/3,256415.. ∙ 10^-5 = 3,070861.. ∙ 10⁴ ≈ d_p ∙ 10⁴ = 3,07 ∙ 10⁴

Già a questo punto abbiamo trovato delle relazioni di straordinario interesse. Ma ancora non siamo giunti al punto veramente importante della nostra analisi. Infatti, se il valore assoluto dell’angolo connesso con il limite della funzione cos x appare intimamente connesso con il numero d’oro e con il diametro classico del protone, adesso ci apprestiamo a scoprire che tanto il coseno che la tangente di quest’angolo sono altrettanto intimamente connessi con π.

Cominciamo con il coseno. Se ne facciamo l’inverso, scopriamo che si tratta di un valore molto vicino a 360/2π.

x = 89°,000152258468911887040189231321

1/cos 89°,000152.. = 1/0,017449749.. = 57,307413151.. ≈ 360/2π = 57,295779513.. (+0,01163363865226..

La differenza con il valore esatto, se elevata al cubo ci dà un valore prossimo a π/2 ∙ 10^-6. Se invece ne facciamo la radice ottava ci dà un valore prossimo a π/2 – 1. Nel primo caso, possiamo notare che la differenza si connette con il numero di Eulero

0,01163363..³ = 1,574514.. ∙ 10^-6 ≈ π/2 ∙ 10^-6 = 1,570797..(+3,71834.. ∙ 10^-9 ≈ (e + 1) ∙ 10^-9 = 3,71828.. ∙ 10^-9

⁸√0,01163363865226.. = 0,573078.. ≈ π/2 – 1 = 0,570797..

Se adesso passiamo alla tangente, scopriamo che si connette a 360/2π in un modo ancora più esatto

tg 89°,000152.. = 57,298687.. ≈ 360/2π = 57,295779 (+0,00290809966848336243857445367042

In questo caso, abbiamo scritto la differenza per esteso perché la radice del suo inverso non è altro che la radice cubica del raggio equatoriale della Terra. Un fatto altamente simbolico questo, dato che il raggio equatoriale è leggermente maggiore di quello polare: proprio come il perimetro del cerchio che verrebbe fuori se lo tracciassimo per mezzo di questa approssimazione di 2π.

(√1/0,00290..)³ = (√343,867168..)³ = 18,543655..³ = 6376,554407.. ≈ 6378

Inoltre, 18,543655.. costituisce un valore molto interessante perché non è altro che un’ottima approssimazione di 30/ɸ. Ma questo lo vedremo nella fase successiva dell’analisi, in connessione con l’analisi del raggio polare.

5.

A questo punto, possiamo provare ad applicare al raggio equatoriale e polare della terra altri strumenti di analisi oltre a quelli consueti. Stiamo parlando di quella che potremmo definire come analisi strutturale dei numeri, che abbiamo sopra applicato in modo particolarmente profondo alle misure della Piramide e alla durata dell’anno solare e di quello lunare.

Possiamo cominciare facendo il rapporto fra la divisione delle migliaia, per le centinaia, per le decine, per le unità. In questo modo troviamo uno dei rapporti che, come abbiamo visto in The Snefru Code parte 3, caratterizzavano le misure dell’Arca, quello fra il quinto e il sesto numero della serie di Fibonacci.

(6000 : 300 : 70 : 8) : (6000 : 300 : 50 : 7) = 1/28 : 2/35 = 5 : 8 = 0,625

Lo stesso accade facendo il rapporto fra i prodotti dei costituenti del numero. Dunque adesso noi possiamo essere praticamente certi che le misure dell’Arca non erano altro che la riproduzione dei rapporti armonici che legano il raggio polare ed equatoriale della Terra

(6 ∙ 3 ∙ 5 ∙ 7) : (6 ∙ 3 ∙ 7 ∙ 8) = 630 : 1008 = 630 : 1008 = 0,625

E qui possiamo notare che tanto il 630 che il 1008, come somma dei componenti, danno 9, e che componendo numerologicamente il prodotto del numero della migliaia per le centinaia, e di quello delle decine per le unità del valore del raggio equatoriale della Terra possiamo costruire numerologicamente un valore molto vicino a quello della sua radice cubica

6 ∙ 3 = 18; 7 ∙ 8 = 54;

18,54 ≈ ³√6378 = 18,545..

Se poi facciamo il prodotto delle migliaia per le centinaia, per le decine per le unità del raggio equatoriale, noi vediamo che i doppio logaritmo in base 10 corrisponde con ottima approssimazione all’inverso di π/c e dunque all’inverso del lato Est-Ovest della Camera del Re diviso per 10. Dunque, adesso sappiamo che fra i dati astronomici codificati in questa che è la struttura interna di maggior rilievo della Piramide c’è anche il raggio equatoriale della Terra

1/₂log(6000 ∙ 300 ∙ 70 ∙ 8) = 1/₂log 1008000000 = 1/0,954409.. = 1,047768.. ≈ π/c = 1,047922.-

Inoltre, se prendiamo i due numeri isolati, scopriamo come prima cosa che entrambi risultano delle funzioni approssimate di ɸ_Cheope

³√-₃log 6378 = ³√0,236333.. = 0,618265.. ≈ (ɸ_Cheope – 1) = 0,618590..

³√-₃log 6357 = ³√0,23645…. = 0,618372.. ≈ (ɸ_Cheope – 1) = 0,618590..

Se invece facciamo la radice cubica, in entrambi i casi troviamo che si tratta ancora di funzioni di ɸ_Cheope

³√6378 : 3 = 18,545056.. : 3 = 6,181685.. ≈ 10 ∙ (ɸ_Cheope – 1) = 6,18590346..

³√6357 : 3 = 18,524680.. : 3 = 6,17489.. ≈ 10/ɸ_Cheope = 6,178215..

La seconda di queste funzioni, è molto interessante. In primo luogo, perché il suo valore corrisponde a quello della tangente di un angolo il cui seno iperbolico è uguale alla sua tangente moltiplicata per 10³⁴, ovvero alla tangente dell’angolo x in grado di soddisfare l’equazione che vediamo qui sotto

sinh x = tg x ∙ 10³⁴ x = 80°,801593729696805835032970788939

sinh 80°,801593.. = 6,1752748234118.. ∙ 10³⁴; tg 80°,801593.. = 6,1752748234118..

E qui conviene segnalare che il seno di quest’angolo è pressoché pari a π²/10 e che la radice quarta del suo valore corrisponde ad una discreta approssimazione di c = 2,9979246

√(10 ∙ sen 80°,801593..) = √9,871407119.. = 3,141879.. ≈ π = 3,141592..

⁴√80°,801593.. = 2,9981612.. ≈ c = 2,9979246

Inoltre, come si può notare, essa è vicinissima al risultato che si può derivare dal rapporto fra il raggio classico del protone r_p = 1,535 ∙ 10^-18 m, e il raggio della prima orbita dell’elettrone 1bohr = 5,3 ∙ 10^-11 m.

{[₂Ln (1bohr/r_p) – 1] : 3} ∙ 10 = [₂Ln (5,3 ∙10^-11 : 1,535 ∙10^-18) – 1] : 3} ∙ 10 =

= {[₂Ln 34527687,296 – 1] : 3} ∙ 10 = [(2,854011.. – 1) : 3] ∙ 10 =

= (1,854011 : 3) ∙ 10 = 0,618003.. ∙ 10 = 6,18003.. ≈ 10/ɸ_Cheope = 6,178215..

Sembra molto notevole il fatto che se avessimo adottato raggio della prima orbita pari a 1bohr = 5,32031, che rientra nei margini consentiti dal principio di indeterminazione, il rapporto con il raggio del protone sarebbe venuto identico alla durata dell’anno delle eclissi (346,6) moltiplicato per 10⁵. In questo modo, vediamo in trasparenza quanto siano stretti i rapporti fra l’infinitamente grande e l’infinitamente piccolo, quanto l’uno si rispecchi nell’altro. E il rispecchiamento lo si vede anche nel fatto che, proprio come accade nel caso dell’atomo, anche nel caso del sistema solare, trovandoci in un sistema armonico, siamo in grado di dedurre ogni parametro dall’altro. Infatti, possiamo ricavare la distanza massima del Sole dalla Terra a partire dall’approssimazione del 10 ∙ (ɸ_Cheope – 1) che abbiamo ricavato dal raggio equatoriale della Terra. Questo significa che il raggio dell’orbita della Terra intorno al Sole ha una relazione armonica con il suo stesso raggio: ma questo è quello che, a partire da The Snefru Code parte 3, abbiamo visto accadere anche in rapporto alle orbite dell’elettrone intorno al nucleo. Dunque quell’armonia divina che regna nell’infinitamente piccolo, dove i componenti sono solo 3 (protone, neutrone, elettrone) e tutti inesorabilmente eguali, e dove il raggio delle orbite è inesorabilmente fissato da una costante, regna anche a livello macroscopico, dove i componenti sono potenzialmente infiniti e infinite le orbite possibili

10^{(2 + 6,181685..)} = 10^8,181685.. = 151944734,351.. ≈ 152100000 km, max distanza della Terra dal Sole

Questo significa che la radice 81sima della distanza massima fra il Sole e la Terra (152100000 km) corrisponde in modo praticamente perfetto a 1 + (1 + ɸ_Cheope)/10

⁸¹√152100000 = 1,2618680.. ≈ 1 + (1 + ɸ_Cheope)/10 = 1,2618590..

Dal doppio logaritmo in base 10 della distanza massima della Terra dal possiamo dedurre anche l’inclinazione della Terra sul piano dell’eclittica. Infatti come abbiamo visto in The Snefru Code parte 4, la Terra oscilla fra i due solstizi – e dunque anche fra i due poli di un semiciclo precessionale – di un angolo che va da un minimo di 43° a un massimo di 47°secondo lo schema che vediamo qui sotto

Quindi il minimo dell’oscillazione, sommato ai 180° della metà dell’angolo giro ci danno un valore prossimo alla sezione aurea di 360°, dato che 180° + 43° = 223° e 360°/ɸ = 222°,490. Ma il doppio logaritmo della distanza massima della Terra dal Sole ci un valore molto prossimo alla tangente di 222°,49..

tg x = log (log (152100000 = 0,912866333..

x = 222°,3919.. ≈ 360°/ɸ = 222°,490..

Il seno di questo angolo è a sua volta piuttosto significativo, in quanto corrisponde con buona approssimazione alla costante gravitazionale G – 6

-sen 222°,3919.. = 0,674198.. ≈ G – 6 = 0,672

E qui possiamo trovare un punto di connessione importantissimo fra la struttura del sistema solare e quella dell’atomo. Infatti, se facciamo la radice del rapporto fra il raggio classico del protone 2,8179403267 ∙ 10^{– 15} m, e il raggio della prima orbita 1bohr = 5,3 ∙ 10^-11 m, il risultato corrisponde a una buona approssimazione di 360°/ɸ². La differenza corrisponde in modo pressoché perfetto alla durata dell’anno solare diviso per 10³

√1bohr/r_p = √(5,3 ∙ 10^-11 : 2,8179403267 ∙ 10^{– 15}) = √18808,0632857355.. =

= 137,142492.. ≈ 360°/ɸ² = 137°,507764.. (-0,365271.. ≈ 365,25/-10³ = -0,36525..

Dunque, adesso non ci stupiremo se a partire dall’approssimazione di 10/ɸ_Cheope che abbiamo ricavato dal raggio polare della Terra, possiamo ricavare la distanza minima della Terra dal Sole

[2/(6,1748936538../10)]¹⁶ = 3,23892217..¹⁶ = 146692601,926.. ≈ 147100000 km, minima distanza della Terra dal Sole

Neppure ci stupiremo più di tanto quando scopriamo di poter ricavare la distanza media della Terra dal Sole (circa 149597000 chilometri) a partire entrambe le approssimazioni di ɸ_Cheope che abbiamo or ora ricavato

{1 + [1/(6,181685.. : 10)]²/10}⁸¹ = [1 + (1,617681739..²/10)]⁸¹ =

= 1,2616894209205..⁸¹ = 150365910,351.. ≈ 149.600.000

[1 + ( 1 + 6,17489../10)²]⁸¹ = [1 + (1,617489..²/10)]⁸¹ =

= 1,2616271847..⁸¹ = 149766300,953.. ≈ 149.600.000

Infine, anche nel caso della massima velocità angolare del Sole (0°61’12”,4, = 1°020111..) e della minima (0°57’13”,6 = 0,953777..) siamo in presenza di una relazione armonica, perché queste cifre si fondano su uno dei numeri che furono codificati nella Grande Piramide. Infatti, la somma delle velocità massima e minima elevata alla quarta ci da un numero molto simile a e^e

(1°020111.. + 0°,953777..)⁴ = 1,9738888..⁴ = 15,180662.. ≈ e^e = 15,154262.. (+0,02640047..

Se di questa differenza facciamo la radice c² = 8,98755190728516, a sua volta pari ai gradi della minima declinazione di Orione sul Meridiano di Giza, quel che troviamo è la costante gravitazionale divisa per 10

^{8,98755190728516}√0,02640047.. = 0,667403.. ≈ G/10 = 0,6672

Le misure caratteristiche della Terra, i suoi raggi caratteristici, il raggio della sua orbita e la sua massa, per così dire, fanno il verso a quelle dell’atomo, nel senso che la loro struttura armonica ha gli stessi fondamenti. Da questo punto di vista, abbiamo l’ennesima dimostrazione della verità delle antiche credenze che vedono nel microcosmo uno specchio del macrocosmo, e vice versa. Quindi, possiamo passare dall’uno all’altro con relativa facilità, anche dobbiamo confessare che non è chiaro il perché, per esempio, la massa della Terra sia stata scelta attraverso quel particolare intreccio fra funzioni di π e del numero di Eulero, e non altre. Abbiamo però conseguito la prova che anche alla base di misure che potevano sembrare del tutto casuali, ci sono quegli stessi numeri che alla base delle misure della Grande Piramide e – come abbiamo abbondantemente dimostrato nei precedenti lavori – di tutta l’arte e l’architettura sacra Antico Egizie.

Capitolo 10:

ALCUNE CONCUSIONI PROVVISORIE

1.

Chi sia giunto alla lettura di queste righe che concludono la prima parte del nostro lavoro, fra le altre riflessioni a cui può essere stimolato, può anche pensare di aver scoperto o di star scoprendo qualcosa di nuovo: una forma del sapere inusitata, o addirittura quasi inimmaginabile, a partire dai presupposti della nostra scienza empirica. Nemmeno nel più folle dei sogni uno scienziato occidentale “serio” sarebbe arrivato a credere che l’ordine matematico dell’universo potesse arrivare fino al punto che dal raggio equatoriale della Terra si potesse calcolare la sua distanza massima dal Sole, e che a partire dalla sua distanza massima dal Sole si potesse calcolare la tangente dell’angolo della sua inclinazione rispetto all’eclittica.

In questo senso, le pagine che abbiamo letto sono senz’altro una novità: ma solo se ci riferiamo alla cultura Occidentale moderna. Con qualche sfumatura di dubbio possiamo pensare che un tal modo di concepire l’universo sia qualcosa di nuovo anche per l’Occidente in generale, anche se le proporzioni con cui furono concepite le cattedrali, o gli angoli dell’Allineamento di San Michele lasciano aperto il dubbio che anche in quei secoli, che la cultura scolastica ci spinge a ritenere bui, non ci fosse più luce di quanta non ne abbia portata l’Illuminismo (che invece ha portato più oscurità di quanto il suo nome non vorrebbe augurare).

Ma, in assoluto, quello che abbiamo visto in queste pagine non è affatto una “scoperta”, bensì la riscoperta di un sapere che affonda le sue radici in abissi di tempo imperscrutabili. E sembra anche praticamente certo che l’origine di un tale sapere non possa essere l’intelletto umano che, come abbiamo già accennato in alcuni lavori passati, un tale sapere può intenderlo, ma non può né costruirlo né, con ogni probabilità, dedurlo empiricamente dalla realtà.

Infatti, le comprensione del sistema armonico sulla base del quale la Mente Divina ha generato l’universo si fonda sul possesso del sistema metrico decimale, che sembra il solo il grado di permettere il suo rispecchiarsi nell’intelletto umano. Per esempio, in una costante come quella di Planck, compaiono i chili e i secondi. Storicamente il chilo è nato come la massa di un decilitro d’acqua a 4°: dunque il chilo presuppone il metro e i gradi centigradi e la scelta dell’acqua come sostanza campione. Diamo per “ragionevole” la scelta dell’acqua come sostanza campione, data la sua enorme diffusione sul nostro pianeta (ma con uno scolio: se era così ragionevole, perché non l’hanno fatto tutte le culture, o, comunque sia, molte culture, e molto tempo prima?). Al contrario però, la scelta del metro presuppone che a qualcuno, chissà perché, sia venuto in mente di stabilire un’unità di misura pari a 1/10000000 del meridiano terrestre fra il polo e l’equatore e che a qualcun altro – un’intera società – gli sia venuto in mente di dargli retta. E non c’è al mondo persona capace di comprendere le ragioni di questa scelta Infatti, vista così, questa frazione pari a 1/10⁷ non ha proprio nessun significato.

2.

Invece, ovviamente, le cose non stanno affatto così. Al di là del tratto di spazio che si è scelto di suddividere in questo modo, già il modo in cui lo si è frazionato allude a tutto il sistema armonico che per mezzo di esso si è poi scoperto in queste pagine. Infatti, facendo la radice sedicesima di 1/10⁷, o andando a vedere a quale seno iperbolico corrisponde il suo inverso, ecco che ci rendiamo conto che questa frazione fa riferimento alla durata dell’anno solare (365,25 giorni), diviso per 10³, come anche al 2 e alla radice di 2

¹⁶√1/10⁷ = 0,365174.. ≈ 365,25/10³

(-¹⁶√1/10⁷!)² = (-0,365174..!)² = 1,414417..² = 2,000577.. ≈ 2

₂inv. Ln ¹⁶√1/10⁷ = ₂inv. Ln -0,365174.. = 2,001858.. ≈ 2

sinh x = 10⁷; x = 16°,811242..

y = 360° : 16°,811242.. = 21°,414240672.. ≈ (2 ∙ 10) + √2 = 21,414213562..

sen 21°,414240672.. = 0,365108.. ≈ 365,25/10³

Per altro verso bisogna fare la radice nona di 1/10⁷, o andare a vedere a quale angolo corrisponda una tangente pari al seno di 21°,414240672.., per comprendere le sue connessioni con la velocità della luce

(1/⁹√1/10⁷) : 2 = 2,99742125.. ≈ c = 2,9979246

tg x = sen 21°,414240672.. = 0,365108..

x = 20°,057551.. ≈ e^2,9979246 = 20,043894.. (+0,01365709590589952249442030005002

Ma, come abbiamo visto più volte in queste pagine, nulla in questo sistema è lasciato al caso: nemmeno le piccole differenze che noi crediamo trascurabili o casuali. Per esempio, la differenza che vediamo sopra, senza che sul momento ce ne possiamo rendere conto, è una funzione praticamente perfetta di ɸ_Cheope, e la differenza dalla perfezione è una funzione del numero caratteristico della costante di Planck h = 6,626

x = 1/0,013657095.. = 73°,222009048645921167681529845902

sen⁶⁴ 73°,222.. = 0,957430452..⁶⁴ = 0,061782170.. ≈ 1/10ɸ_Cheope = 0,061782155.. (-1,5079.. ∙ 10^-8 ≈

≈ 1/h ∙ 10⁷ = 1,5092.. 10^-8

In particolare, quella differenza di 1,5079.. ∙ 10^-8 si lega a un numero particolarmente sacro ai Maya, vale a dire il 26 che dunque, per questa via, si collega a sua volta alla costante di Planck

₂log 26 = 1,50748259.. ≈ 1,5079..

Per altro verso, a conferma della fittissima trama rete di interrelazioni che in questo sistema lega ogni parte con l’altra, possiamo notare come l’angolo di 73°,222009.. – oltre a potersi ricavare con buona approssimazione aggiungendo 1 alla durata di un giorno precessionale pari a 26000 : 360 = 72,222.. – è anche una funzione della sezione aurea dell’angolo giro. La differenza con il numero esatto è un’approssimazione di una funzione di π, che a sua volta differisce da quella esatta di una funzione della costante di Dirac ħ = 1,054571628..

sin² 73°,222009.. = 0,957430452..² = 0,916673071.. ≈ tg 360°/ɸ = 0,916081915.. (+5,911564268396.. ∙ 10^-4 ≈

≈ (π/5)¹⁶ = 5,9003516251624.. ∙ 10^-4 (-0,00000112126432336.. ≈ -(ħ²) ∙ 10^-6 = 0,00000111212131858..

E qui dobbiamo domandarci: come è possibile che una scimmia, andando avanti per tentativi ed errori, possa arrivare – dopo un paio di milioni di anni evoluzione e di “trials and errors” – a scegliere in base a criteri per di più quasi incredibilmente astratti e cervellotici un’unità di misura dello spazio tanto preziosa come il metro, senza del quale tutto il sistema armonico che stiamo disvelando sarebbe destinato a rimanere nascosto? Qui abbiamo appena dimostrato che già l’operazione sorgiva con cui si è suddiviso quell’arco di cerchio tanto lontano dal senso comune risulta enormemente significativa in relazione, per esempio, a una trigonometria come quella a base 360, che noi supponiamo nata in un contesto di arretratezza e di barbarie, e che poi invece si mostra capace di contenere in codice nulla di meno che una teoria dei campi unificati: chi può credere che questo sia l’esito accidentale di una serie mostruosa di milioni e milioni di estrazioni del lotto, in cui il caso ogni volta avrebbe scelto fra un numero smisurato di opzioni, in linea di principio da considerarsi tutte uguali e tutte sullo stesso piano?

Come lasciamo perdere i nostri pregiudizi e guardiamo in faccia la realtà, siamo costretti a riconoscere che già a questo punto la navicella del “caso evolutivo” si muove in un oceano di possibilità talmente grande da sfiorare l’impossibilità. Ma la scelta del metro, come tutti sappiamo, non è che il punto iniziale di un sistema enormemente più complesso. Infatti il metro è solo una parte, per quanto importante, del sistema metrico decimale

Dobbiamo poi aggiungere che il secondo discende dalla frazione del giorno in 24 parti: ma perché non in 20, o in 18, o in 36? E perché poi dividere ognuna di queste 24 parti in frazioni di 60 e queste frazioni in altre 60 parti? Perché non in 50 o in 100? Oppure in altre 24? In fondo, la temperatura si divide proprio in cento parti, un multiplo di 10: perché accogliere nel sistema decimale i vetusti sessantesimi per misurare il tempo?

3.

Bisogna avere la mente resa cieca e sorda dal pregiudizio per non vedere come stanno le cose. Qui non possiamo affatto parlare di caso, qualunque cosa sia. Il sapere scientifico che stiamo manipolando è intriso di una saggezza antica, di cui finora non avevamo coscienza. Probabilmente, di una saggezza eterna, dato che esso sembra quello con cui Dio ha elaborato le proporzioni dell’universo. Ma se, come sosteneva Platone, il tempo è una copia mobile dell’eternità, proprio come l’eternità il tempo non può aver avuto un inizio, come non può avere una fine. Dunque la Creazione è da intendersi come un atto metafisico, fuori dal tempo, che continuamente lo crea (o lo ricrea). Se in questo Platone ha ragione, dobbiamo pensare che dall’eternità esistono l’universo e l’uomo, e dall’eternità esiste questo sapere ermetico, di cui solo oggi l’Occidente prende collettivamente coscienza. Un sapere che di generazione in generazione si tramanda per vie segrete, di cui la storia comune non è quasi mai al corrente e di cui a malapena ha sospettato.

Anche il modo in cui dal Neolitico questa sapienza è giunta fino a noi appare oscuro e difficilmente decifrabile. Sono stati quegli Israeliti che già prima della distruzione del Tempio e della Diaspora si erano trasferiti in Europa a tramandarcelo? Oppure, sono stati i Templari a recuperarlo per mezzo di scavi archeologici o di contatti con eruditi mediorientali, che ancora conservavano i segreti dei costruttori delle Piramidi?

Forse, una risposta certa non l’avremo mai. Ma la risposta alle domande storiche è a questo punto molto meno importante dell’astorica profondità delle verità che oggi ci sono rivelate. Dopo secoli di oscurità le intime proporzioni dell’universo e della Mente Divina ritornano in possesso dell’uomo, che finalmente trova prova certa che il cosmo, lungi dall’essere dominato dal Caos, è dominato da un ordine armonico, le cui meravigliose trame si estendono dall’infinitamente grande all’infinitamente piccolo, e il cui specchio è la struttura del Numero, immagine dell’Intelligenza Divina e dunque anche di quella umana, che i moti del pensare divino è capace di intendere.

Si svelano dunque come un mito decadente le teorie evoluzioniste, che vedono il mondo dominato da un caso senza volto e senza destino. Finalmente l’abisso che ha diviso la conoscenza scientifica da quella spirituale è colmato. Possiamo adesso essere scienziati e matematici senza perciò mettere da parte la nostra fede. Anzi, d’ora in avanti essa potrà trovare alimento e fondamento proprio in quelle scienze che fino a qualche anno fa si credeva che fossero la sua negazione.

Di tutto questo dobbiamo essere grati alle grandi tradizioni religiose che, pur fra mille contraddizioni, sono state capaci di tramandarci quel codice mitico-astronomico che Giorgio de Santillana e Ertha von Dechend sono stati capaci di decifrare, e di cui oggi possiamo misurare tutta l’immisurabile altezza, ampiezza e profondità, tanto sul piano fisico, che su quelle matematico, che su quello metafisico.

Ci serva questo per fare un bagno di umiltà. Ci serva questo come avvertimento per il futuro delle nostre ricerche scientifiche, storiche e archeologiche. Quando ci volgiamo a testi come i Veda, o la Bibbia, facciamolo con la reverenza e l’umiltà di chi si volge all’insegnamento di grandi maestri, e non con il disprezzo di chi si crede la punta di lancia di un’evoluzione che, fra i molti difetti di cui è stata portatrice, ha ameno avuto il grande pregio di non esserci mai stata. Di fronte ai capolavori del passato, mettiamoci dunque nella posizione di chi chiede ed ascolta. Le pagine che abbiamo appena finito di leggere ci dimostrano chiaramente che abbiamo tutto da guadagnarci.

Capitolo 11:

ALTRE PROBLEMATICHE CONNESSE ALL’INTERPRETAZIONE ARCHEOASTRONOMICA DEL PLATEAU DI GIZA: LE TEORIE DI ANDREW COLLINS IN RELAZIONE ALLA SEZIONE AUREA DEL SEMICICLO PRECESSIONALE INDIVIDUATA DAI POZZI STELLARI DELLA PIRAMIDE

1.

Probabilmente, la teoria archeoastronomica più seria e complessa che negli ultimi anni è stata proposta come alternativa a quella di Bauval è quella di Andrew Collins. Questo archeologo inglese, anche sulla base dell’imprecisione dell’allineamento di cui abbiamo parlato all’inizio della prima parte, sostiene che in realtà le tre Piramidi di Giza non furono allineate con Orione nel 10500 a.C., ma bensì con il Cigno. Vediamo qui sotto altre due immagini, dopo quella che abbiamo già mostrato e fra le molte che potremmo mostrare, che prendono nota di questo errore. Un errore che dipende anche dal programma computerizzato con cui il cielo del 10500 a.C. viene di volta in volta ricostruito

Invece, l’allineamento indicato da Collins si è verificato in un’epoca attorno al 2500 a.C., e coincide perciò con la data indicata dai Pozzi Stellari della Camera del Re e della Regina. E Collins ritiene, con un certo fondamento c’è da dire, che questa collimazione rappresenti una conferma di grande peso della sua ipotesi.

La correlazione con il Cigno, secondo Collins, è anche maggiormente esplicativa di quella sostenuta da Bauval, dato che è capace di dare un senso archeoastronomico anche ad altre due strutture poco studiate, o addirittura del tutto ignorate, tanto dall’egittologia tradizionale che da quella alternativa. La prima è un pozzo che si trova a Gebel Gibli (che è quello che, nell’immagine sottostante, vediamo andare a sovrapporsi ad Alberio, la testa del Cigno). La seconda è la cosiddetta “Tomba degli Uccelli”, un tempio dove erano conservate le mummie di uccelli, presumibilmente divinizzati.

Collins sostiene che da questo tempio si dipartirebbe, in direzione del pozzo di Gebel Gibli, una vasta caverna, da lui personalmente esplorata. Questa caverna, nel 2500 a.C. andava a collimare perfettamente con il corpo del Cigno. Ma – ahimè – di tale scoperta, che sembra davvero del massimo rilievo, è stato impossibile avere altre testimonianze che i filmati girati dallo stesso Collins durante le prime esplorazioni. Infatti, Zahi Awass, massimo responsabile archeologico di Giza, avvertito immediatamente da Collins della scoperta, lo ricompensò generosamente della sua professionalità e della sua lealtà proibendo poco dopo qualsiasi ulteriore indagine, sia sul tempio, sia sulla caverna che da esso si diparte.

Collins però, non si è accontentato della correlazione astronomica, e ha rafforzato le sue tesi con vaste argomentazioni di tipo storico-antropologico, che sembrano abbastanza convincenti, almeno per chi crede nell’importanza dell’astronomia nelle religioni del Paleolitico e del Neolitico. Nel suo best seller “The Cygnus Mystery” Collins sostiene infatti che nel passato ancestrale dell’umanità il Cigno fosse un simbolo di fertilità, e che tale fosse considerato anche nell’Antico Egitto. E alle sue argomentazioni, che il lettore può andare a vedere direttamente sul suo sito internet, noi possiamo aggiungerne anche un’altra, che, strano a dirsi, si fonda su alcune ricerche fatte dai sostenitori della teoria rivale.

2.

Infatti, per introdurci a questo problema, noi partiremo da alcune osservazioni che Hancock e Bauval fanno nel loro best seller “Custode della Genesi” intorno a un problema che, secondo noi, è intimamente connesso a quello della correlazione fra la costellazione del Cigno e il paesaggio sacro di Giza e dintorni

Per esempio, ciò che Reymond chiama «la manifestazione della resurrezione del primo mondo sacro», nei testi di Edfu prese la forma di una colonna o di un’asta verticale «la Pertica» su cui era posato un grande uccello, il Falco Divino. A Eliopoli si ergeva un pilastro (Innu, il nome egizio di Eliopoli, in realtà significa «pilastro») su cui si riteneva che un altro uccello «Divino» – il Bennu o fenice – andasse a posarsi. E’ interessante che il geroglifico di Eliopoli – una colonna sovrastata da una croce sopra (o accanto) a un cerchio diviso in otto parti – sia di fatto identico a un geroglifico che illustra la «Pertica» di Edfu riprodotta da Flinders Petrie ne suo Royals Tombs of the Earliest Dynasties.

G. Hancock, R. Bauval, Custode della Genesi, TEA, 1997, p. 261

E’ del tutto possibile – anzi, secondo noi molto probabile – che questo Falco Divino o Fenice che periodicamente si posa sulla pertica non sia altro che la Costellazione del Cigno, che si trova vicinissima al cerchio tracciato nel cielo del Nord dal movimento precessionale della Terra, come possiamo vedere nell’immagine sottostante. Ma, ben più importante di questo, sembra il fatto che se uniamo Thuban ( cioè la stella polare che viene “centrata” dall’asse polare terrestre nel 2500 a.C.) con la Testa del Cigno, vediamo che il cerchio della precessione viene diviso esattamente a metà. Questo significa che un semiciclo precessionale si è compiuto dal momento in cui l’asse polare gli ha “sfiorato” la Testa a quello in cui – attorno al 2500 a.C. – le sue Ali vanno a collimare con le tre Piramidi di Giza

Ora il cielo nell’Antico Egitto era considerato una divinità femminile, il cui nome era Nut. Nella rappresentazione che qui sotto, vediamo che la costellazione del Cigno corrisponde con discreta precisione al suo utero

Sembra dunque possibile che, quando il ciclo precessionale portava l’asse della Terra a passare vicino alla testa di questa costellazione, questo doveva segnare l’inizio di un nuovo ciclo, non direttamente sincronico con quello segnato a Giza da Orione. Dunque, il significato del mito della Fenice che rinasce dalle sue ceneri, o quello del Falco Divino che si posa sulla Pertica (cioè sull’asse polare della Terra) dovrebbe essere riferito al ciclo e al semiciclo precessionale misurati per mezzo della costellazione del Cigno e della stella polare Thuban.

Invece, come ben sanno i sostenitori e i conoscitori delle teorie di Bauval, quello misurato per mezzo di Orione, viene segnato dall’entrata del Sole nel segno del Leone all’alba dell’equinozio di primavera. Questo momento corrisponde al punto più basso raggiunto da Orione sul meridiano di Giza (l’ultima volta che questo evento si è verificato è stato nel 10.500 a.C. come ha spiegato Bauval in “Il Mistero di Orione” e in “Custode della Genesi”). Sul punto opposto del cerchio precessionale, troviamo che la culminazione di Orione si verifica invece in connessione con il momento in cui l’asse polare della terra va a “centrare” la stella polare attuale, Polaris. Questo accadrà nel 2300 d.C. circa, come possiamo vedere nell’immagine sottostante. E qui sembra importante sottolineare che unendo Polaris con il Polo dell’Eclittica, si traversano due stelle della testa del Drago, prima di andare a centrare una data che si situa appunto attorno al 10.500 a.C.

3.

Che per mezzo del Cigno e del suo allineamento sulle tre Piramidi maggiori di Giza si possano misurare tanto il ciclo che il semiciclo precessionale sembra dare ancora maggior consistenza alle tesi di Collins, senza togliere nulla a quelle di Bauval. Infatti, questi due semicicli precessionali ricavati per via astronomica, come vedremo andando avanti nel lavoro, stanno fra di loro in un sistema di rapporto matematici fondati su quegli stessi numeri sacri, π, ɸ, il 10 e il numero di Eulero, che vennero codificati nelle misure della Grande Piramide già a partire da quella del suo lato misurato in cubiti.

Il 2500 a.C., data in cui le tre Piramidi, il tempio e il pozzo diventano un’immagine celeste del Cigno, è anche la data in cui i Pozzi Stellari vanno a “inquadrare” Sirio, Alnitak, Kochab e Thuban. Ma, come abbiamo dimostrato in The Snefru Code parte 5 questa non è una data qualsiasi, destinata a perdersi nell’infinità insignificante di un tempo lineare irripetibile, proteso verso la morte termica dell’universo. Essa si riferisce alla sezione aurea di un tempo eternamente ritornante, ovvero di quell’altro semiciclo precessionale, quello che viene segnato dal gigantesco pendolo cosmico che Orione idealmente rappresenta sul meridiano di Giza.

Per introdurci a questo argomento, profondamente connesso con il ruolo decisivo che ebbe il numero d’oro nella cultura scientifica, religiosa e filosofica Antico Egizia, possiamo cominciare col ricordare che in “The Orion Mistery” – parlando del significato astronomico del pozzo Sud della Camera del Re – Bauval spiega che la culminazione di Alnitaki sul meridiano era – dal punto di vista di un osservatore posizionato a Giza nel 2500 a C. – di circa 45°. Oggi il punto di culminazione si trova a 58°06, cioè ben 13°06 più in alto. Però non siamo arrivati ancora al punto massimo, che sarà raggiunto nel 2400 d.C. circa, e sarà di 8’ superiore, pari cioè a circa 58°14’ = 58°,23333..

E qui possiamo notare che il rapporto fra i 45° del 2500 a.C. con i 58°,233.. della prossima culminazione è enormemente significativo dal punto di vista simbolico e matematico, dato che esso è molto vicino a √π_Cheope – 1, e che la differenza con il numero esatto è pari all’incirca a (√π_Cheope + 4) ∙ 10^-5

45° : 58°,233333.. = 0,772753291.. ≈ √π_Cheope – 1 = √22/7 – 1 = 0,77281052.. (-5,7229.. ∙ 10^-5 ≈

≈ (√π_Cheope + 4) ∙ 10^-5 = 5,772810.. ∙ 10^-5

Ma, oltre a questo, dobbiamo notare inoltre che l’angolo di 58°14′ corrisponde in modo quasi perfetto all’angolo opposto al cateto maggiore di un triangolo rettangolo i cui cateti abbiano una misura pari alla sezione aurea. Un tale triangolo ha il cateto maggiore pari a 1/ɸ = 0,618033… e uno minore pari a 1/ɸ² = 0,381966… Date queste misure dei cateti l’angolo opposto al cateto maggiore risulta appunto di circa 58°14’ (per la precisione, circa 58°16′).

Dobbiamo quindi concludere che Giza venne scelta come luogo della costruzione delle tre Piramidi anche perché in quel punto la culminazione di Orione raggiunge il massimo lungo la direzione di un angolo che appartiene a un triangolo rettangolo costruito sulla sezione aurea.

Questo dato ci conferma per l’ennesima volta non solo la quasi fantascientifica abilità degli architetti e degli astronomi Antico Egizi, ma anche l’enorme importanza che ebbe per loro il numero d’oro in ogni dettaglio delle loro costruzioni. Tanto che a questo punto sembra del tutto logico che l’orientamento dei Pozzi Stellari segni una data che non è altro che la sezione aurea del semiciclo precessionale, iniziato nel 10500 a.C. (cioè quello caratterizzato dall’entrata del Sole nel segno del Leone e dal punto più basso raggiunto da Orione sul meridiano di Giza all’equinozio di primavera).

Come abbiamo detto sopra, la posizione delle tre Piramidi sul Plateau di Giza rispecchia appunto la posizione delle stelle della Cintura di Orione al 10500 a.C. circa, mentre i Pozzi Stellari della Grande Piramide mirano alla posizione raggiunta da Sirio, Alnitak, Thuban e Kochab in una data attorno al 2500 AC. Scartabellando fra i molti tentativi di datazione “esatti” si può trovare fra l’altro un “circa 2465 AC” che sembra in questo senso particolarmente interessante. Infatti, se facciamo la differenza fra questa data e quella indicata dai Pozzi Stellari, troviamo che 10500 – 2465 = 8035 anni. Ma se adesso calcoliamo la sezione aurea della durata della metà di un ciclo precessionale (cioè del tempo impiegato da Orione per arrivare dal minimo al massimo sul meridiano di Giza e viceversa), vediamo che 13000 ∙ 0,618033.. = 8034,429 (ricordiamo 13000 anni è il tempo occorrente a una stella per oscillare dal massimo al minimo all’orizzonte e viceversa).

Scopriamo così che quella che credevamo una data riferita ad un momento storico unico e irripetibile – la data cioè della costruzione della Grande Piramide – si riferisce in realtà a un momento eternamente ritornante del ciclo precessionale, inteso come un Anno Divino. Nel 2465 a.C. Osiride-Orione aveva toccato il punto aureo della sua ascesa nel cielo a sud di Giza.

Un’altra chiarissima allusione al ciclo precessionale è contenuta anche nelle misure del primo tratto dei quattro Pozzi Stellari, che misurano 52 centimetri quadri di sezione per 180 di lunghezza. Queste misure danno luogo a un volume pari 9360 centimetri cubici, che, a livello numerologico, corrispondono a 26 volte un anno solare “puro” di 360 giorni, con il 26 che contiene un ovvio riferimento al ciclo precessionale (26000 anni di 360 giorni ciascuno sono costituiti da un totale di 9360000 giorni).

4.

E qui conviene forse soffermarci con un inciso sulla sezione aurea del semiciclo precessionale, ovvero, in ultima analisi, sulla sezione aurea del 13. Il motivo è che da essa possiamo ricavare una serie di considerazioni di tipo prettamente matematico – legate a ɸ e π e alle approssimazioni che di questi numeri sacri furono codificate nella Grande Piramide – che ci sembrano di interesse troppo alto per essere trascurate. Si tratterà di un lavoro lungo e complesso, che sul momento potrà anche sembrare una digressione di dubbia utilità, per non dire una labirintica distrazione dall’argomento principale, che appare al tempo stesso molto più semplice e molto più affascinante: il significato archeoastronomico del Plateau di Giza.

Ma il compito di questo lavoro non è in primo luogo quello di affascinare, o di divertire, ma quello di comprendere, e di comprendere fino in fondo quella cultura a noi tanto distante che ha costruito quel complicatissimo paesaggio sacro che è il Plateau di Giza. E la comprensione approfondita di una cosa semplice e affascinante, come la scoperta che i Pozzi Stellari della Camera del Re e della Regina puntano alla sezione aurea di un semiciclo precessionale, implica il prendere di nuovo in considerazione – almeno parzialmente – il lavoro che abbiamo fatto nella prima parte riguardo al ciclo scoperto da Charles Marcello.

Infatti, attraverso il lavoro che svolgiamo noi non dobbiamo solo dimostrare questa o quella affermazione quanto al significato astronomico o matematico di questa o quella costruzione, di questa o quella raffigurazione. Dobbiamo invece diventare capaci di comprendere la connessione universale di ogni parte con ogni altra parte e con il Tutto: in questo caso, la connessione fra un momento sacro – cioè festivo – dell’Anno Divino, individuato dalla sua sezione aurea, con la scienza matematica in grado di comprendere l’Universo e prevederne i moti. Le leggi fisiche che di quel ciclo cosmico scandiscono l’eterno ritmo sono al tempo steso la ragione della scelta di Giza come luogo di costruzione della Meridiana Precessionale che quel ciclo cosmico è destinata a misurare, la ragione della collocazione di ogni pietra in quel luogo in cui è stata collocata, le ragioni delle sue misure e del metodo e della precisione con cui è stata scelta e lavorata.

L’essenza della cultura Antico Egizia è infatti il monofisismo: ovvero la scoperta che tutto si lega con tutto, ch il Tutto e le sue parti scivolano l’uno nell’altro senza posa. E il simbolo ermetico precipuo di questa possente visione metafisica è proprio la matematica, l’infinità plasmabilità del numero, le sue infinite potenzialità di trasmutazione che sono poi la Χώρα (Chôra), ovvero quel “ricettacolo invisibile e senza forma…dell’intero divenire” cui Platone allude nel Timeo. Quando vediamo una scena religiosa come questa qui sotto – in cui Ramses offre fiori alla dèa Sekhmet – pensiamo a riti, preghiere, incantesimi, usi e costumi alieni che, ad esser buoni, possiamo giudicare delle superstizioni esotiche e dunque piene di fascino

Poi però scopriamo che questa stele è stata costituita a partire da una matematica e da una scienza enormemente più evolute della nostra, su cui solo oggi siamo in grado di alzare l’enigmatico velo. Ce lo dimostrano le connessioni geometriche fra questa stele e quel diagramma dello spazio tempo – elaborato da Zappalà che è in grado di rendere ragione della geometria della Piramide e di tutta l’arte sacra antico Egizia

La nebbia di pregiudizi che incombe sulla cultura del Paleolitico, che la vuole come un primitivo balbettare di scimmie che hanno appena smesso di grugnire, è talmente spessa che si ha continuamente bisogno di ricordare, in primo luogo a sé stessi, la quasi smisurata raffinatezza del sistema scientifico- matematico con cui abbiamo a che fare. Questo significa che ogni volta che scopriamo una relazione, che so, fra un monumento e un ciclo cosmico, dobbiamo ben tenere a mente che questa relazione, oltre a non essere frutto di un caso, fa parte di un complesso organico di altre relazioni che stanno fra di loro come le singole note stanno all’armonia, e come la singola armonia sta al complesso sinfonico cui apparitne. Dunque, via via che andiamo avanti, sarà bene farci un’idea, per quanto embrionale, dell’enorme complessità del significato matematico di un’espressione come “sezione aurea del 13”, che la nostra matematica da molto semplicisticamente per scontata. Senza sospettare minimamente quel che possa al tempo stesso rivelare e nascondere. Senza neppur tentare di immaginare quello che poteva significare per i sacerdoti-astronomi che l’avevano fissata per mezzo di una disposizione di giganteschi monumenti talmente accurata che richiederebbe tecniche di tipo atomico-astronautico per essere da noi ripetuta.

5.

La sezione aurea, o numero d’oro, o proporzione divina, non era con ogni evidenza per queste genti quel numero dalle particolarità tanto curiose, ma per altro verso del tutto inutile e indifferente che è per i nostri fisici e i nostri matematici. Esso era per loro quel che fu per Keplero, uno degli ultimi eredi del pensiero ermetico-paltonico: una parte della Mente Divina, una proporzione fondamentale di cui Dio si era servito per generare il cosmo. Dunque un numero sacro, e tenuto gelosamente segreto come un “mistero”.

Ma in The Snefru Code parte 9 abbiamo scoperto che, in un certo senso, π e ɸ possono essere considerati quasi la stessa cosa, dato che entrambi si possono derivare con approssimazione vicina al milionesimo da un numero – il Numero di Cheope – vicinissimo alla sezione aurea del 3, per mezzo di un’operazione matematica che abbiamo chiamato potenza-specchio, in cui un numero viene elevato alla potenza di sé stesso (per esempio, 2 al quadrato possiamo considerarlo in questo senso come una potenza-specchio, e la radice quadra di 4 come una radice-specchio, dato che il suo risultato coincide con il suo esponente).

Avevamo allora ipotizzato che il 3, in grazia di questa possibilità di creare un rapporto strettissimo con ɸ e π potesse essere considerato in questo senso un numero altrettanto sacro che π e ɸ.

E qui possiamo trovare una conferma di questa nostra tesi, dato che adesso ci apprestiamo a scoprire che la sezione aurea del 13 – cioè di un altro numero primo, proprio come il 3 – ha una strettissima e finora del tutto insospettata relazione con π. Infatti, se dividiamo il prodotto fattoriale di π per quello del suo inverso, quello che otteniamo è appunto un’approssimazione della sezione aurea del 13, da cui possiamo ricavare un valore vicinissimo a ɸ_Cheope.

π ! : 1/π ! = 3,141592.. ! : 0,318309.. ! = 7,18808.. : 0,894863.. = 8,032599.. ≈ 13/ɸ = 8,034441..

13 : (π ! : 1/π !) = 1,618405.. ≈ ɸ_Cheope = 1,618590.. (-1,853089.. ∙ 10^-4 ≈ 3/ɸ_Cheope ∙ 10^-4 = 1,8534.. ∙ 10^-4

Questa connessione così intima fra ɸ e π, che trovano un intimo punto di contatto per mezzo di un numero sacro quale il 13 – il settimo membro della serie di Fibonacci escludendo lo 0 – sembra già di per sé qualcosa di notevole. Essa sembra far sistema con il Numero di Cheope e la sezione aurea del 3. Infatti, la differenza fra 13 e 3 è 10: vale a dire uno dei numeri sacri che furono codificati nel lato della Grande Piramide, insieme a π, ɸ e al numero di Eulero. E proprio come da π si può ricavare 13/ɸ_Cheope, dal 10 possiamo ricavare 2/ɸ_Cheope per mezzo del suo stesso logaritmo naturale, cioè per mezzo del numero di Eulero

³√[10 : (Ln 10)²] = ³√1,886116970.. = 1,235538.. ≈ 2/ɸ_Cheope = 1,235643.. (-1,048.. ∙ 10^-4

Per di più, la sezione aurea del 13 ha un’altra caratteristica che sembra notevolissima. Infatti il risultato della sezione aurea di qualsiasi numero della serie di Fibonacci, che ha come limite il numero d’oro, è il numero precedente della serie. In questo caso, facendo 13/ɸ, passiamo dal settimo numero al sesto, ovvero l’8, più un resto decimale, che nel caso del 13 è quello che vediamo qui sotto

13 : ɸ = 8,0344418537486330266596288467533

8,0344418537486330266596288467533 – 8 = 0,0344418537486330266596288467533

Ebbene, questo resto decimale è la x in grado di soddisfare all’equazione armonica che vediamo qui sotto, il cui risultato coincide con ɸ⁷. Essa è cosiffatta da individuare quel numero la cui parte decimale è esattamente uguale all’inverso del numero compresa la sua parte intera. Per cui, sottraendo la parte intera e facendo l’inverso, si ritorna interminabilmente al punto di partenza: proprio come in un cerchio. E dunque non c’è da stupirsi se questo particolare “momento” della serie di Fibonacci abbia una stretta relazione con π, cioè, in ultima analisi, con il cerchio

1/x = 29 + x = 29,03444185374863302665962884675 = ɸ⁷

x = 0,0344418537486330266596288467533

Qui dobbiamo notare che il ritornare su sé stesso come in un cerchio è una caratteristica che unisce tutte potenze dispari di ɸ che, via via che crescono di entità, diventano sempre più vicine a un numero intero e hanno un decimale sempre più piccolo. Le potenze pari invece, sommate al loro inverso, danno il numero intero successivo a quello che si è ottenuto con la potenza. Per esempio

ɸ⁸ + 1/ɸ⁸ = 46,97871376374779181229632352167 + 1/46,97871376374779181229632352167 =

= 46,97871376374779181229632352167 + 0,0212862362522081877036764783216 = 47

Rimane però il fatto che questa caratteristica della sezione aurea del 13, anche se è comune a tutte le potenze dispari ɸ – come anche ad altri numeri – rimane comunque sia altamente simbolica del cerchio della precessione, destinato a ritornare per l’eternità al su sé stesso come le potenze dispari di ɸ.

Inoltre, ɸ⁷ si inserisce perfettamente nel ritmo dei numeri che mettono in connessione quasi diretta π e ɸ che, come abbiamo visto, sono il 10 e il 3, che sommati danno 13, ma la cui sottrazione dà appunto 7.

In secondo luogo, possiamo osservare che in connessione con la caratteristica “ciclicità” del numero vi è senz’altro anche il fatto che se lo dividiamo per la sua parte decimale otteniamo il numero stesso elevato al quadrato; invece, dalla moltiplicazione otteniamo lo stesso risultato che dalla sottrazione, ovvero 1.

29,034441853748.. : 0,034441853748.. = 29,034441853748..² = 842,998813.. = ɸ¹⁴

29,034441853748.. ∙ 0,034441853748.. = 29,034441853748.. – 0,034441853748.. = 1 = ɸ – 1/ɸ

Tutti questi numeri fanno ovviamente parte di quella grande famiglia che abbiamo visto in The Snefru Code parte 11 e parte 12. Ovvero di quei numeri a cui, sottraendo il numero inverso, ci danno un numero intero. Abbiamo già individuato alcune loro caratteristiche particolari, quali la possibilità di ricavare tutti i numeri pari da radici di numeri dispari. Adesso sappiamo che possiamo ricavare almeno alcuni di quelli dispari da potenze dispari del numero d’oro.

6.

Queste strane proprietà di ɸ⁷ = 29,0344.., come abbiamo visto, sono comuni a tutte le potenze dispari di ɸ. In questo senso, il 29 non differisce da altri numeri. Per altro verso, il 29 sembra assumere però un tratto di unicità perché sembra in qualche modo connesso al prodotto di ɸ per il suo prodotto fattoriale ɸ!. In pratica, se facciamo [(ɸ ∙ ɸ!) – 2] : 10, troviamo un’approssimazione di 1/29,

[(ɸ ∙ ɸ!) – 2] : 10 = 0,03449027539751844612648410073307 ≈ 1/29 =

= 0,03448275862068965517241379310345 (+0,00000751677682879095407030762962

Abbiamo scritto per intero il valore della differenza con l’esatto valore di 1/29 perché in questo caso sembra trattarsi di un valore che piuttosto significativo. Infatti, se facciamo la radice 32sima del suo inverso, troviamo un’approssimazione straordinariamente buona del prodotto fattoriale di ɸ. E questo, di riflesso, sembra garantire al 13 e perciò anche al semiciclo precessionale misurato dai Pozzi Stellari della Camera del Re e della Regina – dalla cui sezione aurea ricaviamo ɸ⁷ – un momento di unicità rispetto a ɸ che altri numeri invece non sembrano avere

³²√1/0,00000751677682879095407030762962 = ³²√133035,74427935308611850152485443 =

= 1,4458525681827576604612052030228 ≈ ɸ! = 1,4492296022698966003778797906298 (-0,003377..

Il 13 sembra avere in questo senso, qualcosa come un particolare “dono matematico”, dato che se facciamo la radice di 171, quello che troviamo è di nuovo un “numero ciclico”, la cui parte intera è di nuovo corrispondente a 13, che rimanda a un 26 più una parte frazionaria che riporta al 13 di partenza. È quella stessa caratteristica che abbiamo scoperto esser tipica del prodotto dei “numeri di Mercurio”, che ci porta a dei numeri sacri che – come il 13 e il 26 – che erano sacri nella cultura Maya – rimandano continuamente l’uno all’altro per mezzo della loro parte decimale. In questo caso particolare però vediamo che il rapporto fra questi numeri è esattamente pari a 2

√171 = 13,076696830622020656710945951579

1/(13,076696830622020656710945951579 – 13) = 26,076696830622020656710946225812

1/(26,076696830622020656710946225812 – 26) = 13,038348415311010328355426356575

26,076696830622020656710946225812 : 13,038348415311010328355426356575 = 2

Troviamo qui una nuova conferma di una struttura nascosta che attraversa come una sorta di segreta rete neuronale tutti numeri. Qui vediamo che la radice quadrata di un numero dispari, che apparentemente non ha proprio nulla di diverso da tutti gli altri numeri dispari, in un modo complesso ci rimanda all’archetipo di tutti i numeri pari. E, come vedremo in un lavoro successivo, sarà proprio la frazione decimale di 171, vale a dire 171/10 = 17,1 a essere scelta come l’architrave matematico della Piramide di Djoser.

Abbiamo sopra ricordato che questa caratteristica di √171 ci rimandava a quelle possedute dai “numeri di Mercurio”. Essi si connettevano con tre dei numeri del codice astronomico sacro individuati da de Santillana e von Dechend, così che abbiamo scoperto che tale codice va molto più in là di un generico riferimento al ciclo precessionale: esso si riferisce infatti a una struttura matematica che percorre anche tutti gli altri rapporti che danno origine al sistema solare. Infatti, il prodotto dei “numeri di Mercurio” ci dava 59 ∙ 88 = 5192. La sua radice ci portava a quel fantastico rimando ciclico fra numeri sacri che abbiamo visto sopra, ma che conviene rivedere qui sotto

√5192 = 72,05553413860728574149502756704

1/(72,05553413860728574149502756704 – 72) = 18,00694176732591071768687844588

1/(18,00694176732591071768687844588 – 18) = 144,05553413860728574149502756704

1/(144,05553413860728574149502756704 – 144) = 18,006941767325910717686878444248

7.

Il lettore noti che ci stiamo muovendo come in un cerchio. O meglio: come in un sistema di cerchi. Dalla sezione aurea del 13, che altro non è che un’idealizzazione della sezione aurea di un semiciclo precessionale, cioè del ciclo cosmico fondamentale – l’Anno Divino – siamo rimandati a un numero che, oltre a rappresentare la durata di un giorno precessionale, come abbiamo visto nella prima parte, caratterizza, per esempio, il rapporto fra la durata del periodo di Mercurio attorno al Sole e attorno a sé stesso. Un numero che poi ritroviamo di nuovo, se facciamo il prodotto fattoriale di ɸ⁷ e lo interpretiamo numerologicamente come un seno iperbolico. A questo punto, scopriamo che l’angolo connesso è, nella sua parte intera, di nuovo il magico 72. E si nota che il resto decimale è una discreta approssimazione della costante gravitazionale G divisa per 10²

sinh x = 29,034441853748633026659628846753 ! = 9935086639263923029729517588782,2

x = 72°,06677.. ≈ 72° + G/10² = 72°,06672

Invece, se del prodotto fattoriale di ɸ⁷ ne facciamo il logaritmo in base 10, quella che troviamo è una buona approssimazione di π³

³√log 9935086639263923029729517588782,2 = ³√30,997171.. = 3,141285.. ≈ π = 3,141592..

E qui dobbiamo riprendere una questione che ci siamo posti all’inizio di The Snefru Code parte 11, perché ci accompagni nel seguitare delle nostre riflessioni: la piramide del sapere può essere assimilata alla sfera di Ermete Trismegisto, ed essere definita come una piramide la cui punta è ovunque è la cui base è in nessun posto? Quel codice astronomico sacro individuato da de Santillana e von Dechend è un fondamento del sistema matematico con cui Dio ha generato l’universo oppure si fonda sul sistema trigonometrico a base 360? Ma abbiamo visto che il sistema trigonometrico a base 360 si fonda o pare fondarsi a sua volta sui quattro numeri sacri codificati nelle misure della Piramide già a partire dal suo lato, ovvero su π, ɸ, il 10 e il numero di Eulero. Ma questi numeri, come abbiamo visto, formano un sistema di approssimazioni che in certi casi li porta fin quasi al punto di scivolare l’uno nell’altro, di confondersi l’uno con l’altro!

Per dare un’idea del cerchio in cui ci troviamo, possiamo far notare che l’approssimazione di 13/ɸ che sopra abbiamo ricavato da π ! : 1/π !, che va molto vicina a ɸ_Cheope: questo vuol dire che la sezione aurea del ciclo precessionale, scandita dall’orientamento dei Pozzi Stellare della Piramide, rimanda in modo ermetico a quell’approssimazione particolare di ɸ con cui fu costruita.

13 : 8,032599.. = 0,617892.. ≈ 1/ɸ_Cheope = 0,617821

8.

Il lettore ben comprende a questo punto la ragione profonda e dunque l’assoluta indispensabilità di queste nostre “digressioni” verso la matematica pura. Il fatto è che quando parliamo di un luogo come Giza stiamo parlando di un capolavoro di architettura sacra eseguito da misteriosi personaggi – che noi chiamiamo “Antichi Egizi” – i quali nel sancta santorum della loro fede conservavano come elemento forse più prezioso la matematica con cui Dio ha generato l’universo. Lungi dal far parte di una conoscenza di rango inferiore – come in Aristotele – o di un dominio “laicizzato” – come avviene oggi in Occidente – una scienza come la fisica era parte essenziale della conoscenza di un universo sentito come integralmente sacro: cioè come immagine della Divina Intelligenza che l’ha generato.

Quindi, limitare la nostra analisi all’indicazione dei cicli cosmici in esso implicati e ai loro rapporti più esteriori, senza indicare le loro strutturali connessioni con la scienza matematica a cui si è voluto alludere con la loro misurazione, significa di fatto fraintendere l’opera dei maestri Antico Egizi. Significa ascrivere le loro credenze al rango di superstizioni astrologiche, o ridurre l’immensa portata del loro lavoro architettonico e matematico alla costruzione di un “parco di divertimenti per astronomi”, come pure si è avuto il coraggio di scrivere. Quando invece questo grande libro sapienziale scritto con la pietra allude all’essenza divina del mondo, “al numero, peso e misura” con cui Dio ha generato il cosmo.

E infatti, nel terminare la nostra analisi, ecco che scopriamo le connessioni che esistono fra ɸ⁷ e le costanti della scienza empirica. Infatti, la radice cubica di ɸ⁷ ci dà un’ottima approssimazione del numero caratteristico della costante che descrive il diametro classico del protone (d_p = 3,07).

³√29,034441.. = 3,073532.. ≈ d_p = 3,07 (+0,0035326236569833606969800838932

Abbiamo scritto per esteso l’avanzo decimale fra il numero derivato per via astratta da quello derivato per via sperimentale perché da esso possiamo derivare un’ottima approssimazione questa volta del raggio classico del protone (r_p = 1,535)

√[2 + (0,003532623.. ∙ 10²)] = √2,3532623.. = 1,534034.. ≈ r_p = 1,535

Ma, come oramai sappiamo, questa costante rimanda a sua volta alla tangente dell’angolo di 72° (pari a 3,077..). E forse a questo punto non ci stupiremo più nello scoprire che la differenza con i 72° è una funzione di ɸ, approssimata ai milionesimi

tg x = ³√29,034441.. = 3,073532..;

x = 71°,977261534546450836971365497281 ≈ 72° = -0,02273846545354916302863450271867

³√(1 + ⁵√0,0227384..) = ³√(1 + 0,888482..) = ³√(1,888482..) = 1,23605455.. ≈ 2/ɸ = 1,23606797.. (-1,34..∙ 10^-5

Potremmo naturalmente andare avanti e, a partire da queste relazioni, dedurre di nuovo tutte le relazioni che legano il raggio classico del protone con il resto delle grandezze fondamentali dell’atomo. Ma, a questo punto, ci sembra di avere raggiunto il nostro scopo: ovvero quello di dimostrare come ogni parte del sapere sacro che fu codificato a Giza, riguardi esso l’astronomia come la fisica, la geometria o la matematica pura, rimandi sempre e costantemente al Tutto di cui è parte. Quasi a volerci ricordare una proposizione che tutti i cattolici hanno imparato nell’infanzia: Dio è Colui che si trova al contempo dappertutto e in nessun luogo. Ma se si trova dappertutto e in nessun luogo, Egli è al tempo stesso il Tutto e Nulla.

9.

Diciamoci la verità. Chi avrebbe mai sospettato che, partendo dall’orientamento astronomico di una struttura architettonica sacra si potesse arrivare, passando per i cicli eterni che è destinata a scandire, alle proporzioni matematiche con cui la struttura stessa è stata costruita? A chi mai sarebbe venuto in mente che da queste proporzioni si potesse poi passare all’intima struttura della materia, e poi alle relazioni che legano la durata dell’orbita dei pianeti attorno al Sole con il tempo che impiegano a girare su sé stessi? Chi si sarebbe mai sognato che nella matematica e nella geometria platonico-pitagorica si nascondesse una struttura capace di rendere ragione di tutto l’universo, compreso del modo strano in cui i Francesi chiamano 80 e 90?

Novanta, abbiamo visto, si dice “quatre-vingt-dix”, “quattro-venti-10”: dunque, questo sembra un modo di segnalare un rapporto speciale del 90, oltre che con 80, anche con il 20. E in effetti, se facciamo il prodotto fattoriale di 90/20 – e interpretiamo numerologicamente il risultato come un angolo – dobbiamo prepararci a una nuova sorpresa, dato che si tratta di una particolare “sezione aurea” dell’angolo giro

90/20 ! = 4,5 ! = 52°,342777.. ≈ 20 ∙ ɸ² = 52,360.. ≈ 360°/ɸ_Cheope⁴ = 52,451114..

L’approssimazione di ɸ_Cheope che possiamo ricavarne sembra piuttosto buona

⁴√(360°/52°,342777..) = 1,619427215.. ≈ ɸ_Cheope = 1,618590346..

Giunti a questo punto della nostra analisi, forse non c’è nemmeno bisogno di dire che ciò che abbiamo appena visto non può essere considerato affatto un incidente, ma un’ennesima conferma delle caratteristiche armoniche di π, ɸ, del numero di Eulero e del 10, che si riflettono ovunque. Persino dei modi che all’uomo di oggi paiono strani di definire certi numeri sono significativi. Dalla tradizione matematica come da quella numerologica, senza esserne coscienti, sempre o quasi sempre ereditiamo delle suggestioni che ci portano poi a scoprire delle proporzioni matematicamente essenziali e scientificamente profonde. In effetti, chiamare il novanta “quattro-venti-dieci” che altro è, se non un modo ermetico di alludere a quella che abbiamo sopra definito come la struttura organica, armonica dei numeri sacri?

Per fare un altro esempio delle potenzialità armoniche del prodotto fattoriale di questi numeri, che, come vedremo, si lega a un’approssimazione di ɸ che corrisponde direttamente a una costante scientifica, possiamo parlare di quel numero il cui prodotto fattoriale – meno il prodotto fattoriale del suo inverso – ci dà 1, ovvero la x in grado di soddisfare l’equazione che vediamo qui sotto

x ! – 1/x ! = 1; x = 1,93601883..

1,93601883.. ! – 1/1,93601883.. ! = 1,886874.. – 0,516523..! = 1,886874054.. – 0,88687406.. = 1

Ebbene, questo numero, diviso per π, ci dà la lunghezza di Planck meno 1, con una differenza di circa 3 milionesimi

1,93601883../π = 0,616253.. ≈ ℓ_P – 1 = 0,616256..

Se poi ne facciamo per due volte il logaritmo naturale, quello che otteniamo è -√2 + 1, con una differenza che questa volta è di circa 3 decimillesimi

₂Ln 1,93601883.. = -0,414555730.. ≈ -√2 + 1 = -0,414213562..

E qui possiamo scoprire i legami, anche questi molto interessanti, fra √2, ℓ_P e π. Un fatto molto importante dato che π e √2 sono intimamente connessi alla struttura della Piramide, come possiamo dedurre dalla figura sottostante

Il legame fra questi numeri lo scopriamo per mezzo del logaritmo naturale, ovvero, in ultima analisi del numero di Eulero, anch’esso implicato nelle misure della Piramide fin dalla determinazione del suo lato

₂inv. Ln (-√2 + 1) : π = 1,936456586.. : 3,14159265.. = 0,616393.. ≈ ℓ_P – 1 = 0,616256..

√₂inv. Ln [2 ∙ (√2 – 1)] = √₂inv. Ln 0,828427124.. = √9,872118505.. =

= 3,141992760.. ≈ π = 3,14159265.. (+4,001.. ∙ 10^-4

Questo fatto sembra assumere ancora più importanza quando ci rendiamo conto che da √2 – e dunque anche dal seno e dal coseno dell’angolo di 45° della declinazione di Orione sul cielo di Giza nel 2500 a.C. circa, che corrisponde a quella del Pozzo Stellare Sud della Camera del Re – che possiamo ottenere un’ottima approssimazione tanto del numero caratteristico della costante che descrive il raggio classico del protone che il suo diametro classico, e anche di π/2. In quest’ultimo caso, la differenza con il numero esatto, facendo la radice quadrata, corrisponde alla durata del ciclo delle fasi lunari (354,36 giorni) divisa per 10⁴

√[2 + (1/√2)/2] = √2,353553.. = 1,534129.. ≈ r_p = 1,535

-1/√2 ! = 3,067931.. ≈ d_p = 3,07

√2 !² = 1,572053.. ≈ π/2 = 1,570796.. (+0,0012569327..

√0,001256932704.. = 0,035453246.. ≈ 354,36/10⁴ = 0,035436

10.

Questo risultato ci conferma ancora una volta le straordinarie caratteristiche dei numeri connessi con la scienza empirica, che finora avevamo creduto un prodotto di quell’onnipresente e onnipotente Caso che avrebbe portato, oltre che alla nascita della vita sulla Terra, anche alla scelta da parte di una scimmia evoluta del sistema metrico decimale. Ma, vedendo cose di questo genere, chi può più anche solo immaginare che il caso possa avere un ruolo qualsiasi in relazioni come queste che andiamo scoprendo?

Lungi dal trovarci in un mondo dominato dal caso, procedendo alla sua analisi matematica pare proprio che ci troviamo in un Paese delle Meraviglie per noi ancor più inaspettato di quello che Alice trovò seguendo il Coniglio Bianco. I legami che lo attraversano sembrano davvero più magici che matematici, oppure il frutto di una matematica che assomiglia più alla magia dei sogni che a quella fredda “realtà” che il positivismo logico ci ha portato a identificare con al “verità scientifica”. La lunghezza di Planck è una sorta di quanto minimo di spazio, al di sotto del quale il concetto di “distanza” non ha alcun senso fisico. Che cosa ci può entrare una cosa del genere con π, o con √2, o con il modo un po’ strano con cui i francesi chiamano il 70, l’80 e il 90? Eppure, se di 1 + 0,616253.. = ℓ_P facciamo il prodotto fattoriale, in questo modo otteniamo un numero molto prossimo a [(Ln π – 1) ∙ 10]

1,616253933.. ! = 1,447272832.. ≈ [(Ln π – 1) ∙ 10] = 1,447298858.. (-0,0000260264..

Questo, come al solito, sembra già un mezzo miracolo: connessioni tanto esatte fra numeri caratteristici delle costanti fisiche – cioé fra valori derivati da lunghe e faticose ricerche empiriche – con un’entità del tutto astratta ed empiricamente del tutto inspiegabile quale π. E che dire quando poi, di nuovo, come Alice nel Paese delle Meraviglie, passiamo dall’astrazione più radicale alla concretezza che più concreta non è, ovvero al raggio classico del protone? Infatti, possiamo notare che il doppio logaritmo dell’inverso della differenza fra il risultato del prodotto fattoriale di ℓ_P e [(Ln π – 1) ∙ 10] altro non è che il numero caratteristico della costante che descrive il raggio classico del protone (r_p = 1,535) elevato al quadrato

√Ln (Ln 1/0,0000260264..) = √Ln (Ln 38422,516424..) = √2,356732209.. = 1,535165.. ≈ r_p = 1,535

Inoltre, se prendiamo in considerazione il prodotto fattoriale del numero da cui siamo partiti, ovvero 1,93601883.. – cioè la x in grado di soddisfare l’equazione x ! – 1/x ! = 1 – scopriamo che si tratta di un’ottima approssimazione di (2/ɸ)³. Da esso possiamo ricavare di nuovo un’ottima approssimazione di ɸ_Cheope

³√1,93601883..! = ³√1,886874053.. = 1,23570357.. ≈ 2/ɸ_Cheope = 1,235643..

1/(1,23570357.. : 2) = 1/0,617851788993.. = 1,618511134.. ≈ ɸ_Cheope = 1,618590346..

Anche, la x in grado di soddisfare l’equazione armonica che vediamo qui sotto, questa volta connessa a quel numero da cui possiamo ottenere ɸ grazie alla sottrazione fra il suo prodotto fattoriale e il doppio prodotto fattoriale del suo inverso, è a sua volta molto vicina a √5, cioè a ɸ + 1/ɸ. In particolare, il suo valore è ancora una volta un’approssimazione della costante di Planck meno 1

x ! – [1/(x !)] ! = ɸ; x = 2,2328625.. ≈ ℓ_P + (ℓ_P – 1) = 2,232504..

Il valore di questa x lo abbiamo visto anche nella prima parte. Esso è vicinissimo all’inverso di quel numero che sommato al suo logaritmo in base 10 ci dà 0. In questo caso, la differenza che troviamo è un’approssimazione del numero caratteristico della costante che descrive la massa del protone (1,6725) divisa per 10² ed elevata al quadrato. Di nuovo quindi abbiamo un’incursione della realtà sensibile, dell’empiria più pura, nel campo dell’astrazione matematica a sua volta più pura

√(1/2,2328625.. + log 1/2,2328625..) = √(0,399146.. + log 0,399146..) =

= √(0,399146 -0,398867..) = √2,792997.. ∙ 10^-4 = 0,016712.. ≈ m_p/10² = 0,016725

Dunque, a quel che possiamo capire, la matematica divina è onnicomprensiva e non ammette momenti di insignificanza. Non fa differenza fra sistema astratto e realtà. Tutto si connette con tutto per mezzo di approssimazioni che sono significative non solo in sé stesse, ma anche nei resti che troviamo con le cifre esatte, che di nuovo alludono ad altri valori matematicamente e/o scientificamente significativi.

Inoltre, tutte queste equazioni armoniche, pur non essendo coincidenti, tendono a formare degli intorni numerici. Intorni numerici costituiti di numeri irrazionali che, minimamente alterati, ci permettono di passare da una relazione all’altra.

Infatti, anche la x in grado di darci ɸ per mezzo dell’equazione armonica x ! – [1/(x !)] ! = ɸ si lega a alla x che, divisa per il suo logaritmo in base 10, ci dà il numero di Eulero col segno meno

x : log x = -e; x = 0,60102749594626548..

0,60102749594626548.. : -0,221105659337383.. = -2,7182818284590452..

log (10^{0,60102749594626548..} : 10) = log (3,990501661291321.. : 10) = 0,3990501661291321..

0,3990501661291321.. + log 0,3990501661291321.. =

= 0,3990501661291321.. -0,39897250405373452..) = 7,766207.. ∙ 10^-5

11.

Il Cerchio Divino non è solo quello della Precessione. Anche muovendoci nel mondo delle più pure astrazioni matematiche è come se fossimo sempre spinti in un movimento che procede per mezzo del ritorno. Non facciamo in tempo a fare un passo in avanti, ed ecco che ci rendiamo conto di muoverci in un cerchio, o in un sistema di cerchi. O, chissà, forse in un sistema di ingranaggi, ognuno dei quali possiede un numero infinito di denti e che dunque, in questo senso, è assimilabile al cerchio.

Infatti, analizzando la x in grado di soddisfare l’equazione x ! – [1/(x !)] ! = ɸ, subito si nota che 1/(2,2328625.. !) ! = 0,887310622.. è a sua volta molto vicino a (2/ɸ_Cheope)³ – 1. Dunque, anche in questo caso se ne può ricavare una discreta approssimazione di ɸ_Cheope

³√(1 + 0,887310622..) : 2 = ³√1,887310622.. : 2 = 1,23579887.. : 2 = 0,617899.. ≈ 1/ɸ_Cheope = 0,617821..

Il lettore si sarà senz’altro reso conto che questa è l’ennesima volta che ricaviamo ɸ_Cheope o il suo inverso o, comunque sia, una sua funzione, a partire da equazioni che, in linea teorica non ci dovrebbero entrare proprio nulla. Quasi che questo numero fosse una specie di centro invisibile attorno a cui la matematica divina si muove instancabilmente. Ma siccome ɸ_Cheope si può trasformare o essere dedotto anche negli altri 3 numeri fondamentali incorporati nelle misure della Piramide, ecco che questo centro rimane sé anche diventando qualcosa di altro da sé stesso. Il numero d’oro è, simbolicamente, il pentagono. Ma, attraverso la sezione aurea del 3 il numero d’oro può diventare π, e dunque il cerchio. Come in un caleidoscopio, le forme mutano restando misteriosamente le stesse.

Anche la x in grado di soddisfare l’equazione che vediamo qui sotto ci conferma le straordinarie e reciproche potenzialità armoniche di quei numeri che abbiamo individuato come la base della struttura tanto delle misure della Piramide che dell’universo, ovvero il ɸ, π, il numero di Eulero e il 10. Possiamo passare dall’uno all’altro in modi molteplici, anche se la perfezione non è mai raggiunta ma solo sfiorata.

x ! – [1/(x !)] ! = e = 2,718281828..; x = 2,576548295..

2,576548295..! – (1/2,576548295..!)! = 3,619653349.. – 0,901371520.. = 2,718281828.. = e

Anche in questo caso, da 2,576548295..! possiamo ricavare un’ottima approssimazione di ɸ_Cheope, come peraltro dall’inverso del prodotto fattoriale del numero di Eulero possiamo ricavare sia un’approssimazione della lunghezza di Planck che di ɸ_Cheope

√(2,576548295.. ! – 1) = √(3,619653349.. -1) = √2,619653349.. = 1,618534321.. ≈ ɸ_Cheope = 1,618590346..

1/[1 + ³√(1/e !)] = 1/[1 + ³√1/4,260820..] = 1/(1 + ³√0,234696..) =

= 1/(1 + 0,616834..) = 1/1,616834.. = 0,618492.. ≈ ɸ_Cheope – 1 = 0,618590..

Come abbiamo visto altre volte, questi numeri tendono a connettersi, a ritornare su sé stessi, passando molto spesso per il valore di costanti fisiche molto importanti, anche se a volte il gioco sembra avvenire a un livello puramente astratto. In questo senso, sembra particolarmente “spettacolare” il fatto che possiamo ottenere un numero molto prossimo a 10/π_Cheope partendo da ³√π

(³√π)² ! + [1/(³√π)²] ! = 3,181636191.. ≈ 10/π_Cheope = 3,181818..

12.

D’altra parte, il legame armonico fra i numeri che furono codificati nella Piramide e le costanti fisiche sembra una regola. Per esempio, sembra notevolissimo il fatto che il numero capace di soddisfare l’equazione armonica che vediamo qui sotto – da cui possiamo ricavare il valore esatto della velocità della luce – sia un numero che si trova fra π = 3,141592.. e 2 + Ln π = 3,144729.. Il messaggio che possiamo ricavare da queste funzioni è che certi numeri sono come le stelle che vediamo in cielo: sembrano punti, ma non lo sono. Hanno un centro chiaro e luminoso che sfuma in modo tale che il limite che le separa dal buio risulta indefinibile, anche se questo, in un certo senso, non impedisce a nessuno di distinguerlo

x – (³√x)² = c – 2; x = 3,144091..

3,144091.. – (³√3,144091..)² = 3,144091.. – 2,146166.. = 0,99792453.. = c – 2

L’approssimazione di π_Cheope che possiamo ricavare da [(³√π)² ! + [1/(³√π)² !] non è lontana da quella che possiamo ricavare dal prodotto fattoriale di ɸ

10/3,181636191.. = 3,143036.. ≈ π_Cheope = 3,142857.. (+1,797718972522.. ∙ 10^-4

1 + (ɸ !)/10 = 1,144922960.. ≈ Ln π = 1,144792..; e^{1,144922960..} = 3,142199.. ≈ π_Cheope = 3,142857..

Il fatto che ci stiamo muovendo in un sistema simmetrico-armonico, dove nulla, nemmeno i resti decimali delle equazioni viene lasciato al caso, lo conferma per l’ennesima volta il fatto che la differenza fra l’approssimazione di π_Cheope che abbiamo appena ricavato e il numero esatto sia a sua volta l’inverso di un numero molto vicino a Ln π elevato alla 64sima

⁶⁴√1/1,797718972522.. ∙ 10^-4 = ⁶⁴√5562,604.. = 1,144247.. ≈ Ln π = 1,144729..

Capitolo 12:

IL RAPPORTO FRA LE DUE DIVERSE SUDDIVISIONI DEL CICLO PRECESSIONALE INDIVIDUATE DA COLLINS E DA BAUVAL OVVERO LE SUDDIVISIONI DELL’ANNO DIVINO PER MEZZO DI NUMERI SACRI

1.

Dopo il lavoro che abbiamo svolto siamo adesso pienamente consapevoli del profondissimo significato al tempo stesso religioso e matematico-scientifico del paesaggio sacro che stiamo studiando. Dunque, adesso sappiamo di non avere a che fare con un “parco di divertimenti per astronomi”, né con l’opera mezzo meravigliosa e mezzo delirante di astrologi che delle loro superstizioni hanno fatto un monumento. Abbiamo a che fare invece con l’opera di una civiltà avanzatissima, la cui sapienza in questo momento non siamo capaci di misurare nemmeno con l’immaginazione, che attraverso le scansioni del tempo cosmico ha simbolizzato quella divina scienza con cui il cosmo è stato generato.

È vero: nelle testimonianze scritte che questa civiltà ci ha lasciato troviamo cose che a noi sembrano parenti strette delle superstizioni più triviali. Ma ciò che noi disprezziamo in quel che oggi si chiama “astrologia” o “divinazione” non ha nulla a che fare con l’oggetto di quei testi. A quel tempo l’astrologia era una cosa molto seria, e non aveva perciò nulla a che fare con le deprimenti rubriche dei nostri quotidiani, ma bensì con la capacità di antivedere i mutamenti del cielo.

Un esempio di questo genere di profezia lo troviamo, per esempio, nel Prometeo di Eschilo, quando il Titano legato alla roccia profetizza alla Ninfa Io la fine di Giove, che di entrambi i protagonisti della tragedia è stato la rovina

IO:

Come? Giove crollar può dal suo regno?

Promèteo:

Lieta vedendo ciò, credo io, saresti.

IO:

Come no, se per Giove il male io soffro?

Promèteo:

E sappi dunque che tanto avverrà.

IO:

Da chi mai tolto gli sarà lo scettro?

Promèteo:

Da lui stesso: dai suoi consigli stolti.

IO:

Come? Se danno a te non reca, dimmelo.

Promèteo:

Stringerà nozze onde dovrà dolersi.

IO:

Mortali, oppur divine? Se puoi, dimmelo.

Promèteo:

Che importa questo? E dirlo non è lecito.

IO:

Lo sbalzerà dal trono la sua sposa?

Promèteo:

Creando un figlio più forte del padre.

Qui sembra del tutto chiaro che Promèteo (un nome che significa “colui che vede innanzi” ovvero colui che è in grado di fare profezie) sta parlando della fine di un’era cosmica, connessa con Zeus-Giove. Giove sarà ucciso da un figlio più forte di lui, come del resto era successo nelle ere cosmiche precedenti a Urano e a Kronos: Giove stesso, proprio come Edipo, è un assassino del padre. Ciò con cui abbiamo a che fare, in questo come in altri testi antichi, sono mutamenti del cielo descritti in termini mitici: il figlio di Giove è senz’altro una configurazione celeste che, coi mutamenti indotti dalla precessione, acquisterà in qualche modo centralità e preminenza nel cielo, mentre una precedente perderà lo scettro. E qui è difficile capire se il “figlio di Giove” a cui si riferisce Promèteo è una nuova stella polare, o lo scivolare del Sole in un nuovo segno all’equinozio di primavera. La stessa Ninfa Io, trasformata in vacca da Zeus, potrebbe essere null’altro che la costellazione dell’Orsa Maggiore. La sua associazione con figure bovine la troviamo nel poema cosmologico dei Finlandesi, il Kalevala, dove troviamo «una giovenca con le corna tutte splendenti d’oro/

e le stelle dell’Orsa sulla fronte/ il disco del sole appariva sulla sua testa». D’altra parte

La similitudine dei buoi che vengono fatti girare intorno alla macina non è estranea all’Occidente: essa sussiste ancora nelle nostre lingue grazie al latino Septentriones, i sette buoi da trebbia dell’Orsa Maggiore: «che noi siamo soliti chiamare i Sette Buoi» nella traduzione che Cicerone dà di Arato.

G. de Santillana – H. von Dechend, Il Mulino di Amleto, Adelphi, p. 170

Certo, scoprire che una scena tanto piena di pathos tragico come quella che troviamo in Eschilo è riferita a mutamenti che noi consideriamo del tutto indifferenti rispetto alla “realtà” della vita quotidiana, è per noi un fatto piuttosto stupefacente, e ci porta a delle questioni piuttosto imbarazzanti. Soffre forse il cielo stellato nel suo mutare? Patisce una costellazione perché in una certa data, che il tempo cosmico rende banale come tutte le altre, il Sole va a sorgere su un’altra? Non c’è niente da fare. Il nostro atteggiamento integralmente “laico” rispetto al cielo, diurno o notturno che sia, ci rende praticamente impossibile l’identificazione con i protagonisti cosmici di questa scena, a cui siamo portati ad attribuire un qualche significato oscuro, legato a superstizioni o misteri oggi del tutto inaccessibili

Quanto a noi, il sistema copernicano ha spogliato la Precessione della sua solenne grandiosità, facendone una questione puramente terrestre, il barcollare del corso individuale di un pianeta qualsiasi. Ma se si fosse trattato, come appariva un tempo, del comportamento misteriosamente preordinato della sfera celeste o del cosmo nel suo insieme, chi mai avrebbe sfuggire all’emozione astrologica? La Precessione assunse infatti un’importanza preponderante: divenne il vasto disegno impenetrabile del fato stesso, ove un’età del mondo subentrava all’altra, mentre l’invisibile lancetta dell’equinozio scivolava lungo i segni e ogni età portava con sé ascesa e caduta di configurazioni e sovranità astrali, insieme con le loro conseguenze terrene.

G. de Santillana – H. von Dechend, Il Mulino di Amleto, Adelphi, p. 175

Dunque, l’oscurità dell’oracolo non è connessa, come noi siamo inclini a credere, con l’oscurità della mente che la pronuncia, o, peggio ancora, con la sua volontà di ingannare gli ascoltatori per qualche fine pratico. Al contrario, si spiega con il fatto che le culture ermetiche non diffondevano il loro sapere nel modo in cui siamo abituati oggi. I modi di Promèteo, come peraltro anche quelli di Pitagora non sono quelli tipici del manuale scolastico: la metafora prevale sul linguaggio comune, e non c’è peggior fraintendimento di intendere una metafora come linguaggio comune. Quando ci sentiamo raccontare che Pitagora imparò le regole dell’armonia passando davanti alla bottega di un fabbro bisogna avere orecchi per intendere: il fabbro è Efesto-Saturno, non un fabbro qualsiasi, e le regole dell’armonia riguardano in primo luogo quelle sfere cosmiche che abbiamo analizzato nella prima parte del nostro lavoro, non gli strumenti musicali che abbiamo a portata di mano nella vita di tutti i giorni. La figura di Efesto-SAturno in Grecia assomiglia a quella del Saturno cinese, rappresentato come una verde creatura bovina con una gamba sola, di nome Kui

Marcel Granet scrive che l’imperatore Shun nominò Kui «maestro della musica», anzi, ordinò niente di meno che al sole (Chong-li) di prelevarlo dalla boscaglia e di portarlo a Corte: solo Kui infatti, sapeva come armonizzare i sette flauti e i sette modi, e Shun, che voleva pacificare l’Impero, era fermamente convinto che «la musica è l’essenza del cielo e della terra». Kui sapeva anche far danzare i «cento animali» toccando la pietra musicale, e aiutò Yu il Grande, uno dei cinque primi Imperatori e bonificatore instancabile, a compiere l’opera di regolazione dei «fiumi». E si scopre che non solo era Maestro della Danza, ma anche Maestro della Forgia: un compagno davvero eccezionale per Yu il Grande a cui figura di danza (il Passo di Yu) «eseguiva» l’Orsa Maggiore.

G. de Santillana – H. von Dechend, Il Mulino di Amleto, Adelphi, p. 157

In questo senso, Giza, in quanto Meridiana Precessionale, è una sorta di Promèteo o di Pitagora di pietra, in grado di prevedere il futuro e di insegnarci l’armonia delle sfere: cioè la scienza in grado di descrivere, fra l’altro, anche i mutamenti del cielo connessi con il ciclo precessionale, che furono accuratamente suddivisi in base alla geometria suggerita dal cielo del Nord. E un indovino di pietra pronuncia col suo silenzio oracoli che sono dunque per certi versi più oscuri di quelli del Titano che rubò il fuoco agli dèi o della caligine di leggende che attornia il filosofo che non lasciò scritta una sola parola del suo pensiero e che probabilmente non è neppure mai esistito. Anche il fuoco che Promèteo rubò agli dèi non è da intendersi come quello del caminetto. Promèteo, come Pitagora, ha rubato agli dèi il fuoco della conoscenza, che, come per il resto sostiene anche il Platone del Timeo, trova nell’astronomia la sua prima origine.

2.

Il fuoco della conoscenza, e dunque dell’astronomia, arde a tutt’oggi arde in modo accecante sul Plateau di Giza: il Tempo è il suo nutrimento, e per questo non è capace di spegnerlo. Nella parte precedente di questo lavoro abbiamo individuato due diverse possibili suddivisioni a metà del ciclo precessionale. L’una, quella inconsapevolmente individuata da Collins, va dalla Testa del Cigno a Thuban. L’altra consapevolmente individuata da Bauval, va dall’entrata del Sole nel segno del Leone all’equinozio di primavera – epoca che coincide con il punto più basso di Orione sul meridiano di Giza – fino al momento in cui l’asse polare della Terra andrà fra circa 300 anni a centrare perfettamente Polaris, cosa che avverrà in coincidenza con la culminazione di Orione.

Questi due cicli trovano un punto d’incontro nel 2500 a.C. indicato dai Pozzi Stellari. Una data che non coincide affatto, come finora si era creduto, con quella in cui fu costruita la Grande Piramide, ma con un passaggio cruciale nel corso di quell’anno divino che per gli antichi era il ciclo precessionale. Un passaggio corrispondente con la sezione aurea di un semiciclo precessionale, pari a 13000 : ɸ = 8034 anni circa. Ovviamente, questo significa fra il momento in cui l’asse polare della Terra va a sfiorare la Testa del Cigno e quello in cui il Sole entra nel Leone, vi è un periodo di tempo corrispondente a circa 13000 : ɸ² = 4965,55 anni.

Se il 10500 rappresentava la fine del vecchio ciclo precessionale e l’inizio del nuovo (ovviamente, usando come punto di riferimento Orione al minimo e l’entrata del Sole nel segno del Leone), la sua sezione aurea segnava, diciamo così, il posarsi del Cigno sulle Piramidi e dunque, in modo traslato e simbolico, anche sulla Pertica: cioè, come abbiamo visto sopra, sull’asse polare, che in quel momento aveva raggiunto da non molto tempo Thuban, la nuova stella polare. Un modo di segnare il tempo questo assolutamente sorprendente o addirittura assurdo per i fautori dell’evoluzionismo e del tempo lineare. Al contrario, nulla di più ovvio per chi conosca le profonde “ragioni astronomiche”, e matematico-scientifiche del mito, dove attraverso possenti immagini allegoriche, intrise di scienza sacra, il mutare dei cieli viene rappresentato assieme alla descrizione ermetico-matematica delle forze divine che di tali mutamenti sono la causa.

In uno dei tanti racconti tradizionali citati da de Santillana – strettamente imparentati con quello di Amleto e dunque anche con quello di Osiride – troviamo una storia finlandese, in cui la trama è costruita intorno agli episodi della forgiatura e della conquista di un grande mulino, chiamato Sampo, che non è altro che un modo mitopoietico per alludere all’asse dell’eclittica e a stelle e costellazioni che attorno ad esso ruotano eternamente. Conviene citarlo perché vi troviamo una chiara allusione all’ala del Cigno che va a toccare il cerchio tracciato dal polo terrestre durante la precessione. Una signora chiamata Lohui chiede al fabbro Ilmarinen – un’ipostasi di Saturno che ha il suo parallelo greco in Efesto, e quello egizio nel dio Ptha – di fabbricarlo con questi strani materiali

O fabbro, o Ilmarinen,

grande primordiale artefice,

se saprai foggiarmi un Sampo,

con il suo coperchio variopinto,

dalle punte delle bianche penne d’ala di un cigno,

dal latte di una giovenca sterile,

da un granellino d’orzo, dalla lana di una pecora d’estate,

accetterai poi questa fanciulla

come ricompensa, mia graziosa figliuola?

3.

Questa, come subito si capisce, non è altro che una fin troppo scoperta allusione al cielo intorno al polo dell’eclittica, ovvero alle costellazioni del Nord. In particolare “le punte delle bianche penne d’ala di un cigno” sono proprio quelle stelle del Cigno che fanno parte della sua ala destra, che toccano e oltrepassano il cerchio tracciato dal polo terrestre. E in questo cerchio, che altro non è che il quadrante della meridiana precessionale tanto genialmente imitata dagli architetti di Giza, troviamo l’inizio e la fine di una diversa suddivisione del cerchio della precessione.

Fra l’altro, dal momento in cui attorno al 12100 a.C. Vega era in perfetta corrispondenza con l’asse della Terra, fino al 2465 a.C. – sezione aurea del semiciclo precessionale segnato da Orione al minimo e dall’entrata del Sole nel segno del Leone – sono passati circa 9550 anni. Ma se dividiamo la durata di un intero ciclo precessionale di 26000 anni per il numero di Eulero, uno dei numeri sacri codificati nel lato della Piramide, troviamo che il risultato va vicinissimo a questa cifra, dato che 26000 : 2,718.. = 9564,865..

Dunque, quella correlazione fra il Cigno e le Piramidi, che avviene nella data segnata dai Pozzi Stellari, rappresenta il passaggio da un’Era Divina a un’altra, proprio come accade nell’anno in cui le Piramidi diventano un riflesso terrestre delle stelle della Cintura di Orione, ovvero nel 10500 a.C. E queste due epoche divine – quella che va dal 15.500 al 2500 a.C. e quella che va dal 10500 a.C. circa al 2500 a.C. sono separate dal loro inizio rispettivamente

1) da un periodo di tempo pari a un semiciclo precessionale.

2) da un periodo di tempo pari alla sezione aurea di un semiciclo precessionale.

Invece, il tempo occorso all’asse polare della Terra per passare dall’epoca in cui Vega era la stella polare al 2500 a.C. circa, è stato pari alla durata del ciclo precessionale divisa per il numero di Eulero, vale a dire a circa 26000/e = 9564 anni solari.

Il semiciclo precessionale cominciato, con il termine dell’oscillazione verso il basso di Orione sull’orizzonte di Giza e l’inizio della sua risalita, si concluderà fra due o tre secoli con l’asse terrestre che punta esattamente su Polaris, mentre a Giza Orione, giunto all’apice dell’orizzonte, comincerà il suo percorso di discesa. Da questo momento fino a un nuovo passaggio vicino alla testa del Cigno mancano circa 8050 anni: di nuovo una sezione aurea di un semiciclo precessionale

Dunque, per circa 12100 anni, la Terra resterà senza una vera e propria stella polare. Dividendo la lunghezza dell’intero ciclo precessionale per questi 12100 anni e facendo la radice quadra otteniamo l’altezza della Piramide espressa in metri (146,57) divisa per 10²

√(26000 : 12100) ∙ 10² = √2,148760 ∙ 10² = 1,465865.. ∙ 10² = 146,586.. ≈ 146,57 altezza Grande Piramide

Il paesaggio sacro di Giza si svela dunque infine in tutta chiarezza come una gigantesca meridiana precessionale, costruita per segnare il passaggio da un’Era Divina all’altra, Ere scandite da numeri a loro volta considerati come sacri. Conviene ripercorrere questo complesso intreccio di cicli o “ruote cosmiche” rivedendo in sequenza le immagini con cui lo abbiamo descritto

La regolarità di questi ritmi celesti, e il loro fondarsi su ritmi sacri sembra confermato dal fatto che se uniamo le tre stelle polari e la testa del Cigno, quello che ne viene fuori è a sua volta una figura geometrica regolare.

La figura ricorda il cono della precessione, che a sua volta ricorda quello di una cosmica clessidra. Chissà che non sia proprio questa l’origine di questo antico metodo di misurare il tempo. E sembra anche interessante il fatto che il centro di questa figura, passi per una delle linee che uniscono le stelle del Drago.

Le linee che abbiamo tracciato vanno, per quanto possibile, a cogliere il centro delle stelle. Però avremmo potuto raggiungere un risultato ancora migliore se avessimo utilizzato ogni stella non come un punto, ma come un insieme o un intorno di possibili centri. Un metodo che la quantistica ci ha insegnato per le costanti. A causa del principio di indeterminazione, esse sono più da considerarsi come un punto inesteso su un asse cartesiano, ma come un intorno relativamente indefinito, che sempre di più sfuma verso i suoi confini. Ma visto che l’universo è stato costituito da Dio secondo questi principi, può darsi che essi si applichino, per esempio, anche a un certo tipo di figure regolari che possiamo osservare nel cielo

4.

Questo complesso di ipotesi è ulteriormente rafforzata dalla scoperta fatta da Bauval che fra il 2500 a.C. e il 2080 a.C. (l’epoca del passaggio dalla IV alla V Dinastia) sul paesaggio sacro di Giza si verificarono altri importanti mutamenti celesti. Per comprendere bene di che si tratti, occorre farci un’idea di che cosa sia l’equatore celeste, una cosa che Bauval spiega con chiarezza esemplare

Visto dal nostro pianeta, il cielo appare come un’enorme volta semisferica che copre la terra piatta e apparentemente circolare, posando il bordo più basso sull’orizzonte. Nell’astronomia scientifica, noi dividiamo la parte orientale e occidentale di questa sfera celeste con il meridiano, una linea immaginaria che corre sopra di noi da nord a sud. Noi dividiamo anche la semisfera celeste in una zona meridionale e una settentrionale con una linea immaginaria, l’equatore celeste, tracciata da est a ovest. Questa linea però corre esattamente sopra di noi solo se ci troviamo sull’equatore terrestre; altrimenti, inclina verso sud, attraversando la linea del meridiano a un’altezza di 90°meno la latitudine a cui ci troviamo. Così per chi si trovi nelle vicinanze di Londra, l’equatore taglia il meridiano a un’altezza di 90° – 51° = 39°sopra l’orizzonte meridionale. Per chi si trovi invece nelle vicinanze del Cairo, l’equatore taglia il meridiano a un’altezza di 90° – 30° = 60°sopra l’orizzonte meridionale. L’equatore celeste, quindi, è il «confine» astronomico che separa il cielo superiore da quello inferiore.

(..)

La gigantesca figura celeste di Sahu si estendeva dalle Iadi (la costellazione «meridionale» di Sahu), oltre la costellazione di Orione propriamente detto, fino al Cane maggiore e a Sirio. Come divideva questa «terra» l’equatore celeste?

Servendomi dello Skyglobe 3.5, risalii al 3100 a.C., l’epoca in cui gli egittologi pongono l’unificazione delle Due Terre, proiettando quindi la regione stellare del Duat celeste (Iadi, Orione, e Cane Maggiore) sul meridiano. L’equatore celeste passava poco sopra le Iadi, indicando che queste stelle si trovavano nel cielo inferiore (corrispondente al «Basso Egitto»). Sapendo che l’effetto della precessione provocava uno spostamento verso l’alto delle stelle, decisi di vedere quando le Iadi, e specialmente le due stelle Aldebaran e 311 (Epsilon Taurus), che avevo correlato alle due piramidi di Dashour, avrebbero attraversato l’equatore celeste e si sarebbero spostate nel cielo superiore («Alto Egitto»). Attraversai così i secoli 3100 a.C., 3000 a.C., 2900 a.C. fino al 2000 a.C. Stupefatto, contemplai sullo schermo gli eventi dell’unificazione come erano spiegati nella Teologia menfita. Una vista elettrizzante! Tenendo presente che l’equatore celeste è una declinazione zero e che le declinazioni negative rientrano nel cielo inferiore, mentre quelle positive rientrano nel cielo superiore, limai le date fino all’approssimazione di un decennio. Le letture ottenute sono riportate nella tavola

EPOCA DECLINAZIONE

Aldebaran Stella 311

3100 a.C. -5°35′ -3°29′

2450 a.C. -1°56′ zero

2080 a.C. zero +2°13′

Questi fenomeni precessionali erano quanto mai eloquenti, poiché mostravano che, esattamente all’epoca in cui il re Khufu (Cheope), il supposto costruttore della Grande Piramide, venne al potere, la stella 311 (Epsilon Taurus) era situata in modo da attraversare l’equatore celeste e lasciare il cielo inferiore per quello superiore. Poi, intorno al 2080 a.C. all’epoca in cui i Testi delle piramidi furono iscritti nelle tombe della V e della VI dinastia, lo stesso accadde ad Aldebaran. In correlazione, questo significava che le piramidi di Dashour (Iadi) «appartenevano» all’Alto Egitto in base alla soluzione di una disputa territoriale decisa, non da decreti terrestri, ma dal mistero precessionale delle stelle. Nessun sacerdote avrebbe potuto opporsi alla decisione del consesso degli dèi celesti, la Grande Enneade di Eliopoli.

La base delle prove archeologiche e cronologiche che inducevano gli egittologi a datare l’unificazione delle Due Terre intorno al 3100 a.C. non era quindi confermata dalla precessione ; sembrava perciò che si dovesse pensare a una data più tarda, forse successiva la 2400 a. C, e dunque posteriore anziché anteriore alla IV dinastia.

R. Bauval, A. G. Gilbert, Il Mistero di Orione, TEA, pp. 172-174

5.

Una cosa che Bauval non nota è che i 2°13′ = 2°,2166666.. di declinazione che differenziano l’altezza di Epsilon Taurus da quella di Aldebaran potrebbero avere un significato numerologico di alto interesse, dato che se facciamo la radice ottava della tangente di quest’angolo troviamo quello che sembra un parente molto stretto del Numero della Bestia

⁸√tg 2°216666.. = ⁸√0,038707.. = 0,666000130.. ≈ ⁸√tg 2°,216663197.. ≈ 0,666

Simili strutture matematiche nascoste si trovano sparse ovunque in tutti i miti come nei calendari antichi. Forse, l’unico motivo per cui fino ad oggi non sono state indagate in modo veramente approfondito e soddisfacente è che il pregiudizio della presunta arretratezza dei nostri antenati ci ha finora costretti nell’asfittico sillogismo: antico = primitivo. Un sillogismo diventato col tempo talmente ovvio che oramai non viene più nemmeno formulato, almeno nell’ambito della cultura “ufficiale”. Eppure, se prendiamo la durata di un Grande Anno Maya misurato in giorni (52 ∙ 365 = 18980 giorni), vediamo che anche quello non è altro che una funzione molto ben approssimata di π, oppure di √10. Addirittura, in questo secondo caso, notiamo che la differenza con la funzione esatta corrisponde più o meno alla costante gravitazionale divisa per 10³

18980 : π⁷ = 6,284158.. ≈ 2π = 6,283185..

[18980 : (6 ∙ 10³)]² = 3,163333..² = 10,006677.. (+0,006677.. ≈ G/10³ = 0,006672..

Ma, a parte questo, le osservazioni di Bauval ci confermano nella nostra teoria di fondo, che coincide con quella di de Santillana e von Dechend: ovvero, che nell’antichità profonda dell’umanità, durante quel periodo che noi chiamiamo “Età della Pietra” la storia intesa nel senso occidentale-moderno, iniziata con Erodoto attorno al 500 a.C., non era presa in considerazione, se non come riflesso vago e opaco degli eventi che si verificavano nella volta celeste, intesa a sua volta come un Regno dei Cieli, abitato da divinità il cui simbolo erano stelle, pianeti e costellazioni.

Le stelle fisse sono l’essenza dell’Essere, il loro consesso rappresenta i consigli nascosti e le leggi implicite che governano il Tutto. I Pianeti, visti come dèi, rappresentano le Forze e la Volontà: tutte le forze esistenti, ciascuna vista come un particolare aspetto della potenza celeste, ciascuna un aspetto della spietata necessità e precisione espresse dal cielo. Si potrebbe anche dire che, mentre le stelle fisse rappresentano il potere regale, silenzioso e immobile, i pianeti sono il potere esecutivo.

G. de Santillana – H. von Dechend, Il Mulino di Amleto, Adelphi, p. 184

Gli eventi che narrano, per esempio, le iscrizioni o i papiri Antico Egizi, almeno per quanto riguarda i periodi più antichi, non hanno nulla a che fare con quegli eventi terreni, per così dire, interamente laicizzati, concepiti dall’evoluzionismo a sfondo materialista. Qui troviamo degli esseri umani dapprima in lotta per la l’esistenza con altre specie animali. Poi, una volta che l’uomo afferma la sua superiorità sulle altre specie, la lotta si sposta all’interno della società umana stessa. Il suo oggetto è un potere che non ha nessun rapporto con il sacro: anzi, il sacro è un’illusione generata ad arte per fondare un’autorità che non ha nessun fondamento. Perennemente occupati in queste lotte intestine, gli esseri umani complottano, dichiarano guerre, stringono alleanze con questo o con quello, si rivoltano contro quest’altro e cose del genere. Così educato dai libri e dagli avvenimenti del suo tempo, quando legge un passo di Tacito come quello che citiamo qui sotto, in cui si parla un patrizio romano della decadenza, pronto a qualsiasi crimine e qualsiasi impostura pur di conquistare la corona di imperatore, lo storico occidentale medio non pensa di avere a che fare con una verità legata a un momento storico particolare, ma con una verità metafisica, o, almeno, metastorica

“Nel frattempo Otone, che non aveva nulla da sperare dall’ordine e tutto dal disordine, era spinto da molte ragioni: la sua prodigalità, onerosa anche per un principe, la sua povertà, difficilmente tollerabile anche per un privato cittadino, la sua ira contro Galba e la sua invidia contro Pisone; per rendere poi più acuti i propri desideri, si immaginava inoltre di essere in pericolo.

(..)

I liberti e i servi [di Otone], abituati ad un tenore di vita più corrotto di quanto sia lecito in una casa privata, dimostravano attorno a lui, che ne era avido, che se ne avesse avuto il coraggio, sarebbe stata sua la corte di Nerone, con i suoi adulteri, i suoi matrimoni e quella sfrenata soddisfazione di ogni desiderio, che è caratteristica dei re. Se non avesse osato, altri l’avrebbe avuta.

Tacito, Storie, Libro Primo, 51

6.

Sebbene queste parole siano state scritte diciassette secoli fa, esse corrispondono pienamente alla metafisica evoluzionistica con cui oggi descriviamo tanto il mondo animale come quello umano. Infatti, l’uomo così come viene concepito attualmente, è in lotta per quegli stessi “ideali” per cui lottava Otone: la lussuria e potere, che, con una certa pruderie protestante Freud ha ribattezzato “scientificamente” come istinto sessuale e istinto aggressivo. Altro non si può trovare al mondo che non sia un illusione: se Freud è stato criticato da tutte le parti e in ogni modo, almeno in questo l’evoluzionismo gli ha dato pienamente ragione.

Al contrario di Otone, i Romani dell’alba della Repubblica, che credevano nella Patria, nell’Onore e negli Dèi, ci commuovano per la loro infantile ingenuità. Imbevuti di una fede religiosa che noi consideriamo senza alcuna esitazione come un puro delirio, non si erano resi conto di come vanno “davvero” le cose a questo mondo, di quelli che sono i “veri” interessi degli esseri umani, almeno finché non è arrivata gente come Caligola a spiegarglielo.

Ma a volte il sapere come “davvero” stanno le cose – diciamo così – rende difficile, per non dire impossibile, il già di per sé difficile compito ermeneutico di comprendere dei mondi storici dove quelle che per noi sono illusioni vengono vissute come la piena, perfetta e indiscutibile verità. Lo storico moderno è tanto pronto alla comprensione del vuoto spirituale e delle lotte per il potere in un mondo storico decadente quanto alla più totale incomprensione delle luminose visioni metafisiche di una civiltà al suo sorgere.

Per solito, l’intellettuale occidentale medio vede nella Grecia Classica le origini della sua stessa cultura, che considera nulla di meno che la punta di lancia dell’evoluzione. Questo lo spinge a pensare che della gente tanto intelligente ed evoluta da essere addirittura all’origine dei suoi manuali scolastici, non potesse affatto prendere sul serio delle quisquilie come gli dèi, le feste religiose, la tregua olimpica, gli auspici delle vittime sacrificali e cose del genere. Evoluzione e religione sono da lui pensate come in diretta contraddizione: quanta più religiosità si attribuisce al mondo Greco Classico, quanto più lo si avvicina alle scimmie: e come può essere vicina alle scimmie una cultura sui cui testi si è fondata addirittura la Modernità, quel punto cruciale dell’evoluzione in cui l’uomo prende coscienza infine di non avere una coscienza, e dunque di non essere affatto un uomo, ma solo una scimmia molto complicata?

Quindi, se trecento Spartani vanno a immolarsi alle Termopili assieme al loro re, lo storico occidentale medio non può assolutamente credere che l’avessero fatto per compiere la profezia della Pizia: o un re morirà o l’Ellade sarà distrutta. Bisogna per forza cercare motivi politico-strategici nascosti che, per quanto stupidi o completamente assurdi, lo sono senz’altro di meno che la fede negli oracoli.

7.

Una posizione di questo genere, fondata sul presupposto della più assoluta incredulità verso le motivazioni di tipo spirituale, è perfettamente in linea con la decadenza della fede religiosa che fu all’origine della nostra cultura, vale a dire l’interpretazione gotica del cristianesimo. Una decadenza di cui è facile trovare il corrispettivo nello spegnersi della fede pagana. Alzi la mano chi non trova in questo passo di Burckhardt delle analogie fin troppo scoperte con quel che è successo al cristianesimo a partire da quello che Huizinga ha definito l’autunno del Medio Evo

Alla base del culto sta la generica intenzione di mantenersi benevoli gli Dei, se non altro con il timore; il loro antico aspetto era stato assai pauroso, ed è ancor vero il motto di un romano « Primus in orbe deos fecit timor » (Petronio). E nello stesso tardo periodo, in cui la bellezza delle figure divine e dei miti non aveva più il potere di affascinare e confortare gli uomini, sorge anche quell’opera di Plutarco da cui risulta che il timore era l’unica cosa che restasse ancor viva nella maggior parte della gente. La filosofia nel frattempo si era pronunciata positivamente con la trasfigurazione del concetto di Dio, negativamente con l’ateismo e con la dottrina epicurea dell’indifferenza degli dèi; e per il popolo era come se non fosse mai esistita.

Jacob Burckhardt, Storia della Civiltà Greca, Volume I, Sansoni, 1955, p. 568

Quel che è accaduto in Grecia a partire dalla Guerra del Peloponneso è cominciato ad accadere, sia pure in forma diversa, all’interpretazione gotica del cristianesimo a partire dalla Riforma. Da quel momento in poi si assiste alla perdita di fede da parte della gerarchie ecclesiastiche, che cominciano a temere per il loro potere e il loro prestigio. Il cielo vuoto delle tragedie di Shakespeare, l’etica cavalleresca che diventa il trastullo di Cervantes, sono lo specchio del Pascal che – ripetendo inconsapevolmente « Primus in orbe deos fecit timor » – inaugura un filone particolarmente odioso di quella che assumerà nei secoli il nome altisonante di “teologia negativa”. Dio non è più un’entità luminosa in cui misticamente ci si perde, ma un “Deus absconditus”, un’entità oscura in cui si crede solo per evitare una minaccia infinita. La tanto celebrata “scommessa pascaliana” è il trionfo di un monstrum che possiamo definire “utilitarismo religioso”. L’uomo scommette la sua vita terrena per quella eterna in base a un calcolo economico che più piccolo borghese non si può. La vita terrena non è altro che un susseguirsi di miserie. Tanto vale allora rinunciare ai piaceri (quali?) credere in Dio (il che vuol dire sostanzialmente: attenersi al culto e alla morale) e vedere quel che succede dopo. Se c’è Dio abbiamo vinto, sennò svaniamo nel nulla, e anche questa in fondo è una forma di paradiso. Cosa potesse pensare un San Bernardo di una “vita spirituale” (!?) di questo genere è fin troppo facile immaginarlo.

Nel contesto di una decadenza tanto avanzata, la reazione della gerarchia è stata inevitabile: brrr…, se l’incredulità si diffonde in questo modo, su quali basi saremo capaci di giustificare potere e ricchezze? Come vivere più a caviale e champagne alle spalle del popolo, se un bel giorno il popolo comincia a fregarsene di Dio ancora di più di quanto ce ne freghiamo noi? Quando Voltaire ha scritto “Se Dio non ci fosse bisognerebbe inventarlo”, non ha inventato nulla: non ha fatto altro che sintetizzare laicamente i dettami della “teologia” cattolica, cresciuta a partire da Riforma e Controriforma. Alla fine, il possente edificio spirituale del Medio Evo si è immiserito fino al punto di trasformarsi in una morale sessuale che è diventata sempre più fanatica e beghina via via che la Chiesa perdeva il potere repressivo garantito dal possesso di una forza militare adeguata allo scopo. C’è chi ha visto nelle discussioni sul sesso degli angeli un sintomo di decadenza incipiente: che dire allora di quella maniacale “perscrutatio mutandarum” che vede incombenti occasioni di peccato mortale anche nelle operazioni più elementari di igiene intima? Ci si domanda come mai i “poètes maudits” si siano dati tanto da fare per cercare la loro dannazione, quando era tanto facile trovarsene una semplicemente stando seduti sul bidet.

D’altra parte, il rimedio è la logica conseguenza del danno e ne porta le stimmate. Visto che la guardia svizzera non può terrorizzare nessuno, il senso di colpa era diventato l’unico strumento di coercizione possibile per garantirsi il potere sulle menti e sui corpi dei fedeli. L’uso che le varie confessioni ne hanno fatto è stato talmente largo e smodato da identificarsi infine con la fede tout court. Il giorno che Freud arriverà a teorizzare che la religione non è altro che uno strumento per la repressione degli istinti sessuali, non farà altro che mettere in chiaro e per iscritto quello che oramai da un paio di secoli ne pensavano in modo più o meno oscuro le gerarchie vaticane e i pastori protestanti.

8.

Ciò fa sì che anche guardando agli albori della nostra stessa cultura lo storico odierno si trovi in uno stato di grave difficoltà. Oggi, come negli ultimi due o tre secoli la fede, non è altro che un pretesto per lotte di potere: dunque, come è possibile che sia mai stata altro? Davvero c’è stata al mondo della gente che prendeva per buone quelle bubbole? Perfino i ricordi del liceo diventano enigmatici: come è possibile che per un uomo come Dante l’amore per Beatrice fosse qualcosa di diverso da un pretesto estetico per scrivere i suoi pur splendidi sonetti? Come è possibile che le cattedrali siano state qualcosa di più che il simbolo della supremazia culturale e del potere politico e militare che una casta sacerdotale cinica e istruita esercitava spietatamente sul popolo bue?

Lo storico occidentale moderno medio, ma spesso anche l’intellettuale cattolico, cadono nella più profonda perplessità, e forse addirittura si tormentano. Dio si fa Uomo, muore sulla Croce, e dopo tre giorni risorge: per quale altro motivo può essere accaduta un’enormità del genere? Non c’è altra risposta: deve essere stato per impedire che i comunisti mettano l’Imu sugli istituti religiosi.

Riconosciamo infine di trovarci in una quasi perfetta condizione di oscurità: le “spiegazioni” dell’origine della religione, col passare del tempo e l’accumularsi dei volumi diventano ancora più cervellotiche e oscure dei fenomeni che dovrebbero interpretare. Si arriva al punto che in un certo genere di teorie l’oggetto della teoria scompare del tutto, e al suo posto si parla di cose toto genere diverse. D’altra parte, perché stupirsi? Dio e la contemplazione di Dio sono la stessa cosa e svaniscono l’uno insieme all’altro: il passaggio dalla fede contemplativa al pragmatismo clericale lo si può registrare anche nelle storie del Graal. Dunque, le cause che un economista come Marx trova del fenomeno religioso sono in tono – oltre che con la piega che ha preso il cristianesimo occidentale – anche con il nichilismo, che già ai suoi tempi ha preso piede fino al punto di diventare una sorta di non dichiarata fede laica. Una strana ateologia con cui oggi siamo portati a renderci ragione del mondo e della storia rifiutando di attribuirgli una ragione di qualsiasi genere.

Analizzare e neutralizzare questo sistema di pregiudizi con cui noi guardiamo a un mondo come quello Antico Egizio è il compito delle due parti successive di questo lavoro. Nell’ultima tireremo le fila del ragionamento che abbiamo svolto, per avere un’idea complessiva del senso che il Plateau di Giza e il paesaggio stellare che da lì si può ammirare possono aver avuto per i suoi costruttori.

Capitolo 13:

PROBLEMATICHE CONNESSE ALL’INTERPRETAZIONE DELLA RELIGIONE ASTRONOMICA PALEOLITICA E POST PALEOLITICA

1.

In effetti, se pensiamo a quello strano modo di calcolare il tempo che abbiamo visto fino ad adesso, interpolando cicli cosmici che come minimo superano il millennio – quali quello di Sirio, o quello dell’allineamento fra Saturno, Venere e Mercurio – non troviamo proprio nulla di familiare. Di fatto, tutto questo cervellotico e ossessivo calcolare, sembra ad un Occidentale moderno non solo e non tanto inutile, non solo e non tanto follemente complicato, ma prima e ancor di più completamente assurdo. A cosa diavolo può servire di fissare la data del solstizio d’inverno del 2012 a partire da un anno vago – come fecero i Maya – quando poi la loro cultura si è estinta un millennio prima di quella data? Non avrebbero fatto meglio a pensare al presente e ai bisogni impellenti della sopravvivenza, invece di perdere tempo a contare i giorni di un’eternità che non si sa che cosa sia o non sia, se esiste o non esiste?

Non c’è nulla da fare. Se disperdevano le loro energie in occupazioni tanto insensate, questo significa che i Maya erano comunque sia dei bruti, a dispetto della loro abilità tanto nei calcoli astronomici che architettonici. In effetti, da questo punto di vista, questa gente assomigliavano più ai diavoli della loro religione che a esseri umani. La loro precisione è arrivata al punto che nel giorno dell’equinozio il corpo di luce di un serpente si disegna sulle scalinate sulla più celebre delle loro piramidi, quella di Chichen Itza, andando a congiungersi con le fauci spalancate che lo attende monca per tutto il resto dell’anno

Uno spettacolo grandioso, non c’è nulla da dire. Eppure erano ugualmente dei bruti, della gente arretrata, perché se non lo fossero stati si sarebbero resi conto dell’ovvia e universale finitezza di tutto e del Tutto, che, alla fine, è il solo vero significato del tempo cosmico. Non avrebbero dilapidato i pochi giorni della minuscola vita umana in imprese tanto smisuratamente inutili, e avrebbero pensato a godersela un po’ di più (come tentò di fare il buon vecchio Otone, ci viene spontaneo aggiungere).

Questo è il nostro punto di vista sul mondo antico, conscio o inconscio che sia. Eppure questo punto di vista, come il giudizio di valore che ne risulta, non è affatto, come si potrebbe anche credere, un giudizio oggettivo, che risulta da criteri scientifico-quantitativi non ulteriormente questionabili. É, molto semplicemente, una conseguenza del fatto che noi di solito operiamo con i numeri per degli scopi totalmente diversi che costruire delle immagini matematiche internamente simmetriche e quasi musicalmente armoniche di cicli cosmici come quelli di cui ci si occupava nell’antichità. La loro durata ci pare abissale, facciamo fatica anche solo cercare di capire che senso possa avere immaginarla, e il loro esistere o meno ci lascia perciò in una totale indifferenza. Siamo troppo occupati a pensare o a fingere di pensare al presente, per avere tempo di pensare al Tempo.

Ma una tale indifferenza, a sua volta, non è la conseguenza di un’obbiettività di tipo scientifico, ma delle nostre inclinazioni spirituali. Il fatto è che nell’Occidente moderno si considera la vita umana come un intervallo fra due eternità di nulla. Così, a noi persino i due minuti di tempo che un computer ci mette a entrare in funzione ci possono sembrare – appunto – un’eternità di nulla.

Ma quando ci volgiamo allo studio di culture che hanno delle radici e una visione del mondo tanto diverse e lontane dalle nostre occorre tenere a mente che abbiamo a che fare con uomini che pensavano a sé stessi e al mondo che li circondava in modo radicalmente opposto. Ma questo non accadeva certo perché fossero più vicini alla condizione animale, come vuole il nostro pregiudizio. Al contrario, come ci pare di aver abbondantemente dimostrato nel corso di questo lavoro, essi possedevano una matematica e una scienza molto più avanzate delle nostre. Il che significa a sua volta che la religione, in sé e per sé non è affatto nemica della scienza e della matematica, se non nelle degenerazioni di cui abbiamo avuto testimonianza negli ultimi due millenni, e in particolare negli ultimi quattro o cinque secoli.

Quei teologi cattolici che hanno fatto di tutto per ostacolare i progressi della scienza non hanno fatto altro che ostacolare i progressi della fede, dato che tutto il lavoro che abbiamo finora svolto è la dimostrazione che a fondamento della struttura matematica dell’universo vi è la Mente Divina, e non il caos. Ed è solo perché si era capito questo che nell’antichità non ci si occupava della storia comune, ma del mito: perché nel mito, cioè nei mutamenti del cielo, essi potevano contemplare l’essenza di quella legge segreta con cui la Mente Divina lo ha formato. Infine, perché occuparsi di questa o quella battaglia, del carattere e della biografia di quel condottiero o di quell’imperatore, se contemplare il cielo è contemplare la mente di Dio nel mentre opera, se i suoi mutamenti non sono altro che l’Eternità che nel farsi Tempo si fa Musica, se contemplare le stelle è come guardare Dio negli occhi?

2.

Nel loro classico saggio sul mito e sulla struttura del tempo de Santillana e von Dechend notano – soffermandosi sul poema più celebre del poeta iranico Firdusi – che

“la «storia» incomincia solamente quando l’Impero persiano scompare dalla scena e subentrano i successori di Alessandro. Togliere dalla storia le grandi e solidamente storiche imprese di Dario I, di Serse, di Cambise, ecc., è paradossale per un poema il cui scopo è celebrare l’Impero persiano. È presumibile che Firdusi intendesse che, fino a quando regnò la religione zoroastriana, il tempo fu sacro e quindi appartenente al mito piuttosto che alla storia comune.

(..)

Ma qui ci viene finalmente data apertis verbis una chiave per penetrare nel significato delle immagini, cioè le parole culminanti di Khusraw (Khusraw è l’eroe protagonista del poema di Firdusi)

Il mondo intero è il mio reame, tutto è mio

dai Pesci giù fino alla testa di Toro.

Se un eroe dell’emisfero occidentale proclamasse: «Tutto questo continente è mio da Hatteras a Eastport» (il capo Hatteras è nella Carolina del Nord, Eastport è sulla costa del Maine al confine tra Stati Uniti e Canada) lo si riterrebbe affetto da mania unidimensionale: forse nella sua mente quel tratto di costa simboleggia un intero continente? Qui però le parole hanno perfettamente senso perché Kay Khusraw non si riferisce alla terra, bensì a quella sezione dello zodiaco compresa tra i Pesci e Aldebaran, i trenta gradi che abbracciano la costellazione dell’Ariete. Ciò significa che il suo regno non è solamente dei cieli, è essenzialmente un regno del Tempo. Il Tempo è la dimensione del cielo. Kay Khusraw si presenta come una funzione del Tempo preordinata da eventi dello zodiaco.

(de Santillana von Dechend, Il Mulino di Amleto, Adelphi, p.113 e p. 70).

Che il tempo sia sacro, in culture appassionate di cicli cosmici, significa che viene considerato un ciclo di eterno ritorno di dèi stellari, o solari, lunari, o planetari. È ovvio che in un contesto di questo genere le vicende e le figure “reali” di esseri umani da noi ritenuti anche molto importanti, compresi Dario I, Serse e Cambise, diventano al contrario piuttosto irreali. Oppure, quando i loro nomi vengano ricordati, tendono rapidamente a confondersi con gli dèi e gli eroi del mito (una cosa del genere è successa proprio ad Alessandro Magno, la cui figura, dopo la sua morte, venne ben presto confusa, se non proprio identificata, con quella di Dioniso conquistatore dell’Asia). Allo stesso modo le vicende reali di una battaglia come quella di Qadesh, nella stele di Ramses diventano il pretesto per celebrare la potenza e la benevolenza di Horus verso l’Egitto. Gli Antichi Egizi non si interessavano di fissare un concatenarsi di accidenti più o meno casuali – l’intelligenza tattica o strategica di un generale, una nuova arma, il numero dei soldati, il tempo atmosferico, etc.

Lo stesso vale per eventi come il Diluvio o i Diluvi di cui si parla in migliaia di miti sparsi in tutto il mondo. Noi, interessati esclusivamente dagli eventi che riguardano direttamente la nostra vita, interpretiamo queste storie in modo letterale. Questo perché

Oggi, gli uomini vengono addestrati a pensare in termini spaziali, a localizzare gli oggetti. Dopo l’infanzia la prima domanda è: «Dove e quando è accaduto?». A mano a mano che la scienza e la storia invadono l’intero campo del pensiero, gli eventi del mito retrocedono a pura favola e ci appaiono come fantasie d’evasione: mancano di collocazione e di serietà; il loro spazio è ubiquo, il loro tempo è circolare.

G. de Santillana – H. von Dechend, Il Mulino di Amleto, Adelphi, p. 73

Ciò fa sì che per uno storico moderno è intollerabile il pensiero che al mito non corrisponda qualcosa nella “realtà”. Il fuoco che nella tradizione coopta scende dal cielo a incendiare le città degli uomini, lo vediamo come la proiezione mitica di eruzioni vulcaniche catastrofiche, o di meteoriti gigantesche, o di esplosioni solari etc. Nell’acqua che tutto sommerge vediamo le alluvioni, i maremoti e gli tsunami giganteschi che, a quanto pare, hanno effettivamente devastato la terra verso la fine dell’Era Glaciale, attorno al 13.000-10.000 a.C.

Ma questa nostra interpretazione trascura il fatto che in quelle epoche gli esseri umani vedevano questi avvenimenti come l’epifenomeno dei mutamenti che si verificavano all’orizzonte in momenti topici del ciclo solare, non come fenomeni autonomi, dotati di una sostanza vera e propria.

In particolare, la costellazione o “casa dello zodiaco” su cui il Sole si va a posare al tramonto dell’equinozio d’autunno, nel momento del transito alla costellazione successiva, viene dapprima “incenerita” dalla luce solare (il fuoco che viene dal cielo): questo accade perché la costellazione, al momento del tramonto, rimane troppo bassa all’orizzonte, cioè troppo prossima al Sole, che col passare del tempo, siccome tende a rendere invisibile la debole luce delle stelle, simbolicamente “le incenerisce”. Ma siccome ogni configurazione celeste corrispondente ad ogni segno zodiacale è un mondo (fra qualche riga de Santillana e von Dechend ci spiegheranno di che “mondo” si tratta) ecco che “il fuoco viene a bruciare la terra”.

Dopo questa prima fase di “fuoco” la costellazione, scendendo sempre più in basso, “annega” infine in delle “acque” che altro non sono che quelle del “mare” che si trova oltre la “terra” costituita dal piano dell’eclittica, la cui direzione e i cui confini sono tracciati dal e nel cerchio dello zodiaco. Invece, la costellazione che sorgeva all’alba dell’equinozio di primavera, si solleva sempre più in alto fino a che “ascende al cielo senza conoscere la morte“: come, per esempio, Elia, Enoc, Kay Khusraw, Yudhisthira, Quetzalcoatl

Lungo la fascia zodiacale vi sono quattro punti essenziali che dominano le quattro stagioni dell’anno: nella liturgia della chiesa essi sono appunto i “quattuor tempora” contraddistinti da astinenze particolari, e corrispondono ai due solstizi e ai due equinozi. Il solstizio è l’inversione di marcia del Sole al punto più basso dell’inverno e al punto più alto dell’estate. I due equinozi, quello di primavera e quello d’autunno, essendo i due punti di intersezione dell’equatore con l’eclittica, dividono l’anno a metà, con un uguale opporsi della notte al giorno. Questi quattro punti presi insieme costituivano i quattro pilastri o angoli di quella che veniva chiamata la «terra quadrangolare».

Questo è un elemento essenziale che merita maggiore attenzione. Si è detto poc’anzi che «terra» è il piano ideale passante per l’eclittica; possiamo intanto migliorare la definizione: «terra» è il piano ideale passante per i quattro punti dell’anno, gli equinozi e i solstizi. Dal momento che le quattro costellazioni sorgenti eliacalmente ai due solstizi e ai due equinozi determinano e definiscono una «terra», questa viene detta quadrangolare (e nient’affatto creduta tale dai cinesi “primitivi”, ecc.). E dal momento che le costellazioni dominano i quattro angoli della terra quadrangolare solo temporaneamente, si può legittimamente parlare della fine di una simile terra, e della nascita dalle acque di una terra nuova, con quattro costellazioni nuove sorgenti ai quattro punti dell’anno.

(…)

Era questa la porzione di superficie terrestre conosciuta nella tarda antichità e che dai Greci veniva chiamata , “ecumene”: la terra abitata. È comprensibile che i Greci indicassero con il nome di  la fascia dello zodiaco, delimitata dai tropici, che aveva sì un’ampiezza latitudinale, ma che purtuttavia abbracciava l’intero cielo ed era «abitata» dagli attori che contavano, ossia dai pianeti.

G. de Santillana – H. von Dechend, Il Mulino di Amleto, Adelphi, p. 90

Possiamo farci un’idea piuttosto chiara della conformazione di cosa sia questa che tanto a lungo è stata classificata come l’ingenua e al tempo stesso enigmatica Flat Earth Theory osservando l’immagine che vediamo qui sotto

Che gli spazi cosmici sopra e sotto l’eclittica fossero considerati delle “acque”, e che il piano dell’eclittica fosse considerato la “superficie del mare” (che dunque, in realtà, è un mare sopra o sotto la cui superficie vi è in ogni caso un altro abisso) ce lo conferma non solo il racconto biblico della creazione. Nel Genesi “la superficie del mare” che “separa le acque che sono sopra il firmamento da quelle che sono sotto il firmamento” non è altro che il piano dell’eclittica al di là della “terra”, e la “terra” altro non è che lo spazio cosmico simbolicamente inteso come il cerchio ideale che lo zodiaco traccia attorno a un osservatore che si trovi sul nostro pianeta.

Questo ce lo confermano anche le innumerevoli rappresentazioni Antico Egizie in cui gli astri sono rappresentati come esseri umani o animali che vanno su delle barche. E ce lo confermano anche le immagini che troviamo nelle grotte paleolitiche, dove corpi celesti e costellazioni sono rappresentati come animali che, appunto, galleggiano come su un liquido. In entrambi i casi gli esempi che potremmo portare sono talmente tanti che forse è bene fermarci a queste due immagini che vediamo qui sotto. Il lettore potrà trovarne decine di altri esempi con un rapido giro su internet.

La prima delle immagini che mostriamo è tratta dallo Zodiaco di Senmut. La seconda è una stele di Gobekli Tepe in cui un animale che sembra una pecora, invece di camminare su un prato, disegna un surreale semicerchio all’orizzonte.

3.

Che la “terra” galleggi sulla superficie di un “mare” i cui ubicui abissi si trovano in alto come in basso, come nelle quattro direzioni dello spazio, significa ovviamente che i diluvi di cui si parla nei miti sono eventi astronomici e niente altro. Con ogni probabilità, in molti casi rappresentano il passaggio da un’era zodiacale a un’altra. A volte, come a Giza, sembrano avere a che fare con il ciclo di Orione all’orizzonte, e dunque si verificano solo una volta per ogni ciclo precessionale. Altre volte, sembrano aver a che fare con il passaggio da un stella polare all’altra

Secondo i Mongoli, la Stella Polare è un «pilastro dalla cui stabilità dipende la giusta rotazione del mondo, oppure una pietra che chiude un’apertura: se la pietra viene tolta, l’acqua fuoriesce dall’apertura per sommergere la terra».

G. de Santillana – H. von Dechend, Il Mulino di Amleto, Adelphi, p. 260

E questa interpretazione del mito ha, fra i molti meriti, anche quello di renderci pienamente comprensibile quel passo del Timeo in cui Platone dice che gli Egizi conservavano la memoria di molti Diluvi, e non solo di uno, come i Greci e gli altri popoli (questo Diluvio, di cui anche i Greci conservavano la memoria, Platone lo colloca circa 9000 anni prima del suo tempo: una data abbastanza vicina dunque al 10500 AC). Seguendo il pensiero di de Santillana e von Dechend, quella frase non vuol dire che gli Antichi Egizi erano sopravvissuti e conservavano la memoria di molte inondazioni del globo terrestre. Significa invece che hanno conservato la memoria di numerose volte in cui un ciclo o un semiciclo precessionale è giunto alla fine per iniziare di nuovo .

Le sfingi leonine con due teste che guardano in direzione opposta alludono proprio a questo fatto. Che ogni volta che il Sole entra nel segno del Leone, quando a Giza Orione raggiunge il punto più basso, un ciclo precessionale finisce e uno ricomincia. Per questo le sfingi hanno quasi sempre delle teste leonine, per questo quasi sempre sono messe in coppie, che molto spesso guardano in due direzioni opposte. Insieme rappresentano non più il tempo, ma l’eternità rappresa nel cerchio. E non è affatto privo di interesse il fatto che rappresentazioni di questo genere si possono trovare anche nella cultura Maya, anche se in questo caso abbiamo dei puma, e non dei leoni. Questa è l’ennesima testimonianza dell’intimo, ancestrale legame, fra il Sudamerica Precolombiano e Mediterraneo Orientale preistorico, dove l’eterno ritorno dei cicli cosmici è stato espresso anche per mezzo di simboli che, pur conservando la medesima struttura delle sfingi egizi, usavano come simbolo altri animali

I due leoni dell’immagine che vediamo nella prima fila a destra rappresentano al tempo stesso l’inizio e la fine di quell’Anno Divino, che a Giza si misurava con l’entrata del Sole nel Leone alla levata eliacale dell’equinozio di primavera (questo è anche il senso dei leoni troviamo sulla stele della Sfinge nella seconda fila a destra). Una guarda verso la morte, cioè verso l’Anno Divino che è trascorso. L’altra guarda in direzione della vita, cioè di quello che comincia. Ma siccome il tempo divino si muove in uno Stesso, Eterno Cerchio, è come se i Leoni si guardassero negli occhi.

La croce la vediamo appesa a un geroglifico, che altro non è che un’immagine del Sole equinoziale. Molti millenni prima, troviamo qualcosa di molto simile nella grotta di Cosquer. Quel semicerchio che vediamo al centro è il Sole all’alba dell’equinozio. Le due strisce che si dipartono dall’osservatore ideale, puntano invece ai due opposti solstizi

4.

In questo caso, la Croce Egizia sembra rappresentare l’asse dell’eclittica, attorno a cui il cerchio divino si avvita eternamente. Questo simbolo ha probabilmente vari significati. Quella sorta di cappio, che gestalticamente può essere visto come una testa, può essere visto anche come un simbolo dell’utero, ovvero dell’origine della vita. Un simbolo che, come vedremo fra poco, è profondamente connesso con la religione astronomica del Paleolitico. Oppure, per venire a un tempo a noi più vicino, può sembrare, come il S. Michele che vediamo qui sotto, una figura umana con le braccia aperte

L’immagine che vediamo qui sotto è ancora più pregnante e significativa, e, a suo modo, anche esplicita. Vi vediamo una barca che sembra sorretta e trascinata da onde che, in realtà, sono le spire di un serpente. Questa strana creatura, nel mentre gli consente di galleggiare e di muoversi (le spire del serpente sembrano qualcosa come una corrente) al tempo stesso minaccia i naviganti, uno dei quali è senz’altro il Falco Solare Osiride-Horus. L’altra figura dovrebbe essere Seth, che, in questo caso, sembra comportarsi come un alleato di colui che in altri contesti appare come un suo nemico. Seth infatti sembra difendere il dio Sole da questo serpente, che sembra volgersi minaccioso

Anche in questo caso abbiamo a che fare con una rappresentazione mitica del ciclo precessionale, e dunque della “navigazione” del Sole attraverso i segni zodiacali. Questo viaggio viene simbolicamente consentito dal ruotare delle sfere cosmiche, che è mosso da quel motore immobile che è l’asse dell’eclittica, attorno al quale si avvita eternamente quella che oggi viene chiamata la costellazione del Drago. Ma il Drago ha preso molte forme nel corso dei millenni. Ad Altamira e a Chauvet ha preso la forma di un bufalo, ma non è da escludere che la sua forma possa esser stata interpretata anche in un altro modo. A volte quello che per noi assume la figura di un drago, ha preso la forma di un serpente, magari cornuto e alato: perché nella cultura ermetica Antico Egizia non potrebbe aver preso le forme di un serpente tout court?

In effetti, è cosa arcinota che gli Antichi Egizi – proprio come accadeva nel Sudamerica Precolombiano o come accade ancora oggi in Estremo Oriente – consideravano sacri i serpenti velenosi. Vi era addirittura la credenza che chi morisse per mezzo del morso di un serpente diventasse immortale. A livello simbolico il ragionamento è perfetto: se le divinità dell’orizzonte nascono e muoiono a causa dell’eterno avvitarsi del Serpente Celeste attorno al polo dell’eclittica, morire a causa del morso di un suo avatar terrestre significa essere destinati a un’eterna rinascita. In questo senso, possiamo dire che la visione astronomica che de Santillana e von Dechend danno dell’Okeanos di cui Socrate parla nel Fedone non si contrappone affatto a quella “biologista” che Onians offre nelle Origini del Pensiero Europeo, dove

“Okeanos vi viene paragonato all’Acheloo, il fiume primordiale che «era rappresentato come un serpente con corna e testa umana». Il testo prosegue

«L’elemento procreativo del corpo era l che si manifestava in forma di serpente. È oramai chiaro che era la delle origini, concepito come un serpente, connesso al liquido della procreazione..”

G. de Santillana – H. von Dechend, Il Mulino di Amleto, Adelphi

A questa visione, che de Santillana e von Dechend citano come esempio di, diciamo così, “riduzionismo antiastronomico” della moderna ermeneutica del mito, gli autori de Il Mulino di Amleto parlano di un Okeanos che non è altro che la trasfigurazione delle «Acque Superne»

“L’Okeanos del mito conserva queste maestose caratteristiche di lontananza e di silenzio; era l’unico che poteva restarsene per conto proprio quando Zeus imponeva la presenza nell’Olimpo di tutti gli dèi. Fu lui a mandare le proprie figlie a piangere su Promèteo proscritto e incatenato, lui a offrire la propria possente mediazione in suo favore. Egli è il Padre dei Fiumi; anzi, appare nebulosamente come l’originario dio del cielo di un lontano passato. In un inno orfico viene presentato come «diletto limite della terra, signore del Polo», e in quella famosa opera lessicografica dell’antichità che è l’Etymologicum Magnum il suo nome viene fatto derivare da «cielo».

G. de Santillana – H. von Dechend, Il Mulino di Amleto, Adelphi, p. 230

A uno sguardo distaccato queste due visioni non sembrano affatto contrapposte. Anzi, esse paiono completarsi a vicenda. Nell’ambito del pensiero mitopoietico, le spire del Serpente Celeste possono essere paragonate a un fiume, che non è altro che il fiume del Tempo. Il Fiume del Tempo può diventare Padre di tutti i Fiumi, e dissolversi poeticamente in quelle Acque Superne in cui è destinato a nuotare per l’eternità. Qui non abbiamo a che fare con un pensiero analitico, che procede per distinzioni. Qui abbiamo a che fare con un pensiero simbolico, che procede per concrezioni: l’uccello può essere il simbolo dell’aria o del vento, il vento o l’aria quello dell’uccello; la fiamma può essere simbolo del calore, il calore può essere il simbolo della fiamma; Cristo, il cui simbolo diventerà il Pesce, sceglie i suoi Apostoli fra i pescatori, li fa tornare in acqua per una pesca miracolosa, moltiplica pani e pesci, cammina sulla superficie del lago in tempesta, parla alle folle da una barca, trasforma Pietro in un pescatore di uomini. Ognuno di questi simboli rimanda all’altro, proprio come il nome del Re Pescatore rimanda al lago su cui è costruito il suo castello.

Così, che il serpente serva per simbolizzare il fluido vitale non contraddice le potenzialità mortali del suo morso. In questo senso, non pare un caso che molto spesso la fine di un’era cosmica sia accompagnata dall’apparire di serpenti. Quetzalcoatl salpa su una zattera fatta di serpenti annunciando che un giorno sarebbe ritornato a giudicare i vivi e i morti. Oppure, se andiamo a vedere un racconto relativamente recente, quello che Livio fa delle vicende di Lucio Giunio Bruto (un parente stretto di Amleto, e dunque anche di Osiride, Krishna, etc.), la fine del regno di Tarquinio – un re che, lo sottolineiamo, appartiene al mito e non alla storia – viene preannunciata da un evento miracoloso e orribile

Mentre [Tarquinio] si occupava di ciò [alcune opere difensive]apparve un orrendo portento: un serpente, scivolato fuori da un colonna di legno, fu causa di terrore e di fuggi fuggi nela reggia; ma il re non fu tanto colto in cuor suo da improvvisa paura, quanto da angosciose preoccupazioni.

G. de Santillana – H. von Dechend, Il Mulino di Amleto, Adelphi, p. 42

Sembra tutto meno che un caso il fatto che il serpente scivoli via da una colonna di legno, dato che l’asse dell’eclittica è stato altrettanto spesso rappresentato come una colonna che come un albero. E una colonna di legno, infine, è anche un’allusione a un albero, come un albero può essere inteso come una colonna di legno: proprio in questo modo si è arrivati infine a concepire la Croce di Cristo. Anche in un libro di derivazione almeno parzialmente Antico Egizia, quale il Pentateuco, troviamo che sull’Albero della conoscenza sta un serpente tentatore. E il Drago, o Serpente, si muove proprio in quella zona del cielo, dove gli assi portanti dei cicli cosmici terrestri fanno fulcro

Se adesso andiamo a vedere una delle immagini citate da de Santillana e von Dechend ne “Il Mulino di Amleto”, troviamo che nello strano “tiro della fune” che alimenta la “Possente Frullatura dell’Oceano di Latte” la parte della fune la fa proprio un gigantesco serpente. Ma siccome la Possente Frullatura dell’Oceano di Latte non è altro che un’espressione mitopoietica, che si riferisce al millenario ruotare del cielo stellato attorno all’asse dell’eclittica, i dubbi che restano quanto all’identità del serpente in questione sono infine assai pochi. E a conclusioni simili ci spinge l’analisi della stele di Horus e Seth che “uniscono le Due Terre”. A unire le Due Terre, come abbiamo visto sopra, non è un re con una guerra, ma il movimento ascendente del cielo dovuto alla precessione. E Horus e Seth, nell’immagine sottostante, sono impegnati a manovrare uno strumento che assomiglia in modo fin troppo caratteristico a quello dell’immagine indiana, che si riferisce al Mahabharata. A questo punto della nostra analisi, nessuno forse si sentirà di ipotizzare che sia un caso, che il totale delle tacche in cui lo strano strumento che Horus e Seth stanno manovrando fa proprio 70, cioè “trois-vingt-dix”, “tre-venti-dieci”. Di queste 70 tacche, 36 – cioè la metà di 72 e un decimo di 360 – sono nella parte superiore dell’asta; se alle 34 della parte inferiore aggiungiamo quelle 2 che sono nascoste e/o simbolizzate dalle corde, arriviamo a 72. Questa sembra una suddivisione particolare del ciclo precessionale. Invece che in 360 periodi di 72,222.. anni solari ciascuno, in 72 periodi di 361,111.. anni solari ciascuno. Possiamo ottenere ancora una volta questa cifra dividendo 70 – cioè “trois-vingt-dix” – per 60 – cioè “trois-vingt”. Se poi sottraiamo 1 e moltiplichiamo per 10³ il numero che otteniamo è proprio quello

5.

Dunque, il segno dello zodiaco su cui il Sole sorge all’equinozio di primavera non identifica solo una certa era: identifica anche il Sole, lo battezza, dato che col mutare della sua “casa” muta anche la sua identità. Quel serpente che ruotando attorno all’asse del cielo stellato lo ha fatto nascere e lo fa navigare, al tempo stesso crea nuove epoche e, come dicevano i Maya, da inizio a Nuovi Soli. Nuovi Soli, ognuno dei quali però rappresenta la morte di quello vecchio, come possiamo capire a partire dall’immagine Antico Egizia che abbiamo visto sopra. Il serpente-fiume, dalle cui spire vengono trasportati, continuamente li trascina in un ciclo infinito di morti e rinascite, che sono poi la spiegazione di quelle “tombe degli dèi” su cui Frazer ironizza ne Il Ramo d’Oro, perché da buon occidentale moderno non riesce a concepire degli dèi che nascono e muoiono per l’eternità. Se un dio è un dio, secondo lui, non può né nascere né morire.

Invece questa è una cosa che risulta infine del tutto ovvia, quando comprendiamo che il fondamento delle religioni ancestrali non era una concezione metafisica completamente astratta, quale quella di un Tommaso d’Aquino. Al contrario, si trattava di una visione saldamente e concretamente correlata ai cicli eterni del cielo, in cui “nuovi cieli e terre nuove” sono destinati a nascere e a perire continuamente. A ben pensare, quale altro può essere il fondamento della metempsicosi, se non l’identificazione del destino dell’uomo con quello delle stelle?

Ed ogni morte consiste, all’equinozio di autunno, in un “affondamento” della costellazione che era “in carica” sotto la “superficie” dell’eclittica.

Nelle rozze e vivide immagini delle popolazioni scandinave Amlodhi si distingueva per il possesso di un mulino favoloso dalla cui macina ai suoi tempi uscivano pace e abbondanza. Più tardi, in tempi di decadenza, il mulino macinò sale; ora infine, essendo caduto in fondo al mare, macina le rocce e la sabbia creando un vasto gorgo, il Maelstrom, («la corrente che macina», dal verbo “mala”, «macinare»), ritenuto una delle vie che conducono alla terra dei morti. Questo nucleo di immagini, come rivela una serie di fatti, rappresenta un processo astronomico, lo spostamento secolare del Sole attraverso i segni dello zodiaco che determina le età del mondo, assommanti ciascuna a migliaia di anni. Ogni età porta con sé un’Era del mondo, un Crepuscolo degli Dei: le grandi strutture crollano, diluvi e cataclismi annunziano il plasmarsi di un mondo nuovo.

(…)

Oggi, la Precessione è un fatto assodato, immune da ogni complicazione che non ha armai più alcuna attinenza alle nostre vicende. Una volta, invece, era l’unico maestoso moto secolare che i nostri antenati potevano tenere presente quando ricercavano un vasto ciclo che interessasse l’intera umanità. D’altra parte i nostri antenati erano astronomi e astrologi. Essi credevano che lo slittamento del Sole lungo il punto equinoziale incidesse sulla struttura del cosmo e determinasse una successione di età del mondo posto sotto segni zodiacali diversi. Avevano trovato un grande piolo a cui appendere le loro riflessioni sul tempo cosmico, il quale recava tutte le cose nell’ordine prescritto dal fato. Oggi quell’ordine è venuto meno, così come è venuta meno la stessa idea di cosmo. Esiste solo la storia, felicemente definita come «una cosa, e poi un’altra, e poi un’altra…»

G. de Santillana, H. von Dechend, Il Mulino di Amleto, Adelphi, p. 22 e p. 94

Dunque, in un senso archeoastronomico, è del tutto evidente che nel passato i “diluvi” intesi come mutamenti astronomici del cielo, o come “affondamenti” di certe costellazioni sotto il piano dell’eclittica, debbano essere stati senz’altro più di uno. Ed è proprio a fenomeni di questo genere che accenna Platone, quando afferma che gli Egizi del suo tempo conservavano la memoria di molti diluvi. A sua volta, tutto questo significa che nel Timeo si è conservata una tradizione di osservazione del cielo stellato, durata decine e decine di millenni. E’ infatti questo il tempo che occorre per vedere Orione raggiungere più volte il punto più basso a Giza e poi quello più alto, che è quello che vedranno fra circa 300 anni i nostri pronipoti. Ed è proprio questo che rende ragione dell’associazione, solo apparentemente anacronistica, fra il simbolo astronomico di Cosquer con il geroglifico Antico Egizio, che non sembra altro che una sua derivazione (ma, più probabilmente, entrambi questi simboli derivano da un archetipo molto più antico).

Certo, se ci riferiamo alle ere del rock o a quelle dell’alta moda, i simboli possono pure cambiare una volta l’anno: ma quando le culture si rivolgono a cicli astronomici virtualmente eterni, lo stesso simbolo, almeno quanto ai suoi tratti essenziali, è facile che duri migliaia, a o anche decine di migliaia di anni. O ancor di più.

6.

Una volta che ne abbiamo compreso il codice, il significato dei miti cosmologici che compaiono in tutte le culture del mondo, compresa la nostra, comincia a svelarsi. In certi casi, non sembra nemmeno eccessivamente complicato. Per esempio, nelle radici mitiche dell’Occidente, nella cultura norrena troviamo Bergelmir, l’unico dei giganti che sopravvive al diluvio causato dal sangue di Ymir, che viene posto sotto la macina di un misterioso mulino. Le sue ossa vengono ridotte in polvere: ma anche in questa situazione riesce a generare figli ai giganti. In un mito simile, che troviamo nel Sudamerica precolombiano, un “osso sacrificale” viene finemente triturato nella mola dalla dea Ciuacoatl e la polvere viene quindi posta nella “coppa dei gioielli”. A questo punto gli dèi si procurano delle ferite e fanno fluire il sangue del loro pene nella coppa. Da questa mistura viene formata l’umanità.

Ma questo “mulino” non è altro che l’asse polare della terra, e la divinità non è altro che la stella polare su cui, astronomicamente, va ad “appoggiarsi”. La “coppa dei gioielli”, o, usando un termine caro all’Occidente, il Santo Graal, non è altro che il cono tracciato dalla rotazione dell’asse polare della terra attorno a quello dell’eclittica, che viene paragonato a un recipiente (altre volte viene paragonato a un albero, oppure a una colonna, o a una divinità con una gamba sola, etc.). L’angolo di questo cono varia da un minimo di circa 43 gradi a un massimo di circa 47. Un angolo vicino a quello medio di questo cono, o “coppa”, è quello che gli Antichi Egizi hanno usato per costruire la Piramide Rossa e la Piramide Romboidale che, in effetti, vista rovesciata, sembra proprio una coppa

La croce di Cristo, all’epoca in cui il cristianesimo cominciò ad espandersi nel nord dell’Europa, venne definita “un albero”. Ma quella dell’albero era appunto, come si è accennato sopra, una delle metafore tipiche dell’asse dell’eclittica, e anche quella compare puntualmente nei miti norreni, proprio come in quelli Maya o di migliaia di altre culture. L’albero dell’eclittica è “l’Albero della Vita” perché mettendo magicamente in moto i cerchi celesti, genera l’universo e tutto quel che contiene. Nella mitologia celtica, il Graal, cioè il cono dell’eclittica, è spesso rappresentato come una pentola che produce interminabilmente ogni sorta di primizie. Il paragrafo numero 25 del Tao-Thè-King si riferisce al polo dell’eclittica in quanto centro magico che fa ruotare il cerchio del cielo e che quindi, siccome la vita è mutamento, è il fondamento immobile della nascita, la crescita, la decadenza e la morte di tutti gli esseri

“C’era qualcosa di caotico e perfetto prima che il cielo e la terra nascessero. Silenziosa, vuota, sta da sola e non cambia. Gira intorno instancabile. Si può considerare la madre dell’universo.

Io non conosco il suo nome ma la chiamo con l’appellativo di «via». Sforzandomi di classificarla la chiamo «grande». «Grande» significa «oltrepassare»; «oltrepassare» significa «andare lontano»; «andare lontano» significa «tornare».

Quindi: la via è grande, il cielo è grande, la terra è grande, anche l’uomo è grande. Nell’universo ci sono quattro (cose) grandi, e l’uomo è una di queste.

L’uomo ha per modello la terra; la terra ha per modello il cielo; il cielo ha per modello la via; la via ha per modello sé stessa.”

Il punto del polo dell’eclittica non è segnalato da nessuna stella. Dunque può essere definito silenzioso e vuoto, come lo è un abisso. Gira sempre intorno a sé stesso instancabile e si può tranquillamente considerare la madre dell’universo, se si ha una visione metafisica per cui il centro è l’origine, cioè la madre del cerchio. A Chauvet, come abbiamo visto in The Snefru Code parte 6, gli uomini che hanno dipinto la Cappella dei Leoni e dei Rinoceronti condividevano questa visione del mondo, dato che sulla formazione rocciosa a forma di fuso che pende nel centro della grotta, che simbolizza il cielo del nord e il cono della precessione, hanno appunto dipinto un utero. In due rilievi del paleolitico, scolpiti sulle pareti di una grotta, il cono viene immediatamente identificato con la donna e i genitali femminili. Sulla Pietra di Narmer, il Sole dell’equinozio, che con “casa” dello zodiaco su cui sorge segna il mese dell’anno divino, è quel cerchio vuoto che viene tracciato dai leoni con il collo di serpente: ma, in senso mitico-astronomico si giunge all’era del Leone, che a Giza è simbolo dell’inizio e della fine di un ciclo precessionale, solo e soltanto se trascinati dalle spire del serpente, che altro non è che il ruotare del Drago. Si noti la straordinaria somiglianza fra il profilo della Pietra di Narmer e quello della roccia stalattiforme di Chauvet

7.

Queste digressioni che abbiamo appena concluso, verso il Paleolitico e verso la cultura Cinese, naturalmente, non sono affatto digressioni. Infatti, è solo nel rapporto con quest’antica forma della civiltà, fondata sull’osservazione delle stelle, che può fino in fondo disvelarsi il significato del paesaggio sacro di Giza, che è il tema principale del nostro lavoro.

Sopra abbiamo visto che, nella visione del mondo di queste culture, il Sole non è un’entità che mantiene un’identità costante. Muta col trascorrere dei millenni e col conseguente mutare del segno zodiacale su cui si leva all’equinozio di primavera. Dunque i soli si susseguono, nascono e muoiono. E la loro nascita si deve a quella grande vagina cosmica che è il cono dell’eclittica, abisso che è destinato poi ad inghiottirli, per dargli poi di nuovo un’altra vita, un’altra nascita, per l’eternità: questo e non altro è il significato di quegli enigmatici “dèi mortali” che si trovano sparsi nei racconti sacri di tutto il mondo, Bibbia compresa.

Nel Salmo 82 Elyon (“colui che sta più in alto”) dice agli “Elhoim” (plurale di un termine che dovrebbe essere l’equivalente del babilonese “Signori”) che “si è vero, voi siete degli Elohim figli di Elyon, ma ricordatevi che dovrete morire come tutti gli Adam” (cioè come tutti gli uomini). Se questi Elhoim sono configurazioni celesti legate allo zodiaco, è del tutto chiaro che sono destinate a morire. E’ solo che la loro vita dura talmente a lungo rispetto a quella degli Adam che gli Adam tendono a considerarli immortali. Scrivono a questo proposito de Santillana e von Dechend che nel mondo antico, dominato da religioni di ispirazione astronomica, all’equinozio di primavera

“La costellazione che sorgeva a oriente immediatamente prima del Sole (cioè quella che sorgeva eliacalmente) segnava il «posto» dove il Sole sostava. Veniva allora chiamata «portatrice» del Sole e principale «pilastro» del cielo“.

In questo senso, possiamo dire che veniva instaurato un rapporto simbolico fra le costellazioni equinoziali – cioè quella in cui il Sole sorgeva all’equinozio di primavera e quella in cui tramontava all’equinozio d’autunno – e l’asse dell’eclittica. Siccome Gesù era associato ai Pesci, perché era vissuto appunto al sorgere dell’Era dei Pesci, ecco che la sua croce venne associata all’albero divino, cioè al pilastro del cielo: perché in quel momento l’albero divino, cioè l’asse dell’eclittica (e forse anche quello polare) tendeva a identificarsi con la costellazione su cui il Sole sorgeva all’equinozio di primavera.

Ma in tempi antichissimi, il Gran Dio dei Galli, Uno e Inconoscibile, era chiamato Belen, perché il Sole, nella sua corsa precessionale, all’equinozio di primavera passava nella costellazione dell’Ariete, che in gallico e in alto francese si chiamava “bélin”.

Louis Charpentier, I Misteri della Cattedrale di Chartres, Edizioni Età Dell’Acquario, p. 22

Sembra chiaro: l’asse dell’eclittica, nell’ambito delle antiche religioni astronomiche, era visto come una divinità che rimaneva, nella sua sostanza profonda, eternamente la stessa. Quello che era destinato a mutare era il modo con cui si manifestava all’uomo, che andava con il mutare della costellazione su cui il Sole via via va a sorgere all’equinozio di primavera. Un mutamento che ha luogo una volta ogni 2160 anni circa

Ma con il nostro lavoro abbiamo scoperto la sezione aurea di un ciclo precessionale, e forse anche di altri cicli, doveva avere in certi casi un’importanza simbolica altrettanto importante che il suo inizio e la sua fine. O piuttosto: nell’ambito del cerchio divino della precessione, i diversi cicli si strutturano secondo numeri e ritmi sacri. Il cerchio si suddivide in segmenti, e questi segmenti si intersecano secondo un codice musicale, quello che i pitagorici chiamavano “l’armonia delle sfere”. La struttura del paesaggio sacro di Giza ce lo dimostra molto chiaramente. Per altro verso, in questa direzione ci spinge anche il buon senso, dato che è difficile immaginare che un periodo di tempo tanto lungo non abbia altri segmenti che quelli dettati dallo zodiaco.

8.

Un anno solare, dunque un anno umano, è fatto di mesi, ma anche di stagioni, di settimane, di giorni, di ore. In un anno solare la luna nasce e muore molte volte, mentre i cicli dei pianeti vanno avanti. Questa deve essere, in un certo modo, anche una caratteristica dell’Anno Divino, se l’Anno Umano altro non è che un suo riflesso. Per esempio, nei circa 2160 anni che dura un mese precessionale molte altre cose accadono nel cielo, i mutamenti sono lenti, e tale lentezza era probabilmente accompagnata da momenti di attesa, da riti di passaggio, da simboli.

Fra il punto più basso di Orione all’orizzonte e il passaggio alla nuova stella polare intercorreva appunto un tempo legato alla sezione aurea di un semiciclo precessionale. E questo tempo, con le geometrie astronomiche connesse, doveva assumere un significato sacro, come sacro doveva essere sentita la partizione un intero ciclo precessionale ottenuta per mezzo del numero di Eulero o del numero d’oro. A un punto tale che, come abbiamo già visto in altri lavori precedenti, l’inclinazione del tetto della Camera della Regina sembra pensato proprio per alludere a questo periodo di tempo. Questo angolo, con tutto il suo significato simbolico e, probabilmente, con parte del suo significato scientifico, è stato usato anche dagli ignoti ideatori dell’allineamento di San Michele che, proprio come quelli del Circolo di Nabta Playa, è capace di individuare dei punti cruciali nel diagramma dell’atomo di idrogeno di Bohr

Molto significativamente ritroviamo degli angoli connessi con la precessione e con la sezione aurea del ciclo precessionale anche nei dipinti che vediamo qui sotto. Due sono famosissimi, e hanno come tema la lancia di Longino che, con ogni probabilità, anche nel mito aveva un significato astronomico. Essa rappresentava l’asse terrestre che “ferisce” la stella polare su cui punta, e, perciò, anche la divinità che essa rappresenta. La sezione aurea di un ciclo o di un semiciclo precessionale, annunciano qualcosa di nuovo, ma anche la morte di qualcosa di vecchio

Ma, nel corso di questo lavoro, abbiamo mostrato come la sezione aurea, oltre a connettersi con cicli cosmici ritenuti sacri, è anche uno dei fondamenti del sistema matematico con cui si può descrivere l’universo. Dunque, quando nei miti cosmologici sparsi in tutto il mondo e in tutte le culture troviamo che dei numeri sono sistematicamente connessi con il sacro (come il 70, il 360, il 72, il 18, il 54, il 3, il 4, il 5, il 6 etc.), non ci troviamo di fronte a un codice numerico legato essenzialmente ad un’astronomia “primitiva”, legata all’osservazione del cielo ad occhio nudo. Al contrario, proiettando quei numeri sul sistema trigonometrico, abbiamo avuto la possibilità di gettare lo sguardo su una fisica e su una matematica avanzatissime, addirittura su una teoria dei campi unificati , appartenente però a una scienza che ben poco aveva a che fare con la nostra, tanto nelle sue immagini allegoriche che nella sua forma matematica.

Capitolo 14:

LA RELIGIONE ASTRONOMICA PALEOLITICA E POST PALEOLITICA NELL’ARCHEOLOGIA DELL’OCCIDENTE AL SUO CREPUSCOLO

1.

In relazione al lavoro che abbiamo svolto in quest’articolo, tutto quel che abbiamo visto fino ad adesso significa che l’Alto e Basso Egitto non sono altro che il cielo sopra e sotto l’equatore celeste, e che la loro unificazione è un evento astronomico e null’altro. Andare a cercare nel mito dei fatti storici in grado di “spiegarlo” è il modo migliore del mondo per lanciarsi in una catena di fraintendimenti che non porta da nessuna parte. Forse, l’unica strada più sbagliata di questa è sottoporre il mito alla cinica dietrologia tipica del giornalismo politico. Con gli occhi fissi sul’attualità o sulla storia recente del nostro mondo, dove vediamo continuamente che i politici “raccontano storie” per manipolare l’opinione pubblica, e non certo per dargli un’istruzione, quando ci volgiamo alla storia possiamo essere tentati di vedere in libri come il Pentateuco o nelle steli e nei papiri Antico Egizi dei riflessi delle vicende storico politiche di un mondo simile al nostro. Quindi, siamo pronti a proiettare su vicende che riguardano un cambio di dinastia, o il destino di un sommo sacerdote o di un generale, gli stessi schemi interpretativi che adottiamo, con ogni sorta di buona ragione, nel nostro presente storico. Questi schemi interpretativi si possono riassumere peraltro in un modo molto semplice. Se un von Clausewitz ha anticipato i tempi suggerendo che la guerra non è altro che una prosecuzione della politica con altri mezzi, noi adesso possiamo completare la filosofia implicita nel suo aforisma dicendo che, a sua volta, la politica non è altro che una prosecuzione del bunga-bunga con altri mezzi.

Il quotidiano ripetersi di episodi di corruzione, il sistematico prevalere degli interessi egoistici su quelli generali, l’uso opprimente e sistematico dei mass media per propagandare bugie negli interessi di questo o quel potentato economico-politico, ci spinge a pensare che le cose siano sempre andate così. E così proiettiamo addirittura nel passato ancestrale dell’umanità, in un mondo dominato dall’ermetismo e dalla tradizione orale, la degenerazione consumista di ciò che fu la politica. E non ci potrebbe essere errore più grossolano. Il mito cosmologico, almeno nei tempi antichi, non fu il frutto dell’astuzia di persone che, consapevoli delle leggi quantitative della fisica, le usavano per esercitare un potere assoluto su gente ignorante e superstiziosa, capace di deglutire qualsiasi frottola gli si raccontasse come un bicchiere d’acqua fresca. Questi sono fenomeni tipici della società di massa, non di quel mondo.

Ci basta contemplare un paesaggio sacro come quello di Giza – con il labirinto di allusioni delle sue simmetrie, con la sua oltreumana imponenza, con la maestosa e quasi irreale perfezione della sua realizzazione tecnica – per rimanere certi che coloro lo hanno progettato e costruito credevano fermamente, per esempio, che Orione e il Toro fossero delle divinità possenti e terribili, che la loro posizione nel cielo – o piuttosto: nel Regno dei Cieli – determinasse gli eventi che accadevano sulla Terra, che del Regno dei Cieli veniva creduta uno specchio.

L’idea che la religione sia un oppio dei popoli corrisponde per noi a una verità eterna, frutto del progresso della scienza: è invece il frutto marcio di civiltà vecchie e decadenti, che hanno del tutto esaurito la loro spinta spirituale. In esse l’irreligione e il materialismo prendono piede fino al punto che non solo non si crede più alle visioni metafisiche che pure furono il loro fondamento: non si crede più nemmeno che in passato ci sia mai stato qualcuno che le abbia potute credere. Il Don Chisciotte, una delle opere che danno inizio alla modernità, è una sorta di burlesca sepoltura degli ideali cavallereschi del Medio Evo: ma questo tema, a ben vedere, è lo stesso del Macbeth o dell’Amleto, come dei Pensieri di Pascal (sia pure in modo più complesso). E che la modernità rappresenti la vecchiaia dell’Occidente lo si capisce dal fatto che inizia con questi per quanto letterariamente splendidi funerali.

Sotto il cielo vuoto del ‘600 gli ideali della nobiltà medievale sono diventati talmente estranei alla mentalità corrente che Cervantes non riesce a immaginarli altro che come una fantasia delirante degna di un pazzoide. Eppure, solo pochi secoli prima, il codice d’onore dei cavalieri era proprio quella di cui Cervantes si fa beffe. E non meno reali sono le gesta dei cadetti di Normandia, o dei Templari, che in situazioni di inferiorità numerica a volte davvero incredibili sono riusciti ad avere ragione del nemico. Simili in questo ai 300 Spartani e agli altri due o tremila Greci che riuscirono a tenere in scacco la superiorità numerica dell’esercito di Serse alle Termopili, finché non si trovò il modo di circondarli. Dunque, come mai tutta questa voglia di ridere degli eroi del passato, che sono esistiti proprio come esistono le bassezze e il cinismo della modernità? In che senso possiamo trattare dall’alto in basso gente come i cavalieri medievali e il loro codice d’onore, che essi rispettavano ancor più che i dettami della morale religiosa? Cosa c’è da ridere di uomini la cui parola valeva più di cento atti notarili della modernità?

2.

Cervantes ride, e noi con lui,come ogni volta forse si è riso nel momento in cui ci si è resi conto che visioni metafisiche possenti, che si sono credute eterne ed immutabili, invecchiano, muoiono, e altro non ne resta che il cadavere imbellettato e pronto per la sepoltura. Ideali di fronte a cui si tremava e a cui si era pronti a piegare in ogni istante le ginocchia si sono ridotti a un mantello d’ipocrisia che copre il fatto che – nell’Occidente moderno come peraltro nella Roma di Tacito – tutto si fa per denaro. Il virtuoso Pisone “che aveva compiuto i trent’anni con più fama che fortuna“, nel suo discorso ai legionari, parte dal presupposto che appellarsi alle sue virtù per ottenere l’appoggio dei suoi uditori sia un puro e semplice flatus vocis. Così, con una retorica tanto alta quanto modesto era il suo scopo, si mostra ai legionari come alfiere del minor male

“Non voglio ricordare né la mia nobiltà, né le mie virtù. Non vale nemmeno la pena parlare di virtù, quando ci si mette in lizza con Otone, i cui vizi, sua sola gloria, hanno sconvolto l’impero anche quando era amico del principe. Forse che il suo aspetto, il suo portamento o la sua effeminata cura del corpo meritano l’impero? Coloro cui impone la sua prodigalità, sotto specie di liberalità, si ingannano. Otone sa dilapidare, non sa donare. Adesso il suo animo desidera soltanto stupri, banchetti e compagnia di femmine; crede che questo sia l’appannaggio del potere. Ma se la soddisfazione di ogni piacere sarà sua, il rossore e l’obbrobrio saranno di tutti. Nessuno infatti ha mai esercitato bene un potere acquisito col disonore. Galba è stato eletto con il consenso del genere umano, e Galba ha eletto me con il vostro consenso. Anche se patria, senato e popolo, sono armai dei nomi vani, è vostro interesse, camerati, che non siano i peggiori a nominare l’imperatore.”

Tacito, Storie, Libro Primo, 30.

Per avere un’idea del clima, chiamiamolo così, politico e culturale in cui un personaggio come Galba venne eletto imperatore “con il consenso del genere umano” possiamo andare a dare un’occhiata la libro settimo delle Vite dei Cesari di Svetonio. Inviato in Cantabria Galba

Governò quella provincia per otto anni in modo vario e ineguale. In un primo tempo fu aspro, energico e persino eccessivo nel reprimere i delitti. Infatti, ordinò di tagliare le mani e inchiodarle al banco, a un cambiavalute disonesto, e fece appendere alla croce un tutore per avere avvelenato il proprio pupillo dal quale doveva ereditare. Poiché questi aveva invocato la legge, dichiarandosi cittadino romano, Galba, quasi per alleviargli la pena con una consolazione e con qualche segno onorifico, diede ordine di sostituire la croce con una molto più alta delle altre e dipinta di bianco.

A poco a poco però, per non farsi notare da Nerone, diventò pigro e trascurato, perché, come diceva: «Nessuno deve rendere conto di ciò che non fa».

Svetonio, Vite dei Cesari, Libro Settimo, IX

Diciamoci la verità: l’imponente non meno che impotente retorica moralistica di Pisone – in un’epoca tanto incerta in cui perfino un Nerone poteva trovarsi nel giro di pochi minuti senza più un amico che lo aiutasse né un nemico disposto ad ammazzarlo – ricorda fin troppo facilmente quella con cui un certo genere di fustigatori dei costumi, nei tanto deprecati anni ’80, invitava a votare Dc “turandosi il naso”. Anni che, fra i tanti difetti che gli possiamo imputare, hanno avuto il pregio di essere migliori dei ’90, non meno che di quelli che dall’inizio del nuovo millennio ci hanno portato al triste presente, dove chiedere a un elettore di distinguere la mafia dalla politica è un po’ come chiedere a un pesce di distinguere il verme dall’amo a cui sta appeso. Perché negarlo? Già al tempo in cui Pisone pronunciava il suo discorso ai legionari, a Roma, vicende come quelle di Cincinnato, un tempo celebrate come esempio di una vita piena e veramente degna di essere vissuta, venivano tenute alla stregua di fiabe per bambini, un po’ come oggi lo sono in Italia il coraggio dei partigiani o la moralità di un La Pira o di un Berlinguer.

Tutti questi sono fatti innegabili, e nessuno li vuol contestare. Né si può sostenere che riguardino l’Italia in modo particolare ed esclusivo: riguardano tutto l’Occidente, sia pure con modalità diverse. Fino a qualche tempo fa, si sentiva dire in giro che Napoli era una caricatura dell’Italia, come l’Italia era la caricatura dell’Europa. Poi un giorno ci si sveglia e scopre che la proverbiale serietà, il teutonico senso del dovere, la perfetta organizzazione non meno che il prestigio dei Tedeschi sono stati utilizzati dal gruppo Volkswagen – Das Auto – per organizzare una truffa in perfetto stile napoletano su scala mondiale.

Ai tempi in cui Crasso accumulava ricchezze pari a un decimo circa del patrimonio imperiale, cittadini romani con tutti i diritti venivano gettati nelle fosse comuni perché non avevano denaro sufficiente per permettersi un funerale decente. Oggi la Apple, attraverso l’oculata gestione di un classico buddista di stile e scuola occidentali – buddisti di quelli che diventeranno vegetariani nella prossima vita – ha accumulato un capitale paragonabile al prodotto interno lordo di un’intera nazione andando a impiantare in Cina le famose “fabbriche dei suicidi”. Posti poco ameni, a quel che si capisce, dove però la gente, in omaggio al buddismo del loro fondatore, lavora talmente tanto e guadagna talmente poco che preferisce a un certo punto buttarsi dal tetto, dove a volte è costretta a dormire.

3.

In un clima di questo genere, sperare in un’inversione di rotta della nostra civiltà è un puro nonsenso, paragonabile a quello del pazzo della poesia di Caproni, che, per impedire il calare della sera, si mise di fronte al sole declinante a braccia spalancate gridando “Di qui non si passa!”.

Ma che un mondo spirituale invecchi e infine muoia non significa che non sia mai esistito. Gli Spartani che eressero una lapide alle Termopili, a eterna memoria dei loro 300 eroi, morti per la Legge, sono stati ridicolizzati dal Tempo prima ancora che dall’edonismo di stile epicureo. Questo è vero, e nessuno si sogna di negarlo. Ma anche l’epicureismo è stato infine ridicolizzato dal Tempo. Un migliaio di anni dopo le sue esortazioni al quieto vivere, nel Medio Evo della nobiltà guerriera, era tanto facile trovare un cavaliere interessato alla tranquillità dello spirito tanto quanto negli anni della “Milano da bere” era facile trovare un assessore alla cultura socialista che si interessasse effettivamente alla cultura. Infine, anche il nichilismo attuale, che si crede verità incrollabile, termine ultimo dell’Evoluzione, tramonterà nell’alba di un nuovo mondo spirituale, giovane ed entusiasta, destinato anch’esso un giorno a tramontare nell’alba di un nuovo materialismo.

A ben vedere, che gli ideali etici siano sempre e comunque proclamati ad usum delphini, che la religione sia sempre e comunque da considerarsi come un oppio dei popoli, che i nobili siano sempre fannulloni e il popolo sempre bue, non sono affatto delle verità eterne. Queste sono, al contrario, le idee preconcette che se ne fa lo storico occidentale medio. Nato e cresciuto nel pieno della decadenza della sua civiltà, immerso in un materialismo consumista che fin dalla più tenera infanzia spegne in lui ogni barlume di vita spirituale, non riesce a immaginarsi che in altre epoche si potesse credere a Dio o agli dèi con la stessa innocente sincerità con cui lui crede, per esempio, al prodotto interno lordo, al libero mercato, al progresso della tecnica o altre amenità del genere. Noi ci crediamo intelligenti e disincantati, perché non crediamo in Dio, non facciamo offerte all’oracolo di Delfi e non manteniamo a caviale e champagne la casta dei sacerdoti e degli aruspici. D’altra parte, spendiamo cifre la cui enormità è difficilmente quantificabile per istruire e mantenere la casta degli economisti che, da quando esiste, ha previsto tutto meno quello che di fatto poi è accaduto. Un libro dal titolo “La Fine della Storia” ha venduto decine di milioni di copie e fatto la fortuna del suo autore proprio nel momento in cui la storia si è svegliata, si sgranchita le gambe e ha cominciato a rovesciare stati, dividere nazioni, sfasciare economie, dichiarare guerre, suscitare rivolte come in tutto il secondo dopoguerra non era mai accaduto.

4.

Noi siamo convinti di essere i primi nella storia a vedere nei rapporti umani e politici solo il pretesto di quella che Nietzsche ha definito “volontà di potenza”, e razionalizziamo il nostro nichilismo con l’idea che noi siamo “progrediti” e sappiamo come vanno le cose a questo mondo. Coloro che in passato credevano a Dio, agli dèi e agli ideali erano invece dei poveri idioti. In questo senso, il nichilismo moderno è un’illusione ancor più profonda di quelle che crede di smascherare. Forme diverse di disillusione e di materialismo, lungi dall’essere un frutto dell’evoluzione dell’intelletto umano, sono un fenomeno tipico di tutte le civiltà invecchiate.

Ancor prima della conquista Romana, un paio di secoli dopo la vittoria del Davide greco contro il Golia persiano, Epicuro diventò un filosofo di successo, destinato a influenzare anche i futuri conquistatori con una dottrina che sosteneva che la felicità consistesse sostanzialmente in una vita tranquilla. Il piacere consiste per lui nel soddisfare i bisogni naturali e necessari, cioè nel mangiare e bere quando e per quanto si abbia fame o sete e non di più. D’altra parte, si nota che mangiare quando si ha fame e bere quando si ha sete è quel che fanno gli animali, senza bisogno di alcun insegnamento filosofico: dunque, da questo punto di vista, possiamo notare che Epicuro, cosciente o meno che ne fosse, sostiene che la condizione animale è per natura superiore a quella umana. La conoscenza per lui è utile perché libera dalla paura degli dèi e da quella della morte: in questo senso Epicuro esalta di nuovo la condizione degli animali, che, grazie alla loro ignoranza, non hanno bisogno che alcuno di un filosofo che gli spieghi che la morte non c’è fin che ci siamo noi, o che gli dèi sono troppo felici per aver tempo di pensare agli uomini. Quanto allo stato e alle sue leggi, Epicuro si mette dalla parte della stato, ma non perché infrangere la legge sia da considerarsi ontologicamente come un male. Non si deve andare contro la legge perché poi si deve temere la vendetta della società che l’ha promulgata: come se al mondo non ci fossero dei criminali che si vendicano dell’onestà e del rispetto delle leggi in modo più crudele della legge.

Si leggono cose di questo genere e, davvero, si rimane esterrefatti. Quasi non si riesce a immaginare che a Platea i Greci litigassero per occupare la prima fila e il lato destro della falange, il posto più pericoloso e dunque quello in cui fosse maggiormente probabile conseguire lo scopo della vita: la morte gloriosa in battaglia per la difesa della patria. Ai tempi della conquista romana un filosofo epicureo, deportato a Roma per fare il maestro in una famiglia di patrizi, annotava stupefatto che la religione dei suoi carcerieri sembrava fatta apposta per tenere sottomesso il popolo: come era possibile che la gente non se ne accorgesse?

Che una persona minimamente istruita o minimamente dotata di buonsenso potesse davvero credere agli dèi era un pensiero per lui assolutamente inaccessibile. Tanto inaccessibile quanto per i suoi compatrioti di un paio di secoli prima lo era, per esempio, il pensiero che si potesse infrangere la tregua Olimpica, o farsi beffe dell’oracolo di Delfi, senza dover temere l’ira degli dèi.

5.

Ma, appunto: un certo tipo di atteggiamenti “disincantati” non sono frutto del conseguimento di una verità oggettiva, ma solo di un certo tipo di pregiudizi culturali, legati a una situazione storica particolare e come tutte le altre transeunte. Il nichilismo non ha una sostanza storica più duratura delle fedi religiose di cui si fa beffe. Una volta che ci togliamo un certo genere di occhiali con paraocchi incorporato, basta che ci spostiamo di qualche migliaio di chilometri e ancora oggi si trovano centinaia di milioni di persone che fondano la loro vita personale non meno che quella della loro nazione su idee religiose e metafisiche fortissime, per cui sono tranquillamente disposti a uccidere come a morire. Questo ci dà un’idea di come doveva essere l’Occidente un migliaio di anni fa, quando non c’era quasi persona – eretici compresi – che non credesse in un Dio unico e trascendente. O, per tornare al nostro argomento principale, di come doveva essere l’Egitto ai tempi della cosiddetta IV Dinastia. Lungi dall’essere degli spacciatori di “oppio dei popoli”, coloro che hanno costruito le Piramidi dovevano essere delle persone che credevano fermamente che gli avvenimenti importanti fossero quelli che si verificavano in cielo notturno e diurno inteso come un “Regno dei Cieli”. Gli avvenimenti che si verificavano nella storia comune, quando pur venivano presi in considerazione, erano sistematicamente intesi come epifenomeni degli avvenimenti della storia celeste.

In effetti, se c’è una cosa che Bauval dimostra con il ragionamento che svolge nelle pagine che abbiamo citato precedentemente, è che il paesaggio sacro di Giza e dintorni esisteva già da molti millenni, quando nel 2080 Aldebaran e Epsilon Taurus «emergono» al di sopra dell’equatore celeste. In quella data si racconta che «le Due Terre» – cioè l’Egitto-Duat che è nei cieli e l’Egitto che si trova sul nostro pianeta – si uniscono. Ma questo non accade perché un faraone vince una guerra, o perché un sacerdote cinico e istruito porta a termine un colpo di stato usando come leva la superstizione altrui.

Al contrario, l’evidenza che emerge è che l’unione delle «Due Terre» si verifica nel momento in cui le due piramidi di Dashour – ovvero quella parte della gigantesca meridiana precessionale che è il paesaggio sacro costruito intorno a Giza che rappresenta le Iadi – va a collimare con la situazione astronomica che si è appena verificata, ovvero con «l’emersione» di Aldebaran e Epsilon Taurus al di sopra dell’equatore celeste.

Si tratta dunque di mutamenti cosmici che vengono descritti in termini di avvenimenti terreni, ovvero di una disputa per il trono, o di un mutamento di Dinastia, che però, con ogni probabilità, non aveva nulla di nulla a che fare con quel che effettivamente succedeva nell’Egitto terrestre. Quando noi cerchiamo in miti come quello che spiega l’unificazione dell’Alto e Basso Egitto delle tracce di quello che accadde a livello politico nella società egiziana del tempo, siamo destinati inesorabilmente a prendere lucciole per lanterne. Perfino Bauval, a dispetto di tutto quel molto che ha capito del pensiero religioso-astronomico dell’Antico Egitto, non rinuncia a interpretare secondo lo stile occidentale moderno il passaggio dalla IV alla V Dinastia.

Il papiro Westcar ha preservato un’antica leggenda concernente la V dinastia che, ci viene detto, sorse dopo che un’alta sacerdotessa di Eliopoli era stata fecondata da Ra, il dio Sole. Questo era un tipico artificio usato quando era in preparazione un cambiamento dinastico o un colpo di stato. Per esempio, Olimpia, la madre di Alessandro il Grande, asserì che Zeus-Ammon si era unito a lei, facendo di suo figlio il legittimo pretendente al trono di Macedonia e di Grecia; Cesare, dal canto suo, proclamava una discendenza da Venere generatrice. L’intervento divino nelle dispute dinastiche era un mezzo semplice per indurre la credula popolazione a prestare fede a una pretesa dubbia o perfino illegittima al trono. Una nascita «miracolosa» era sempre efficace: perfino nel XVII secolo in Europa, andava ancora forte. Di Luigi XIV di Francia, per esempio, si disse che era stato concepito miracolosamente, quando, dopo una sterilità durata ventisei anni, Luigi XIII e Anna d’Austria concepirono un erede «solare», soprannominato Dieudonné (donato da Dio).

La pretesa di un concepimento solare nel grembo della sacerdotessa di Eliopoli era probabilmente un sotterfugio abilmente orchestrato. A quanto pare il trucco funzionò. Secondo il papiro Westcar, Ra scese sulla terra e inseminò la moglie fin troppo compiacente dell’alto sacerdote di Eliopoli. Da quell’unione, nacquero tre gemelli, tutti destinati a diventare re d’Egitto: Userkaf, Sahura, e Neferirkara. Nel caso del papiro Westcar, come nel caso della Teologia menfita, io credo che abbiamo a che fare con un evento storico, spiegato in termini cosmici, da cui scaturì l’ascesa della V dinastia.

R. Bauval, A. G. Gilbert, Il Mistero di Orione, TEA, pp. 175-176

6.

Qui Bauval, dopo averci dato nelle pagine precedenti una lezione di archeoastronomia di livello altissimo, senz’altro il massimo capolavoro finora realizzato da questa giovane scienza e che resterà a fondamento di tutti i suoi futuri sviluppi, ci dà poi purtroppo un esempio di come i nostri pregiudizi culturali possano inquinare la comprensione di genti che, quanto alla storia e al senso della storia, la pensavano in modo radicalmente diverso dal nostro. Bauval, in un certo senso, ha capito tutto. Ha capito che per queste persone i corsi e ricorsi del cielo, e in particolare quelli del moto precessionale, erano tanto importanti da dedicare ad essi il più meraviglioso paesaggio sacro che l’umanità abbia mai concepito. Poi però non crede alla sua stessa teoria, e si spiega il mito (il mito: cioè la rappresentazione in codice di mutamenti cosmici) con avvenimenti mondani, per di più di bassa lega.

Noi non ci rendiamo conto che applicare a mondi spirituali tanto antichi e tanto lontani dal nostro le categorie interpretative della modernità conduce a un sicuro fraintendimento del loro senso profondo. Pensando agli intrighi di palazzo, all’ipocrisia, alle truffe ai danni all’opinione pubblica sapientemente orchestrate dai potenti delle nostre “democrazie” noi ci dimentichiamo che, per esempio, la moglie del sacerdote e il sacerdote stesso nell’Antico Egitto sono anche quelle stesse divinità stellari che rappresentano. E lo sono proprio nello stesso senso in cui oggi i cattolici considerano il papa il successore di Pietro, cioè il legittimo proprietario delle Chiavi del Regno. Dunque il papa, pur essendo un altro, è anche Pietro stesso: i simboli che indossa e che stringe nelle mani lo possiedono e lo trasfigurano, e dal momento in cui ne è il portatore le parole che pronuncia acquistano un senso ben diverso per un cattolico, di quando era un cardinale e dunque infine una persona qualsiasi. Ora la sua volontà, che lo voglia o no, è una prosecuzione della volontà di Cristo stesso.

Se questo genere di trasfigurazione simbolica vale nella modernità laicizzata, anche se per una minoranza di persone, figuriamoci come dovevano essere sentite queste cose nell’Egitto della IV Dinastia. La sacerdotessa che nel mito viene ingravidata dal dio non è una donna ambiziosa con tendenze adulterine che rimane incinta non si sa bene di chi non si sa bene come e si inventa una balla per prendere il potere: questo è quello che, con ogni sorta di buona ragione, penseremmo noi se nel presente qualcuno raccontasse una storia simile. In effetti centinaia di predicatori televisivi statunitensi hanno messo insieme patrimoni fantastici usando la religione per convincere i telespettatori a fare offerte che sono state usate per ogni genere di scopo, meno che per scopi religiosi. D’altra parte, che cosa aspettarsi in un’epoca in cui la truffa – televisiva o meno – è diventata la regola occulta e incombente del commercio? Oramai si aspetta solo che il rapimento a scopo di estorsione diventi una forma di interazione umana socialmente accettata.

Ma se analizziamo il racconto Antico Egizio nei dettagli, subito ci rendiamo conto che il suo scopo è di tutt’altro genere, e che ben poco a che fare con le panzane a cui la modernità ci ha abituati. Se fosse stato costruito per raggirare i lettori, sarebbe stato aggiustato meglio. Il senso comune infatti esita a credere che tutti e tre i figli di questo parto gemellare arrivino a regnare, perché questo presuppone il fatto altamente improbabile che dei tre gemelli muoia sempre e comunque quello che detiene il trono. Ma in un mondo tanto cinico e disilluso come quello preconizzato dalle nostre categorie interpretative si fa fatica a credere che il gemello diventato faraone non si sbarazzi il prima possibile di pretendenti tanto pericolosi di un trono conquistato con l’inganno.

Al contrario, nulla di più facile che il passaggio dalla IV alla V Dinastia, il cui inizio si colloca proprio intorno alla data indicata dai Pozzi Stellari della Grande Piramide (circa 2500 a.C.) e dunque alla sezione aurea di un semiciclo precessionale, non sia altro che il passaggio da una configurazione celeste all’altra. Quella che viene chiamata “IV Dinastia” potrebbe essere quella che abbiamo individuato come la sezione aurea di un semiciclo precessionale, ovvero i circa 8034 anni che vanno dal 10.500 a.C. fino al 2465 a.C. Alla fine del semiciclo precessionale mancano da quel momento 13000 – 8064 = 4936 anni. Con ogni probabilità la V Dinastia rappresenta un intervallo di tempo fra l’Antico Regno, e quello che viene chiamato Medio Regno, momento di passaggio a livello astronomico, e dunque connotato da ambiguità e confusioni che, di nuovo, non hanno nulla a che fare con la storia comune, ma con il mito e dunque con il cielo stellato inteso come un Regno dei Cieli.

7.

Intorno al 1000 a.C. nelle culture di tutto il Mediterraneo, dalla Grecia Micenea fino all’Egitto, si segnalano sconvolgimenti dovuti “a gente venuta dal mare”. Storici ed archeologi si sono rotti interminabilmente la testa – e magari anche qualche altra cosa – per cercare di capire chi fossero questi popoli. Gente, con ogni evidenza dedita alla pirateria e al saccheggio e capace di travolgere una zona del mondo vasta, popolosa, culturalmente molto evoluta, a cui la forza non mancava neppure a livello militare: di dove potevano essere saltati fuori, visto che il Mediterraneo a quel tempo pareva occupato quasi totalmente proprio da tutte quelle culture che essi riuscirono a travolgere?

Ma se abbandoniamo il nostro pregiudizio, che i miti siano un riflesso fantastico di eventi della storia comune, ecco che può balenarci in mente l’idea che quel “mare” non sia altro che la superficie dell’eclittica, e la gente che viene da quel mare non siano altro che delle nuove configurazioni celesti. Dèi un tempo forti e benevoli vengono annientati, oppure diventano malevoli. Equilibri astronomici, che per secoli hanno retto l’armonia divina scandita dai calendari sacri, di colpo si rompono: il Tempo diventa caotico. All’equinozio di primavera, il segno zodiacale che era “in carica” non è ancora uscito completamente dalla scena che appare all’orizzonte, né quello nuovo è ha ancora preso pienamente il suo posto. Oppure: certe stelle che si trovavano sotto l’equatore celeste ora lo sfiorano, così che ancora non sono né sotto e né sopra. Sono queste le situazioni confuse di cui si parla nei miti che, probabilmente, causavano angosce collettive di notevole entità. Ad essi dovevano esser connessi mutamenti il rinnovamento dei templi, o addirittura la loro distruzione e sostituzione con altri luoghi sacri: «Lascia il riposo! Scaccia il dolce sonno e pensa ai tempi a venire. Da oggi infatti datano nuove feste e nuove usanze perché stanotte è nato Shah Kay Khusraw!» si recita nel poema di Firdusi.

Lo ripetiamo: reazioni di questo genere a eventi che noi percepiamo come del tutto estranei alla nostra vita quotidiana ci sembrano del tutto assurde, e degne di malati mentali prima ancora che di esseri umani per quanto scarsamente evoluti. Che una persona seria ed istruita possa prenderli nella sia pur minima considerazione per un motivo diverso che il farsi una risata, ci sembra altrettanto pensabile di un Einstein che osserva febbrilmente i fondi di caffè per risolvere il problema del campo unificato. Aldebaran e Epsilon Taurus che emergono sopra l’equatore celeste: quale fatto possiamo considerare più vuoto e indifferente? di cosa ce ne può fregar di meno? quale fenomeno naturale possiamo considerare più ininfluente sulle vicende che si svolgono su “l’aiola che ci fa tanto feroci“?

Ma quando studiamo periodi storici tanto antichi, in cui dominava una visione del mondo radicalmente opposta alla nostra, dobbiamo abbandonare il nostro senso comune moderno – magari per riprenderlo in mano immediatamente nel momento in cui accendiamo la televisione e ascoltiamo un politico promettere che, quando avrà la maggioranza, ridurrà le tasse riducendo la spesa pubblica. Pensare che dietro discorsi di questo genere vi siano dei giochi di potere fini a sé stessi è tanto ragionevole quanto lo è pensare che nell’Antico Egitto avesse più peso sociale l’arrivo della Luna nuova che le spese per quanto faraoniche del Faraone (posto che l’Egiziano medio non ne fosse felice ed orgoglioso).

8.

Se ci ostiniamo a conservare dogmaticamente il nostro punto di vista, se ci rifiutiamo di prendere sul serio le idee altrui, la conseguenza inevitabile sarà che eventi importantissimi del passato vicino e lontano dell’umanità ci resteranno per sempre incomprensibili. A Gobekli Tepe troviamo un vasto complesso megalitico – realizzato in modo finissimo – che è stato seppellito dai suoi costruttori in una data – guarda caso – attorno al 10.500 a.C.: cioè intorno alla data in cui a Giza terminava un semiciclo precessionale che, con ogni probabilità, era considerato come la fine dell’intero ciclo precessionale. Lo sforzo compiuto per ricoprire queste grandi strutture – che sono, a quanto pare, un totale di 22, e occupano migliaia e migliaia di metri quadri di territorio in cima a una collina – fu enorme e di certo molto superiore a quello di costruirlo. Possiamo avere un’idea più chiara di quel che stiamo dicendo dando un’occhiata alle foto sottostanti

Vedendo queste immagini si rimane senza fiato. La quantità materiale coinvolto nell’opera di seppellimento di questo gigantesco impianto sacro sembra maggiore di quella che è servita a costruire la Grande Piramide. E in anni recenti in Francia, per riempire una cava d’argilla con un volume pari a quello della Piramide sono serviti 12 anni, al ritmo di un camion di sabbia ogni tre minuti per 10 ore al giorno.

A che un’opera di questa vastità, perché uno sforzo così immane per seppellire quelle strutture che tanti sforzi dovevano essere costate? La cava di pietra da cui centinaia di blocchi pesanti 5 o 6 tonnellate, e perfino alcuni pilastri di 15 tonnellate, vennero estratte e portate in loco distava circa due chilometri. Sforzi quasi inimmaginabili per erigere e sforzi ancora maggiori per seppellire: perché un atteggiamento che sembra tanto folle, da parte di gente che folle non doveva essere, se sapeva scolpire e collocare la pietra a quel livello che vediamo?

Una risposta sensata, sul momento, sembra impossibile: l’abisso dell’Assurdo si spalanca e, contrariamente ai costruttori di Goblekli Tepe, non abbiamo modo di poterlo ricoprire. Ma se abbandoniamo i nostri pregiudizi evoluzionisti e nichilisti la risposta la troviamo immediatamente.

Intorno al 10500 a.C. un Anno Divino finiva e uno ricominciava. Ma cosa si è fatto e cosa si fa ancora in molte parti dell’Occidente per celebrare la fine di un anno solare? Si bruciano, o si buttano via cose vecchie e se ne comprano di nuove. Ovvero: ci si libera simbolicamente dell’anno morto e dunque, simbolicamente, della morte. Ma questo era, per esempio, quello che facevano anche i Maya. Pop era il primo mese dell’anno Haab’, ed era perciò vissuto come il mese del rinnovamento. Tutti gli oggetti d’uso quotidiano venivano cambiati: si sostituivano abiti vecchi con abiti nuovi, mentre altri oggetti, come il vasellame o le stuoie, venivano proprio distrutti.

Questi usi sono talmente universali che è forse inutile fare altri esempi, se non quello che in questo momento ci riguarda, ovvero quel che è successo a Gobekli Tepe: una struttura destinata a segnare i mutamenti cosmici per la durata di un ciclo o di un semiciclo precessionale è stata seppellita per celebrare la sua morte. Non sappiamo invece cosa si sia fatto per celebrare l’inizio del nuovo Anno Divino. Forse in altro luogo si è dato inizio alla costruzione di una nuova struttura che, chissà, forse un giorno scopriremo, o che forse abbiamo già scoperto senza saperlo: come possiamo esser certi che il Plateau di Giza non nacque proprio per sostituire di Gobekli Tepe? Questa, ovviamente, non è nulla di più che una provocazione. Però rende l’idea del tipo mondo e di problemi con cui ci stiamo confrontando. Un mondo vasto e diverso, unito però da un culto millenario delle stelle, dedito ad osservare i mutamenti del cielo come segni di mutamento del Destino.

Infatti, di comportamenti del genere di quello che abbiamo incontrato a Gobekli Tepe ne troviamo traccia anche in Sudamerica. Il circolo di statuette che va sotto il nome di Offerta 4 o la gigantesca testa di granito, rappresentante un volto negroide, che vediamo qui sotto, vennero deliberatamente seppellite dagli Olmechi, un popolo che è un nome e nient’altro, attorno 1400 a.C.

Anche in questo caso, il deliberato seppellimento degli oggetti sembra avere un significato funebre: seppellire degli oggetti sacri connessi a un ciclo astronomico molto importante nel momento in cui questo ciclo finisce. D’altra parte, in quale altro modo potremmo spiegarci l’improvviso abbandono di intere città da parte dei Maya, che, a quanto pare, al momento dell’abbandono erano ancora in perfette condizioni?

È vero però che vi sono ipotesi alternative. Per esempio, qualcuno ha detto che vennero abbandonate nel momento in cui lo sfruttamento delle foreste a scopo edilizio li privò delle necessarie risorse alimentari. In ragione di ciò, furono costretti ad abbandonare le città, diventate oramai cattedrali nel deserto, e a disperdersi nei dintorni. Però, che gente strana questi Maya: tanto intelligenti da progettare una struttura in cui, il giorno dell’equinozio, il Sole disegna un serpente sulle scalinate. Tanto stupidi da non rendersi conto per costruirla stavano radendo al suolo tutte le foreste della zona.

Non si potrebbe credere che nell’antichità la gente fosse tanto stupida, se cose di questo genere non facessero il paio con le imprese di quei pittori del Paleolitico che, secondo l’ipotesi di un autorevole biologo evoluzionista, hanno cominciato a dipingere quelle strane immagini in fondo a grotte tipo quella di Chauvet perché, ovviamente, dipingere fa bene al cervello. Infatti, stimola le connessioni fra neuroni. Però, che gente strana questi pittori del Paleolitico: tanto evoluti da dipingere quelli che in certi casi paiono dei capolavori degni di esser messi accanto a quelli della pittura cretesi. Nello stesso tempo però ancora tanto vicini alle scimmie da non rendersi conto che avrebbero potuto “stimolare i collegamenti neuronali” dipingendo in luoghi più ameni che in fondo a degli intestini di pietra in grado di papparsi uno speleologo. Ambienti del tutto privi di illuminazione – tanto cara ai moderni pittori, forgiati da millenni di evoluzione – per di più frequentati da bestie feroci scarsamente inclini alla contemplazione estetica, perennemente affamate e in certi casi lunghe anche qualche metro.

9.

In effetti, imprese di un certo genere sono per noi talmente irrazionali che perfino nel contesto di un film di Walt Disney ci sembrerebbero non è chiaro se più ridicole o più assurde. Il che ci spinge a perdonare prontamente quegli intellettuali evoluzionisti che, nel tentativo di superare di slancio il baratro del nonsenso che di colpo si trovano davanti, si lanciano in ipotesi ancora più ridicole e assurde dei fatti che vorrebbero spiegare.

D’altra parte, agli occhi della mentalità evoluzionista, l’antica religione astronomica è un fenomeno che si presenta talmente incomprensibile che ci risulta filosoficamente consolatorio associare le pitture rupestri agli sport estremi della modernità, o l’abbandono di strutture ancora in perfetto stato a uno sfruttamento delle risorse naturali che arriva alla demenza (ma anche questo – c’è bisogno di ricordarlo? – è un fenomeno non meno moderno e attuale che gli sport estremi). Siamo disposti a qualsiasi di acrobazia logica o illogica pur di non spiegare i comportamenti umani con fenomeni tanto lontani dalla “lotta per l’esistenza” come i mutamenti celesti indotti dalla precessione. Abbandonare delle città perché le stelle sono cambiate? Questo ci sembra altrettanto logico che radere al suolo uno stadio di calcio perché la moglie del presidente ha minacciato che, in caso contrario, può darsi che cambierà pettinatura. L’uomo è una scimmia in lotta per l’esistenza, che il caso evolutivo ha dotato di strumenti tecnici in grado di condurla alla vittoria sulle altre specie: cosa c’entrano le del tutto inutili stelle e costellazioni che stanno lì in cielo tranquille e beate a non far nulla, con quelle utilissime clave, uno dei primi doni del caso evolutivo, con cui un duecentomila anni fa o giù di lì si prese a rompere la testa al prossimo e poi anche al successivo?

Questo è il nostro punto di vista: il punto di vista dell’evoluzionista stupito, che guarda agli usi e ai costumi di un mondo che dell’evoluzione non ne sapeva nulla e che, posto che ne avesse saputo qualcosa, l’avrebbe relegata al rango di una fiaba per bambini di secondo o terz’ordine. Al contrario, dal punto di vista di gente come i Dogon, gli atteggiamenti dei costruttori-distruttori di Gobekli Tepe come dei Maya sarebbero perfettamente comprensibili, per non dire assolutamente necessari. Infatti, il motivo per cui hanno colonizzato la loro terra e scacciato i suoi precedenti abitanti non ha nulla a che fare con la sua fertilità o con l’abbondanza della cacciagione, dato che si tratta di un luogo desertico, che mette duramente alla prova le loro capacità di sopravvivenza

I Dogon sanno benissimo che la zona situata tra i due tropici terrestri non è, delle terre abitabili, la più ospitale, così come lo sapevano i loro maestri dei tempi lontani, gli arcaici scienziati che coniarono la terminologia del mito. Ciò che contava era la fascia zodiacale tra i tropici celesti, che offriva le case e le locande, le « maschere » e i travestimenti, ai pianeti dai molti viaggi e dalle « mutevoli forme ».

L’enorme distanza fra questo punto di vista e la moderna indifferenza è quasi inconcepibile, se non per chi si rende conto di quanto sia vasta la voragine apertasi nella storia con l’adozione della dottrina copernicana. Ciò che per Sir Thomas Browne era un «O altitudo » affollato di emozioni religiose, di presenze e presentimenti, è diventato una piatta banalità capace, tutt’al più, di ispirare un cosmonauta sovietico e le trionfanti parole: « Sono stato in cielo e non ho trovato Dio in nessun luogo ». L’astronomia è caduta in basso: ora appartiene al regno della balistica esterna, materia per le avventure della Pattuglia dello Spazio.

G. de Santillana – H. von Dechend, Il Mulino di Amleto, Adelphi, pp.86 – 87

10.

La conclusione del nostro ragionamento sembra dunque inevitabile. Per lo storico moderno, è giunto il momento di sconvolgere la sua posizione ermeneutica e dunque, diciamo così, di relativizzare il relativismo e di abbandonarlo, per riuscire a identificarsi, almeno finché ha il capo chino sui libri o sui reperti archeologici, con la mentalità delle genti e delle culture di cui si occupa. E’ vero, oggi in Occidente quasi più nessuno crede veramente in Dio. Che gli astri siano dèi ci sembra addirittura una fanfaluca degna del pazzo ubriaco di shakespeariana memoria. Nel nostro mondo qualsiasi filosofo serio – per quanto scettico su qualsiasi altra cosa – ritiene che le profezie di aruspici ed astrologi stanno al futuro come le promesse elettorali rispetto alla politica, e chi la pensa in modo diverso di solito si scopre essere un assiduo frequentatore di reparti di psichiatria particolarmente vivaci.

Questa è la nostra vita, il nostro presente e nessuno si sogna di negarlo. Ma, se una cosa Freud è riuscito ad insegnarci, è proprio questa: che se proiettiamo il nostro materiale psichico e culturale sugli altri, siamo destinati a fraintenderli e dunque a ignorare per sempre il senso che essi hanno della loro identità. Ma, in questo caso, nella misura in cui fraintendiamo l’identità altrui, rischiamo di fraintendere anche la nostra. Infatti le teorie evoluzioniste si reggono su un presupposto tolto il quale sono destinate a crollare su sé stesse come un castello di carta. Questo presupposto possiamo esprimerlo facilmente in questo modo: che quanto più andiamo indietro nel passato, quanto più troviamo degli esseri umani simili alle scimmie da cui si sono evoluti. Esseri dunque privi di matematica e di scienza, con un’organizzazione sociale e un linguaggio primitivi, dotati di mezzi tecnici che in confronto a quelli di cui siamo dotati attualmente sono da considerarsi perfettamente ridicoli.

Questi esseri, quasi del tutto privi di coscienza, sono stati generati dal caso, che ha fatto sì che delle scimmie abbiamo cominciato a sviluppare un cervello che le ha spinte, per esempio, a considerare ciottoli e bastoni che trovava già fatti dalla natura come possibili strumenti in grado di aiutarlo nella caccia e nella lotta con altri esseri umani. Poi lentamente, per accumulazione di altre casualità, altrettanto banali e fatali che le estrazioni del lotto, queste scimmie hanno preso a raffinare i loro strumenti. Il loro cervello, inizialmente quasi identico a quello di un bruto tanto per volume che per efficienza, è cresciuto fino al punto che è culminato nella coscienza moderna, in cui un individuo istruito è addirittura capace di stendersi di recarsi da un dottore, stendersi su un divano e parlare dei propri stati mentali, e a interpretarli in ragione di esperienze infantili o di altro genere, nel tentativo di alterarne le dinamiche.

Dunque, gli esseri vicini alle scimmie stanno alla civiltà come l’infanzia sta al nevrotico, si potrebbe dire: sono uno stadio superato o da superare per poter accedere alla maturità, e dunque al pieno superamento della condizione animale. Ma, dopo quel che abbiamo visto in questo e negli altri lavori che fanno parte di The Snefru Code possiamo ancora sostenere a cuor leggero questa tesi? Al contrario, la gran massa di prove matematiche che abbiamo accumulato ci spinge a rifiutare questa visione del mondo, e ad abbandonare quindi l’evoluzionismo e il suo disprezzo per il passato dell’umanità. Per noi è venuto il momento di cominciare a prendere sul serio l’eredità che ci giunge da culture come quella Antico Egizia, e a trattarla non più come un guazzabuglio di infantili assurdità, ma invece come un prezioso patrimonio spirituale che ci consentirà di evolverci in modo ben più soddisfacente che le teorie evoluzioniste, che ci condannano a un consumismo ogni giorno più frenetico, più vuoto e disumano.

In un futuro che grazie a Dio è sempre più vicino ad essere presente, essere storici significherà riuscire a oltrepassare la misura dell’attuale visione del mondo, per assumere come nostra quella dei nostri padri, per poterla davvero comprendere. In questo modo, saremo finalmente in grado di avere una comprensione più profonda anche di noi stessi. Se non ci renderemo capaci di una tale impresa ermeneutica, avremo altrettante possibilità di scoprire il senso profondo di un posto come Giza che il classico turista mordi e fuggi, che si aggira nei paraggi per qualche ora per cercare il punto migliore per scattarsi un selfie avendo come sfondo le Piramidi.

Capitolo 15:

IL PAESAGGIO SACRO DI GIZA E IL CIRCOLO DI NABTA PLAYA: DUE ESEMPI DI MERIDIANE PRECESSIONALI DI SCALA E STILE DIVERSI CON AL CENTRO LA FIGURA DI ORIONE

1.

Assumere il punto di vista altrui, se sul momento può sconvolgere la nostra stabilità intellettuale, è un atto che però ci offre in contraccambio il dono inestimabile della chiarezza. Una chiarezza che fino ad ora, almeno per quanto riguarda l’archeologia, non si è raggiunta in pratica in nessun ambito. E qui possiamo fare un esempio di oscurità e fraintendimento, molto diffuso nell’archeologia indipendente oltre che in quella “ufficiale”, che può essere risolto identificandosi con il punto di vista altrui. A questo scopo, tratteremo un caso che ci riporta al cuore dell’argomento principale di questo lavoro. Il caso è quello delle polemiche, a volte anche piuttosto dure, che sorgono nel momento in cui le interpretazioni archeoastronomiche delle Piramidi di Robert Bauval, di Andrew Collins e di Charles Marcello vengono viste in concorrenza o addirittura in radicale contrapposizione l’una con l’altra.

Se le Piramidi rappresentano la Cintura di Orione nel 10500 a.C., così si argomenta, questo significa che non possono rappresentare la costellazione del Cigno nel 2500 a.C., e men che meno una particolare disposizione di Saturno, Venere e Mercurio. E lo stesso vale ovviamente per il caso in cui si ritenga vera la connessione con il Cigno, o quella di Saturno, Venere e Mercurio. A causa di ciò, i sostenitori delle diverse teorie fanno a gara a trovare le debolezze nella tesi che considerano avversaria non meno che a sottolineare i punti di forza della propria. Questo perché si crede tanto fermamente ch inspiegabilmente che la molteplicità delle situazioni astronomiche che il complesso architettonico di Giza e dintorni è in grado di rappresentare costituisca, chissà perché, una falsificazione del suo profondo senso astronomico. Queste persone ragionano più o meno in questo modo: con quante più configurazioni celesti il paesaggio di Giza può rappresentare, quanto più i detrattori della sua interpretazione archeoastronomica possono parlare di caso.

Ma, di nuovo, questo non è altro che un nostro pregiudizio, ancora meno giustificato di quello per cui dietro qualsiasi credenza religiosa vi debba essere per forza di cose “l’inganno del prete”. Se Giza è una meridiana precessionale che è stata pensata per segnare il 10500 e il 2500 a.C., se ha delle relazioni con Orione, Sirio, Kochab e Thuban, non si vede perché non debba essere stata pensata anche in relazione al Cigno, e poi anche a Mercurio, Venere e Saturno. Per fare un paragone che siamo in grado di comprendere benissimo, sarebbe come se qualcuno si mettesse a discutere se un certo tipo di orologio, che segna l’ora, il giorno, il mese e l’anno, sia stato fatto per segnare o l’ora, o il giorno, o il mese o l’anno. La discussione ci apparirebbe completamente assurda. Se segna l’ora, il giorno, il mese e l’anno vuol dire che è stato fatto per questo: non è che questi dati si escludono l’un l’altro. Che senso avrebbe dire che la funzione dell’orologio è ambigua, che non si sa a cosa serve, o addirittura che, se segna tutti questi dati, allora vuol dire che il suo funzionamento è dovuto al caso?

Per avere un’idea chiara della situazione di Giza, conviene andare a dare ancora un’occhiata al circolo di Nabta Playa, come abbiamo fatto altre volte in altri articoli. A quanto pare questo “circolo primitivo” immerso in un paesaggio deserto, è capace di fornire delle chiarificazioni di tipo concettuale in certi casi superiori a quelle che ci possono dare i più potenti programmi di astronomia computerizzati.

2.

Come abbiamo visto in The Snefru Code parte 6 e 8, il Circolo di Nabta Playa, oltre a essere un indicatore solstiziale, è anche una meridiana precessionale. Il suo angolo caratteristico infatti punta al solstizio d’estate, ma il suo asse principale va dal Nord a Sud. Al momento della levata eliacale al solstizio d’estate, Orione si trova lungo questo asse, e raggiunge il punto più alto nel cielo. Ma, a causa dell’oscillazione precessionale della Terra, con il passare dei millenni la sua altezza nel cielo cambia da un massimo, che nel passato più recente venne raggiunto attorno al 5000 a.C., a un minimo, che venne raggiunto attorno al 18000 a.C.

Come ben si vede dalle immagini sottostanti, il momento della massima altezza sul cielo viene sottolineato dai costruttori del circolo attraverso un aumento della scala della rappresentazione. Questo aumento delle dimensioni con l’altezza sembra il simbolo di un’idea teologica: Orione, quando è alto nel cielo, è un dio molto più potente di quando si trova in basso, sotto la costellazione precessionalmente rivale, che, come noto, è il Toro, uno dei simboli astronomici di Seth

Questa scoperta venne fatta dall’astronomo Tom Brophy, che però non si accorse di un fatto molto importante. Un semiciclo precessionale dura circa 13000 anni, mentre il circolo ne misura soltanto 16500 – 4940 = 11560. Ne mancano dunque all’appello 13000 – 11560 =1440, che corrispondono alla posizione di Orione nel punto della sua massima altezza, nel 17940 a. C. Quale potrebbe essere il motivo di questa grave lacuna, quasi impensabile, se consideriamo la perfezione a cui costantemente si protendeva lo spirito religioso e scientifico Antico Egizio?

Come prima cosa, possiamo notare che, se dividiamo la sezione del semiciclo precessionale che viene effettivamente misurata per la differenza che manca alla sua conclusione, vediamo che, sia pure in modo un po’ strano, viene fuori di nuovo la sezione aurea del semiciclo precessionale che troviamo a Giza. Infatti,

(11560 : 1440) ∙ 10³ = 8027,777.. ≈ 13000 : 1,618033.. = 8034,441..

In secondo luogo, a partire dal lavoro che abbiamo svolto precedentemente, Brophy potrebbe obbiettare che il motivo sta proprio nel fatto che 1440 è un numero molto speciale, dato che è il multiplo di 10 di un numero sacro, saturo di significati religiosi e scientifici quale il 144. Ma questo, prevedibilmente, non è tutto. Infatti, se questo particolare multiplo del 144 è stato codificato in modo raffinato, è chiaro che deve avere un’importanza particolare. Un’importanza di cui ci rendiamo conto quando scopriamo che, si colloca entro una serie di equazioni veramente impressionante, connessa con il prodotto fattoriale di numeri negativi: stiamo parlando di quella che parte dall’equazione armonica connessa con il 2, che vediamo qui sotto e che arriva infine a sfociare sia nei valori di π e ɸ che furono codificati nella Grande Piramide, sia con il 3, passando per la costante gravitazionale e la carica unitaria

x! ∙ -x! = x ∙ 10²; x = 16,010001584153..

16,010001584153..! ∙ -16,010001584153..! = 16,010001584153.. ∙ 10²

⁴√16,010001584153.. = 2,000312476..

₃inv. Ln -2,000312476.. = 3,142039.. ≈ π_Cheope = 3,142857..

Il rapporto diretto con 2 e una prima connessione con π_Cheope l’abbiamo già trovata. Ma adesso possiamo notare immediatamente che il doppio logaritmo in base 10 di 16,01.. ∙ 10² ci porta direttamente a ricavare il valore del numero caratteristico della carica unitaria, in un’approssimazione che in pratica coincide con i valori giudicati sperimentalmente corretti

log 16,010001584153.. ∙ 10²/2 = 3,204391374../2 = 1,602195.. ≈ c_u = 1,6022

Da un valore maggiore di poco più di un millesimo rispetto alla x in grado di risolvere l’equazione armonica che abbiamo visto sopra, si può ottenere la costante gravitazionale – inclusa ovviamente la potenza del 10 – attraverso un’operazione che oramai ci è diventata familiare, ovvero il prodotto fattoriale del suo valore negativo

-16,0111197.. = 6,672014.. ∙ 10^-11 = G

Applicando ora la funzione x! ∙ -x! otteniamo proprio quel multiplo di 144 che è stato codificato nel Circolo di Nabta Playa, sia pure con una leggera approssimazione

-16,0111197..! ∙ 16,0111197..! = 1440,180643.. ≈ 144 ∙ 10 = 1440

3.

Ma, come avevamo anticipato, la sequenza armonica di cui questo valore fa parte è molto più complessa di così. Possiamo rendercene conto andando a vedere il valore speculare a quello che abbiamo derivato, ovvero il valore di -G, che si può ricavare per mezzo del prodotto fattoriale di un numero negativo che non è molto lontano da quello da cui abbiamo ottenuto quello positivo

-15,125951.. ! = -6,672052.. ∙ 10^-11 = -G

In questo caso, la funzione x! ∙ -x! ci porta a una serie di simmetrie molto interessanti, fra cui anche a dei legami con i valori di π e di ɸ che furono codificati nella Grande Piramide

₂Ln [-15,125951..! ∙ -(15,125951..!)] = ₂Ln 123,285947.. = 1,571633.. ≈ π_Cheope/2 = 1,571428..

³√(16,0111197.. + 15,125951..) = ³√31,1370707.. = 3,146003858.. ≈ 2 + Ln π_Cheope = 3,145132..

[-15,125951..! ∙ -(15,125951..!)] : 10² = 123,285947.. : 10² = 1,23285.. ≈ ₂Ln (16,0111197.. + 15,125951..) =

= ₂Ln 31,1370707.. = 1,235005.. ≈ 2/ɸ_Cheope = 1,235643..

E qui possiamo concludere osservando che un’approssimazione davvero molto buona della somma dei due valori da cui abbiamo ricavato rispettivamente +G e -G la possiamo ricavare da 1/3 nel modo che vediamo qui sotto

(16,0111197.. + 15,125951..) = 31,1370707.. ≈ ₂Ln 1/3 ∙ 10¹⁵ = 31,137579013..

Forse in nessun’altra sequenza di equazioni abbiamo visto, o forse intravisto, quella che potrebbe essere la soluzione di uno dei più grossi problemi della fisica occidentale a partire da Newton: perché risulta impossibile far collimare perfettamente matematica e realtà? Da quel che abbiamo potuto constatare sopra sembra che almeno uno dei possibili motivi di questa situazione è che risulta impossibile – diciamo così – far collimare la matematica con sé stessa. Attraverso un “quasi-2” arriviamo alla carica unitaria e poi a un “quasi-π”. In qualche punto il sistema riesce a far collimare i suoi numeri fondamentali, ma in altri l’esattezza si perde. Magari per millesimi, o per decimillesimi, o anche per meno. Però si perde. Il tutto fa venire in mente una parola: indeterminazione. Quell’inevitabile inesattezza con cui il fisico atomico si scontra continuamente nelle sue ricerche empiriche potrebbe essere un riflesso di quella con cui si scontra il matematico nelle sue speculazioni astratte.

4.

A questo punto Brophy potrebbe ben sostenere che la codificazione di quel multiplo di 144 tanto importante poteva ben giustificare la costruzione del Circolo, senza bisogno di andare a scomodare altri parametri. Però a noi sembra che, anche così, la mancata delimitazione dell’altro estremo del semiciclo precessionale sia una lacuna troppo grave per poter essere accettata come una trascuratezza del progetto. E, a ben vedere, potrebbe darsi che l’interpretazione di Brophy sia incompleta. Infatti, lui sembra affascinato dall’idea che le sei pietre che si trovano attorno all’asse solstiziale del circolo segnano solo due date. Mentre a noi sembra che almeno siano tre. Basta far proseguire a Orione la sua corsa verso il basso, e ed ecco che la sua spalla sinistra e il suo collo vanno a situarsi perfettamente sulla pietra destra e centrale, mentre la sua cintura va a collocarsi sulla pietra centrale della fila di pietre sottostante. Quella che appunto rappresenta la sua cintura

Un fatto come questo sembra significare che tanto Giza come a Nabta Playa sono stati costruiti per degli scopi religiosi e astronomici molto più complessi che quello di segnare un paio di date, per quanto importanti, lungo il corso del ciclo precessionale. Il che a sua volta significa che anche le Piramidi della cosiddetta V Dinastia – Userkhaf, Sahura, Neferirkara – che rientrano piuttosto a fatica nel paesaggio sacro descritto dallo stesso Bauval, al punto che in certi casi sembrano contraddire le sue ipotesi, potrebbero avere un ruolo diverso da quello di segnare la posizione di Orione nel 10500 a.C.

Dalla prima foto sotto a sinistra si vede bene che le Piramidi di Dashour sono posizionate troppo a sinistra rispetto alla posizione che avevano le Pleiadi nel 10500 a.C. Nella foto sotto a destra, le stelle che dovrebbero far indicare la posizione della spalla sinistra e della gamba destra della costellazione si trovano a delle distanze e con degli angoli talmente sproporzionati che, semplicemente, non sembrano aver proprio nulla a che fare con quella che dovrebbe la loro posizione in un’immagine di Orione nel 10500 a.C.

Bisogna dunque che l’archeoastronomia compia uno sforzo ulteriore per comprendere quali possano essere le ulteriori date a cui alludono queste Piramidi. In particolare, sarebbe importante riuscire a comprendere il ruolo delle Piramidi di Dashour, che per la tecnica e lo stile appaiono più o meno contemporanee a quelle del Plateau di Giza. Giustificare quello che a noi sembra un errato posizionamento con delle difficoltà di tipo tecnico, è forse possibile nel caso delle Piramidi della V Dinastia, se non altro perché sono state realizzate in modo tale fa far pensare a una decadenza del sapere connesso con la costruzione delle Piramidi. Ma come poter pensare una cosa del genere in relazione a degli oggetti talmente perfetti da sfidare la precisione della nostra tecnica astronautica? Qui non possiamo fare appello a manchevolezze o a errori dei costruttori. Con ogni evidenza, siamo noi a non esser stati ancora capaci di svelare tutti gli enigmi che ci ha lasciato in eredità la scienza ermetica di ciò che noi, senza sapere cosa diciamo, chiamiamo “la Preistoria Antico Egizia”.

5.

Per altro verso, sembra del tutto chiaro che le ipotesi di Andrew Collins e di Charles Marcello, se riescono a integrare in modo meraviglioso le teorie di Bauval, non possono in nessun modo smentire la connessione del complesso di Giza, e in particolare delle tre Piramidi maggiori, con il Duat in generale e con Orione in particolare. Ci basta guardare le foto qui sotto per capire quanto invece sia intimo questo rapporto, al punto che la Piramide Rossa, la Piramide di Romboidale e, soprattutto, la Piramide di Cheope, paiono disegnate unendo con delle linee le stelle di questa parte del cielo tanto sacra per gli Antichi Egizi. Quasi che il cielo fosse per loro un puzzle, risolvendo il quale si potesse giungere alla rivelazione di quelle divine proporzioni attraverso le quali il cosmo intero è stato generato e si regge

Il Duat, e in particolare Orione dunque, sono stati assorbiti nelle proporzioni interne delle Piramidi. Al punto tale che, come abbiamo già visto in The Snefru Code parte 5, ma come conviene rivedere, potremmo immaginare di ricostruirle in modo quasi perfetto usando gli angoli di questa costellazione che, almeno su un piano geometrico-architettonico, si rivela capace di veri e propri miracoli. Cominciamo dalla Grande Piramide

Nessuna persona di buon senso può credere che tutto questo sistema di sovrapposizioni fra gli angoli e le proporzioni di Orione e gli angoli e le proporzioni della Grande Piramide possa essere attribuibile al caso. Per di più, notiamo che uno degli angoli più “usati” dagli architetti Antico Egizi per disegnare la Grande Piramide risulta proprio quello di 104 gradi, cioè quello che si trova fra la “spalla” destra della costellazione e quello che è stato interpretato come il suo braccio levato, simbolo del suo rinnovato potere e della sua resurrezione: ed è proprio alla vita eterna, alla “vita dei milioni di anni” che è mirato il culto dei monumenti Antico Egizi di ogni epoca.

Proseguendo nell’analisi degli angoli caratteristici delle altre Piramidi del Plateau troviamo che anche Khefren e Menkaure a varie riprese mostrano un intimo rapporto con gli angoli Orione. La quarta immagine di questa serie è leggermente inesatta, nel senso che rappresentando Orione in scala leggermente ridotta si vedrebbe come anche l’angolo di base della Piramide di Micerino, oltre a quello dei sotterranei, andrebbe a incastrarsi perfettamente con il fianco sinistro di Orione

Se poi ci spostiamo da Giza a Dashour troviamo che la Piramide Romboidale mostra più volte degli strettissimi rapporti con Orione. E, proprio come nel caso della Grande Piramide, vediamo che la leggera inclinazione della strada ricopia l’angolo della Cintura (l’altra piramide di Dashour, la Piramide Rossa, come vedremo fra poco, ha con Orione un rapporto meno diretto, ma non per questo meno significativo, perché i suoi angoli caratteristici sono connessi con quelli del Circolo Megalitico di Nabta Playa). Però, il caratteristico doppio angolo della Piramide Romboidale, essendo del tutto simile a quello delle tre Piramidi di Giza visto dall’alto, ha anche qualcosa a che vedere con la costellazione del Cigno

Né questo sistema di concordanze viene a mancare ove volgiamo l’attenzione al disegno del Plateau nel suo complesso. Come possiamo osservare nelle immagini sottostanti, Dashour ancor più di Giza pare seguire nella disposizione delle sue strutture un sistema fondato sugli angoli caratteristici di Orione. Questo viene dimostrato anche dal fatto che la struttura del plateau crea un sistema di “sovrapposizioni significanti” anche con la sezione delle Piramidi, le cui proporzioni, come abbiamo visto sopra, discendono direttamente da Orione e dal cielo del Duat

Anche nel disegno di altre Piramidi meno celebri di quelle di Giza e di Dashour si trovano gli angoli caratteristici di Orione: i corridoi discendenti della Piramide di Djoser, di quella di Neferirkara e di quella di Meidum trovano inesorabilmente delle corrispondenze in Orione, mentre invece nel caso Sekhemkhet – come in quello della Piramide Rossa – il rapporto con Orione lo troveremo, come si è detto, con la mediazione degli angoli caratteristici del Circolo Megalitico di Nabta Playa. Nell’ultima foto vediamo il modo perfetto con cui il diagramma dello spazio-tempo di Fappalà riesce a descrivere il ritmo dei gradoni della più “primitiva” fra le Piramidi dell’Antico Regno, la Piramide di Djoser

Osservando le immagini che vedremo fra poco, scopriremo con stupore che la presunta “comunità neolitica di pastori” che avrebbe costruito un “rozzo circolo di pietre” non solo dimostra una perfetta conoscenza del ciclo precessionale, come abbiamo visto sopra. Cosa ben più importante, i progettisti di questo raffinato segnatempo astronomico dimostrano di operare in completo accordo teologico con i costruttori di Piramidi che si credono di solito di ben tre millenni successive. Infatti, i corridoi discendenti della Piramide Rossa e di quella di Sekhemkhet ne ricopiano fedelmente l’angolo fondamentale (che è quello fra l’asse Nord-Sud e quello dell’alba al solstizio d’estate).

Inoltre, dalle immagini che seguono, scopriamo che Piramide Rossa con il suo angolo di base di 43.3° ci mostra una connessione molto interessante con quello della base del Circolo, che con il piano dell’orizzonte ne forma uno di circa 137° e con l’asse Nord-Sud uno di circa 47°. Notiamo anche che 137° risultano essere con buona approssimazione il reciproco della sezione aurea dell’angolo giro (che in realtà risulta 360/ɸ² = 137°,507764..), mentre i circa 47° corrispondono più o meno all’arco compiuto dalla Terra in metà di un ciclo precessionale^[2].

Nelle ultime immagini, possiamo vedere come il ritmo geometrico della sezione di uno degli ambienti interni della Piramide Romboidale vada a connettersi in modo perfetto con le strutture di epoche diverse della storia Antico Egizia. Questo ci dimostra ancora una volta che, se a un livello stilistico notiamo dei cambiamenti, al contrario, il codice matematico su cui l’arte e l’architettura sacra Antico Egizie si basano è rimasto identico per un numero imprecisato millenni.

6.

A conclusione delle indagini condotte in questo e negli altri lavori che lo hanno preceduto, possiamo dire che la pretesa di risolvere il significato di un paesaggio sacro come quello di Giza (ma lo stesso vale per Dashour, o Saqqara: lo stesso vale probabilmente per luoghi come Ollantaytambo, o Teotihuacan) non lo si può risolvere in modo semplicistico, attribuendogli la funzione di connettersi con una costellazione e di segnare un paio di date lungo il ciclo precessionale e arrivederci. Il lavoro di Charles Marcello e di Andrew Collins ci dimostra che non si risolve nemmeno in quei pur complicatissimi rapporti geometrici con Orione che abbiamo visto sopra, né con il suo ciclo all’orizzonte.

In un modo che appare miracoloso, ma che profondamente si connette con l’inesorabile necessità della scienza ermetica che abbiamo analizzato in questo come nei precedenti lavori, il paesaggio sacro di Giza e dintorni segna un complicato intersecarsi di cicli e tempi cosmici distinti, che vanno poi a costituire e confluire in quell’ Anno Divino, o Grande Anno, il ciclo precessionale, che era senz’altro quello più importante, il Cerchio modello e legge di tutti i cerchi cosmici.

In questo senso, l’architettura della preistoria non è diversa dal mito. Essa celebra degli dèi il cui avatar più possente sono i corpi celesti. Dunque, le loro “avventure” che si dipanano per vite millenarie, non sono altro che il riflesso dei mutamenti all’orizzonte in date topiche dell’anno umano o divino. Ed è per questo che tali “avventure” risultano connesse con numeri sacri che in un modo che forse ora non ci appare più così enigmatico emergono qua e là. Come, per esempio, quel 144 che in quel modo per noi così sorprendente è venuto fuori dall’analisi del circolo di Nabta Playa, dopo che in modi ancor più sorprendenti era venuto fuori dall’analisi della durata del periodo di Mercurio attorno al Sole o nella rivoluzione su sé stesso, o dal rapporto fra il ciclo individuato da Charles Marcello e quello di Metone, etc.

Ma, dopo quel che abbiamo visto durante questo lavoro, questo atteggiamento di reverenza verso il cielo forse non ci sembra più così enigmatico. Abbiamo visto che con gli angoli di Orione si può in pratica ricostruire tutta la produzione architettonica della IV Dinastia, ma in particolar modo la Grande Piramide. E abbiamo visto come ben tre Piramidi di questa stessa IV Dinastia si possono ricostruire come in un puzzle, semplicemente tirando delle righe che uniscono le stelle. Ma, d’altra parte, abbiamo anche visto come la Grande Piramide sembri quasi uno strumento di geometria, in grado di ricostruire l’universo dalle profondità dell’infinitamente piccolo a quelle dell’infinitamente grande. Lo abbiamo visto, ma conviene rivederlo

A questo punto la questione sorge inevitabile. Se la Piramide è uno strumento geometrico in grado di riprodurre l’universo, perché contiene in sé quelle stesse proporzioni con cui Dio lo ha formato, questo significa che le stelle del Duat, attraverso le quali si può ricostruire la Piramide, contengono in sé stesse quelle stesse proporzioni divine di cui anche la Piramide è immagine. Fu questo a quanto pare il motivo per cui nell’antichità vennero considerate sacre. Fu per questo che a Giza e dintorni si è costruito quel meraviglioso paesaggio sacro che da molte migliaia di anni, probabilmente decine di migliaia di anni, segna i passaggi dell’eterno trascorrere del tempo cosmico.

Rivediamo ancora una volta quelle quasi incredibili immagini che abbiamo visto sopra, perché mai come in questi casi, pur vedendo con gli occhi e toccando con le mani, si può credere sognare, o di sognare di star sognando. Una paesaggio stellato che contiene in sé, in modo immediato, visivo, le proporzioni geometriche e matematiche della Mente Divina, quasi un volto divino che mentre lo guardiamo ci guarda. O un’immagine della Mente Divina, che mentre la pensiamo è il nostro stesso pensare, è il nostro stesso pensiero. Chi avrebbe mai osato immaginare che un giorno questa che sembra una follia filosofica potesse trasformarsi in visibile realtà?

7.

Si vorrebbe gridare al miracolo. Noi sappiamo che queste stelle non sono appoggiate su un piano, e nemmeno sulla superficie interna di una sfera. Sono disperse in uno spazio umanamente inconcepibile. Alcune sono lontane più di mille anni luce, altre sono relativamente vicine: solo se viste dalla Terra compongono quelle meravigliose immagini che finiamo ora di vedere. Che cosa può voler dire una cosa del genere? Inesorabilmente viene alla mente il Salmo 18

I cieli narrano la gloria di Dio,
l’opera delle sue mani annuncia il firmamento.
Il giorno al giorno ne affida il racconto
e la notte alla notte ne trasmette notizia.

Senza linguaggio, senza parole,
senza che si oda la loro voce,
per tutta la terra si diffonde il loro annuncio
e ai confini del mondo il loro messaggio.

Là pose una tenda per il sole
che esce come sposo dalla stanza nuziale:
esulta come un prode che percorre la via.

Sorge da un estremo del cielo
e la sua orbita raggiunge l’altro estremo:
nulla si sottrae al suo calore.

In effetti, parlare di caso in situazioni del genere sembra una stupidaggine che sorpassa qualsiasi superlativo. Dunque dobbiamo parlare di Dio. Dio ha voluto che dalla Terra, contemplando il cielo del Duat, si potesse in questo modo contemplare il segreto splendore dell’Intelligenza con cui ha formato il cosmo. Cos’è allora il Duat, è un’immagine stellare del Paradiso Terrestre? o di quello futuro che attende i Beati? Cosa ci vuole insegnare quest’immagine: che per conoscere la vera gioia occorre distogliere gli occhi dal mondo che ci circonda e guardare, come si dice, in alto?

Ma noi sappiamo che, dal punto di vista scientifico, non esiste né alto né basso. Il cosmo, come insegnava Ermete Trismegisto, inconsapevolmente riscoperto da Einstein, è un’infinita sfera, il cui centro è ovunque e la cui superficie è da nessuna parte. Dunque nemmeno Orione e il Duat sono “in alto”, se non in modo del tutto relativo e dunque, in ultima analisi, illusorio.

Quindi Dio forse ci vuol dire che anche l’altezza delle stelle è un’altezza illusoria, che l’altezza cui dobbiamo volgerci è interiore, invisibile, puramente spirituale? Oppure che in quest’universo, dove lo spazio sembra cartesianamente ovunque uguale, vi sono eppure dei luoghi in cui il sacro si manifesta in modo più profondo che altrove?

Ci si domanda se esistano in altri mondi altri cieli in cui si può contemplare una proporzione del genere, oppure se la Terra è un centro spirituale da cui la Mente Divina può essere contemplata in modo più perfetto che da qualsiasi altro punto dell’universo. Questo restituirebbe alla Terra quell’unicità che con la rivoluzione di Copernico avrebbe solo apparentemente perduto. Dunque il Duat e Orione sono un’immagine di Dio tanto perfetta da parafrasare astronomicamente la frase evangelica “Chi vede me vede il Padre”?

8.

La modernità venuta assieme a quella che è stata chiamata “la perdita del centro”. Ancora fino al tempo di Galileo – così credevamo – in Occidente come in tutto il mondo si è creduto che la Terra fosse al centro dell’universo creato da Dio, e che l’uomo fosse al centro della Creazione. Solo così l’uomo ha potuto pensare che la sua esistenza finita e casuale potesse avere un senso eterno. Ma l’entrata in scena del metodo scientifico ha ben presto retrocesso queste concezioni metafisiche al rango di fiabe della nonna. Le stelle della galassia sono come i granelli di sabbia del deserto? Ben presto scopriamo che la galassia non è altro che un granello di sabbia perso in un deserto di ammassi di galassie, il mare dello spazio notturno non è che una goccia nel mare. Troviamo scritto a questo proposito nell’introduzione a Il Mulino di Amleto

Einstein ha detto: «Ciò che è inconcepibile, dell’universo, è che esso sia concepibile». L’uomo non si arrende. Quando scopre milioni e milioni di remote galassie, e poi le radiosorgenti quasistellari distanti miliardi di anni luce che sopraffanno la sua mente, egli è felice di poter attingere a simili profondità. Ma paga un prezzo terribile per i suoi successi. La scienza dell’astrofisica si protende su ordini di grandezza sempre più vasti senza perdere il proprio punto d’appoggio; all’uomo in quanto tale ciò non è possibile: nelle profondità dello spazio egli perde se stesso e ogni senso della propria importanza. Collocarsi entro i concetti dell’odierna astrofisica gli è impossibile, se non nella schizofrenia. L’uomo moderno sta affrontando il non-concepibile; l’uomo arcaico invece manteneva una salda presa sul concepibile, inquadrando nel proprio cosmo un ordine temporale e un’escatologia che avevano un senso per lui e riservavano un destino per la sua anima.

G. de Santillana – H. von Dechend, Il Mulino di Amleto, Adelphi, p. 25

Per una volta, troviamo in questo testo tanto controcorrente con la modernità, qualcosa che più o meno tutti gli intellettuali moderni avranno facilmente e spontaneamente condiviso. La contrapposizione uomo antico – uomo moderno, con l’uomo antico saldamente legato a un mondo antropocentrico, e un uomo moderno scagliato nello spazio caotico di un universo che si dilata a partire da un’inspiegabile esplosione originaria e in un tempo smisurato che tende al proprio annientamento. L’uomo antico ha potuto credere nel senso del proprio vivere solo a partire dall’ignoranza del metodo scientifico: una volta che alla sua ignoranza è stato posto rimedio per mezzo del metodo scientifico, è cominciato il male senza rimedio dell’uomo padrone della scienza, essere senza oramai altro destino che l’angosciata o sarcastica contemplazione del proprio stesso nulla.

9.

Ma il lavoro che abbiamo fin qui svolto sembra dimostrarci che questo che credevamo l’estremo punto d’arrivo della condizione umana, la piena e perfetta conoscenza dell’insensatezza del cosmo e perciò della vita e della storia umana non è altro che un’illusione. Quegli spazi cosmici, fatti di sistemi solari che credevamo caotici sono regolati secondo leggi armoniche che li rendono un tutt’uno con quel minuscolo sistema solare che possiamo vedere nell’atomo. La struttura dell’intero universo infatti pare fondarsi su numeri – π, ɸ, il 10 e il numero di Eulero – che lungi dal derivare da una casualità di tipo empirico, derivano dalla matematica e dalla geometria più astratte che si possono immaginare. Il cosmo è dunque fatto a immagine di un misterioso Creatore, che l’ha fatto specchio dell’ordine matematico che è la sua mente stessa.

In sintonia con ciò, il mondo dei numeri, lungi dall’essere il frutto di un ammasso informe di tecniche di calcolo, si è rivelato alla nostra analisi come una distribuzione ordinata di entità che possiamo paragonare ai neuroni del cervello umano. Solo in apparenza essi sono dei punti su un asse cartesiano, che si differenziano dagli altri esclusivamente per la posizione che occupano in una successione informe. Al contrario, essi si sono rivelati delle complesse entità organiche, strutturate in una meravigliosa molteplicità di rapporti, si che possiamo del tutto legittimamente ipotizzare che alcuni di essi abbiamo delle potenzialità molto maggiori di altri di simbolizzare la totalità a cui appartengono. In questo senso, abbiamo dimostrato che le misure del lato e dell’altezza della Piramide, o la durata dell’anno solare e di quello delle fasi lunari, non rappresentano soltanto delle proporzioni astratte. Al contrario, essi si costituiscono al loro interno e nei rapporti strutturali con la cifra complementare un sistema organico di proporzioni armoniche che nell’analisi si è svelato tanto meraviglioso quanto o più di una musica di Bach.

Da ultimo ci troviamo nella meraviglia delle meraviglie, nel sancta sanctorum di questo tempio smisurato che è l’universo: il cielo di Orione, il cielo del Duat, che contiene in sé l’immagine della Mente Divina, che sulla Terra l’uomo ha riprodotto nelle proporzioni della Grande Piramide.

Dunque non è vero che l’uomo antico ha potuto dare un senso all’universo e credere in un destino eterno della propria anima solo a causa della sua ignoranza, e che a causa del nostro sapere noi, uomini moderni, l’abbiamo perso. Le cose stanno in modo diametralmente opposto. L’uomo antico vedeva un senso nel cosmo e vaticinava un destino eterno per la sua anima a causa di una sapienza ermetica che, perdendosi, ha lasciato gli uomini dapprima nell’ignoranza scientifica, e poi nell’incredulità religiosa. Con la distruzione delle ultime tradizioni orali Antico Egizie, voluta dall’imperatore Teodosio, che fece del Cristianesimo la fede unica e obbligatoria dell’Impero Romano, il maestoso fiume del sapere divino, già diventato un misero rivolo, si è trasformato in un letto che sembrava per sempre disseccato.

10.

Ma ora questo dramma millenario è giunto finalmente alla sua conclusione. Attraverso lo studio delle proporzioni della Grande Piramide, o di libri come i Veda o il Pentateuco, l’uomo moderno può tentare di ricongiungersi con la scienza dell’uomo antico. La Sapienza dell’Età dell’Oro non è più un mito, una ninna per bambini: è oramai una materia di studio aperta a matematici e scienziati disposti a fare della matematica il cuore della loro conoscenza. Orizzonti smisurati si aprono anche per il nostro sapere storico, filologico, archeologico, e perfino paleontologico, per non parlare delle possibili implicazioni tecniche connesse con lo sfruttamento di forme illimitate di energia pulita, che la teoria dei campi unificati che fu codificata nella Grande Piramide rende immaginabili, se non ancora possibili. Il nostro mondo rischia l’Olocausto nucleare a causa della lotta spietata per materie prime sempre più scarse e sempre più indispensabili, il mondo umano e naturale rischia di annegare nel mare di rifiuti prodotto dal consumismo e dal capitalismo: ma la sapienza antica ci viene oggi in soccorso, e ci dà la possibilità, se non ancora di sperare, di immaginare una speranza, tanto per il corpo dell’uomo che per il suo spirito.

Infatti, da oggi volgersi alla scienze umanistiche diventa lo stesso che rivolgersi allo studio della matematica e della fisica più astratta, come volgersi allo studio della fisica e della matematica più astratta è come volgersi allo studio della musica. Il divino ritorna a essere l’orizzonte e il fondamento del sapere umano. Nei ritmi musicali di una poesia potremo simbolicamente ascoltare il crescere degli orbitali dell’atomo, o l’avvolgersi delle galassie su sé stesse. E sempre e ovunque possiamo ritrovare il misterioso volto del Creatore, nella teologia, come nei rami più specialistici della chimica, o nei più aridi meandri della logica.

Certo, se tutto questo è vero, possiamo e anzi dobbiamo domandarci: perché Dio ha permesso il verificarsi di una tragedia tanto immane, come la perdita della conoscenza perfetta del cosmo, che fu senz’altro un suo dono originario all’uomo? Perché questa finestra sull’Altrove è stata per secoli sbarrata dall’ignoranza, dalla cecità, perché il sapere che ha permesso la costruzione delle Piramidi è stato dimenticato e solo ora su di esso si apre uno spiraglio? Perché per secoli Dio avrebbe permesso che ci trascinassimo in dubbi angosciosi, che alla fine del millennio scorso si sono trasformati in molte menti nella certezza che l’universo non sia altro che un prodotto del Caos?

Lo confessiamo apertamente: noi non abbiamo nemmeno un lacerto di risposta a questo domandare, tanto più drammatico quanto più grande è la gioia di questa riscoperta. L’unica cosa che sembra chiara è che la sola possibilità di sapere qualcosa di più quanto al senso degli ultimi secoli dell’umanità, davvero un’Età del Ferro se confrontata con la luminosità della sapienza che possiamo intravedere attraverso il lavoro che abbiamo svolto, sta nello studio approfondito di quei resti che di sé ci ha lasciato quell’Età dell’Oro a cui senza saperlo ci protendevamo con i nostri sforzi. Un’eredità molto meno misera e molto meno criptica di quanto fino a oggi potevamo immaginare.

PENELOPE

Je ne puis plus, baigné de vos langueurs, oh lames,
Enlever leur sillage aux porteurs de cotons,
Ni traverser l’orgueil des drapeaux et des flammes,
Ni nager sous les yeux horribles des pontons.

A. Rimbaud

Itaca lontana, dalle torri d’argento.

Itaca cantata, nel tramonto silente,

Foglia su cui galleggia la corrente,

Infante di sogni in braccio al tempo.

Itaca alata, salata, del dolore:

Cuore di pietra, rifranto come l’onda,

Mare senza tempo, senza sponda,

Ebbra e perduta fragranza dell’amore,

Confuso com’è confuso ogni ricordo.

Oh diafana sera, oh morte in cui non credi,

Il canto che odi non conosce accordo

Se ciò che fu orizzonte è suolo indietro i piedi,

Se il viaggio finisce nel suo dissolto incanto:

Solo mi brucia il fatuo inferno del rimpianto.

ODE IN MEMORIA DI..

Appoggiata al balcone che sul ciglio dell’orizzonte ti sospende, la mano levata come in un saluto che staccarsi non può dall’ultima eco di quell’ «Addio!» impronunciabile, che come l’onda sul mare da te mi separa e in te mi getta, sospeso come il viola scuro nelle bianche nubi che sull’ultimo verdognolo e giallino tremare del tramonto, fra schiume di accecanti brine che si perdono in una bruma d’oscurità di cui nulla so dire se non «..di cui nulla so dire.. ».

Tu hai impugnato lo scettro e pronunciato l’incantesimo.

Il bardo cieco e muto muove le labbra, imitando i movimenti che la sua bocca farebbe se pronunciasse quella strofa antica, che accompagna accarezzando dolcemente le corde del suo liuto senza corde. Il teatro tutto lo ammira rispettando un silenzio senza fondo, perché la pantomima risale ad abissi di tempo di cui nessuno osa o può pronunciare la vertigine. Così, nessuno comprende quel che accade, questa è la Verità. Ma se l’esecuzione rispetta il rigido cerimoniale e le perfette proporzioni tramandate dal mito, l’applauso sarà tanto fragoroso che il tetto e le mura crolleranno sul bardo muto, sul palco per il resto vuoto e sugli spettatori, che nulla sanno di nulla, forse nemmeno che quella a cui hanno assistito è una pantomima.

Tu hai impugnato lo scettro e pronunciato l’incantesimo.

Il mare è ormai privo di velluto. Le teste tagliate in omaggio al centro che eterno si avvita su sé stesso affogano nell’abisso del loro stesso interminabile dissanguarsi. Oh, la vita, miracolo fra i miracoli! Non vedi che come il sangue mai, mai non cessa di sgorgare?

Tu hai impugnato lo scettro e pronunciato l’incantesimo.

Il vassoio d’argento è indistinguibile dalla fonte cristallina di questo specchio in cui la mia angoscia e il mio lamento si riflettono inutilmente. Già sono cieco: già non vedo i tuoi più nei miei occhi.

Tu hai impugnato lo scettro e pronunciato l’incantesimo.

Io sono fra coloro che si impigliano in inutili sillogismi, nei vuoti sarcasmi del tempo. Un’eternità è passata, eppure eccomi qui, inginocchiato, ad ascoltare il cielo vuoto e ancora vuoto del ricordo.

QUANDO

Nadie hubo en él; detrás de su rostro (que aun a través de las malas pinturas de la época no se parece a ningún otro) y de sus palabras, que eran copiosas, fantásticas y agitadas, no había más que un poco de frío, un sueño no soñado por alguien.

J. L. Borges

Quando morirà “io”, non morirà nessuno, o morirà, forse,

Quel qualcuno che non sono mai stato. Una muta presenza

Svanirà dagli occhi muti e vuoti, nel vuoto specchio,

E muto, del mattino, e una muta assenza, la mia presenza,

Nel vuoto specchio, e muto, di altrui occhi. Vecchio,

Forse, vittima del tempo inesorabile, o, chissà, forse

Della mia stessa non più incerta mano, forte di una risoluzione

Che dimenticò ogni dubbio, che ogni morso, rimorso,

E ogni rancore si lasciò alle spalle, infine, per abbracciare

Quel nulla che nell’oblio ci promette la fine del percorso

Di illusioni aspre e deluse, e di memorie vaghe e amare.

Così giungerà la da sempre e invano cercata rivelazione:

Saprò finalmente chi è colui che si domanda “io chi sono?”,

Chi da sempre mi cerca, mentre io da sempre non ci sono.

VARIAZIONE

Esiste una stanchezza dell’intelligenza astratta ed è la più terribile delle stanchezze. Non è pesante come la stanchezza del corpo, e non è inquieta come la stanchezza dell’emozione. È un peso della consapevolezza del mondo, una impossibilità di respirare con l’anima.

Fernando Pessoa

La vita io l’ho vissuta

vivendola.

Fin dove il cuore mi resse

continuò a battere.

Ora la mia giornata non è altro più

che quel ch’è sempre stata:

uno sterile affaccendarsi

di ottuse e stupide abitudini,

inutile fra tutte quella di evadere, si,

dal vecchio cerchio,

solo per trovarmi poi rinchiuso

in quello che subito lo chiude,

più nero e stretto del primo

da cui naturalmente, lo so,

non sono mai fuggito.

Così, quando all’alba insonne mi riduco

una frenesia di morte omicida mi conduce,

estro esasperato, immortalità bramata

che per non morire smania

di non mai e mai più:

mai più dormire!

E andando avanti, fra mille luci allucinate sogno

partenze immobili, lontananze friabili,

lotte risibili contro angeli fugaci,

speranze sempre più vuote e labili

di liberazioni ultime

e impossibili.

Oimè. Tutto il mio chiuso

e cocente sospirare

altro sfogo non ha

fuori che il sonno che non viene!

Invano, invano lotto

per possedere i giorni

che mi travolgono,

ombre mutevoli,

incubi numerosi.

Io nego,

mi lego,

annego nel tempo.

A UN BACIO VISTO PER STRADA

Tiene la mano sulla guancia dell’amato, sole che sorge sullo spalancato orizzonte delle sue palpebre socchiuse, e dalle sue labbra sugge un fiato come il latte dolce, che dal seno materno nella fame dell’infante scorra.

Beata inconsapevole! Pensi il non pensare, e in questo mare salpi, vaghi e poi ti perdi, come nel fresco della brezza il sospirare: splendida adolescente, ama quel tuo compagno che come boccio di rosa coperto di rugiada nelle tue mani tremule si schiude, là, dove gli amanti il Dio che li commuove con le ali dell’amato li solleva!

Amore: che altro cerchiamo infine, che altro mai e poi mai si può trovare?

Amore mio ascolta: per mezzo di colei che nel baciare serrato si disperde, nel chiuso dei miei occhi ti rivedo.

Amore, tu lo sai, io sono qui per vivere, non per sognare. Così non sorrido e non m’illudo. Io so che le tue rime – cuore, fiore, colore, sapore – intrise sono e scorrono nel duro metro, nella morsa del Tempo e del dolore. Lo so, lo so bene, ma di queste parole eppure non mi pento: che importa infine se il rosso delle tue rose in corona di spine si ritorce? Il tuo dolce fiorire un giorno, nel giorno del morire, vincerà la morte.

INTERLUDIO

Varsavia.

Varsavia coperta di neve

e d’invisibili fiori

che dei biancori illimitati

della neve si nutrono

e risplendono

meravigliati.

Varsavia del ghetto,

della strage.

Varsavia mille volte rasa al suolo

e mille volte

come me

risorta.

Varsavia tua patria,

tuo cielo. Varsavia nei tuoi occhi

nel mio amore

come un velo.

Varsavia del tuo riso d’argento

e di quell’intimo pianto

di cui più non mi curo

che quasi più non sento.

Varsavia dei passi che rimbombano

nel silenzio di spettri di una via laterale,

di una vita qualsiasi che passa

affranta di tristezza

e di cui nessuno poi

saprà più nulla.

Varsavia..

Varsavia che si allontana

come una valle in un’evanescenza

di nebbie senza meta,

labirinto irreale per cui si smarrisce

il cuore

mentre cerca senza posa quel che resta

di un suo perduto e splendido

dolore.

Varsavia, lo so,

ormai quasi soltanto un nome

che nel tenue sfumarsi nella memoria

si sfuma e s’attenua

come il tuo viso

in una penombra di pergola in estate,

fissando un angolo oscuro

là dove vorrei ci fossero

i tuoi occhi.

TANGO A VARSAVIA

a S.

Varsavia, 3 aprile 2011, Zlota Milonga

Ah ! les haillons pourris, le pain trempé de pluie, l’ivresse,

les mille amours qui m’ont crucifié !

A. Rimbaud

1.

Cielo di notturno silenzio dei tuoi occhi, sopito fuoco

Fra lacrime d’ebbrezza, fiorito e dolce stupore del sorriso,

Giglio sensuale come il loto, insidia che fa il respiro roco,

Sull’onda che carezza il torso, il collo che ripido e deciso

Sale al morso di miele delle labbra, alla lingua di rosa

Di fragola e ciliegia, al dente di levigato avorio che porto inciso

Qui, nel mio cuore che duole se ti vedo, o se ti sogno, penosa

Tenerezza, male che si dibatte quando ci sei, o se manchi,

Perché Altrove è sempre il luogo dell’amore, e dolorosa

La gioia degli amanti. Così, ecco il freddo rogo degli stanchi

Versi, ecco queste parole, vuote e tristi come un commiato,

Ecco il tocco tenue e stremato della nostalgia, ecco i suoi bianchi

Doni, ecco un’immagine che lascia senza mani, senza fiato,

Ecco un tuo gesto fatto di brezza, ridente, struggente, come alato.

2.

Velo di seta in ebbrezza la tua pelle, volo di seta su seta

La tua gonna, che avvolge e svolge la luna piena del sorriso,

Vita che si avvita nel mistico caos del sangue, alta cometa

E dolce, nell’aspra malattia del tango. Astri inondano il tuo viso,

La lenta e tentante carezza dei tuoi passi, che lievi

Tornano e vanno, tenue risacca, brezza, mare d’altro mare intriso,

Farfalla che su farfalla si posa e prende il volo. Levi

Un istante la testa, nel sigillato abbraccio dell’amante

Nascosta e offerta come biancore di perla nelle brevi

E socchiuse oscurità dell’intima conchiglia, e in un istante

Di nuovo la sprofondi. E come il delfino l’arco teso del salto

Ridona al vago vortice dell’onda, così una nota tremula e distante

Ti ridona all’abisso, al gorgo di seta dei tuoi giri, alto

Come il cielo quando dopo la pioggia il sole ne fa smalto.

3.

Incanto, dove si cela il dio del tuo tormento nel tutto o nella parte?

Così, di dove inizia a far male tua grazia, dalla tumida brocca,

Ardente, della bocca, dal rosso suo denso, intenso, accesso d’arte

Che strazia l’anima con estasi d’incenso? Oppure che scocca

La suadente freccia è la luna d’oriente sulle labbra, l’insinuante

E curvo mutare del sorriso, biancore pazzo d’avorio che la rocca

Salda e acuta dei denti dissolve in una luce? E cosa ama l’amante

Di te, il diafano velluto della pelle, la giunzione ammiccante

Della vita con i fianchi, o il passo rotondo, elastico, ondeggiante?

Oppure è la tua voce roca che dal fondo dell’anima vibrante

Il filo delle tue forme avvolge e svolge in sensi di frusciante

Seta, e che velando e svelando fa di parti ottuse il tutto lancinante?

Io non so dire di più, se non che tu sei bella, nostalgia danzante

Di patria che ho perduto, seno di sole che s’offre dal levante,

Armonia stupenda, che quanto più vicina sei distante.

4.

Volerti afferrare, volerti stringere, o toccare, o anche solo

Sfiorare, è volerti perdere, ultima sete e luce di speranza,

Ultima stanchezza, ultima passione, che forse non sei che il volo

Labile di un sogno, vaghezza d’un pensiero che nella vana danza

Dei giorni m’accompagna perché all’inganno lieve del suo velo

Si celi questo deserto fatto di vento e tempo che si avanza

Inesorabile a quel nulla che senza vedere eppure vedo

Come sola eternità e solo essere a cui la vuota vita umana

Nel suo breve sussulto si protenda. Così, solo sognando ti cedo

Tenerezza, e solo con passi di sconsolata, grigia e quotidiana

Nostalgia ti seguo nel tuo andare non so dove, stonato aedo

Che questa sorda ballata affida al vento, al caso, alla strana

Divulgazione del fato perché ti giunga, fato in cui non credo,

Caso in cui non spero, vento che non amo, cui più mi nego

Più mi lego.

LE TUE VALIGIE

Jamais l’espérance,

Pas d’orietur.

Science et patience,

Le supplice est sûr.

A. Rimbaud

La tua leggerezza, le tue valigie, il tuo partire, come li invidio!

E so di essere pazzo. Perché l’invidia

è sempre una cosa da pazzi.

Alla fine, cosa c’è da invidiare a questo mondo?

Solo l’aria, l’acqua e il pane e il resto

– tutto il resto – sono fole al vento.

Lo so benissimo questo, e lo ripeto.

Eppure ti invidio lo stesso.

La tua leggerezza, le tue valigie, il tuo partire, come li ammiro!

Li vedo andare sulla superficie inutile del tempo

come un magico pesce volante che vagamente rimbalza sulle onde,

da te benedette ora qui, ora là, poi chissà dove!

Non riesco a credere o a pensare

che siano quelle lì le tue catene,

la tua zavorra, il tuo tormento,

il tuo destinato esilio da te stessa,

come lo è per me stesso il rimanere qui,

dove non sono.

PARIGI (PRIMA DI TE E DOPO DI TE)

Si je désire une eau d’Europe, c’est la flache

Noire et froide où vers le crépuscule embaumé

Un enfant accroupi plein de tristesse, lâche

Un bateau frêle comme un papillon de mai.

A. Rimbaud

I.

PARIGI DOPO

Strade larghe come piazze,

piazze smisurate come il deserto

eppure piene di gente che va e viene. Parole

colte al volo qua e là,

fra i rumori del mondo e di “tout le monde”,

in una lingua nel cui suono echeggia continuamente

un nome: Arthur Rimbaud.

Poi:

musei che erigono un mistico, fantastico e proteiforme labirinto,

cattedrali ebbre di simboli che sfidano l’abisso,

lontani orizzonti normanni d’acciaio, di torri e cavalcate,

le barricate, gli incendi, le canzoni, le grida interminabili

della Rivoluzione, Napoleone, la Senna che scorre

lenta e veloce come il tempo e poi…

Poi?

Poi

tante, troppe, quasi infinite cose,

che nella memoria confusa e sterminata sfuggono

come luci scagliate via da un treno in corsa:

le nazioni, le esplorazioni, le colonie, gli imperi,

i popoli, i populismi, l’individuo, gli individualismi

la tecnica, la scienza, il progresso, la repubblica,

le democrazie, la Prima Guerra Mondiale,

il dopoguerra, il comunismo, il fascismo,

l’esistenza, l’esistenzialismo, la crisi del ’29, il nazismo,

un’altra Guerra Mondiale ancora,

ancora un altro dopoguerra,

la ricostruzione, la guerra fredda,

lo sviluppo, il Maggio,

i giovani del Maggio,

il flusso e il riflusso

e poi…

…poi…

Poi

perché lottare

per ricordare qualcos’altro

ancora?

Qui

puoi trovare davvero di tutto

e dappertutto

così che non c’è mai niente infine

da cercare.

* *

Lontana

la Tour Eiffel si sfuma

come dietro una finestra

su cui il fiato taciturno allarga un velo:

sono le lacrime al pensiero

che per anni e anni

proprio tu

hai visto questo cielo.

II.

Moi qui tremblais, sentant geindre à cinquante lieues
Le rut des Béhémots et les Maelstroms épais,
Fileur éternel des immobilités bleues,
Je regrette l’Europe aux anciens parapets !

A. Rimbaud

PARIGI PRIMA

Il

cielo….

Il cielo come

cieco,

come

in eco…

Quel cielo

lontano,

andato via

e così…

…perso,

come disperso

nel deserto di pietra

avita,

senza vita

dell’inverno.

Un sorriso intristito,

impaurito

solca l’aria tetra.

Rigida,

rattrappita

nella carezza gelida

del vento,

la fronte china

sotto quel cielo basso,

in quella pioggia lenta,

troppo lenta,

troppo fine

per poterla chiamar pioggia

e troppo spessa

per poter credere vero quel portento

– sentirsi perduto nella nebbia –

in cui eppure follemente crede.

Labili schegge

di sabbia scura: ecco

la dura Senna

dove come gabbiani all’orizzonte

si perdono

le voci e i palpiti

dei bianchi vaporetti,

che straripano di gente

che gli pare allegra.

Passeggia lentamente

carezzando dolcemente

i parapetti.

Immerso nel segreto

del suo interno silenzio,

immenso,

non ode i rumori:

dappertutto c’è gente

e non vede nessuno.

Distratto da ricordi che non sa di avere

l’adolescente timido balbetta frasi dal significato incerto

in quella lingua nasale che l’infante iniziò forse a imparare

e che l’adulto finirà poi per dimenticare

quasi del tutto.

I marmi impassibili,

Notre Dame

impossibile.

Un volto che sa di non conoscere

e che pure crede di riconoscere

svanisce dietro un angolo,

mentre come in preda alla febbre percorre

i vasti labirinti del Louvre,

dove alla fine ogni corridoio

si biforca in epoche perdute, simboli incomprensibili,

dèi e fedi surreali,

abissi di eventi e tempo che si sciolgono

poi

fra i labirinti del traffico, fra le strade gigantesche

di cui quasi non riesce ad immaginarsi

l’immane traversata,

gli occhi sperduti sulla vetrina oscurata in cui

il suo vano riflesso scruta quello

ancor più vano,

ancor più inumano

della Tour Eiffel

che si arrampica verso quel cielo

oramai così

lontano e così….

….così perso,

come disperso

nel deserto di pietra

avita,

senza vita

dell’inverno.

Una stagione all’inferno

finiva

un’altra ne iniziava

interminabilmente.

Fumavo Gauloises, bevevo cognac,

credevo di cercare un altro Altrove

– disperatamente –

e invece come un eroe

stanco e di un altro evo

stavo tornando a casa

e non lo sapevo.

1. Per chi non avesse letto i lavori precedenti, una potenza-specchio sarebbe un numero elevato alla potenza di sé stesso, cioè la funzione x^x, che noi simbolizziamo con x^S: in questo caso 3/ɸ^3/ɸ = 1,854101..^1,854101.. = 1,854101..^S = 3,141572.. ≈ π = 3,141592.. ↑
2. Sui rapporti fra sezione aurea, ciclo precessionale e arte ed architettura sacre Antico Egizie si veda The Snefru Code parte 4 IL NUMERO D’ORO NELL’ARTE E NELL’ARCHITETTURA SACRA ANTICO EGIZIA: UNA PROSPETTIVA ARCHEOASTRONOMICA ↑