LA THÉORIE DE LA RELATIVITÉ DANS L’ESPACE ARCHITECTONIQUE ET FIGURATIF SACRES DE L’ANCIENNE ÉGYPTE ET DANS LE TIMÉE DE PLATON
(AVEC UNE ESQUISSE DE LA THÉORIE DES CHAMPS UNIFIES PROBABLEMENT CODÉE DANS LA GRANDE PYRAMIDE, ET UNE ANNEXE SUR LES POSSIBLES RELATIONS NUMEROLOGIQUES ENTRE LE SYSTEME CALENDRIER MAYA HAAB’ – TZOLKIN AVEC CETTE THÉORIE)
À Ermanno,
mon oncle et mon premier maître de philosophie
Donc tu te dégages
des humains suffrages,
des communs élans !
Tu voles selon…
A. Rimbaud
partie première: LA THÉORIE DE LA RELATIVITÉ DANS L’ESPACE ARCHITECTURAL ET FIGURATIF DE L’ANCIEN ÉGYPTE
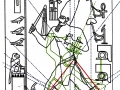
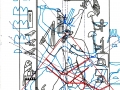
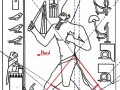
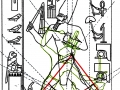
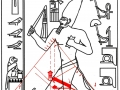
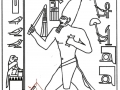
1. Dans les deux articles précédents – Hypothèse de lecture de la stèle de Snéfrou et Les stèles de l’Ancienne Égypte : premières considérations historique-symboliques et nouvelles découvertes géométriques – de l’analyse géométrique de la stèle de Snéfrou et d’autres œuvres bien connues d’époques et Dynasties différentes semblait résulter d’une façon assez claire l’existence d’un code géométrique commun qui pouvait relier l’architecture et l’iconographie de la culture sacrée de l’Ancienne Égypte à travers les millénaires. Le phénomène géométrique identifié comme premier était celui qui se définit comme un système de « intersections signifiantes » entre la stèle de Snéfrou et les Pyramides de la IV Dynastie, un système qui sans doute semblait faire allusion à un code qui l’avait géométriquement généré. Le prochain pas de la recherche nous a conduit à émettre l’hypothèse que ce code devait certainement être basé sur la section d’or, même si nous n’avons pas approfondi le problème au point de faire de conjectures positives quant à la méthode par laquelle cet « espace d’or » avait été établi et utilisé. Mais il suffirait de faire quelque pas de plus en avant dans la recherche pour arriver au point d’avoir à disposition une hypothèse concrète et croyable pour la solution de cet épineux problème. Une solution qui – en dépit d’être tout à fait inattendue et quelque peu incroyable – peut-être à la fin de cette exposition vas résulter, au moins dans un certain sens, moins « impossible » de ce qui semblait qu’on pouvait supposer par principe. Nous étions déjà conscients que la Grande Pyramide et beaucoup d’autres monuments de l’Ancienne Égypte supposaient une technique beaucoup évoluée : mais une technique beaucoup évoluée suppose à son tour des connaissances scientifiques et mathématiques également évoluées, et en ce sens les hypothèses que nous allons exposer en cet article sont en pleine continuité logique avec les résultats des enquêtes métrologiques et scientifiques que l’on a fait sur ces chefs-d’œuvre de l’art et de l’architecture préhistorique. 2. L’analyse computérisée d’une stèle qui est devenue célèbre avec le nom « Djoser running » – et dans laquelle on avait déjà noté dans l’article « Les stèles de l’Ancienne Égypte : premières considérations… » quelques exemples très significatifs de rapports d’or entre les parties constituantes1 – a donné un résultat assez intéressant, car on a constaté que le rapport entre la largeur et la hauteur de la stèle est plus ou moins égal au Nombre d’Or (1,617 calculés sur l’image, contre 1,618 du Nombre d’Or). Donc on a pu observer spontanément qu’un espace comme celui-ci – qui quelles que soient ses dimensions réelles préserve des qualités géométriques liées au Nombre d’Or (et donc aussi à la section d’or) –se prête à son tour à être divisé en parties qui conservent, probablement de façon même assez compliquée, un tel rapport. Pour comprendre la raison de notre choix, il faudra peut-être une brève description de la structure géométrique de ce merveilleux phénomène naturelle, l’inflorescence du tournesol. Les enquêtes statistiques nous disent que dans la nature, dans le cas le plus fréquent, il y a 34 spirales logarithmiques enroulées dans un sens et 55 dans le sens inverse,2 c’est-à-dire selon le couple de la série de Fibonacci, qui est aussi à la base de la proportion des spirales elles-mêmes. Dans le cas de tournesols supérieurs à la moyenne on voit que, si on procède du centre de l’inflorescence vers la périphérie, le rapport ne reste pas constant, mais passe d’un couple quel que soit de nombres de Fibonacci contigus au couple successif (ainsi, si le premier rapport était 55/34, le second sera 89/55). Nous pouvons observer deux modèles typiques de l’inflorescence du tournesol dans les images ci-dessous
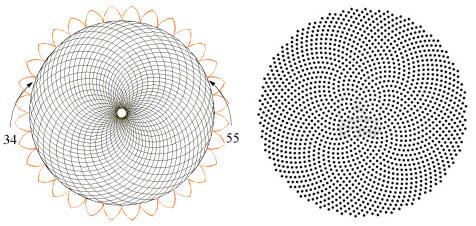
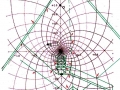
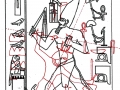
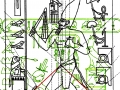
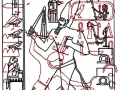
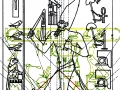
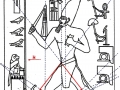
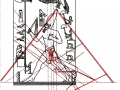
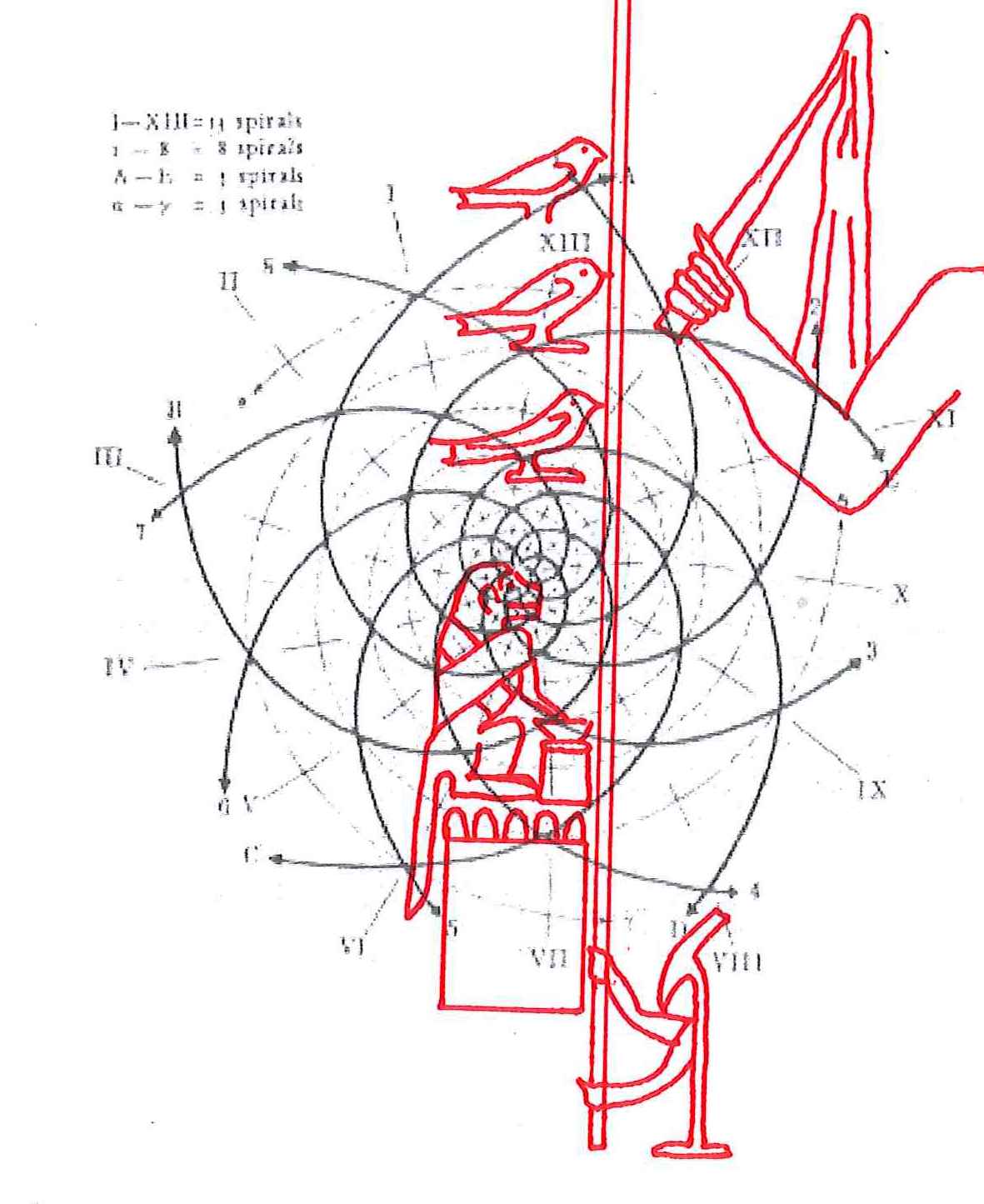
Maintenant, si nous essayons de projeter un schéma de ce genre sur l’image de la stèle que nous avons pris comme point de départ de notre analyse, « Djoser running », le résultat paraît pour le moins choquant, étant donné que l’espace intérieur de la stèle semble vraiment trouver un système de points caractéristiques exactement de la même manière que cela arrive dans le cas de l’inflorescence du tournesol. Nous avons choisi de partir de l’œil du Pharaon, en peu fondés sur des raisons historiques-symboliques (dans la culture de l’Ancienne Egypte l’œil humain est considéré un symbole divin), mais aussi parce-que, si nous procédons par tentatives et erreurs, ce point apparu tout d’abord même géométriquement plus significatifs que d’autres .
——————————
1 Voir en particulier la gallery, où les exemples de rapports entre les parties de cette stèle sont beaucoup plus nombreux de ceux que l’on voit dans le texte de l’article, et où on peut trouver de nombreux exemples de rapports d’or aussi dans les œuvres d’architecture et dans autres œuvres d’art de l’Ancienne Égypte – travaux appartenant à des périodes dynastiques et stylistiques même bien lointaines dans le temps.
2 Mais il a eu un cas – clairement le cas d’un très grand tournesol – où le rapport était 233/144.
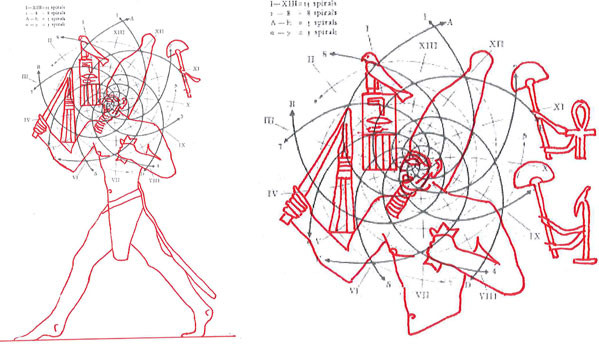
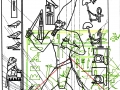
Déjà dans cet exemple nous voyons que le nombre de « intersections signifiantes » qu’il y a entre les spirales et le dessin de la stèle est assez remarquable, et que tous ces points ont comme caractéristique fondamentale celle de se trouver entre eux dans un rapport géométrique déterminé par le Nombre d’Or, même si d’une manière très compliquée (en pratique, on devrait obtenir la coordonnée de chaque point de cet étrange espace spiral à partir d’un système de logarithmes).
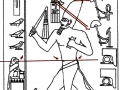
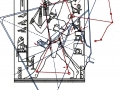
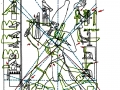
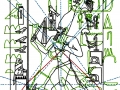
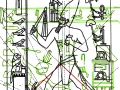
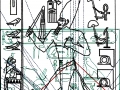
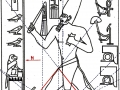
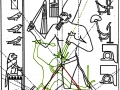
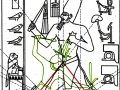
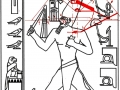
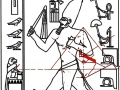
3. Il est tout à fait possible, et au moins intuitivement semble presque évident, que pour obtenir un espace où les points sont proches les uns des autres d’une manière suffisante pour obtenir des images figuratives et hiéroglyphiques complexes, il est nécessaire de supposer que cette subdivision en points de l’espace – qui de notre perspective paraît compliquée et assez difficile, pour ne pas dire bizarre ou même complètement absurde – part à son tour d’une multiplicité de pôles, même s’il n’est encore clair comment déterminer leur nombre exact. Par conséquent, il existe la possibilité que pour construire le dessin d’une stèle comme « Djoser running » ne suffit pas du tout, par exemple, partir d’un centre et passer d’un couple de nombres de Fibonacci contigus au couple suivant –comme on a vu qui se passe dans l’inflorescence de tournesols de grandes dimensions. Au contraire, il est possible que les pôles d’expansion de ces serrés tourbillons de spirales logarithmiques1 soient répartis de telle manière que dans tout l’espace de la stèle on puisse trouver, disons, un répartition équitable de points équitablement rapprochés – points dont les coordonnées résultent toujours et en tout cas par le croisement au moins de deux spirales (mais comme nous pouvons le voir à partir des images ci-dessus, certains points à ce moment sont déjà déterminés par le croisement de trois spirales : on peut imaginer que dans le progrès de la division et de la multiplication des pôles le nombre des spirales qui pour chaque point se superposent va augmenter de façon même vertigineuse et fait supposer que chaque point ne doive être enfin conçu que comme un pôle). Et, en effet, si nous déplaçons notre « tournesol » de l’œil du Pharaon dans autres points de la stèle choisi plus ou moins au hasard, voilà que nous constatons que le système des « intersections signifiantes » se recrée inexorablement
1C’est le nom de baptême “mathématique” de la spirale qui est peut-être la plus célèbre parmi les non-spécialistes avec le nom de « spirale de Fibonacci » (mais en réalité découverte par Jacques Bernouilli).
——————————
3 C’est le nom de baptême “mathématique” de la spirale qui est peut-être la plus célèbre parmi les non-spécialistes avec le nom de « spirale de Fibonacci » (mais en réalité découverte par Jacques Bernouilli).
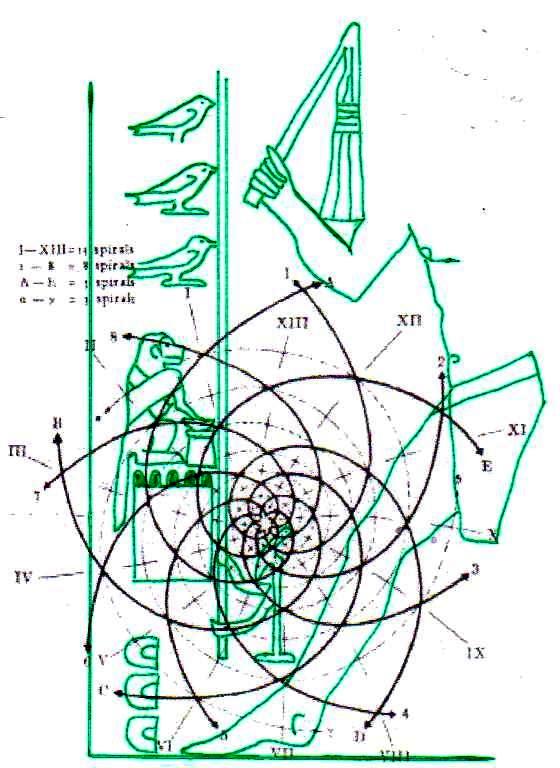
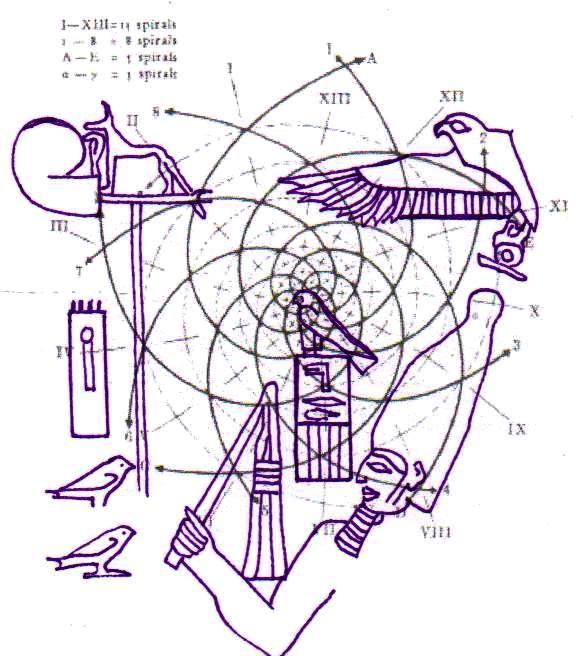
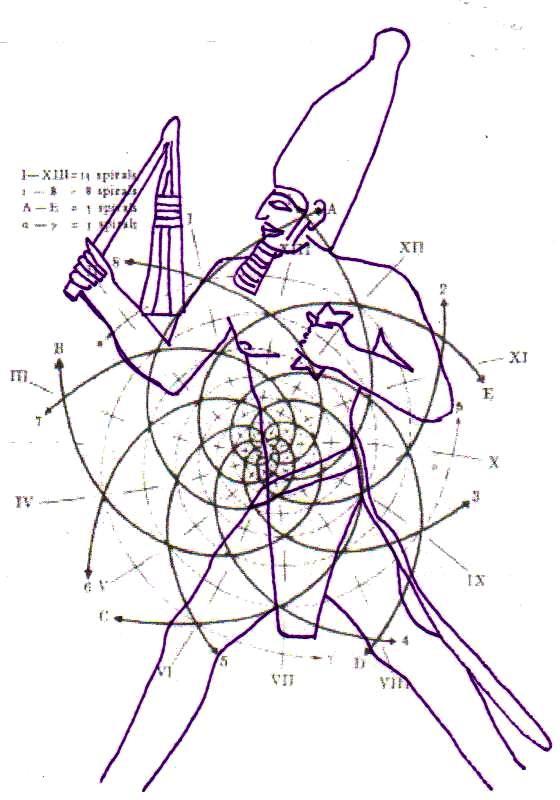
Maintenant, si on imagine d’avoir à disposition un espace divisé selon cette méthode, si on trace n’importe quel dessin et on relie les points déterminés par le croisement de deux ou plusieurs spirales, apparaît comme une conséquence logique et presque évidente le fait que entre ces points et les lignes qu’on a tracé au moyen de ces points existe une forme, même si complexe, de rapport d’or, exactement comme on la trouve à l’intérieur de l’inflorescence d’un tournesol.
4. Avec cette hypothèse il semble possible expliquer d’une façon relativement simple et satisfaisante tous ces phénomènes géométriques – à première vue plutôt incroyables – que nous avons vu dans les articles précédents et dont les exemples peuvent être trouvés abondamment dans les respectives gallery : les pyramides qui sont codifiées dans les stèles, les stèles où l’on recrée constamment le phénomène des « intersections signifiantes » même si la superposition se passe entre œuvres réalisées nombreux siècles plus tard (et donc par des artistes de différentes Dynasties) ou même dans le cas que l’on superpose le dessin d’une stèle sur lui-même. Et il est bon de rappeler que ces phénomènes géométriques – tout à fait surprenants et presque impensables dans des œuvres aussi anciennes – continuent à se produire, même dans le cas où on différencie le rapport entre les dimensions des images superposées.
Par exemple, nous avons déjà vu dans le premier article (Hypothèses de lecture de la stèle de Snéfrou) que la Pyramide Rouge reste toujours et de toute manière congruente avec parties et points géométriquement significatifs de la stèle, même dans le cas où on la projette à l’aide d’échelles plus petites ou plus grandes – et la même chose arrivait avec la Grande Pyramide, etc. Mais, si notre hypothèse est vraie, tous ces phénomènes géométriques trouveraient leur explication par une caractéristique fondamentale de la spirale logarithmique, qui est justement celle de maintenir de façon constante son module d’accroissement, de sorte que les proportions entre les spirales contiguës restent identiques soit si elles grandissent vers l’infiniment grand soit si elles diminuent vers l’infiniment petit. Donc, il est assez clair que toutes les figures construites sur la base de coordonnées du genre que nous avons vu ci-dessus restent toujours et de toute manière proportionnelles et congruentes entre elles d’une façon ou d’une autre (peut-être même d’une manière très compliquée), puisque les points de départ pour les tracer ont été identifiés et reliés par l’intermédiaire d’un système de spirales logarithmiques également congruentes.
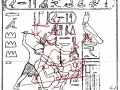
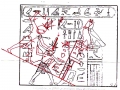
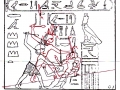
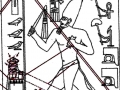
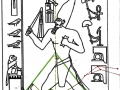
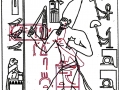
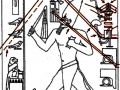
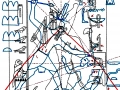
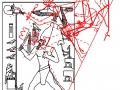
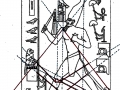
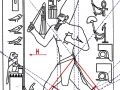
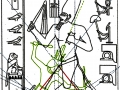
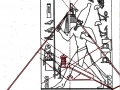
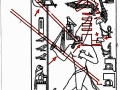
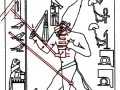
Mais il est essentiel à ce stade de rappeler que les phénomènes que nous avons analysés dans les deux articles précédents visaient aussi bien les Pyramides que les stèles, aussi bien les grands espaces architectoniques comme Gizeh et Dahshur que un cercle mégalithique « grossier » comme celui de Nabta Playa. Par conséquent on peut affirmer que pour toutes ces œuvres, quoique elles appartiennent à des époques et des styles différents et aient formes et fonctions très diverses, la méthode par laquelle les points de l’espace et l’espace lui-même étaient générés était la même, ou bien selon toute apparence assez semblable a ce que nous trouvons dans la nature dans l’inflorescence du tournesol. Et tout de suite nous pouvons fonder cette affirmation – qui à première vue peut paraître audacieuse – à travers les images qui suivent, où l’on peut voir que on retrouve cette façon vraiment très particulière de déterminer les coordonnées des points dans des stèles d’une époque très différente de celle où a été sculpté « Djoser running » (probablement 2700-2800 a.C.). Il s’agit de la stèle de Snéfrou du Sinaï, de celle de Ramsès II et de celle de Sétis I
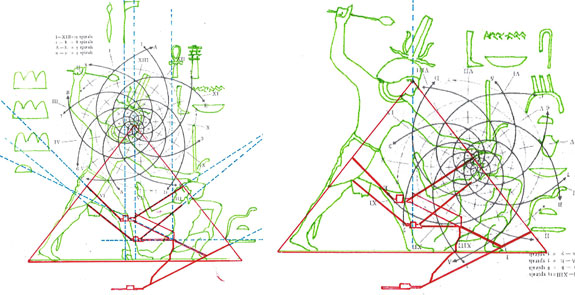
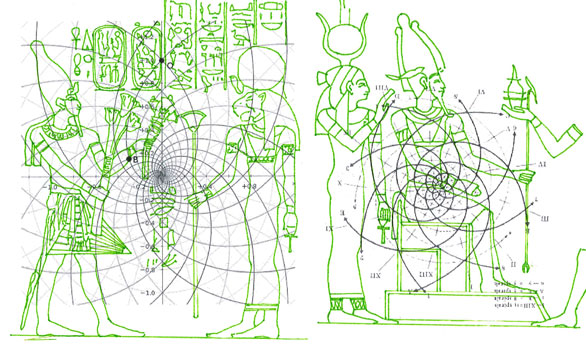
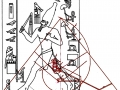
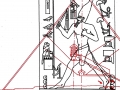
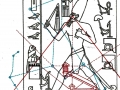
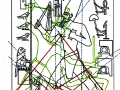
De ce que nous pouvons voir à travers ces images – bien que pas encore en possession d’une formule dérivée – par l’évidence visuel-géométrique nous sommes motivés à formuler l’hypothèse que dans la culture égyptienne de l’antiquité à la base de tout l’art figuratif – et bien sûr de l’ensemble de l’architecture, à commencer par les pyramides de la IV Dynastie, qui en fait semblent énormément plus anciennes que les autres – il n’y a aucune intuition esthétique dans le sens où nous sommes amenés à comprendre ces mots dans la modernité, mais plutôt une intuition géométrique-mathématique, dont les origines sont probablement astronomiques. En fait, avec toute évidence, les figures ci-dessus ne peuvent être obtenues à partir d’un exemplaire de la réalité fait – pourrait-on dire – d’une manière approximative sur une feuille blanche ; au contraire, il semble qu’elles furent obtenues par moyen de l’union des points identifiés grâce – pour ainsi dire – à un système de « tourbillons » de spirales logarithmiques, de sorte que ce qui est décisif pour la détermination de leurs contours et de leurs proportions n’est pas l’ « œil » de l’artiste, mais la fonction mathématique par laquelle elles sont générées. Et cette affirmation nous résulte plus croyable et au même temps plus incroyable quand on se rend compte que le diagramme projeté sur la stèle de Ramsès n’est pas celui de l’inflorescence du tournesol, mais plutôt un diagramme bidimensionnel de l’espace-temps réalisé par Vincenzo Fappalà et publié sur ASTRONOMIA.com (Deux autres découvertes feront l’objet d’un travail que nous allons développer prochainement. Il s’agit de découvertes que on peut définir tant archéoastronomiques que astronomiques en sens absolu – elles aussi sont également impressionnantes, mais en un certain sens moins inattendues – et sont à la base de cette hypothèse) que nous pouvons voir dans l’image ci-dessous.
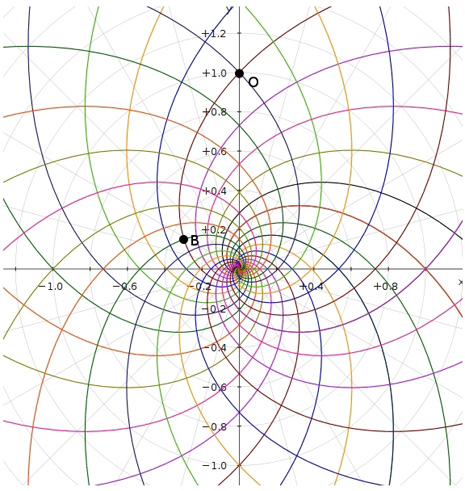
On peut noter comme ce diagramme semble déjà à première vue mieux décrire le système géométrique d’où découlent les stèles de l’Ancienne Égypte et, en fait, si nous l’ « appuyons » sur la stèle de Snéfrou (image ci-dessous), ce diagramme semble « jouer » de façon plus efficace ; ni après ce que nous avons vu dans les articles précédents nous sommes surpris de découvrir que cela s’applique aussi à la Grande Pyramide et d’autres reliefs de l’Ancienne Égypte, Djoser Running y compris
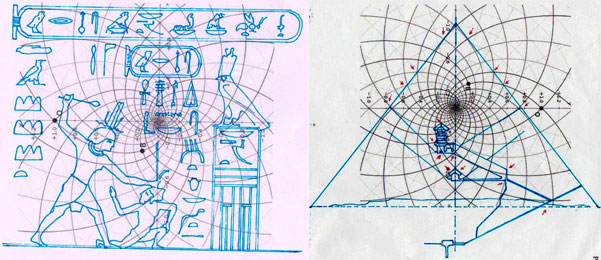
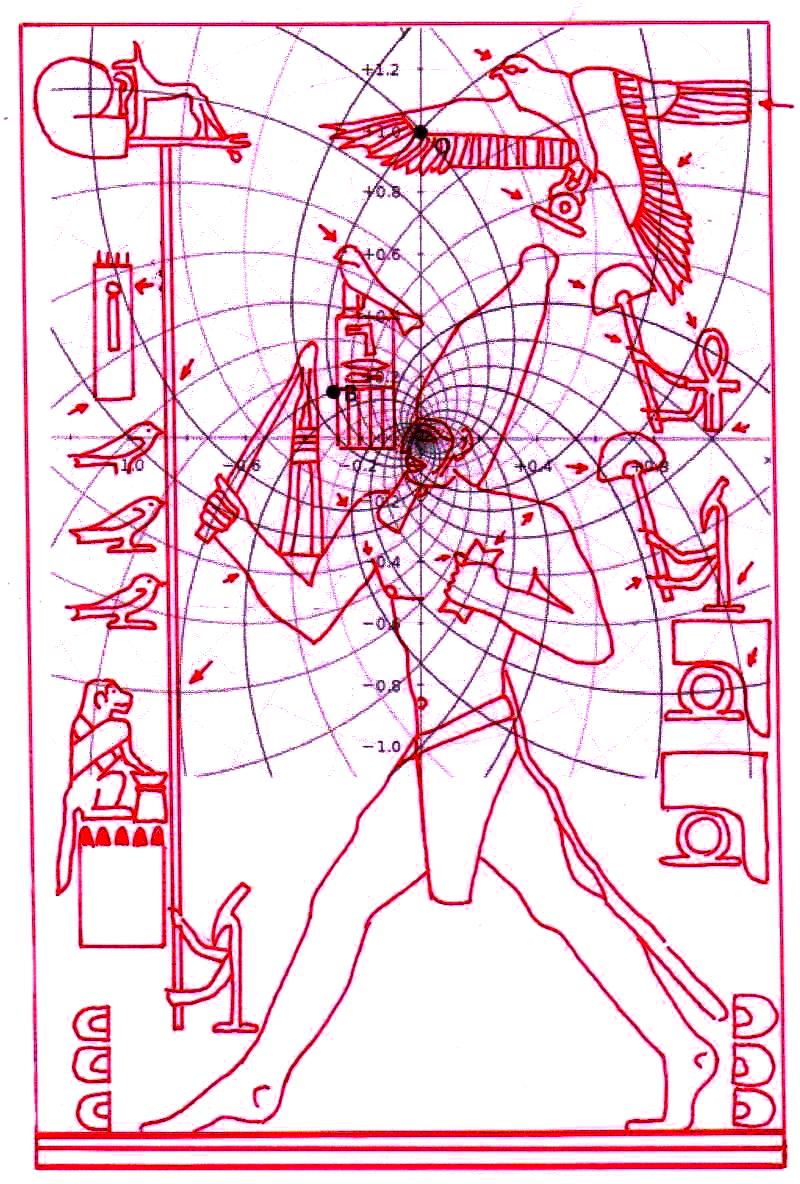
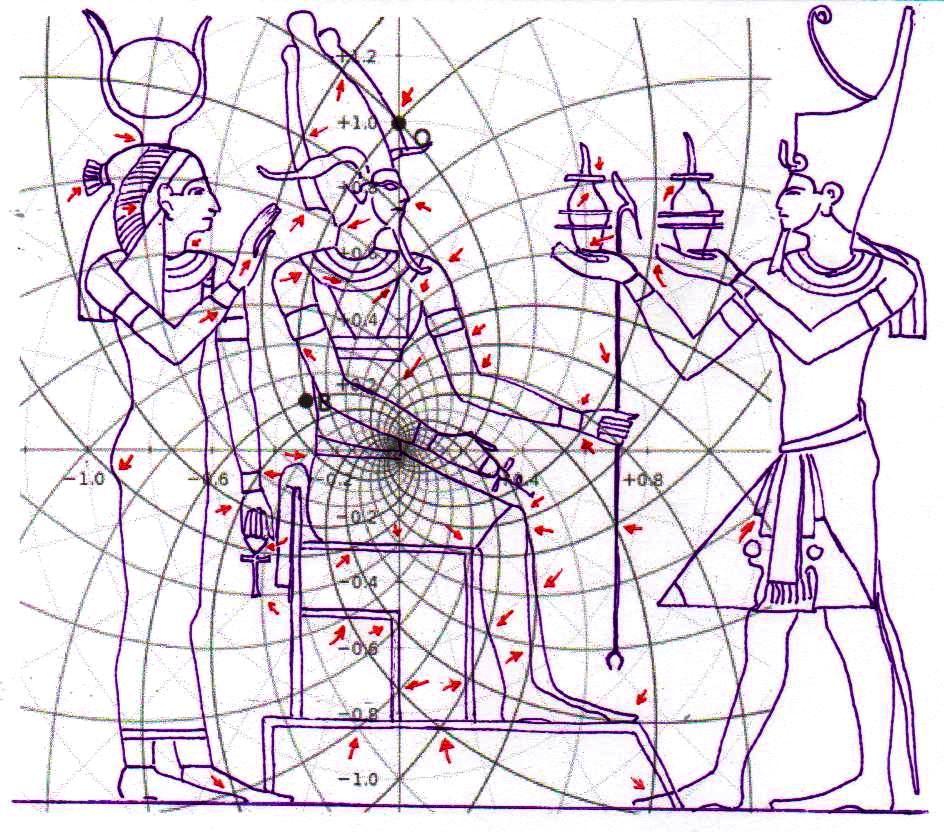
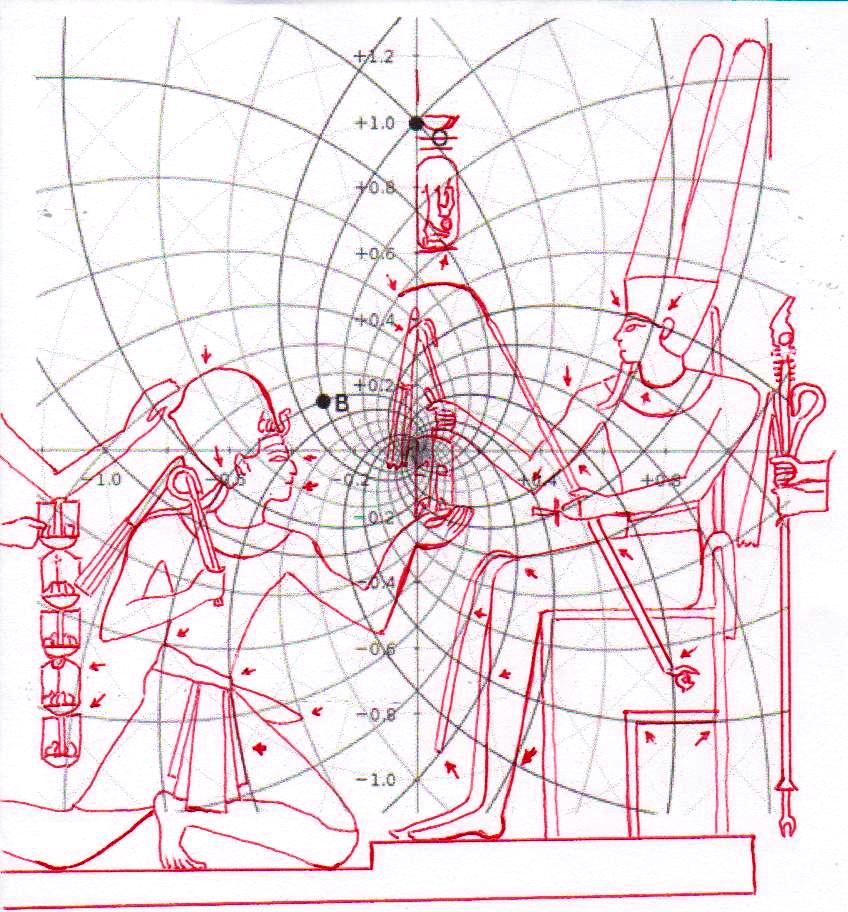
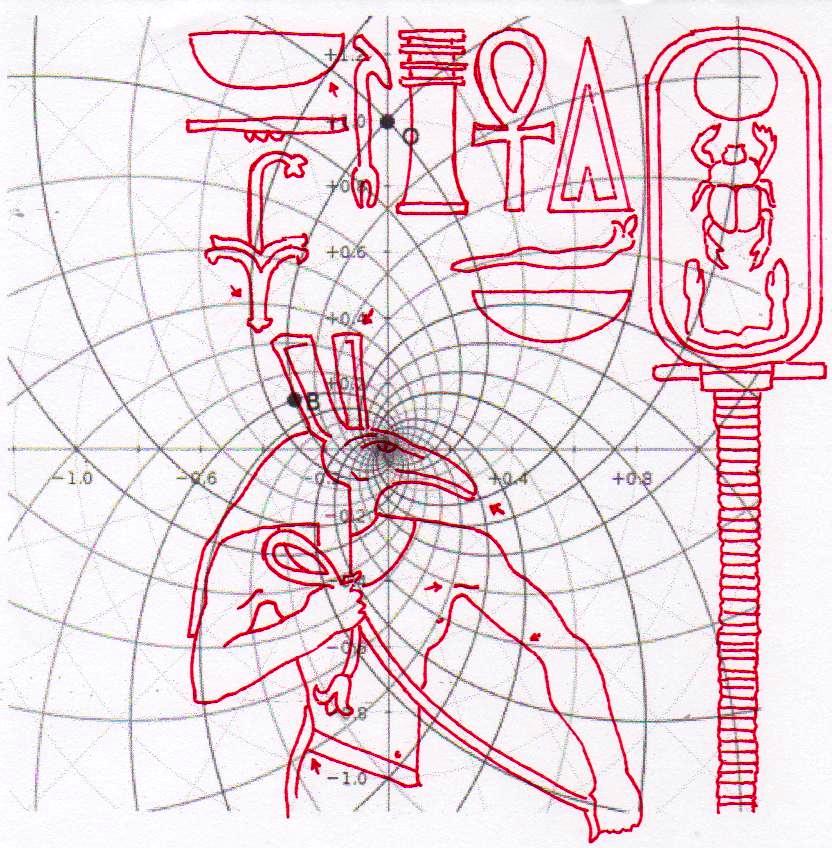
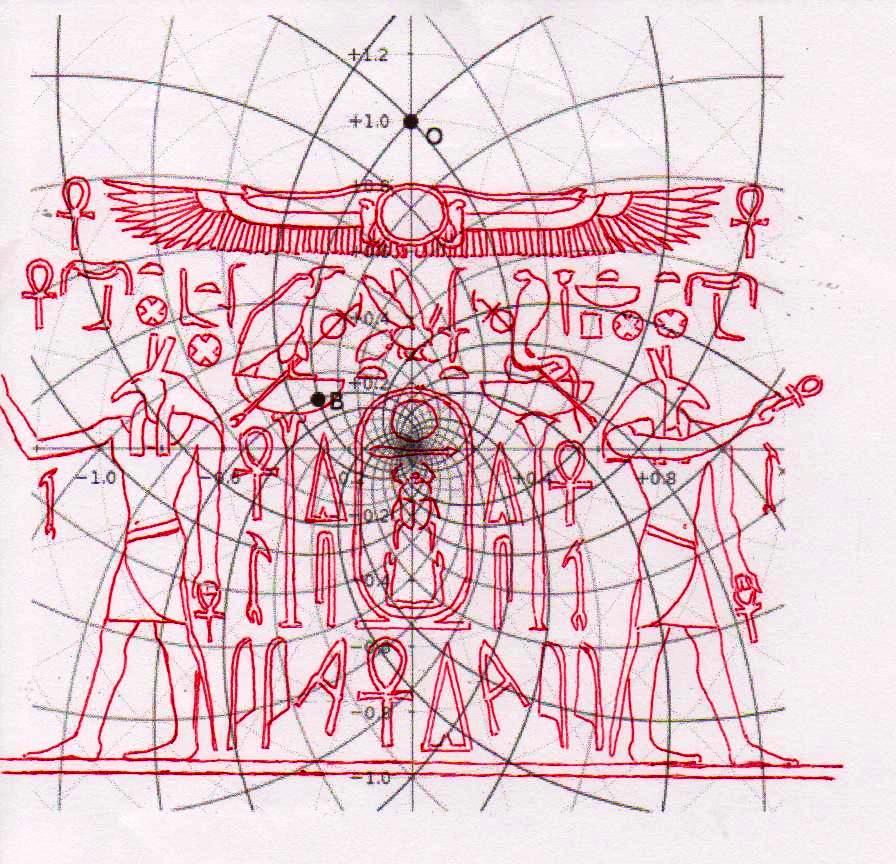
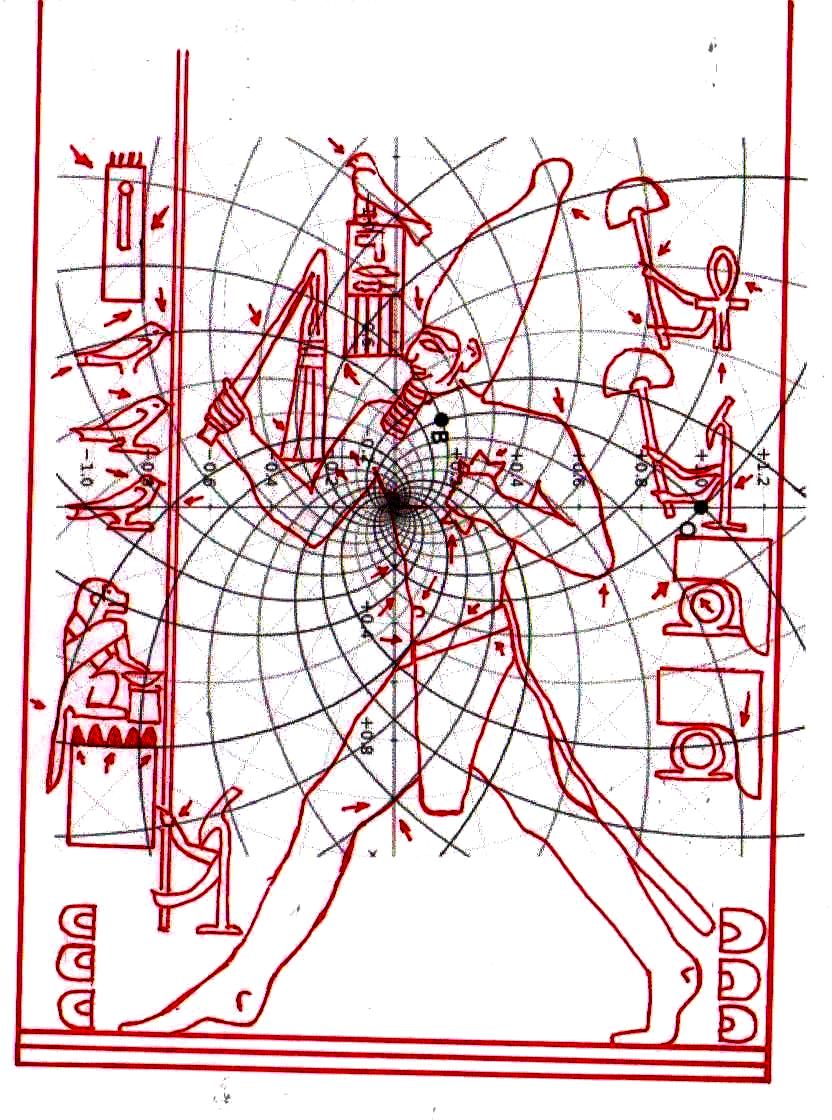
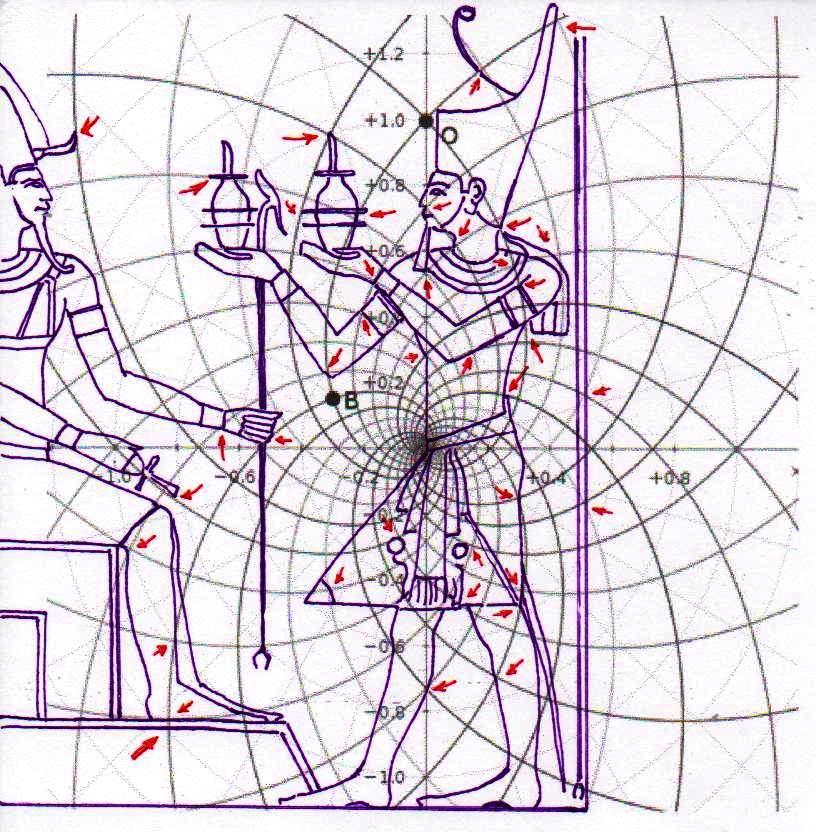
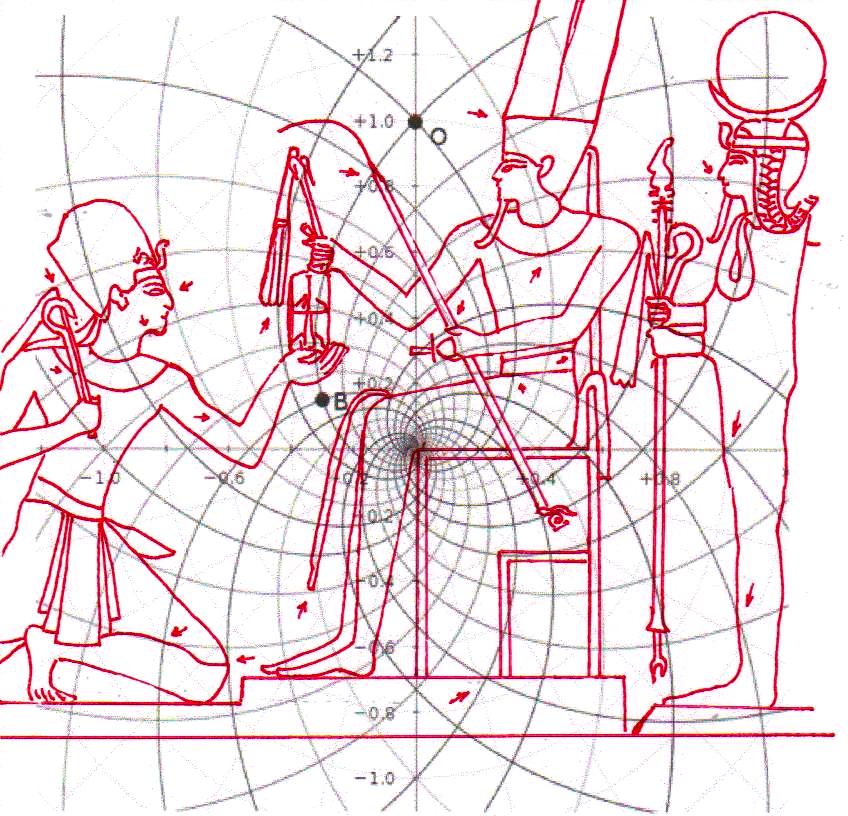
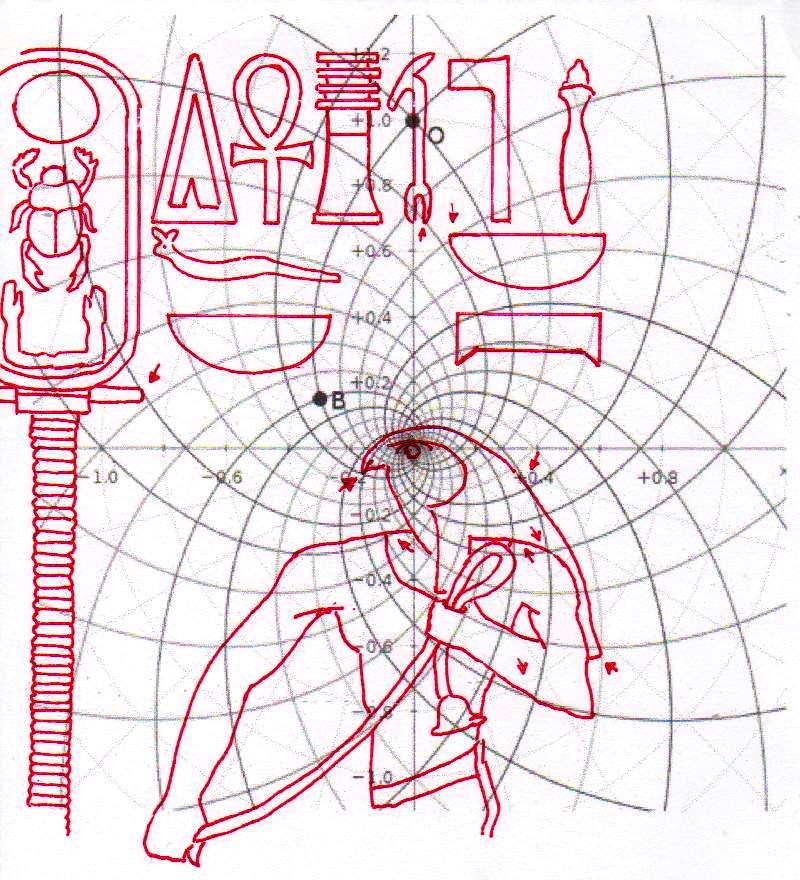
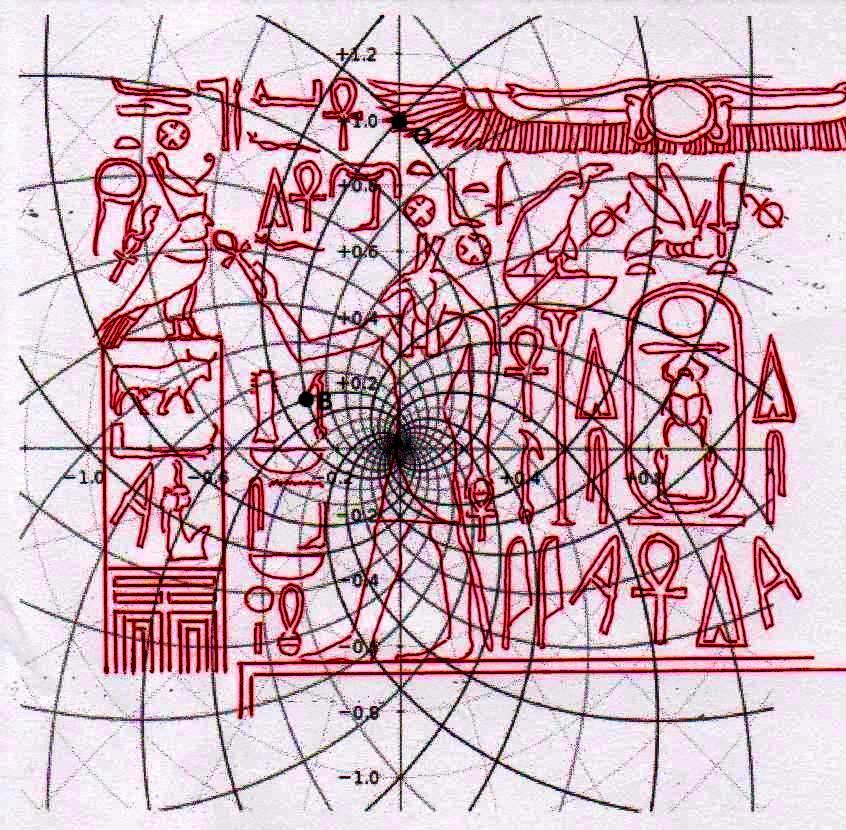
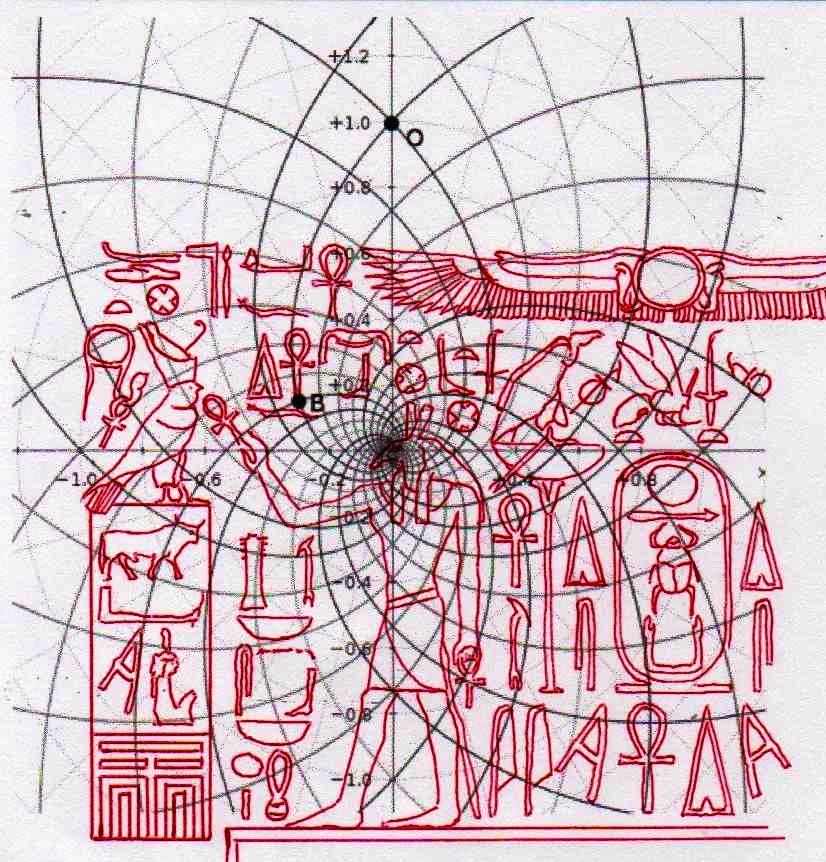
Le choc qui peut être la conséquence de l’analyse attentive de ces images – comme il arrive chaque fois que l’on constate que en temps proches du Néolithique on avait à disposition des instruments techniques et donc intellectuels égaux ou même supérieurs à ces de la modernité – peut pousser à tourner sa tête ailleurs et faire semblant de rien. Nous avons été formés dans une conception dogmatiquement évolutionniste ; alors, quand nous découvrons des traits d’extraordinaire dans les mathématiques ou dans l’astronomie de peuples très anciens, nous inclinons à tout expliquer à travers le cas et à aller de l’avant avec nos confortables dogmes historiographiques. Mais soumettons une fois encore à notre attention l’image de la Grande Pyramide et examinons les points caractéristiques déterminé par le diagramme de Fappalà : de cette manière nous pourrons nous rendre compte jusqu’au fond combien ces deux figures sont presque logiquement liées .
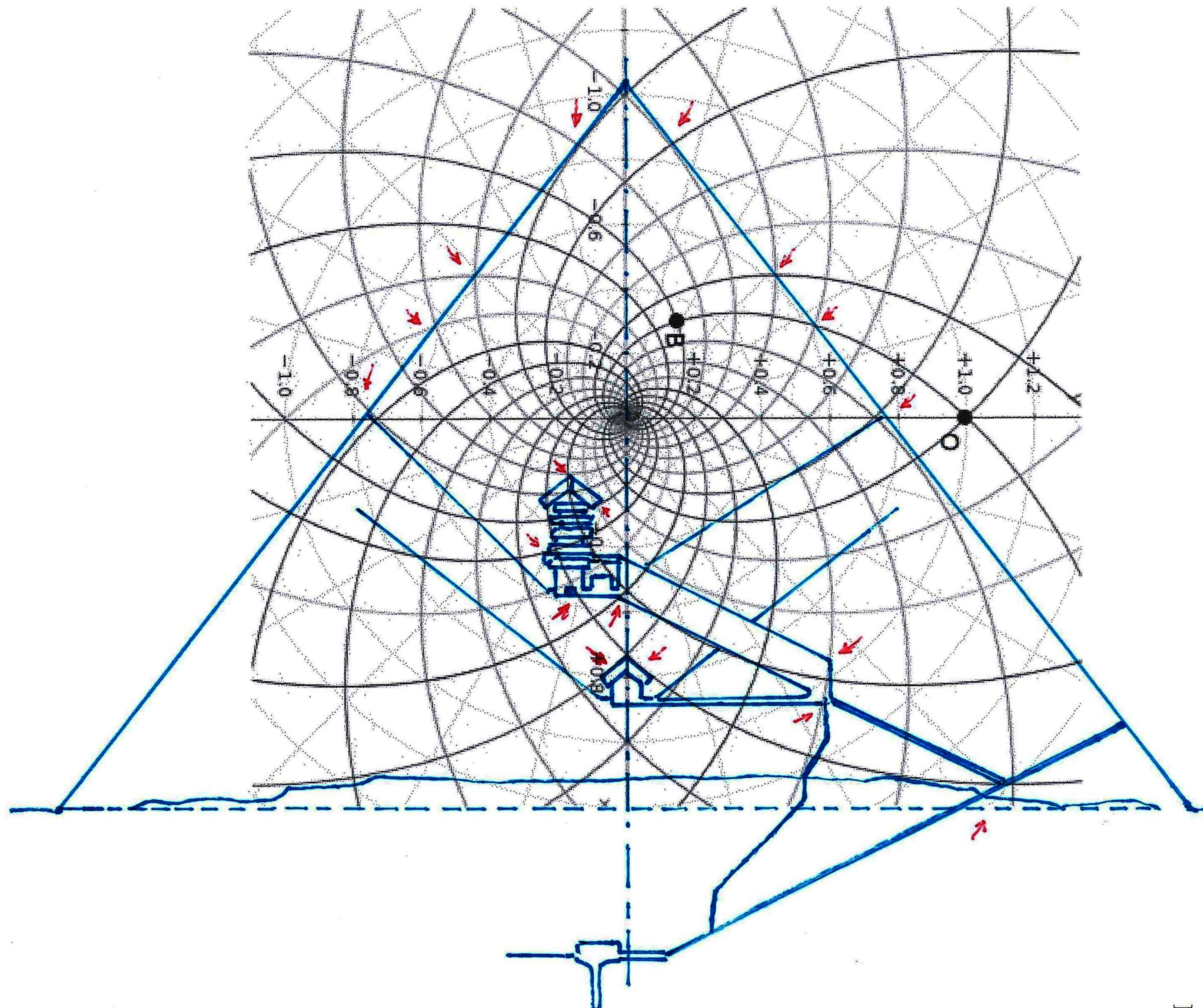
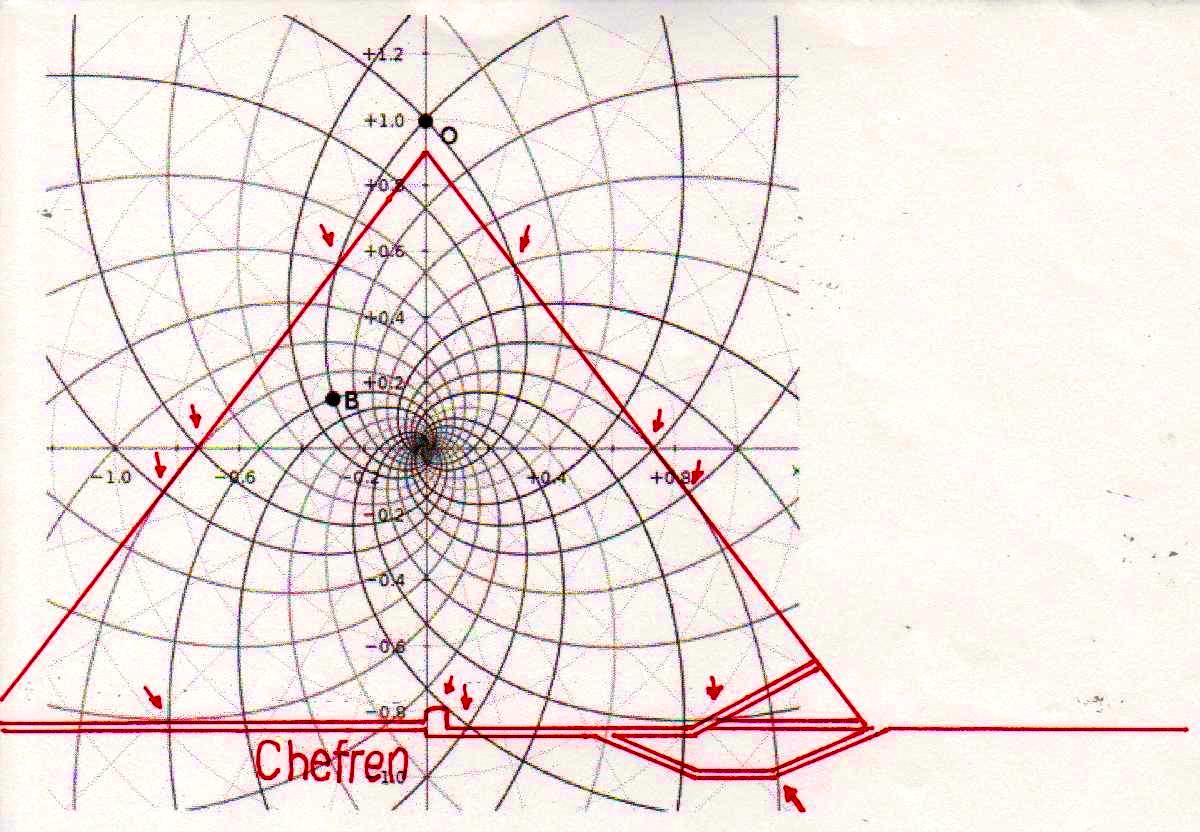
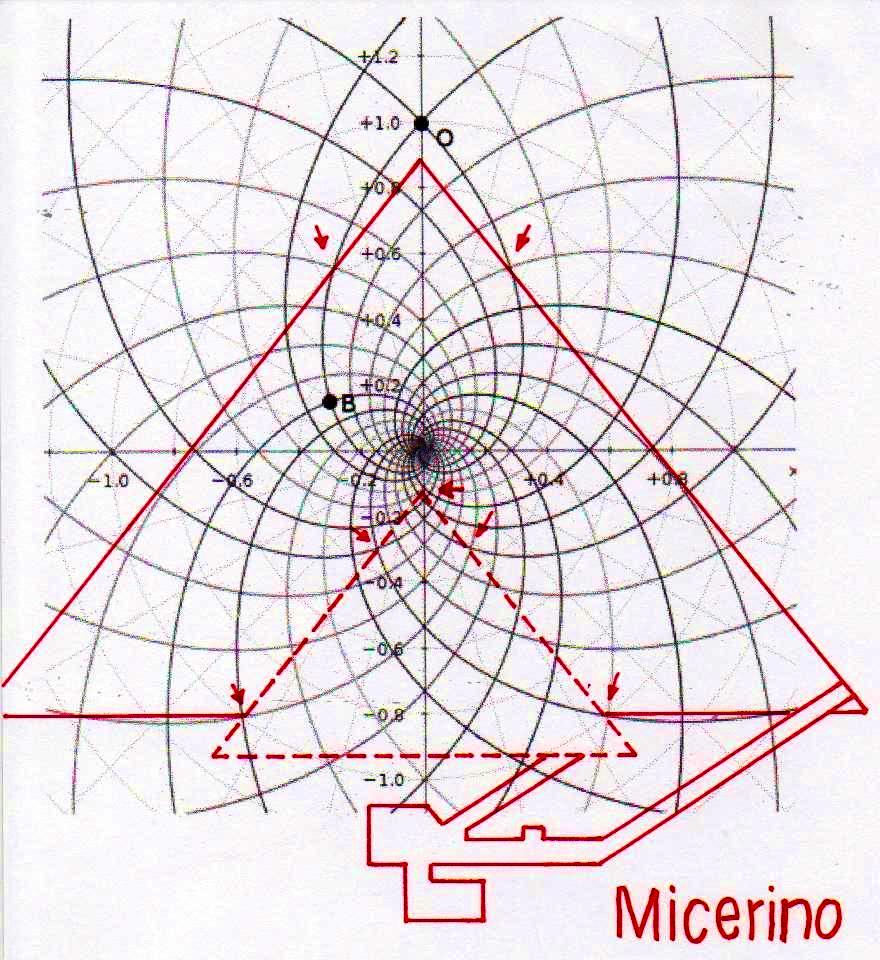
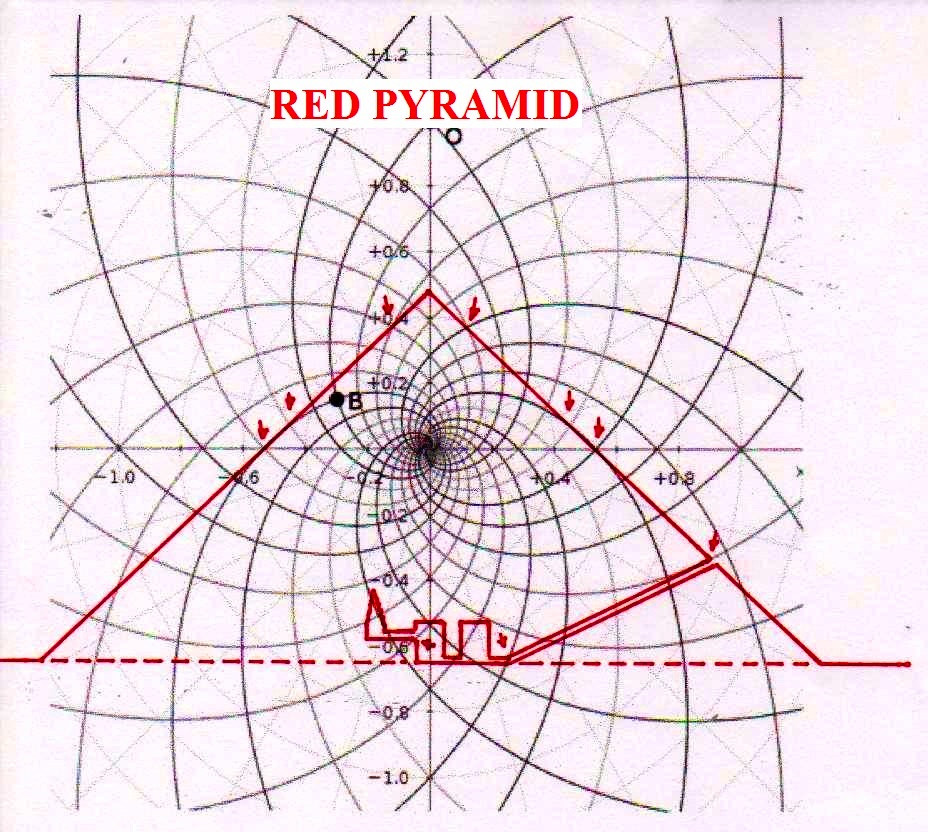
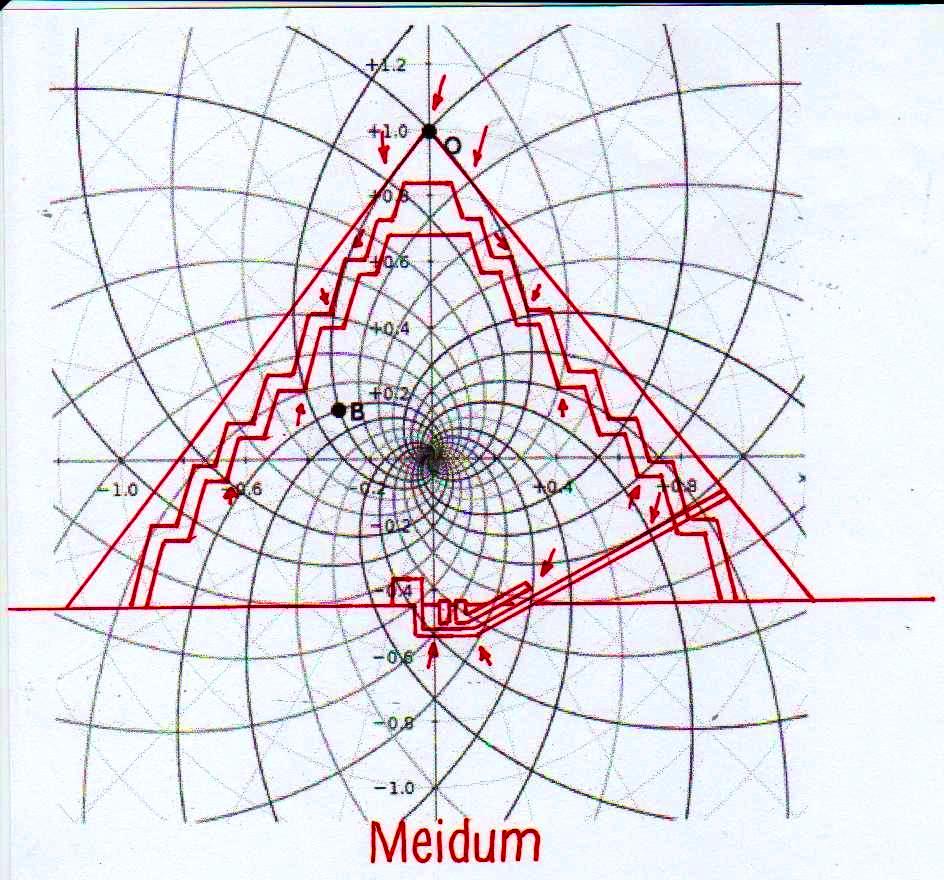
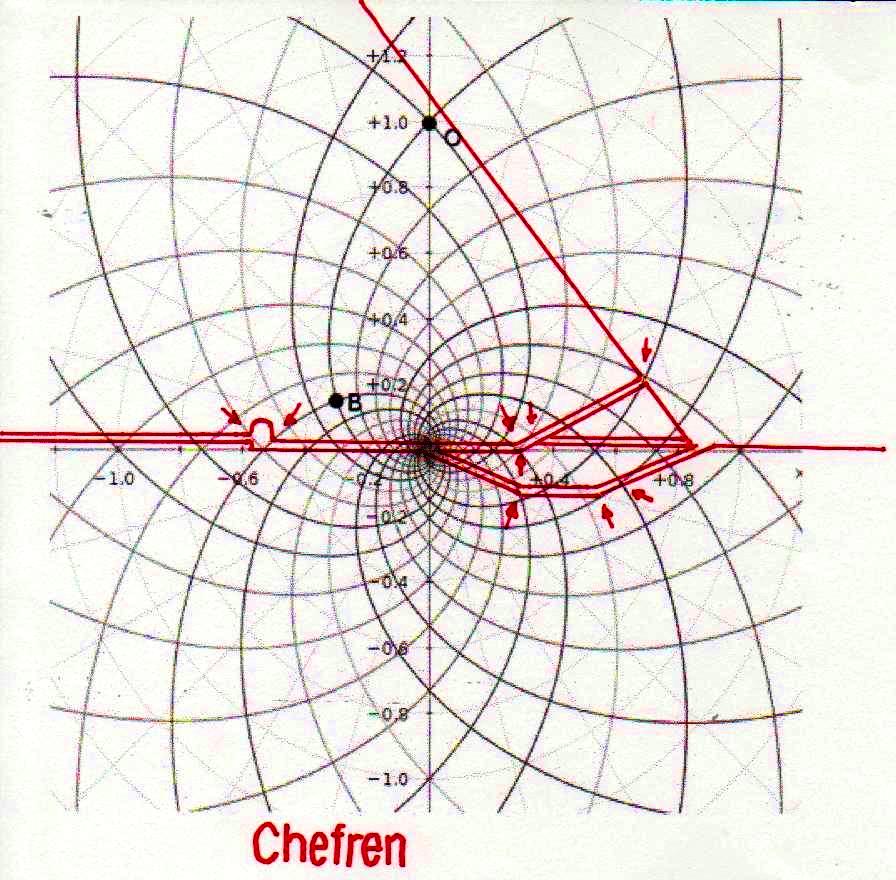
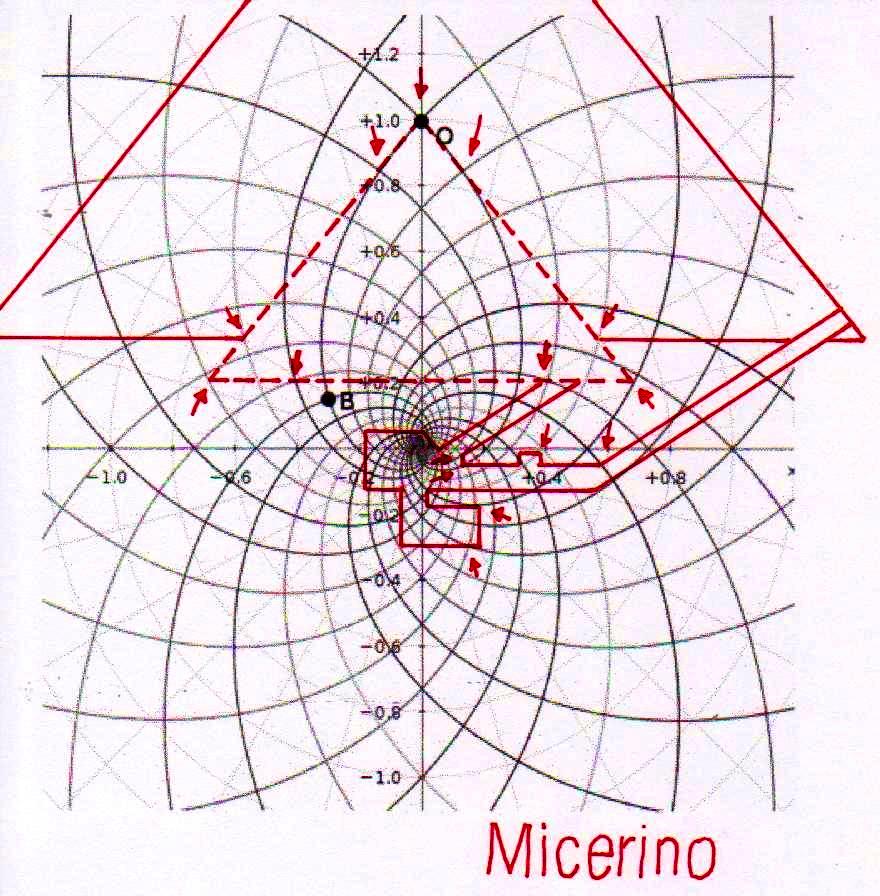
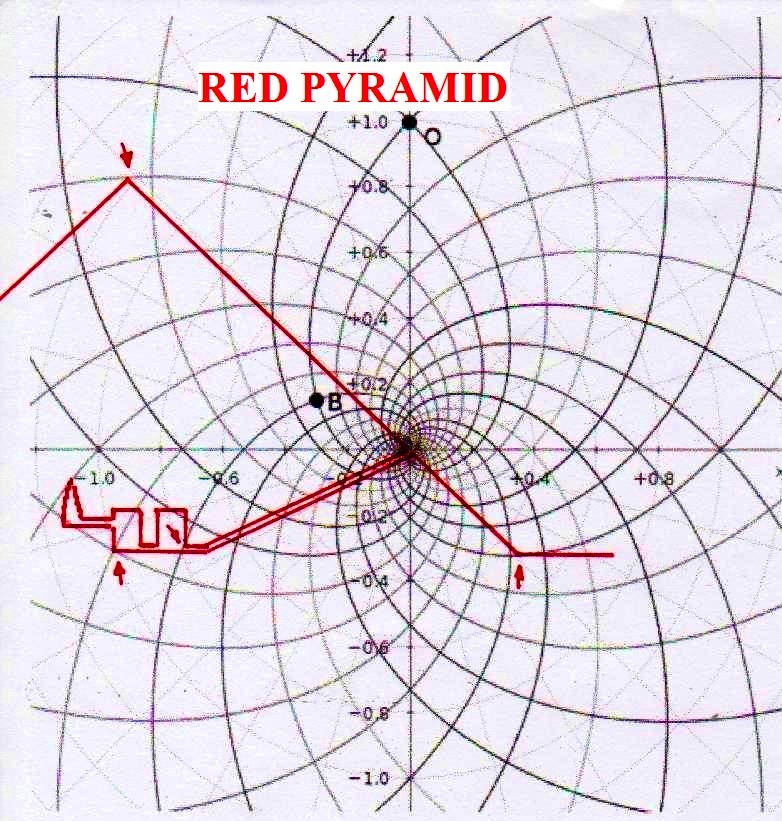
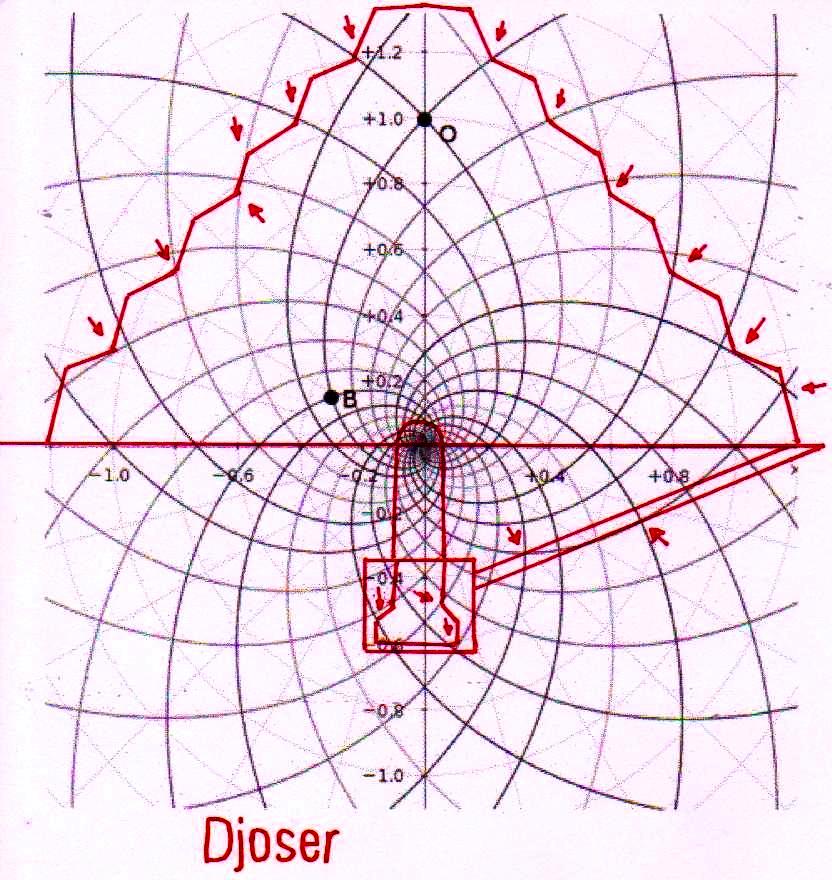
C’est pourtant bien difficile de penser que cette façon de coder des notions mathématico-scientifiques avait le but de les garder ou même de les communiquer à la postérité, parce que – seulement pour faire an exemple – des hommes qui ignorent la Théorie de la Relativité et des ses possibles représentations géométriques ne pourraient en aucune manière comprendre que cette théorie est contenue dans ses proportions. Dans la tradition copte il y a des récits, où l’on dit que dans en temps très éloigné un roi fit construire la Grande Pyramide pour inscrire en elle tout le savoir que l’on avait de son temps : mais cette même tradition – au moins dans la forme qui nous est arrivée, ne semble en aucune manière consciente des contenus effectifs de ce savoir, même si la suggestion qu’elle contient semble confirmée par la découverte de ce qui apparaît come l’essence profonde de la géométrie du monument.
partie seconde : LA THÉORIE DE LA RELATIVITÉ DANS LE TIMÉE DE PLATON
1. De temps en temps il peut arriver de lire des choses qui étonnent, dans le sens que nous ne pensons pas possible de les lire là, où, en fait, nous les lisons. Leur signification semble évidente, mais c’est comme si nous ne pouvions pas les comprendre, parce que nous avons été formés à penser que leur signification doit être différente de ce que nous voyons. Pour expliquer ce concept, peut-être il n’y a pas de meilleur exemple de ces mots que l’on retrouve dans le Timée (62 C – 63 A).
« Pour le lourd et le léger, c’est en les considérant en même temps que la nature de ce qu’on appelle le haut et le bas qu’on les expliquera le plus clairement. Qu’il y ait naturellement deux régions opposées qui partagent l’univers en deux, l’une étant le bas, vers lequel tombe tout ce qui a une certaine masse corporelle, et l’autre le haut, où rien ne s’élève que par force, c’est une erreur complète de le croire. En effet l’univers, étant complètement sphérique, tous les points qui, étant à égale distance du centre, sont ses extrémités sont tous pareils en tant qu’extrémités, et le centre, distant dans la même mesure de tous les points extrêmes, doit être conçu comme opposé à eux tous.
Ce passage, tel qu’il est, semble très obscur. Mais un point de clarté est représenté par la déclaration que « tous les points qui, étant à égale distance du centre, sont ses extrémités sont tous pareils en tant qu’extrémités ». Cette déclaration semble en contenir une autre qui, au moins pour le fait que nous l’avons entendu répéter plusieurs fois, nous paraît plus familière. En fait, au moins en ce qui concerne le monde tel que nous le voyons tous les jours, nous sommes obligés de penser que si toutes les choses sont par nature à l’extrémité de la même manière, par conséquent, toutes les choses doivent se trouver dans le centre – ou que toutes peuvent être considérées le centre de la même manière (nous verrons bientôt pourquoi nous sommes arrivés à cette conclusion que le lecteur expert de physique et de logique aura tiré spontanément tout seul).
Donc, il semble que, d’une manière un peu hermétique, Platon, en parlant du monde comme d’une sphère, se rapporte à une conception que l’histoire attribue à Hermès Trismégiste (l’équivalent grecque classique de l’ancien dieu égyptien de la sagesse, le dieu Toth) , et non pas à celle du sens commun. C’est quelque chose que l’on peut déduire également à partir de la description qu’il donne de la production du monde (Timée 33 B , 34 B )
« Pour la forme, il lui a donné celle qui lui convenait et avait de l’affinité avec lui. Or la forme qui convenait à l’animal qui devait contenir en lui tous les animaux, c’était celle qui renferme en elle toutes les autres formes. C’est pourquoi le dieu a tourné le monde en forme de sphère, dont les extrémités sont partout à égale distance du centre, cette forme circulaire étant la plus parfaite de toutes et la plus semblable à elle-même, car il pensait que le semblable est infiniment plus beau que le dissemblable. En outre, il arrondit et polit toute sa surface extérieure pour plusieurs raisons.
(…)
C’est par toutes ces raisons que le dieu qui est toujours, songeant au dieu qui devait être un jour, en fit un corps poli, partout homogène, équidistant de son centre, complet, parfait, composé de corps parfaits. »
Or, il est évident que le monde tel qu’il s’offre à l’observation immédiate n’est pas du tout de cette façon. De plus, il semble particulièrement absurde l’idée d’une sphère en trois dimensions sans un dehors, ou immergée dans un espace qui est comme un rêve ou un cauchemar, comme il est dit dans le Timée, 52, B.
« Enfin il y a toujours une troisième espèce, celle du lieu, qui n’admet pas de destruction et qui fournit une place à tous les objets qui naissent. Elle n’est elle-même perceptible que par un raisonnement bâtard où n’entre pas la sensation ; c’est à peine si l’on y peut croire. Nous l’entrevoyons comme dans un songe, en nous disant qu’il faut nécessairement que tout ce qui est soit quelque part dans un lieu déterminé, occupe une certaine place, et que ce qui n’est ni sur la terre ni en quelque lieu sous le ciel n’est rien. A cause de cet état de rêve, nous sommes incapables à l’état de veille de faire toutes ces distinctions et d’autres du même genre, même à l’égard de la nature éveillée et vraiment existante, et ainsi d’exprimer ce qui est vrai »
Par conséquent, nous devons essayer de comprendre quel est le sens que peut avoir cette étrange description de Platon.
2. En effet, si l’on considère le niveau du sens commun, l’affirmation selon laquelle toutes les parties de l’univers se trouvent à égale distance du centre comme les points de la superficie d’une sphère n’est qu’un non sequitur. En effet, on suppose que le centre de l’univers évoqué par Platon correspond réellement au centre de la Terre, comme des nombreux commentateurs ont proposé sur la base de l’affirmation qui se trouve dans le Timée 40 :
« Pour la terre, notre nourrice, enroulée autour de l’axe qui traverse tout l’univers, Dieu la disposa pour être la gardienne et l’ouvrière de la nuit et du jour, la première et la plus ancienne des divinités qui sont nées à l’intérieur du ciel. »
Comme on peut bien voir, dans le Timée la Terre, comme d’ailleurs toutes les autres entités célestes, est conçue de la même manière dont nous la concevons, c’est-à-dire comme une sphère qui tourne sur elle-même : un fait de quoi, d’ailleurs, on était bien conscient dans presque toutes les conceptions antiques et soi-disant « primitives ». En effet, l’idée que dans l’antiquité généralement on croyait que la Terre était plate, c’est n’est rien qu’une superstition moderne, causée par le fait que l’on n’a pas réalisé que dans les cosmologies antiques avec le mot “terre” généralement on n’entendait o pas la planète Terre, mais plutôt le plan de l’écliptique (qui, par exemple, dans l’Apocalypse est appelé la « Jérusalem céleste », avec les douze portes qui ne sont rien de plus que les douze « maisons » du zodiaque ; dans la légende du roi Arthur il y avait la table ronde avec les Douze Chevaliers ; le fils de Parzival, Lohengrin, voyageait sur un bateau tiré par un cygne, une claire allusion à la constellation du Cygne ; dans la version de Wolfram von Eschenbach le temple du Saint-Graal est « lisse et arrondi comme par le travail d’un tour », tout comme l’univers décrit dans le Timée, etc.).
Mais si Platon était conscient de notions astronomiques si raffinées, il devient difficile de comprendre comment il aurait pu venir à croire que l’univers est une sphère absolument uniforme, car toutes les observations ordinaires démentent immédiatement cette hypothèse. La pointe des montagnes n’est pas, évidemment, à la même distance du centre de la Terre que le fond de la mer. À leur tour, les nuages sont plus loin du centre de la Terre que la pointe des montagnes, et la lune plus que les nuages, etc. Même les enfants le savent. Donc, comment est-il possible que Platon ne le savait pas, vu qu’il possédait des connaissances beaucoup plus profondes?
3. Cependant, en dépit de toute évidence sensible, Platon insiste longuement sur le concept de l’uniformité absolue de l’univers, et semble vouloir à tout prix dissuader ses lecteurs de l’idée que dans l’univers pourrait exister un endroit qui peut être appelé haut ou bas, même dans un sens relatif
« Le monde étant ainsi disposé, quel est celui des points en question qu’on peut mettre en haut ou en bas, sans être justement blâmé de lui imposer un nom tout à fait impropre ? S’agit-il du lieu qui est au milieu du monde, il n’est pas juste de dire qu’il est naturellement bas ou haut, il en est simplement le centre. Quant au lieu qui l’entoure, il n’est pas le centre et ne contient aucune partie qui soit différente d’une autre et plus près du centre que l’une quelconque des parties à l’opposite. Or comment peut-on appliquer des noms contraires à ce qui est exactement de même nature, et comment croire qu’alors on parle juste ? »
Mais ici il faut noter une fois de plus que l’affirmation selon laquelle l’univers est une entité « uniforme dans toutes ses parties » ne peut absolument pas se référer à l’univers de la perception sensorielle. C’est parce que, comme il est clair pour tous, si nous choisissons dans l’univers physique un point quelconque comme son centre, immédiatement nous remarquons qu’il y a des endroits qui sont plus proches ou plus lointains de ce point. Mais Platon insiste à nouveau dans son idée
« Supposons, en effet, qu’il y ait un corps solide en équilibre au centre de l’univers : il ne se porterait jamais à aucune des extrémités à cause de leur parfaite similitude. Supposons encore que quelqu’un fasse le tour de ce corps il se trouverait souvent antipode de lui-même et il appellerait bas et haut le même point de ce corps. Puisque, comme nous venons de le dire, le tout est sphérique, il n’y a pas de raison d’appeler tel endroit bas, tel autre haut. D’où viennent donc ces dénominations et à quoi s’appliquent-elles dans la réalité pour que nous en ayons pris l’habitude de diviser ainsi tout le ciel lui-même et d’en parler en ces termes ? »
4. Cette position de Platon, prise superficiellement, semble être une ergoterie sur des idées abstraites, pas une description du cosmos. Supposons que la Terre est vraiment le centre de l’Univers. Si nous prenons les points qui sont à la même distance de son centre, nous constatons que si nous nous plaçons maintenant dans une place, maintenant dans l’autre, nous sommes tentés de définir le même point maintenant comme bas maintenant comme élevé, et donc nous tomberont dans la contradiction. Mais le fait demeure que l’univers n’est pas une sphère uniforme, et, par conséquent, il n’est pas vrai que toutes les entités qui le composent sont situées à la même distance de son centre. Même si nous mettons en œuvre la révolution copernicienne et prenons le soleil comme centre de l’univers, on remarque tout de suite qu’il existe des planètes qui sont plus près de lui et d’autres plus éloignées. Si nous prenons une étoile quelconque, la conclusion à laquelle nous arrivons ne peut être que la même. En outre, dans le Timée, il y a des preuves concluantes que Platon, loin d’être un naïf, était bien au courant de ces choses, car il parle de sphères plus proches ou plus éloignées de l’axe de la Terre. Alors pourquoi insiste-il sur l’idée que l’univers est absolument uniforme?
Afin de donner un sens à cette partie du Timée nous devons nous éloigner du sens commun, et de la normale sphère euclidienne, et penser, pour ainsi dire, à la « sphère absolue » dont parle Hermès Trismégiste quand il dit que « l’univers est une sphère dont le centre est partout et dont la surface est nulle part ». C’est seulement à partir d’un concept de ce genre que nous pouvons raisonnablement dire que toutes les entités qui composent l’univers sont à la même distance exacte du centre. Elles sont toutes situées à la même distance du centre, parce que chaque point de l’espace est conçu comme un centre possible. Mais comme nous entrons dans un tel espace, nous ne pouvons jamais atteindre un point de vue que l’on puisse définir un « centre unique et absolu ». Au contraire, dans le domaine de cette sphère chacun de ses centres infinis est un centre absolu, car cette sphère est constituée exclusivement de points-centre.
5. Aucun commentateur moderne postérieur à l’invention de la théorie de la relativité a remarqué ou osé remarquer, que la sphère mentionnée par Hermès Trismégiste (et par conséquent aussi par Platon) est une métaphore parfaite de l’espace relativiste. Ce n’a pas été remarqué non plus par les lecteurs avec une profonde connaissance scientifique, ni par les scientifiques eux-mêmes. Pourtant, selon la théorie d’Einstein, tout comme dans la sphère d’Hermès Trismégiste (et donc aussi de Platon), chaque point de l’espace qui nous entoure a la même dignité par rapport à l’ensemble. Par conséquent , chacun des points de l’univers est un point de vue tout aussi valable qu’un autre pour obtenir une description vraie de l’univers. Traduit en termes modernes, nous disons que chaque point de l’espace est un des infinis centres absolus de l’univers relativiste.
Cette affirmation prend une plus grande consistance quand on se souvient que Platon était l’héritier, grâce à Socrate, de la pensée de Pythagore, qui en grande partie dérivait du contact avec la culture hermétique égyptienne. L’indice le plus évident est la manière dont Platon décrit le phénomène de la vision dans le Timée 45 , B , C.
« Les premiers organes qu’ils fabriquèrent furent les yeux porteurs de lumière ; ils les fixèrent sur le visage dans le but que je vais dire. De cette sorte de feu qui a la propriété de ne pas brûler et de fournir une lumière douce, ils imaginèrent de faire le propre corps de chaque jour, et le feu pur qui est en nous, frère de celui-là, ils le firent couler par les yeux en un courant de parties lisses et pressées, et ils comprimèrent l’œil tout entier, mais surtout le centre, de manière qu’il retînt tout autre feu plus épais et ne laissât filtrer que cette espèce de feu pur. Lors donc que la lumière du jour entoure le courant de la vision, le semblable rencontrant son semblable, se fond avec lui, pour former dans la direction des yeux un seul corps, partout où le rayon sorti du dedans frappe un objet qu’il rencontre à l’extérieur.
Ce corps, soumis tout entier aux mêmes affections par la similitude de ses parties, touche-t-il quelque objet ou en est-il touché, il en transmet les mouvements à travers tout le corps jusqu’à l’âme et nous procure cette sensation qui nous fait dire que nous voyons. »
Ainsi l’œil humain, selon Platon, est une source active de lumière. Cette conception platonicienne nous donne l’explication la plus claire de la raison pour laquelle dans l’iconographie sacrée égyptienne le Soleil est représenté presque systématiquement comme un œil : parce que, avec toute évidence, les anciens Égyptiens croyaient que le soleil était l’œil d’un dieu qui, bien plus que l’homme, est en mesure d’éclairer le monde .
Mais en peu plus haut nous avons atteint la preuve que ce n’est pas la seule doctrine de l’Égypte ancienne que l’on retrouve dans le Timée. Dans la première partie de cet article , nous avons vu que les anciens Égyptiens connaissaient une certaine version de la théorie de la relativité, qu’ils inscrivirent dans tous leurs lieux sacrés.
Ainsi, il devient historiquement très raisonnable affirmer que l’univers sphérique et absolument uniforme dont parle Platon dans le Timée est celui qui a été inscrit dans les pyramides et les reliefs de l’Ancienne Égypte : il s’agit d’un univers qui résulte d’une contemplation de type mathématique, et non par les perceptions immédiates des sens. Ce n’est pas beaucoup surprenant si
Regarder vers le haut avec sa bouche ouverte ou vers le bas avec sa bouche fermée, il est plus ou moins la même chose jusqu’à ce quenous étudions tout type d’objet perceptible par le sens… La seule véritable façon de regarder vers le haut est d’étudier l’Etre pur, que vous ne pouvez voir du tout.[ Platon , cité par de Santillana ]
6. Nous sommes enclins à attribuer à Platon cette particulière version de l’Ancienne Égypte de la théorie d’Einstein, non seulement parce qu’il semble que les doctrines du Timée font partie du patrimoine de l’Égypte ancienne, mais aussi parce que des idées différentes ne semblent pas être en mesure de clarifier sa conception de l’univers.
Par exemple , Newton a imaginé l’espace absolu comme une sorte, pour ainsi dire, de cube infini, non pas comme une sphère composée d’un nombre infini de centres. En outre, dans la conception newtonienne , les points d’observation ne sont pas équivalents , parce que le seul point de référence que on peut considérer “vrai” est seulement l’espace absolu, et non pas les entités qui s’y meuvent. Par rapport à l’espace absolu, tous les autres points de référence sont à considérer relatifs, c’est-à-dire: les descriptions de l’univers que l’on peut obtenir sont, à proprement parler, fausses et trompeuses.
Au contraire, dans la sphère de Hermès Trismégiste tous les points sont équivalents. Ce qui signifie que par chacun d’eux on peut obtenir une véritable description du cosmos.
Dans la modernité le concept d’un espace comme celui-ci – c’est-à-dire le concept d’un espace comme une sphère absolue – on peut le trouver seulement dans la vision d’Einstein qui, presque sans s’en rendre compte, a construit une théorie quantitative et métaphysique-mathématique telle que l’univers, tout comme la sphère absolue d’Hermès Trismégiste, ne peut pas être correctement défini ni fini ni infini (nous notons en passant que même dans la pensée bouddhiste il y a peut-être allusion à une notion de ce genre dans l’affirmation que le nombre des mondes dans l’univers ne peut être défini ni fini ni infini).
En effet, dans la conception d’Einstein l’univers doit être compris certainement comme un système fini, au moins si l’on pense à la quantité de matière dont il est composé. Mais cette matière se déplace dans un espace où chaque point , puisque il est un point de vue d’égale dignité que tous les autres, peut être considéré comme son centre. Donc, aucun point de cet espace peut être considéré comme son limite. Par conséquent Einstein aurait pu facilement utiliser comme métaphore de sa vision du cosmos les célèbres mots d’Hermès Trismégiste : « l’univers est une sphère dont le centre est partout et dont la surface ne se trouve nulle part. »
7. Pas moins intéressant et proche de notre conception du monde est l’explication que Platon donne de la chute libre. Voyons ce qu’il dit à ce sujet dans le Timée 63
« Placés à la surface de la terre, quand nous mettons dans une balance des substances terrestres et parfois de la terre pure, nous les tirons vers l’air, élément différent, par force et contrairement à leur nature ; alors chacune des deux substances pesées tend à rejoindre sa parente ; mais la plus petite cède plus facilement que la plus grande et suit la première la force qui la jette dans un élément étranger. Aussi l’avons-nous appelée légère, et nous appelons haut le lieu où nous la poussons de force ; dans le cas contraire, nous employons le nom de pesant et de bas. »
Dans un premier temps, un discours de ce genre peut sembler tout à fait naïf et préscientifique. Mais, à bien regarder, les concepts exprimés par Platon sont semblables à ceux que nous pouvons tirer de la loi de Newton, que sur ce point est tout à fait différente de celle d’Einstein. La loi de Newton, dans sa forme mathématique essentielle, nous l’écrivons
F = G [(m1 x m2) : d²]
Si on traduit en mots le sens de cette forme mathématique, nous disons que la masse est attirée par une autre masse, et que plus grandes sont les quantités de masse en jeu plus grande est cette attraction . C’est-à-dire que, comme Platon, nous croyons que le semblable attire le semblable. Et, encore une fois comme Platon, nous croyons que plus la masse est grande, plus cela tend à être attaché à (c’est-à-dire attiré par) une autre masse.
8. Pour être encore plus clairs, nous pouvons citer encore une fois le même passage de Platon que nous venons de citer, en remplaçant le concept et le nom de «terre» avec le nom et la notion de «masse». En ce qui concerne “l’air” , puisque nous ne sommes pas capables de mieux faire , nous allons le remplacer par celui de “vide” (mais il est clair que si avec le mot «terre» Platon fait allusion à un concept très similaire à celui moderne de «masse», avec celui de “air” se réfère plutôt à quelque chose d’autre) . Et nous allons voir que de cette manière le discours de Platon fonctionne encore parfaitement.
« Placés à la surface d’un corps ayant une masse, quand nous mettons dans une balance des substances ayant masse, nous les tirons vers le vide, élément différent, par force et contrairement à leur nature ; alors chacune des deux substances pesées tend à rejoindre sa parente ; mais la plus petite cède plus facilement que la plus grande et suit la première la force qui la jette dans un élément étranger. Aussi l’avons-nous appelée légère, et nous appelons haut le lieu où nous la poussons de force ; dans le cas contraire, nous employons le nom de pesant et de bas. »
Ce sont exactement les concepts que nous enseigne Newton. Le “bas” dans la vue newtonienne, est le centre d’un corps ayant masse. Ce que nous appelons «élevé» est l’espace qui est situé le plus loin de lui. Et plus grande est une masse, et plus grande est la partie de la masse que nous essayons d’en arracher , plus grand est l’effort que nous employons pour faire ce travail. Donc, nous appelons « légers » les corps qui sont composés de peu de masse et «lourds» les corps composés de beaucoup de masse .
Il est vrai cependant que dans sa métaphore Platon n’introduit pas la notion que plus est grande la distance entre deux masses, plus petite est l’attraction que celles exercent entre elles. Cela peut être arrivé, d’une parte, parce que Platon, avec ses doctrines écrites, ne semble s’intéresser presque jamais à clarifier le sens de ses doctrines non écrites. Les doctrines écrites, d’après ce que l’on peut comprendre, ne sont qu’un système complexe et parfois déroutant de métaphores par lesquelles on fait allusion à une connaissance à qui seul les initiés d’un certain niveau peuvent accéder et à qui, dit en passant, semble qu’Aristote n’est jamais arrivé.
En fait , les descriptions de la pensée de Platon données par Aristote ne semblent rien de plus qu’un modèle d’incompréhension et de dépaysement, en particulier en ce qui concerne l’ importance de la géométrie et des mathématiques , qui pour Platon étaient fondamentales, et que, au contraire, Aristote considérait avec ironie et peut-être même avec mépris. Même quand dans le célèbre passage du De Anima Aristote parle de la conception platonicienne de l’âme comme entité à deux dimensions, il ne se rend pas compte que Platon fait allusion à une entité qui peut être décrite au moyen d’un certain type de mathématiques, pas à une entité perceptible par les sens. Comme nous l’avons vu dans la première partie de cet article, même les anciens Égyptiens représentaient des figures humaines à deux dimensions, mais à travers un système complexe de dérivées logarithmiques. Donc, leur conception « bidimensionnelle » de l’âme de l’homme n’était pas, comme on l’a cru jusqu’ici, le résultat de la naïveté d’un esprit rêveur et « mythique », mais d’une science qu’aujourd’hui nous ne sommes pas capables de comprendre.
Donc, il est possible que la raison pour laquelle le concept de la chimie et de la physique qui apparaît dans le Timée est incompréhensible pour nous peut-être est une autre, en plus de la bien connue réticence platonicienne à transférer dans leur totalité les doctrines non écrites dans celles écrites.
Autrement dit, il se peut penser que la physique et la chimie qui – avec Socrate et Pythagore – il avait hérité des doctrines hermétiques égyptiennes antiques étaient structurées de une manière conceptuellement et mathématiquement très différente de celle qui nous est familière dans l’Occident moderne. Si différente que nous ne pouvons pas comprendre ou même imaginer le sens profond des concepts qu’il expose dans le Timée.
9. Très souvent, on a parlé de la doctrine platonicienne des quatre éléments (terre, eau, air, feu) comme d’une sorte de naïveté, ou comme d’un ensemble de superstitions presque inexplicables, liées au monde de la magie. Pour sûr, personne n’a jamais essayé d’expliquer en profondeur les raisons pour lesquelles un homme comme Platon, qui n’était certainement pas un imbécile, a pu se convaincre de la vérité – c’est-à-dire de la «correspondance avec les faits » – d’un certain type de doctrines.
Parce que s’il est vrai que leur sens profond coïncide avec ce qui apparaît aux hommes de notre mentalité et de notre culture, il n’est pas possible de comprendre comment une intelligence telle que celle de Platon n’était pas en mesure de réaliser leur grossière fausseté. Ci-dessous, nous vous proposons un passage dans lequel Platon décrie la chaîne de transformations d’un élément à un autre. Nous avons fait quelques commentaires entre parenthèses pour indiquer au lecteur les éléments problématiques – même seul à un niveau purement psychologique – de l’interprétation traditionnelle de la pensée que Platon a exprimé dans le Timée .
« D’abord nous voyons que ce que nous appelons eau à présent, devient, croyons-nous, en se condensant, des pierres et de la terre (ici aucun commentateur n’a expliqué ou demandé comment il est que Platon, ou, d’ailleurs, n’importe quelle personne raisonnable, aurait pu en venir à croire que l’eau en condensant se transforme en pierre : ici c’est tout à fait clair que l’ « eau » à qui il se réfère n’est pas celle du sens commun ; et cela bien sûr est également valable pour les autres éléments : même, dans un autre endroit , Platon attribue au « feu » l’origine des éléments obscurs), et qu’en fondant et se dissolvant, ce même élément devient souffle et air ; que l’air enflammée devient feu, et qu’au rebours, le feu contracté et éteint revient à la forme d’air (ici on ne comprend d’aucune manière ce qu’il veut dire quand il affirme que le feu, en s’éteignant, revient à la forme d’ air : ce serait comme dire que l’air, en s’allumant, revient à la forme de feu), que l’air condensé et épaissi se transforme en nuage et en brouillard, et que ceux-ci, comprimés encore davantage, donnent de l’eau courante, que l’eau devient de nouveau de la terre et des pierres (personne dans le monde n’a jamais “vu” une chose de ce genre : que de l’eau se forment la terre et le pierres), de sorte que les éléments, à ce qu’il semble, se transmettent en cercle la naissance les uns aux autres. Ainsi, puisque nul d’entre eux ne se montre jamais sous la même figure, duquel d’entre eux pouvons-nous affirmer positivement qu’il est telle ou telle chose et non une autre, sans rougir de nous-mêmes ? Personne ne le peut. »
Timée 48 E, 49 A, B, C.
10. Ici, nous devons comprendre ce que signifient exactement ces propositions, parce que, prises littéralement, elles ne signifient rien. On pourrait dire: Platon pense comme un enfant, il rêve sur les choses et ne les examine pas. Mais les enfants ne disent pas toutes ces choses. Lève la main celui qui a entendu un enfant dire que le feu – en s’éteignant – revient à la forme d’ air! Au contraire, le mode de l’argumentation de Platon semble faire allusion à une connaissance chimique de nature semblable à la nôtre, bien que pas égale. En particulier, peut être que l’ancienne chimie, à laquelle Platon se réfère avec sa doctrine des éléments, non seulement faisait usage de concepts différents, mais pouvait aussi avoir des potentiels différents des nôtres, potentiels que pour l’instant restent totalement inaccessibles. Dans The Snefru Code part. 7 et 8 nous verrons des preuves empiriques qui démontreront de manière irréfutable que dans l’antiquité on était capable de réduire la pierre à l’état pâteux et /ou liquide. Mais si cela est vrai, alors il est possible que un concept comme « condensation » pourrait faire allusion à des phénomènes très différents de ceux auxquels nous faisons allusion avec le même mot.
Par contre, la doctrine platonicienne que toute chose se transforme en toute chose , ne doit pas nous sembler étrange: c’est ce que nous pensons aussi, car nous croyons également que les différentes substances avec lesquelles nous sommes en contact dans la vie de tous les jours, en dépit de leur extraordinaire diversité, en fin de compte se composent et se décomposent en peu des particules élémentaires, les électrons, les protons et les neutrons. Platon avec sa doctrine semble faire allusion à une chose de ce genre.
Peut-être que la terre, l’eau, l’air et le feu , représentés comme corps géométriques, sont seulement une façon schématique de faire allusion à la structure atomique de quatre classes différentes d’éléments que l’on peut obtenir de notre table des éléments. Mais on pourra obtenir la preuve de cette hypothèse seulement par des enquêtes futures qui seront en mesure de trouver des points de communication entre les doctrines scientifiques des anciens Égyptiens et celles que nous avons acquis. Une tâche qui s’annonce difficile, car ces gens avaient une façon d’encoder des données scientifiques, qui, comme nous l’avons vu ci-dessus , n’a pas beaucoup de points communs avec la nôtre, étant donné que ce que nous écrivons sur le papier avec un stylo il le gravaient sur la pierre avec la géométrie.
Horst Bergmann et Frank Rothe ont calculé que la pyramide de Khéops a un volume de près de 2,6 millions de m³, que celle de Khephren arrive à 2,3 millions, et celle de Mykérinos à environ 252 500, pour un total de 5.082.500. Les deux auteurs ne semblent pas avoir remarqué que le premier chiffre correspond plus ou moins à ɸ² x 10⁶ = 2,618033… x 10⁶ = 2618000, et que le total correspond presque exactement à πɸ x 10⁶ = 5,0832 x 10⁶ = 5.083.200.
Pour avoir une idée de ce que pourrait être l’importance d’un nombre comme ɸ dans la science, nous pouvons dire que la vitesse de la lumière peut être obtenue en élevant 10 au 5,476820707 ; 4ɸChéops – 1 = 5,4743. Ou, le rapport entre la masse d’un électron et son rayon est égal à 9,1091/2,81777 = 3,232733 … ; et 2ɸ = 3,23606.
C’est un travail que nous développerons plus profondément dans The Snefru Code part. 7. Mais déjà dans les pages qui suivent, nous avons moyen de nous rendre compte que pour ces personnes, selon toute vraisemblance, sciences comme l’astronomie, la physique et la chimie, n’étaient rien qu’une branche de la géométrie, conçue à son tour comme une branche de la théologie.
troisième partie: UNE ESQUISSE DE LA THÉORIE DES CHAMPS UNIFIÉS PROBABLEMENT CODÉE DANS LA GRANDE PYRAMIDE
1. En 1836-1837 Howard Vyse , pendant une période de recherches intrusives effectuées sur la Grande Pyramide au moyen de la dynamite, a découvert à la sortie du puits d’aréage sud de la Chambre du Roi (celui qui pointe vers la ceinture d’ Orion) une plaque de fer de forme rectangulaire. Elle était d’environ 304,8 mm de long, 101,6 mm de large et avec une épaisseur de 3 millimètres. Et ces dimensions ne semblent pas du tout aléatoires, puisque même à première vue, nous voyons que une proportion de à peu près 3 semble avoir un rôle particulier dans leur détermination.
Donc, nous pouvons essayer – comme essai mental – de reconstruire ses dimensions, à partir des chiffres que par les anciens Égyptiens étaient très importants, en supposant que les mesures ont été prises avec un minimum d’approximation.
Donc , on suppose que l’épaisseur a été déterminée par la formule de 2ɸ ( ou √5 + 1) et que donc elle était initialement 3,23606… mm. Ensuite, nous supposons que la largeur a était déterminée par la formule 2ɸπ x 10 , et que donc elle était originellement 101,66407… mm. En ce qui concerne la longueur, nous supposons qu’elle a été déterminée en utilisant la constante que nous utilisons pour calculer la vitesse de la lumière, qui est égale à 2,9979246. Ainsi, la longueur résulterait de la formule 2ɸπ x 10 x 2,9979246 = 304,7822. La différence par rapport à la mesure de la longueur qui est habituellement acceptée serait ainsi de peu inférieure à deux dixièmes de millimètre.
Si cet essai correspond à la réalité , alors nous aurions que la vitesse de la lumière n’aurait pas été codifiée seulement dans les mesures de la Grande Pyramide, mais même dans cette plaque de fer apparemment anonyme qui avait été placée à l’extrémité du puits d’aréage sud de la Chambre du Roi. Bouval et Hancock ont réalisé des tests sur le métal. Ces tests ont montré que le fer n’était pas d’origine météorique et que, probablement, a été doré. Ce dernier fait est très important par rapport à notre hypothèse, parce que dans l’or nous pouvons envisager un symbole de la lumière, dont la plaque devrait contenir une caractéristique fondamentale.
Nous ne pouvons pas même exclure la possibilité que les autres chiffres qui caractérisent l’objet contenaient d’autres informations scientifique-astronomiques. Le cas du sarcophage de la Chambre du Roi nous a appris que dans des mesures, qui, dans notre culture sont considérées comme triviales, peuvent être contenues des données scientifiques qui étaient importantes pour ces personnes, aussi et surtout parce qu’elles étaient considérées comme directement liées à la création conçue comme un projet d’un divin architecte.
Nous verrons ces choses beaucoup mieux dans la partie 7 du The Snefru Code. Pour l’instant nous nous limitons à un seul exemple, que nous considérons très important. Si nous prenons la longueur de la plaque en décimètres, nous voyons qu’elle est 3,047822. Si nous faisons la relation entre ce nombre et π nous avons que π : 3,047822 = 1,030766, un chiffre qui semble à première vue tout à fait insignifiant.
Que pouvons-nous dire, lorsque nous constatons que le rapport entre le nombre de jours dans une année solaire (365,25) et le nombre de jours dans une année de phases de la lune (354,36) nous donne un nombre à peu près égal à cela, à savoir 1,03073… ? Nous pouvons obtenir un nombre très similaire également par 2ɸ : π = 3,236 … : 3,141 … = 1,030072 … et, naturellement, aussi par ɸ : π/2.
Aussi, en prenant chaque millimètre comme l’équivalent d’un million de kilomètres, nous voyons que la longueur de 304,78 mm correspond presque parfaitement à deux fois la distance maximale entre le Soleil et la Terre, qui est égale à 152,1 millions kilomètres ( x 2 = 304,2 ). Nous pouvons également noter que, en termes de numérologie, il existe une grande similitude entre la distance moyenne entre la Terre et le Soleil et la vitesse de la lumière divisée par deux (149,5978875 contre 1,4989623). Une chose pour nous sans aucune importance, mais qui pour ces personnes aurait pu avoir une signification importante .
2. Rappelons également que le puits d’aréage sud de la Chambre du Roi est celui qui est pointé à la Ceinture d’ Orion. Alnilam , l’étoile centrale et la plus brillante de la Ceinture, est d’environ 1000 années-lumière loin de la Terre. Si on prend chaque dixième de millimètre comme une année-lumière, nous pouvons supposer que la largeur de la plaque (1016 dixièmes de millimètre) représente la distance entre la Terre et Alnilam en années-lumière (soit en termes de temps), tandis que la longueur la représente en termes spatiaux (puisque la longueur est la largeur multipliée par la constante qui donne la vitesse de la lumière).
Il n’est pas impossible que même les dimensions de la Chambre du Roi et de la Reine contiennent des références similaires à Orion et/ou à d’autres étoiles et constellations que pour les anciens Égyptiens étaient très importantes. Par exemple, sa longueur (que nous mesurons le long de l’axe Est-Ouest) est d’environ 10 mètres : si nous prenons chaque dixième de mètre comme symbole d’une année-lumière, nous avons une fois de plus la distance entre la Terre et Alnilam (nous tenons compte que à Gizeh, à l’équinoxe vernal, Orion se lève en direction de l’Est).
D’autres données intéressantes peuvent être obtenues à partir des angles caractéristiques des Pyramides.
L’angle de la base de la Grande Pyramide – en degrés et centièmes de degré – est d’environ 51°, 817, et sur ce sujet on a déjà dit beaucoup de choses. Nous pouvons ajouter que – si nous mettons en relation cet angle avec le nombre de jours des phases lunaires et avec ɸ – de cette opération nous pouvons obtenir une très bonne approximation de la constante que nous nécessitons pour calculer la vitesse de la lumière c, étant donné que
{1 + [ 1:(354,36 : 51°,817)]} x ɸ2 =2,9985192… ≈ c = 2,9979246 (-0,00059)
Ce fait devient encore plus intéressant quand on sait que l’apothème de la Grande Pyramide est d’environ 356,08 mètres. Toutefois, ce calcul suppose que les côtés de la Pyramide sont parfaitement droits. Mais, au lieu de cela, ils forment une légère queue d’aronde vers l’intérieur. Cela signifie que l’ apothème est de longueur légèrement inférieure à celle qui est calculée à partir de la hauteur et de la longueur d’un côté. Et il ne serait pas surprenant si sa mesure coïncidât presque exactement avec le nombre de jours de l’année de phases lunaires.
L’inclinaison de la Pyramide de Khephren est de 53°, 167. Le nombre exact de jours dans une année solaire (365,25) divisé par cette inclinaison nous donne 6,8698 .., un chiffre qui est très similaire à ɸ4 = 6,8541. Au lieu de cela , en utilisant la longueur de l’année lunaire nous avons 354,36 : 53°, 167 = 6,6650365 … un chiffre qui est très proche de la constante de Newton (6,67 ) et que au niveau numérologique nous rappelle le biblique Nombre de la Bête, le 666 (qui pourrait donc être un moyen de faire allusion à la constante de Newton).
Ce nombre a été symbolisé avec l’architecture aussi à Teotihuacan. Dans « Fingerprints of the Gods » Hancock parle d’un effet lumineux qui se produit aux équinoxes
« Puis , à midi, le passage des rayons du soleil du sud au nord a provoqué l’ effacement progressif d’une ombre parfaitement droite qui longeait un des ordres inférieurs de la façade occidentale. L’ensemble du processus, de l’ombre totale à l’illumination totale, a été réalisé exactement en 66,6 secondes » .
Mais si on utilise l’Année des Eclipses, alors nous avons 346,6 :53°,133 = 6,52… un chiffre très proche de la constante de Planck calculée en erg par seconde (correspondant à 6,55 ; celle en joule correspond à 6,626). En outre, il est à noter que l’angle de base de la Pyramide de Khephren est très similaire à l’angle opposé au côté majeur du triangle rectangle avec côtés de 3 et de 4 et hypoténuse de 5, qui a un sinus de 0,8 et est égale à 53°,13.
Mais si nous modifions d’une façon minime les mesures canoniques de la célèbre triade pythagoricienne, on peut imaginer que les proportions de la Pyramide de Khephren correspondent à 2,9979246 (c’est-à-dire « c »), 4 et 4,998755 (la mesure de l’hypoténuse que résulte de deux côtés). L’angle qui en résulte serait 53°,149. De cette façon les Anciens Égyptiens auraient trouvé moyen de coder architectoniquement la vitesse de la lumière en utilisant une approximation presque parfaite d’une triade pythagoricienne fondamentale. Il convient aussi noter que l’utilisation de π au lieu de 3 conduirait à un angle de 51°85, très proche de celui de la Grande Pyramide, qui est égal à 51°,517.
L’angle de base de la Pyramide Rhomboïdale est d’environ 54 ° 30′. Si on divise les 360 jours « purs » du calendrier égyptien par cet angle, nous avons que 360 : 54,31 = 6,628 … qui est une bonne approximation de la constante de Planck. Et, si nous ajoutons le sinus et le cosinus de cet angle, nous avons la racine cubique du nombre d’Euler (3√e = 1,3956..).
Nous trouvons ce nombre codifié aussi dans les mesures de la Grande Pyramide, puisque le côté est de 440 coudées et 440 : 2,71828 = 161,8670629957179. En divisant ce nombre par 100, nous obtenons 1,61867062. Mais le nombre d’or est 1,618033… , et l’approximation au nombre d’or qu’on peut déduire à partir des mesures de la Grande Pyramide est égale à 1,61859…
Si maintenant on transforme numérologiquement l’angle de 54°30’, calculé en degrés et en soixantièmes de degré en celui calculé en degrés et en centièmes de degré, nous avons un angle égal à 54°,5. Si on divise ce chiffre par 1000 et y ajoutons 1, nous avons 1+ (54,5 :1000) = 1+0,0545 = 1,0545 = ħ = 1,054571, où ħ est la variante de la constante de Planck mise au point par Dirac.
L’angle de la base de la pyramide de Mykérinos est de 51°,367 . La tangente de cet angle est égale à 1,2511, un nombre très similaire à √π/2 = 1,25331 . … ( Si la tangente est égale à √π/2 l’angle est de 51°,4141).
L’angle de la base de la Pyramide Rouge est d’environ 43°35. Multiplié par 2 il nous donne un angle pratiquement identique à 86°,7812… : dans ce cas, la somme des sinus et cosinus nous donne 1,054571 … , qui est la valeur de ħ, une variante de la constante de Planck développée par Dirac.
Une très bonne approximation de ce nombre est la somme de sinus, cosinus et tangente d’un angle égal à π/2 ; le résultat de cette somme est 1,054458… ; en utilisant la valeur de π que l’on retrouve dans la Grande Pyramide (22/7) , le résultat est 1,054480… : de cette manière, nous découvrons que deux données empiriques – qui nous avons la tendance à juger contingentes et non plus explicables – l’erreur minimale possible dans la détermination de la position et de la vitesse d’une particule et le quantum d’action – sont tous les deux contenus dans une valeur géométrique fondamentale que jusqu’à présent on croyait totalement abstraite et déconnectée de la réalité empirique, puisque nous avons que (tangente π/2 + cosinus π/2 + sinus π/2) x 2π = h, la constante de Planck. Cela signifie, par exemple, que la formule pour déduire le nombre quantique principal (n) que nous écrivons n x h/2π après que nous l’avons dérivée au moyen d’une recherche empirique laborieuse, aurait pu être dérivée avec une procédure a priori menée exclusivement par des bases trigonométriques.
Cette étrange affirmation devient plus convaincante quand nous constatons que, aussi étrange que cela puisse paraître, nous pouvons obtenir une valeur remarquablement proche de h – la constant de Planck – en divisant 360° avec l’angle de 54°,3718624 , qui a pour principale caractéristique que soustrayant le sinus et le cosinus de la tangente, on obtient zéro. Symboliquement, cela semble un fait très important : il est comme si dans la trigonométrie était inscrit le fait empirique que, sous une certaine quantité, l’émission d’énergie est impossible (on notera au passage que l’angle au sommet de la Grande Pyramide est remarquablement proche du double de l’angle de 38°,1727…, qui est caractérisé en ce que la différence entre la tangente et le cosinus est égal à 0, alors que le sinus est égal à 1/ɸ) :
360° : 54°,3718624… = 6,62107… (la constante de Planck est calculé actuellement égale à 6,62559…).
Si l’on multiplie ce même angle par (1/ɸ x π²) + 1/ɸ nous avons que 54°,3718624… x 6,7177.. = 365,2584 …, , c’est à dire la durée exacte d’une année solaire.
Au lieu de cela , si l’on divise la longueur de l’année solaire par cette approximation a h, nous avons que 365,25 : 6,62107… = 55,164799… ; si nous faisons la somme de sinus, cosinus et tangente d’un angle comme cela, nous arrivons à un résultat de 2,8289… , un nombre qui est pratiquement identique à 2√2.
Un nombre pratiquement identique à la √2 résulte aussi de la tangente de l’ angle qui résulte de la relation entre la longueur de l’année solaire et la constante de gravitation, étant donné que 365,25 : 6,673 … = 54°, 736…, un angle dont la tangente est égale à 1,41425… (√2 = 1,41421…).
3. Il semble donc que la plaque trouvée par le colonel Vyse, loin d’être un objet banal, pourrait contenir d’importants concepts scientifiques, qui atteignent des niveaux inimaginables de sophistication.
De la face plus grande de la plaque, on peut créer deux triangles rectangles dont l’hypoténuse coïncide avec la diagonale du rectangle. L’angle opposé du côté mineur est de 71°,5531526028, dont la tangente est égale à 2,9979245999… : ce chiffre est presque exactement le même de la constante à partir de laquelle nous pouvons calculer la vitesse de la lumière, qui, comme nous l’avons vu , est égale à 2,9979246.
Mais l’angle le plus intéressant est certainement celui de 66°,2699, à partir duquel nous pouvons encore une fois obtenir une valeur presque identique à “c” en multipliant tg x (sin + cos) = 2,9979222 … Ici, la chose importante à noter est que on peut construire numérologiquement cet angle avec une bonne approximation par le produit h x 10 = 6,62599 x 10 = 66,2599 (la différence est d’un dixième de degré) . Ce particulier crée un lien profond avec le solide que nous avons vu ci-dessus.
En fait, en reprenant l’analyse de la plaque qui se trouve au fond du puits d’aération Sud de la Chambre du Roi, si l’on multiplie le cosinus de 71, 55315 (0,3164.., un chiffre plus ou moins égal à √10) et puis nous faisons 1/x , nous obtenons 1,054165 … , un nombre qui correspond presque parfaitement à ħ, la valeur qui remplace souvent “h” constante de Planck (ħ= h/2π = 1,054571). Naturellement, nous pouvons obtenir une valeur égale en divisant l’hypoténuse pour le côté plus grand, puisque 321,289… : 304,781… = 1,05416554, avec une différence par rapport à la valeur de notre constante d’environ 3 dix-millièmes.
Cette valeur peut être obtenue avec une bonne approximation aussi de 130√103 = 1,054573667 … ; et en divisant l’exposant de la racine par celui de la puissance nous avons 130 : 3 = 43,333 … , qui est l’angle de base de la Pyramide Rouge exprimé en degrés et soixantièmes de degré ; le réciproque de cet angle sur un quart de tour (90°) a une tangente de 1,05378, un nombre de nouveau très proche de ħ (l’angle avec la tangente identique à ħ est celui de 46°, 52 ; la somme de sinus et cosinus de cet angle est presque identique à √2)) . Il faut aussi noter que l’angle de base de la Pyramide Rouge correspond à une bonne approximation de la valeur de la constante qui est utilisée pour calculer la surface de l’icosaèdre (5√3 = 8,66 … = 10 x sin 60°) multiplié par 5 , étant donné que 8,66 .. x 5 = 43,301 .
Encore, si l’on divise l’angle plein pour angle avec la tangent égale a c multiplié par π , nous avons que 360 (71°,55315… x π ) = 1,601488 … , une valeur qui est remarquablement proche de la valeur mesurée en joules d’un électronvolt (1,60217653) et pratiquement identique à l’ approximation du nombre d’ or qui on trouve dans la Pyramide de Mykérinos.
L’angle de 71°,5531526028 , à un niveau numérologique est très similaire à la durée en années d’un Jour de précession, résultant de la division des 26.000 ans d’une Année de précession en 365 parties au lieu des connus 360 (le résultat est égal à 71,2328). Un angle très similaire résulte également de la relation entre le quart de l’angle plein et la racine cubique de deux, étant donné que 90 ° : ³√2 = 71 °,433. Multiplié par π ce même angle il donne un résultat de 223 °,78468217351, un chiffre qui est très similaire à la section d’or de l’angle plein (222,49).
Par contre, le produit de la valeur exacte de ħ par la constante dont on obtient la vitesse de la lumière nous donne un résultat égal à 3,1615243433466. Cette valeur correspond à la tangente d’un angle de 72 °,4476, ce qui au niveau numérologique correspond presque parfaitement à au nombre d’années solaires qui dure une journée de précession canonique, égal à 26000 : 360 = 72,2222. Ou, également à 90° :ᴾᶦ√2 = 72°,180799 (curieusement, la racine cinquième de 360 nous donne un résultat de ⁵√360 = 3,24534, très semblable à 2ɸ, qui correspond à l’épaisseur de la planche ; par contre, la racine-π de la durée exacte d’une année solaire est égale à ᴾᶦ√365,25 = 6,5418, un nombre très similaire à la valeur de “h” calculée en ergs par seconde (le nombre réel est 6,55 ; nous rappelons que 10 élevé à 3,1646… nous donne 1461, c’est-à-dire la durée du cycle de Sirius : la coïncidence au niveau numérologique avec le volume de l’Arche (une chose que nous allons voir dans un instant) semble donc raisonnablement significative , et encore plus significative nous semblera si l’on note que ħ x 3.1646 x 2 = 6,67461 … , c’est-à-dire une remarquable approximation de G, la constante gravitationnelle élaborée par Newton)).
Le cycle solaire annuel et celui de la précession représentent un élément de l’unicité, presque les empreintes digitales de la Terre par rapport aux autres entités astronomiques qui se déplacent dans l’univers. Mais dans le nombre de ces cycles, ce semble , sont codifiées les constantes de nos lois scientifiques les plus importantes. Ainsi, les anciens calendriers contiennent probablement, même si de façon hermétique, les nombres fondamentaux de toutes les lois fondamentales de la physique.
Nous allons discuter plus profondément ces sujets dans The Snefru Code part. 4 et 7. Ici nous nous limitons à un seul exemple. Pi grec – la constante qui est utilisée pour déterminer le cercle et, comme nous l’avons vu plus haut, même la constante de Planck – avec ɸ est contenue dans les cycles cosmiques fondamentaux qui regardent la Terre. Cela signifie que des faits empiriques contiennent les nombres fondamentaux des lois de la physique qui les décrivent . Par exemple, la tangente égale à π est caractéristique de l’angle de 72°34…, un angle que en termes de numérologie est pratiquement identique à cette unité de temps, essentielle pour les anciens, qui était le Jour de précession (qui est égal à 72,2222 années solaires). Mais dans π, comme nous l’avons vu , sont contenus les deux nombres fondamentaux de la mécanique quantique.
Donc, nous aurions découvert ce que Platon voulait dire quand il a dit dans le Timée que « la terre, notre nourrice, tourne autour de l’axe qui traverse tout l’univers ». Avec ces mots , Platon ne veut pas dire, comme on a cru, que l’univers tourne autour de la Terre, mais que les nombres fondamentaux qui sont contenus dans les cycles cosmiques terrestres – dans lesquels sont à leur tour contenus les nombres de ces lois fondamentales de la physique et des mathématiques – sont la forme logique de tout ce qui peut arriver dans l’univers.
4. En fait , cette thèse platonicienne semble avoir vraiment quelque fondement. Au-delà de ce que nous avons déjà dit, nous pouvons ajouter que la relation que nous avons vu ci-dessus entre la constante de Newton (G) et celle Planck (h) semble en partie contenir et en partie faire allusion à des relations harmonieuses entre le monde abstrait des théories géométriques et les mesures empiriques des cycles astronomiques de la Terre. Par exemple (G/h)⁸ = 1,054897…, c’est-à-dire un chiffre très près de ħ, élevé à la 72ème puissance (il faut se rappeler que le 72 est un nombre/mesure du cycle de précession typique et extrêmement important) nous donne (G/h)⁷² = 1,617677… , un nombre qui diffère de moins de 3 dix-millièmes du nombre d’or.
Cette relation semble avoir un poids dans le rapport qui semble exister entre d’autres constantes physiques qui regardent la structure de l’atome.
Par exemple, le rayon classique du proton est égal à 1,535 x 10-18 m, alors que celui de l’électron est 2,8179403267 x 10- 15 m . Le rapport de ces longueurs (à l’exclusion des puissances de 10) est égal à 1,535 : 2,817940367 = 0,54472408 …. Ce nombre – élevé au cube – est 0,161632…, une valeur très proche de ɸ : 10. Par contre, multiplié par deux et ensuite élevé à la sixième puissance nous donne (0,54472408… x 2)⁶ = 1,08944817…⁶ = 1,67201227…, qui est une valeur remarquablement similaire à celle de la constante utilisée pour calculer la masse au repos du proton, qui est égale à 1,6726231.
On notera en passant que cette valeur peut être reconstruite même par moyens cosmologiques-numérologiques. Osiris – Orion disparaissait de l’horizon pour environ 70 jours et si nous divisons les jours « purs » du calendrier égyptien par ces 70 jours on obtient une valeur de 5 + 1/7. Si l’on divise 70 par 5 + 1/7 on obtient 13,6111… Si l’on divise 5 + 1/7 par 13,6111… nous arrivons enfin à 0,377842 …, une valeur qui multipliée par π et élevée à la troisième puissance nous amène à 1,672562, une valeur très proche de celle de la constante utilisée pour calculer la masse au repos du proton.
Si l’on divise la relation entre la constante de Newton G et celle de Planck h par le nombre que nous avons obtenu nous avons que (6,67 : 6,62559) : 1,67201227 = 1,006702 … : 1,67201227 = 0,60209… En ajutant 1, cette valeur correspond à la charge électrique du proton, comme 1,602 – 1 = 0,602 (1/0,602 = 1,6608…, un nombre très proche à la constante qui sert pour transformer les soixantièmes de degré en centièmes de degré).
Une relation similaire existe aussi entre le moment magnétique du proton 2,793 et sa masse au repos, car 1,6726231 : 2,793 = 0,598862 (la différence avec la charge électrique cette fois est d’environ 1 + 3.14 millièmes (donc très près de 1 + π/1000)).
Ci-dessus , nous avons vu que la masse d’un électron est d’environ 1/1836 fois celle du proton. Si l’on fait le rapport entre le rayon classique du proton et celui de l’électron, on voit que
2,8179403267 x 10 – 15 : 1,535 x 10-18 = 1,8357917… x 103 = 1835,7917..
Par conséquent, il semble que au niveau atomique la masse soit inversement proportionnelle à l’espace occupé par la charge électrique, étant donné que le rayon classique du proton est d’environ 1/1836 fois celui de l’électron. De cela, nous pouvons déduire que peut-être la masse (et donc le champ gravitationnel exprimé par la masse) n’est que – pour ainsi dire – énergie magnétique concentrée. Donc, hypothétiquement, si on pouvait concentrer la charge de l’électron dans un rayon classique équivalent à celui du proton, nous pourrions augmenter sa masse en proportion. A l’inverse, l’expansion de l’espace occupé par la charge électrique du proton réduirait la masse (et donc son poids) à une valeur proche de celle de l’électron. Et cela pourrait être justement la manière par laquelle dans les temps anciens on a pu déplacer ces blocs de granit monstrueux, pesant plus d’un millier de tonnes , qui nous ne serions pas en mesure de déplacer même en utilisant notre technique la plus avancée. En outre, il est possible que cette opération puisse créer un déséquilibre chimique- magnétique de telle sorte que les matériaux plus durs puissent être réduits à un état pâteux. Cela expliquerait l’extraordinaire facilité avec laquelle des gens comme les anciens Égyptiens pouvaient travailler des pierres comme la diorite avec la même facilité que nous travaillons la plastique ou l’aluminium (et ici nous trouvons aussi un indice de ce que Platon pourrait entendre avec un terme comme «condensation»).
Si cette hypothèse correspond à la réalité, il serait possible de construire des dynamos qui tournent en utilisant ce que l’on pourrait appeler une sorte de « volant gravitationnel », qui pourrait fonctionner sans l’aide de l’électricité produite par les centrales électriques, qui nécessitent l’utilisation des mines de charbon, ou des puits de pétrole, des réseaux de transmission de haute tension, etc. Ce qui expliquerait pourquoi les constructeurs des pyramides pourraient avoir accès à l’énergie sans la nécessité de tous ces équipements dont nous avons besoin dans notre temps.
En outre, étant donné que le champ de gravitation est généré à partir des charges opposées, son action peut à son tour être alternativement positive ou négative alors qu’il s’étend dans l’espace en forme d’ onde. Cela pourrait signifier que l’univers peut s’étendre et se contracter dans un certain intervalle de temps et d’ espace sans jamais parvenir à la mort thermique et sans que sa phase actuelle d’expansion doive être expliqué par une explosion originaire.
5. Nous notons en passant que, si électrons et protons peuvent être considérés comme des sphères, alors l’électron aurait un volume de plus de six milliards de fois plus grand que le proton , étant donné que l’électron a un rayon d’environ 1835,791 fois supérieur à celui du proton ; cela veut dire que son volume serait 1835,791 … ³ = 6186859530, un nombre qui est très proche de 1/ɸ x 1010 . Nous ne pouvons pas manquer de remarquer que la constante qui est utilisé pour déterminer la relation entre la force de gravitation et le champ magnétique exprimé par un électron, est d’environ 4,17 , un nombre aussi très proche du rapport entre les valeurs constantes qui servent à déterminer le volume du cercle, étant donné que 4/3 π = 4.188… : compte tenu de la petitesse des mesures en jeu, il n’est pas exclu que la valeur déterminée géométriquement peut être plus précise que celle déterminée empiriquement.
Mais cela ne semble pas le cas, parce que si nous faisons la proportion entre la relation qui existe entre la force magnétique et la force gravitationnelle exprimées par un proton et celle d’un électron, nous nous rendons compte que le résultat est déterminé par une valeur proche de 1835,791… au carré , et non au cube
4,17 x 1042 : 1,24 x 1036 = 3.362.903,2258
Si nous faisons la racine carrée de ce nombre , nous voyons que
√3.362.903,2258 = 1833,822…
Considérant les petites erreurs qui peuvent y avoir dans la détermination des constantes, nous pouvons penser que ce rapport correspond à 1835.791…2. Cela pourrait signifier que l’électron et le proton doivent être considérés comme des cercles, et non comme des sphères, et, à son tour, cela pourrait signifier que les théories scientifiques modernes qui tiennent compte de la troisième dimension – c’est-à-dire de la profondeur – et sont considérées comme une illusion auraient trouvé un autre fondement. Ce serait aussi la signification profonde de l’adoption de la représentation en deux dimensions de la part des anciens Égyptiens.
En outre, si nous faisons la relation entre le rayon classique de l’électron et celui du proton à l’exclusion des puissances de dix, nous obtenons un autre résultat intéressant car
2,8179403267 : 1,535 = 1,8357917437785016286644951140065
Si nous faisons le rapport entre ce nombre et la charge électrique de l’électron et du proton , on voit que
1,835791… : 1,60217653 … = 1,14581…
Ce nombre semble être extrêmement important, car il est pratiquement identique à 1 + 1/ɸ4. En effet
1 + 1/ɸ4 = 1 + 0,145898.. = 1,145898…
Comme on peut le voir, la différence est d’environ 8 x 10-5 ( curieusement , 8 et 5 sont le sixième et le cinquième chiffre de la série de Fibonacci et leur produit nous donne le 40 que l’on trouve très souvent dans l’Ancien Testament : et en multipliant les 40 jours pour les 40 nuits du déluge biblique nous arrivons à 1600, un nombre très similaire à ɸ multiplié par 1000, dont la racine est 40,22).
A ce résultat nous pouvons ajouter les autres que nous avons trouvés avant. Avec l’exclusion des puissances de 10, si nous faisons la relation inverse entre le rayon du proton et celui de l’électron, nous constatons que
1,535 : 2,817940367 = 0,54472408….
Ce nombre – élevé au cube – est 0,161632…, une valeur très similaire à ɸ/10 (en fait 3√ (ɸ/10) = 3√0,1618033988… = 0,544915…, la différence avec la valeur calculée ci-dessus est de 21 dix-millièmes).
Au lieu de cela, multiplié par 2, et puis élevé à la sixième puissance nous avons
(0,54472408… x 2)⁶ = 1,08944817…⁶ = 1,67201227…..
C’est-à-dire, une valeur remarquablement similaire à celle de la constante utilisée pour calculer la masse au repos du proton qui est égale à 1,6726231.
Compte tenu des petites erreurs dans la détermination du rayon classique du proton et de l’électron nous pouvons supposer que les valeurs des nouvelles constantes correspondent parfaitement à 1 + 1/ɸ5 et √(ɸ/10). Ce fait peut expliquer pourquoi les anciens Égyptiens tenaient tellement à coder le ɸ et le π dans la Grande Pyramide , car avec ces deux nombres on peut décrire la forme logique-physique et géométrique-mathématique de tous les événements qui se produisent dans le monde .
6. La connexion du rapport inverse entre le rayon classique de l’électron et du proton et leur masse avec le reste de leurs propriétés physiques est complétée par la découverte , maintenant pas trop surprenante, que cette relation semble se faire sentir même dans la distance moyenne entre la première orbite et le noyau de l’atome d’hydrogène, qui correspond à 0,53 x 10-10 m. En effet, si on fait le rapport de cette distance avec le rayon classique de l’électron, on voit que
0,53 x 10-10 : 2,8179403267 x 10- 15 =
= 0,000000000053 : 0,0000000000000028179403267 = 18808,0632…
Si nous faisons la même opération avec le rayon classique du proton nous arrivons à ce résultat
0,53 x 10-10 : 1,535 × 10-18 =
= 0,000000000053 : 0,000000000000000001535 = 34527687,2964
Si l’on divise ce nombre par ce que nous avons obtenu par rapport à l’électron nous avons que
34527687,296416938110749185667752 : 18808,0632 = 1835,791
Autrement dit, nous retrouvons la relation inverse qui existe entre le rayon classique et la masse de l’électron et du proton .
Si l’on divise par 10 la valeur relative au proton et ensuite nous faisons la racine nous avons que
√34527687,296… : 10 = √3452768,7296… = 1858,162729
Ce nombre pourrait revêtir une signification, car il semble faire allusion à un rapport mystérieux entre le rayon de la première orbite et celui du proton et de l’électron, correspondant à une autre mystérieuse valeur constante. En fait, si l’on divise la valeur de l’électron par 10 et puis on fait la proportion on constate que
18808,0632/10 : 1858,162729 = 1880,0632 : 1858,162729 = 1,0121860104…
1858,162729 : 1835,791… = 1,012186.4248…
1835,791… x 1,012186…2 = 1880,80628…
Ce nombre (1,012186) correspond de façon assez précise à la relation entre h mesuré en joules (6,626) et en ergs (6,55), étant donné que 6,62559 : 1,012186 = 6,5458. Nous savons aussi que les distances entre les orbites des électrons et du noyau sont intimement liées à leur état d’énergie, à son tour connecté avec le nombre quantique principal. En outre, la division par 10 de la valeur relative de l’électron pourrait être en quelque sorte à l’origine d’un système de mesure décimale de l’ancienne Égypte (ce qui pourrait être à son tour la cause de notre propre système).
Il semble donc que entre l’espace et l’état de l’énergie il y ait, à l’échelle microscopique , une intime connexion, semblable à cette que nous trouvons entre la masse et l’énergie dans la relativité générale.
La théorie des champs unifiés de l’ancienne Égypte serait donc, pour ainsi dire, une sorte de généralisation de la relativité générale dans laquelle l’espace, compris comme le rapport entre le rayon classique de l’électron et du proton, entre dans la définition de la masse, de la charge, de la distance entre les orbites et vice versa.
Que les anciens Égyptiens étaient arrivés à une conception de ce genre est une possibilité à considérer non seulement à cause de tout ce que nous avons vu dans la première partie de l’article, mais aussi par ces nouvelles découvertes . Si nous faisons égal à 1 le rayon classique de l’électron, nous avons que le proton est de 1/1835,791 cette mesure. Si nous arrondissons ce nombre au chiffre supérieur (1836), puis nous faisons la division par un des deux nombres typiques du cycle de Sirius nous avons que
1836 : 1460 = 1,257534..
Si nous prenons ce résultat, l’élevons au carré et le multiplions par 2 , nous avons que
1,257534..2 x 2 = 3,162784762….
Ce nombre est très proche du cosinus multiplié par 10 de cet angle de 71°,5531526028 – ce que nous avons vu ci-dessus – dont la tangente est égale à c = 2,9979246…, c’est-à-dire pratiquement identique à la constante de laquelle on obtient la vitesse de la lumière. Il faut aussi se rappeler que en multipliant le cosinus de cet angle (0,316424 … ) par la tangente et puis en faisant 1/x avec le résultat, nous avions obtenu un nombre égal à 1,054165… , qui correspond presque parfaitement à ħ, la valeur avec laquelle très souvent on remplace “h” constante de Planck ( ħ = h/2π = 1,054571)
Mais cette valeur peut être obtenue avec une bonne approximation aussi de 130√103 = 1,054573667. En ce cas si nous divisons l’exposant de la racine à celle de la puissance nous avons que 130 : 3 = 43,333 … , qui est l’angle de base de la pyramide Rouge exprimé en degrés et soixantièmes de degré ; l’angle complémentaire de 43°,333 sur un quart de tour (90°) a une tangente de 1,05378, un nombre de nouveau très proche de ħ (l’angle avec la tangente exactement égale à ħ est celle de 46°,52 ; la somme de sinus et cosinus de cet angle est presque identique à √2)).
Considérant qu’une meilleure approximation a cette valeur nous la pouvons dériver en additionnant sinus, cosinus et tangente d’un angle égal à π/2 , nous pouvons dire que, dans en certain sens, nous avons démontré que entre la géométrie et la réalité il n’y a aucune différence . Tous les résultats auxquels notre science est arrivée par une longue et dure recherche empirique pourraient être déduits de spéculations géométriques réalisées de manière complètement a priori. Qui sait, peut-être ne soit pas celle-ci la raison pour laquelle Platon a donné tant d’importance à la géométrie.
Ce serait aussi la démonstration que l’idée de Kant avant et après de Wittgenstein – c’est-à-dire que les vérités mathématiques sont des tautologies, et que d’elles nous ne pouvons pas obtenir aucune information sur le monde empirique – est complètement fausse. Si tel était vraiment le cas, l’idée de la Bible que le monde a été créé par Dieu, « selon nombre et mesure » serait confirmée. Au contraire serait falsifiée l’idée répandue dans les temps modernes, que le monde a été formé par hasard.
7. En fait, si nous essayons de résumer et mettre un peu d’ordre dans les résultats obtenus au cours de cette peut-être un peu trop tortueuse recherche, nous voyons qu’ils sont tout à fait intéressants. Tout d’abord, nous voyons en succession les valeurs du rayon classique et de la masse de l’électron et du proton
masse au repos de l’électron me = 9,1091*10-31 kg
masse au repos du proton mp = 1,6725*10-27 kg
rayon classique de l’électron re = 2,81777*10-15 m
rayon classique du proton rp = 1,535 × 10-18 m
Comme nous l’avons déjà vu, au moins en partie, les relations que nous construisons à partir de ces valeurs semblent très significatives. Et elles semblent encore plus significatives quand nous nous rendons compte qu’elles, en excluant les puissances du 10, correspondent presque parfaitement à des relations entre π et ɸ
me/re = 9,1091 : 2,81777 = 3,23273.. ≈ 2ɸ = 3,23606…
mp/rp = 1,6725 : 1,535 = 1,089576… ≈ (2ɸ/π)3 = 1,092957…
Mais (2ɸ/π) correspond presque parfaitement au rapport entre le nombre de jours de l’année solaire avec celui de les phases lunaires, étant donné que 365,25 : 354,36 = 1,0307314 .. et 2ɸ/π = 1,030072. La différence entre la valeur qui sort de mp/rp est vraiment négligeable. En fait, nous voyons que, restant presque identique le rapport , puisque me/re ≈ 2ɸ , la relation avec 3√mp/rp devrait nous donner un nombre très proche de π. En fait nous voyons que
3√mp/rp = 3√1,089576… = 1,029009…
(me/re)/ 3√(mp/rp) = 3,23273…. : 1,029009… = 3,141598492…. ≈ π (il faut se rappeler que 1/π = 0,318309.. ; si nous interprétons cette valeur comme un sinus, nous voyons que ce sinus est celui de l’angle de 71°,439.. ; le sinus de 71°,439.. est égal à 0,94798… et 1/0,94798… = 1,054867, c’est-a-dire un nombre encore une fois très proche de ħ = 1,054571…)
La différence avec π n’est finalement pas plus grande d’environ 6 x 10- 6. À ce stade , personne ne sera particulièrement surpris même si la constante que nous nécessitons pour calculer le rayon de la première orbite de l’électron autour du noyau de l’atome d’hydrogène (la constante de Bohr) peut être dérivée avec une bonne approximation par une fonction de ɸ. La valeur de ce rayon est en effet de 0,53 x 10-10 m . Nous pouvons obtenir la valeur de la constante de cette façon
1/(1 + 1/ɸ3)3 = 0,529508…
Ainsi , si la longueur d’onde est λ = 2πr/n , où n est la série des nombres naturels, nous pouvons maintenant obtenir la valeur de λ au moyen d’une fonction de π et ɸ , de sorte que nous pouvons écrire
λ = 2π [1/(1 + 1/ɸ3)3] /n
8. Ces rapports ont des conséquences évidentes sur les équations dans lesquelles ils sont placés en relation avec les valeurs dynamiques des particules élémentaires. D’après ce que nous avons vu plus haut , la masse de l’électron peut être dérivée à partir de son rayon avec la simple équation
me/re = 9,1091 : 2,81777 = 3,23273… ≈ 2ɸ
nous avons ainsi que
me = re 2ɸ
De cette façon, la fameuse équation sur la longueur d’onde de l’électron de De Broglie que nous voyons ci-dessous
λ/v = h/me
pourrait être ainsi transformée
λ/v = h/me = (sinus π/2° + cosinus π/2° + tangente π/2°) x 2π/re x 2ɸ
Mais si nous faisons le rayon de l’électron égal à 1 (c’est-à-dire , si nous le considérons comme une unité de mesure) , nous voyons que l’équation devient une simple fonction de π et ɸ
λv = h/me = (sinus π/2° + cosinus π/2° + tangente π/2°) x 2π/2ɸ
Ci-dessus , nous avons vu que λ = 2π [1/(1 + 1/ɸ3)3] /n. Cela signifie que cette formule peut être ainsi transformée
{2π [1/(1 + 1/ɸ3)3] /n} v = (sin π/2° + cos π/2° + tg π/2°) x 2π/2ɸ
Par conséquent, nous avons que ν est égal à
ν = [(sinus π/2° + cosinus π/2° + tg π/2°) x 2π] : 2ɸ {2π [1/(1 + 1/ɸ3)3] /n}
Ou , le célèbre principe d’incertitude développé par Heisenberg deviendrait
Δx Δp ≥ 1/2 ħ = Δx Δp ≥ 1/2 sinus π/2° + cosinus π/2° + tangente π/2°
ou bien
Δx Δp ≥ 1/2 ħ = Δx Δp ≥ 1/2 9√ɸ
Par un tel processus , nous pouvons déduire la constante ( 1,535 ), dont nous avons besoin pour déterminer le rayon du proton, et le rapport ( 1,83591 x 103) avec celui de l’électron . Nous allons commencer à nouveau à partir de π , mais dans l’approximation que l’on trouve dans la Grande Pyramide , qui est la multiplication de fraction 22/7
rp = (πChéops : 2) : {1 + [(1: ɸ3) : 10]} = (3,142857… : 2) : {1 + [1/0,618033…3] : 10]} =
= 1,57142857… : [1 + (0,23606… : 10] = 1,57142857… : 1,023606… = 1,53518…
La constante de la masse peut être obtenue à partir du diamètre classique, divisé par la constante (1,835791) qui indique que la masse est inversement proportionnelle aux dimensions du rayon
dp = (rp x 2) = 1,535 x 2 = 3,07 (Notez que nous pourrions obtenir une bonne approximation de ce chiffre aussi de 2ɸCheops : 4√[1 + (ɸCheops – 1)3 = 3,23718 : 4√[1 + 0,618593) = 3,23718 : 4√1,2367.. = 3,23718 : 1,054548.. = 3,06973)
3,07 : 1,835791 = 1,6725 mp
Nous pouvons dériver la charge du proton et de l’électron en divisant cette constante (1,835791) par 1 + 1/ɸ4
1,835791 : (1 + 1/ɸ4) = 1,6020….
Deux moyens possibles pour dériver la constante égale à 1,835791 sont ceux qui nous voyons ci-dessous
3√(1/ɸ x 1010) : 103 = 1,835146..
Or , en utilisant une approximation très précise de π (3,1438, qui diffère de la valeur réelle de π de moins de 3 millièmes), on peut écrire
103,1438 + 103,1438/3,1438 = 1835,45557…
Avec la valeur réelle de π cette même équation nous donne la valeur suivante
10π + 10π/π = 1385,455 + 441,004 = 1826,45998
Il semble également assez important que la relation entre le rayon du proton et de l’électron nous donne un résultat très intéressant même si on le rapporte numérologiquement à l’angle de 360° (et donc aussi au nombre de jours «purs» dans le calendrier Maya et de l’ancienne Égypte
1835,791 : 360 = 5,0994 ≈ πCheops x ɸCheops = (3,142857 x 1,61859) = 5,0869969
1835,791 : 3602 = 0,014165… ≈ (π – 3) : 10 = 0,014159…
Ou , de manière plus simple, mais plus approchée , nous la pouvons dériver avec la formule suivante
ɸ2/π + 1 = 1,8333461…
Ce nombre – qui est un peu inexact par rapport à la constante qui détermine la relation inverse entre la masse et le rayon dans le proton et l’électron – est cependant presque parfait pour définir la relation entre la force magnétique ( Fmp et Fme) et la force gravitationnelle (Fgp et Fge) exprimées par un proton et un électron. Pour commodité , nous passons en revue les calculs que nous avons effectués précédemment
Fmp/Fgp = 4,17 x 1042
Fme/ Fge = 1,24 x 1036
4,17 x 1042 : 1,24 x 1036 = 3.362.903,2258
Prenant la racine carrée de ce nombre , nous avons vu que
√3.362.903,2258 = 1833,822…
Ce nombre correspond de manière qui semble significative a ce que nous avons vu ci-dessus (ɸ2/π + 1 = 1,8333461…).
Curieusement, ce nombre peut aussi être obtenu à partir du nombre de particules élémentaires connues par les Dogon, qui est de 266, étant donné que 266 x (2π + 1/ɸ) = 266 x 6,901219… = 1835,724.
Cependant , aussi laissant tomber cette curiosité archéologique-scientifique , nous savons maintenant que à partir des équations que nous avons vu jusqu’à présent , nous pouvons transformer les équations de la mécanique quantique «ancienne» en fonctions de ɸ et π . Et ces fonctions de ɸ et π pourraient être ce que Platon appelle «éléments» . Puisque dans son esprit – comme dans l’ Égypte ancienne – il n’y avait pas de différence entre l’abstraite théorie géométrique- mathématique et la réalité, il pourrait très bien signifier une fonction mathématique comme un «élément» de la réalité microscopique, ou comme un cycle cosmique , etc.
9. Mais nous allons discuter plus profondément ce sujet dans un article qui va à suivre, parce que – pour absurde que cela puisse paraître – dans ces proportions fondées sur π et ɸ pourrait être caché aussi le point de départ pour arriver à la théorie du champ unifié que les anciens Égyptiens avaient probablement déjà découvert à l’ époque de la construction des pyramides de la soi-disant quatrième Dynastie. Dans cette théorie le champ gravitationnel serait considéré comme une émanation de l’état du champ magnétique, c’est à dire, sa diffusion dans l’espace ; ou, vice versa, étant donné que les grandeurs sont reliées par l’intermédiaire du rayon, le champ magnétique pourrait être considéré comme un état particulier du champ de gravitation. Ce n’est pas – en général – une nouveauté, étant donné que la théorie de la relativité nous a déjà averti que l’énergie peut être considérée comme un état de la matière, et la matière comme un état de l’énergie. De cette façon, nous aurions également expliqué l’origine du monophysisme comme théorie religieuse : si ces hypothèses correspondent à la réalité , nous avons que chaque entité est elle-même et, au même temps, est toutes les autres, et toutes ensemble sont Un. Dans une conception comme celle-ci l’espace lui-même doit être considéré comme une force : de cette manière le sens de la valeur de d² dans une formule comme celle de Newton changerait complètement.
Cette valeur ne serait plus considérée comme l’effet d’une entité passive et amorphe (précisément , la distance), mais comme l’activité d’une force qui s’oppose aux effets de la masse sur une autre masse , et donc comme une sorte de force de la gravité de signe contraire .
Tout d’abord cela peut nous choquer sur le moment et nous sembler complètement incompréhensible, mais, en réalité, cela n’est rien de plus que la théorie de la relativité portée à ses conclusions logiques : si la masse peut avoir un effet sur l’espace-temps, parce que l’espace – temps ne devrait pas avoir un effet sur la masse ? (Ceci est la raison pour laquelle nous avons laissé entendre ci-dessus que, si notre thèse correspond à la réalité, des gens comme Einstein , Bohr , Heisenberg , Hawking, auront passé toute la vie à chercher le chapeau qu’ils avaient sur leurs têtes).
Mais nous allons discuter plus profondément ce sujet dans un écrit suivant, dans lequel nous allons démontrer aussi que la relation mathématique entre le mètre de la Grande Pyramide et celui actuellement en usage dans l’Occident est presque identique à celle entre G et h. De cette façon, nous allons démontrer aussi que les anciens Égyptiens possédaient ces deux unités, en plus de la coudée, la demi-coudée, etc. (la source de toutes leurs unités de mesure de longueur semble être un millimètre égal à 1,0066 de nos millimètres). Rappelons que la charge magnétique d’un électron exprime une force égale à 4,17 x 10-46 par rapport à celle de son champ gravitationnel , et que sa masse est égale à environ 1/1836 celle du proton. Si nous faisons x = 4,17/1836, et puis 1/x nous obtenons 440,28… un nombre que au niveau numérologique correspond de manière pratiquement parfaite à la longueur d’un côté de la Grande Pyramide.
Et il semble plutôt remarquable aussi le fait que nous pouvons obtenir une bonne approximation de la valeur de cette constante cosmologique même en faisant la racine cubique de la durée exprimée en années solaires d’un Jour de précession, comme 3√72,2222 = 4,16444 .
Par contre, si nous divisons 1835,791 par l’un des deux nombres typiques du cycle de Sirius et puis nous élevons le résultat au carré et multiplions par deux, nous voyons que (1835.791 : 1460)2 x 2 = 1,25653 …2 x 2 = 3,162064736… , un nombre presque identique à √10 = 3,162277 et donc très similaire, comme nous l’avons déjà vu, au produit de la constante ħ de laquelle on obtient la vitesse de la lumière, comme c x ħ = 3,161526.
10. L’enquête scientifique qui devrait comprendre la signification de la Grande Pyramide est, par conséquent, de ce genre. On peut supposer que ce sera beaucoup , beaucoup plus difficile que ce qu’on pourrait s’attendre d’une culture qui en ce qui concerne les mathématiques et l’astronomie, dans l’opinion officielle est estimée à un niveau qui n’excède pas celui de nos écoles élémentaires. Déjà les résultats de cette recherche nous poussent à poser des problèmes qui jusqu’à présent ont été complètement inimaginables.
Dans le livre de Graham Hancock « The Holy Grail Quest » (Chapitre 6, p . 128) on montre un fait en apparence insignifiant . Au milieu du XIXème siècle, un délégué du patriarche d’Arménie avait visité l’Abyssinie. Son intention était celle de démentir que toute la nation croyait fermement que l’ Arche de l’Alliance avait été transportée à Axum et qu’elle y était toujours préservée. Après un long questionnement, les prêtres axoumites montrèrent au délégué – dont le nom était Dimotheos – une table en marbre rouge, 24 cm de longueur, 22 cm de largeur et 3 cm d’épaisseur. Les prêtres lui dirent que ce serait une des deux tables de pierre contenus dans l’Arche. Le volume de ces deux tableaux s’élève à 3168 cc.
Si nous divisons ce chiffre par 10000 nous obtenons une valeur de 0,3168, qui est le cosinus d’un angle très proche de ce qu’il a pour tangente la constante qui donne la vitesse de la lumière (71°,5304, ce qui correspond à une tangente de 2,9939784, contre une valeur de c = 2,9979246, correspondent à un angle de 71°,55315 (curieusement, si nous faisons le rapport entre l’angle qui a une tangente égale à 2ɸ et celui qui a une tangente égale à c, et puis nous élevons le résultat à la troisième puissance, nous avons que (72°,827.. : 71°,553..)3 = 1,017816..3 = 1,054406, c’est-à-dire encore une fois un nombre très similaire a ħ).
Si l’on divise 3168 par 3000, nous avons 1,056, un nombre assez proche à celui de ħ. Pour obtenir des mesures parfaitement adéquates à celles qui sont à même de nous donner les constantes de nos lois physiques les plus importantes c’est suffisant imaginer qu’elles ont été prises avec un (très) peu d’approximation (a noter que le produit de la constante qui donne la vitesse de la lumière et de ħ est 2,9979246 x 1,054571 = 3,1615243 ; ce nombre – et donc aussi celui qu’on peut obtenir numérologiquement a partir du volume de l’Arche – multiplié par 2 correspond avec une très bonne approximation à la constante à partir de laquelle on peut dériver la constante gravitationnelle (la formule est de 2 x 3,1626501… x ħ = 6,670).
11. Selon l’Ancien Testament , l’Arche qui contenait les tables mesurait 2,5 codées de long et 1,5 coudées de large et de haut. Déjà comme ça ces mesures semblent être très significatives.
La longueur divisée par la largeur donne 1,6666 …, un nombre très proche du nombre d’ or (1,618033…) et que en outre représente la constante pour transformer les soixantièmes de degré en centièmes de degré.
On peut supposer alors que ces mesures ont été transcrites de manière inexacte, pour ne pas transgresser un secret hermétique, représenté par des mesures beaucoup plus importantes. Ainsi, on peut imaginer que l’Arche avait une longueur de 2,618033… coudées (ɸ²), et une largeur et une hauteur de 1,618033… coudées (ɸ).
Cependant, même de cette façon les mesures de l’Arche gardent des claires allusions à ɸ et à π. Au niveau de hypothèse, nous pouvons supposer que l’unité de mesure de l’Arche était la demi-coudée. De cette manière, sa longueur est égale à 5 fois 0,5 coudées, la largeur et la hauteur égales à 3 fois 0,5 coudées. Ainsi, nous pouvons construire cette formule, caractérisé par 3 et 5 (qui, il faut le rappeler, sont les quatrième et cinquième chiffres de la série de Fibonacci) :
(2,5 x 1,5 x 0,5) : 3 = 0,625 (1/ɸ = 0,618033988…) ;
0,625 x 5 = 3,125,
Or, il est évident que 3,125 est un nombre très proche à l’approximation de π que nous trouvons dans le sarcophage de Djedefre (3,12179… : nous verrons cet argument dans The Snefru Code part. 7 ; de toute façon, la tangente d’un angle de 3°, 125 est égale à 0,054595 … , une valeur presque identique à ħ – 1).
Les 2,5 coudées de longueur sont aussi significatives par rapport à l’angle plein (et donc aussi par rapport aux jours “purs” du calendrier solaire de l’Ancienne Égypte) car 360 : 2,5 = 144, un nombre qui correspond à 2 Jours de précession arrondis au nombre entier (72 x 2 = 144) et également au 12° nombre de la série de Fibonacci. La racine de ce nombre nous donne de nouveau 12, le nombre de mois dans l’année solaire de l’Ancienne Égypte (on peut noter que ces relations numérologiques, qui pour nous ne sont rien, dans les temps anciens ont été considérées presque comme les notes de la divine harmonie, qui à son tour était considérée la Loi cachée de l’univers).
Le cycle de Sirius, divisé par deux fois la constante qui donne la vitesse de la lumière et puis par 100 nous donne un résultat égal à 1461: ( 2,9979246 ) : 100 = 1,625… : il est donc beaucoup probable que ce qu’on appelle « Arche de l’Alliance » a été l’étoile Sirius, et, naturellement, aussi les nombres associés à son cycle , qui à son tour contiennent les nombres fondamenteaux des lois fondamentales de la physique : et ce sont ces lois qui donnent à l’homme le pouvoir sur la nature (à son tour, les histoires qui parlent de l’Arche qui se déplace de Mont Sinaï à Israël, puis de Israël en Ethiopie, ne semblent qu’une façon hermétique-allégorique de parler des observations astronomiques qui sont possibles d’abord dans un endroit, puis dans un autre).
Cette hypothèse est renforcée par le fait que plus tard dans le christianisme la Vierge Marie a été appelée « Arche de Dieu ». Et les liens entre la figure de la Vierge et celle d’Isis – la très importante divinité de l’Ancienne Egypte associée a Sirius – résultent clairement déjà dans l’Apocalypse. Parmi beaucoup d’autres choses que nous pourrions citer pour prouver ce fait historique, il semble important rappeler que dans l’Egypte a été retrouvé une figure représentant Isis couronnée de 12 étoiles, débout sur la Lune (il est facile d’imaginer que le dragon mentionné dans le Livre de l’Apocalypse peut être une transfiguration de Seth) .
De cette façon , nous aurions aussi expliquer pourquoi Flegetanis, un personnage du Parzival de Wolfram von Eschenbach, « vu les secrets cachés dans les constellations (et) a déclaré qu’il y avait une chose qui s’appelle le Graal dont il lisait clairement le nom dans les étoiles ».
12. Les liens entre la culture israélite et l’ ancienne Égypte ont été jusqu’à présent ignorés ou sous-estimés radicalement. Il est donc très utile dans ce contexte de rappeler que selon la loi hébraïque est considéré comme Israélite celui qui est né d’une mère israélite. Mais il convient de noter que la femme d’Abraham était stérile (même si elle a eu miraculeusement un enfant à l’â de 90 ans environ). Ainsi, la première Eve du peuple israélite était une servante de sa femme, qui était une Egyptienne. Donc, si nous suivons le témoignage de l’Ancien Testament, nous devons penser que le peuple Egyptien et le Juif sont étroitement liés, parce qu’ils partagent – au moins en partie – le même sang.
Il n’est donc pas surprenant que même dans les chiffres relatifs au Déluge et à l’Arche de Noé il y a probablement des allusions hermétiques à la sagesse de l’Ancienne Égypte, qui ont pu être absorbées par le peuple israélite à travers la médiation de Moïse, qui, comme nous le savons tous, selon la tradition biblique a été adopté par la fille du Pharaon et élevé comme un noble égyptien.
Par exemple, si on prend les chiffres associés aux dates et on fait la somme de ceux qui se réfèrent aux mois (= 22) et de ceux qui se réfèrent aux jours (= 81) et ensuite on fait le produit il en sort un nombre apparemment tout bien insignifiant, le 1386. Mais si on fait la relation avec le nombre typique du cycle de Sirius nous voyons que 1461 : 1386 = 1,054112554112554 , ce qui serait encore une fois une valeur très proche à ħ, qui est calculé égal à 1,054571.
Un nombre très similaire sort même dans le Timée, quand Platon indique l’intervalle harmonique minimal utilisé par le Démiurge pour générer le monde, qui est de 256 : 243 = 1,053497. On a aussi le même nombre par le rapport entre le nombre de jours d’une année solaire et ceux (346,6) d’une soi-disant « année des éclipses », étant donné que 365,25 : 346,6 = 1,053808 . Un résultat similaire peut être atteint par la (346,6 : π) racine de 346,6 , comme 346,6 : π√346,6 = 110,32…√346,6 = 1,054438. Il semble aussi remarquable que [(346,6 : 100) : e]2 = 1,625…, un nombre qui nous ramène encore une fois aux mesures de l’Arche.
Et même dans la Grande Pyramide nous trouvons quelque chose comme cela. Si l’on considère que ses mesures en coudées peuvent être obtenues à partir du nombre des jours « purs » de l’année solaire (360) en ajoutant ou en soustrayant 80, nous pouvons construire le rapport (360 : 280) : (440 : 360) = 1,051948 … (qui correspond plus ou moins à π/3) tandis que – comme nous avons déjà vu – le volume de l’Arche divisé par 3000 donne 3168 : 3000 = 1,056 : tous ces nombres, de façon très significative, semblent des approximations de ħ.
On peut obtenir un nombre très semblable à celui-ci en utilisant un des nombres typiques du cycle de Sirius, étant donné que 1460 : 10√1460 = 146√1460 = 1,05117 (Notons en passant que la hauteur de la Grande Pyramide exprimée en mètres est égale à 146,56 : en divisant par 10 le nombre typique du cycle de Sirius on constate immédiatement et presque visuellement la connexion entre 146,5 et 146, ou 146.1 ; il semble important aussi le fait que en divisant le nombre typique de Sirius par la longueur d’un côté de la Grande Pyramide, nous arrivons à ( 1461 : 440 ) : 2 = 1,6602 : le même résultat qui peut être atteint en divisant 1461 par la hauteur et puis par π : ( 1461: 280 ) : π = 1,6608 ) .
On peut obtenir un résultat même plus intéressant en divisant le cycle typique de Sirius , 1460, par la hauteur de la pyramide de Khephren, puisque 1460 : 143,5 = 10,1742 … ≈ 2ɸπ = 10,1664 . En divisant le nombre de jours d’une année des phases lunaires par ce même chiffre on a 354,36 : 143,5 = 2,4694 ≈ π/22 = 2,4674.
Si nous faisons la même opération avec la durée de l’année solaire, nous obtenons 365,25 : 143,5 = 2,5452…≈ πɸ/2 = 2,5416. En utilisant les jours « purs » de l’année solaire nous pouvons obtenir 360 : 143,5 = 2,5087 ≈ 3,16/22. On peut également noter que le cycle de Sirius – divisé par le nombre de jours d’une ” Année des Eclipses ” – donne lieu à un résultat encore une fois très intéressant, étant donné que 1461 : 346,6 = 4,2152… ≈ ɸ3 = 4,23606 (3√4,2152 = 1,61537). Au lieu de cela , divisé par une année de phases de la lune , le résultat est égal à 1460 : 354,36 = 4,1201 ≈ (ɸ2/2) x π = 4,1123.
Avec notre recherche, nous serions alors arrivés au point de comprendre le sens de ces étranges légendes qui circulent autour de l’Arche de l’Alliance. Si elle contient symboliquement, par exemple, des secrets scientifiques sur la lumière et la radioactivité, le fait que Moïse a un visage lumineux intolérable quand descend du mont Sinaï – où il a reçu l’Arche directement du Seigneur – devient une allusion mythique à la puissance de la science qui est hermétiquement contenue dans les mesures et donc dans les nombres qui définissent l’Arche. Comme nous l’avons vu ci-dessus, une plaque de fer ordinaire peut contenir codés les fondements de la science et donc de ses pouvoirs, d’une autre manière inconcevables.
Cela signifie que à faire tomber les murs de Jéricho n’aurait pas été l’Arche elle-même, mais le pouvoir que dérivait de la science contenue en elle. Mais dans l’histoire tel pouvoir est symboliquement attribué à l’Arche. Une façon de s’exprimer un peu étrange, mais compréhensible : un peu comme si nous disions que a été Einstein à détruire Hiroshima et Nagasaki, ou que c’est lui qui fait fonctionner les centrales nucléaires. Pris à la lettre, ces descriptions sont certainement trompeuses . Cependant , dans un sens moral ou symbolique ces sont certainement des vérités. Après tout, Einstein lui-même se sentait responsable de la puissance destructrice qui dérivait à partir de sa théorie.
13. En conclusion, nous pouvons dire que ce système merveilleux et presque miraculeux de congruences astronomiques, physiques et métrologique – trigonométriques que nous avons trouvé dans ces pages ne peut pas être un cas. Qu’il y ait un système décimal dans lequel 130√103 a pour résultat la constante fondamentale de la mécanique quantique, qui à son tour est codée dans l’angle correspondant à la division entre l’exposant de la racine et celui de la puissance, qui à son tour correspond à une de ceux qui sont dans l’intervalle de variation de l’inclinaison de l’axe polaire de la terre par rapport à celui de l’écliptique, ne peut pas être un cas.
Il est suffisant d’adopter une trigonométrie dans laquelle l’angle plein est divisé en un nombre de parties différent de 360, ou une métrologie différente de celle qu’en fait est en usage et le système de correspondances s’annule complètement. Il est clair que le système métrique et tout ce qui va avec, vient à travers des traditions hermétiques très anciennes. Parce qu’il est certainement dans les insondables profondeurs de temps qui a été inventé ce système numérique, dans lequel on parvient à un accord miraculeux entre les chiffres de la trigonométrie pure, celles de la physique classique et quantique et celles relatives aux cycles cosmiques regardant la Terre.
Nous ne pouvons même pas exclure que dans un passé très lointain des voyageurs en provenance des profondeurs de l’espace aient choisi de s’installer dans cette planète, car elle était la seule – ou au moins la première qui ils ont trouvé – dans laquelle les nombres de la physique et de la géométrie ont coïncidé avec ceux des cycles cosmiques . Aucune hypothèse n’est maintenant risquée, étant donné l’impossibilité que ce que nous avons vu dans ces pages puisse être attribué au hasard .
A partir de maintenant , en étudiant la géométrie de tradition pythagoricienne, nous devons nous demander : qui a été capable de développer un système abstrait qui puisse d’une façon tellement minutieuse correspondre à des quantités infimes comme celles détectées par la physique microscopique ? En effet, si la somme de tangente, sinus et cosinus d’un angle égal à π/2 correspond à ħ ; si on fait 1/x avec x égal au cosinus d’un angle dont le sinus est égal à 1/π (ce qui est l’angle de 18°,56..) et encore une fois nous trouvons ħ ; si on élève au carré la somme de sinus et cosinus de ce même angle et l’on trouve une valeur très proche de la charge élémentaire ; si quand on somme le sinus, le cosinus et la tangente de cet angle et on trouve la valeur exacte de la charge élémentaire : comment pouvons-nous oser même seulement imaginer que ce soit un système de coïncidences ? Comment des coïncidences peuvent former un système ? Le système est toujours le travail de l’intelligence !
Dans un angle égal à 20 x ɸ = 32°,36 … la somme de sinus et cosinus est 1,3799 … , qui est pratiquement égale à 1 + 1/ɸ2 = 1,381966. Dans un angle égal à 10 x π = 31,41592.. la tangente est égale à 0,61078.., qui à son tour correspond encore une fois à une très bonne approximation de 1/ɸ. Comment peut-on croire que cela est un miracle du hasard? Au contraire, il semble que nous sommes en mesure de voir – à travers ces exemples que nous avons déjà fait et par tous les autres que nous pourrions faire – que la trigonométrie se tourne mystérieusement autour de ɸ et de π , car la réalité elle-même tourne autour de ces chiffres .
Cette découverte semble démontrer sans équivoque que l’homme – si de quelque chose il descend – ce n’est certainement pas du singe, et que la sagesse qui a développé cette merveille a ses racines dans des domaines impénétrables de temps et peut-être d’espace dont peut-être nous ne pouvons pas imaginer, même vaguement, la profondeur. Ce semble maintenant hors de doute.
Peut-être que le sort ultime de notre civilisation mourante, le destin ultime qui est laissé à ceux qui ne disposent plus d’un destin, c’est de découvrir la terre où ces origines s’enracinent. Et il est bon de se dépêcher, parce que le temps qui nous reste n’est pas beaucoup.
Gabriele Venturi
Annexe 1: Le triplet pythagoricien obtenu des nombres typiques du système calendrier Maya Haab’ – Tzolkin par rapport à la plaque de métal trouvée au bout du puits stellaire sud de la Chambre du Roi et quelques notes sur les relations entre les anciens calendriers et le concept pythagoricien de l’harmonie des sphères
Les nombres typiques du système calendrier Maya Haab’ – Tzolkin sont , comme il est connu , le 18 et le 13. A partir de ces chiffres, comme avec tous les couples des nombres entiers , on peut obtenir un triplet pythagoricien qui correspond à un triangle qui a les mesures suivantes
13² + 18² = 169 + 324 = 493 hypoténuse
18² – 13² = 324 -169 = 155 côté
2 x 13 x 18 = 468 côté B
sen α = 155 : 493 = 0,314401…: Notez que cette valeur correspond presque parfaitement à
π/10 = 0,3141592…
angle α = 18°,324694 Ici il faut noter que si l’on sépare ħ = 1,054571688 en ses composantes entières et décimales et après on fait la relation, on a 1,0,054571688 = 18,32452…, avec une différence de 17/10000.
angle β = 71°,675305 la somme de sinus, cosinus et tangente de cet angle est égale à 4,28304… tandis que 2π – 2 = 4,28318…
(sinus α + cosinus α)2 = 1,26369.. 2 = 1,59691… Si de ce chiffre nous soustrayons 1 nous obtenons 0,596916… , un nombre remarquablement similaire au résultat du rapport entre la constante du moment magnétique du proton 2,793 et celle de sa masse au repos, étant donné que 1,6726231 : 2,793 = 0,598862
La tangente de β 71°,675305 = 3,01935…
La tangente de l’angle opposé au côté supérieur de la plaque de métal trouvée au bout du puits stellaire Sud de la Chambre du Roi – correspondant à un angle de 71°,55315 – était 2,9979246 . La différence entre ces deux valeurs est égale à 0,0214 .
La relation entre l’hypoténuse et le côté B est égale à 493 : 468 = 1,0534188 … ; ce même rapport , dans le cas de la plaque de métal égyptienne, était égal à 1,05416554, avec une différence de -0,00074674 . La différence avec ħ = 1,054599 est égale à -0,001180196, soit un peu plus que 11/10000 .
Un nombre similaire est également présent dans le Timée, lorsque Platon indique l’intervalle harmonique minimal utilisé par le Démiurge pour générer le monde , qui est de 256 : 243 = 1,053497 . Dans ce cas, la différence avec le nombre Maya est + 0,0000782 .
Il semble digne d’attention le fait que nous pouvons obtenir une très bonne approximation de ħ avec une simple élaboration mathématique de l’angle avec le sinus égal à 1/π. Cet angle est de 18°, 560744 , et son cosinus est 0,947986717 … .; en faisant 1/0,947986717 nous obtenons 1,0548671, différent du chiffre exact de ħ de moins de 3 milliers. Qui sait, peut-être résultera plus qu’une simple curiosité le fait qu’un angle très proche de 18°,560744 est le plus petit du triangle rectangle qui résulte du triplet pythagoricien que nous pouvons obtenir de 18 et 13 (18°,324694). Et , aussi incroyable qu’ il pourrait sembler, la somme de sinus, cosinus et tangente de 18°,560744 nous donne aussi le chiffre de la charge élémentaire , étant donné que 0,3357746… + 0,9479867… + 0,3183098… = 1,602
Un autre cycle très important pour les Mayas était celui de Vénus . Tout d’abord, nous pouvons voir que Vénus fait 13 révolutions autour du Soleil pendant le même temps que la Terre en fait 8. Cela signifie que si la terre prend 365,25 jours pour faire ce tour, Vénus en emploie seulement 225, ce qui signifie que le rapport entre ces cycles est égal à 365,25 : 225 = 1,62333 … , soit un nombre très similaire à ce qui résulte de ces deux termes successifs de la série de Fibonacci 13, 8 (13 : 8 = 1,625). Cela nous amène à la même proportion qui sort du cycle de Sirius divisé par 2 fois la constante qui donne la vitesse de la lumière, puis par 100. En effet, comme on a vu, 1461 : (2,9979246) : 100 = 1,625. Un résultat comparable sort aussi des mesures de l’Arche, qui, comme l’avons vu, sont caractérisées par un rapport de 0,625 .
En rapportant le cycle de Sirius avec celui de Vénus nous obtenons de nouveau le même nombre, puisque (1461 : 225) : 4 = 1,623333 .
Prenant comme point de référence la Terre, le cycle de Vénus apparaît d’une manière complètement différente. En fait, à un certain moment, la planète disparaît vers le crépuscule, pour réapparaître ensuite 8 jours plus tard dans la matinée, juste avant l’aube. Après 263 jours (environ neuf mois) d’errance se rapproche du soleil dans le ciel et disparaît à nouveau, restant apparemment absente pour environ 50 jours pendant qu’elle passe derrière le Soleil (notons en passant que le 50 est aussi le nombre typique du cycle de Sirius B autour de Sirius A, qui est très important pour la culture Dogon, autrefois étroitement liée à celle de l’ancienne Égypte). Puis il redevient visible pendant 9 mois. Pendant ce temps, la luminosité augmente jusqu’à ce qu’elle atteigne un maximum.
Vénus termine ce cycle en 584 jours, un nombre que les Mayas ont enregistré avec précision et qui pour eux était sacré. Nous pouvons constater que 584 ≈ (2ɸ2 + 1ɸ) x 102 = 585,41, ainsi que les deux semi-cycles de 263 jours sont très proches de ɸ2 x 102 = 261,8. Il est naturel de noter ici que les deux nombres typiques du calendrier Tzolkin sont également connexes avec ɸ2, puisque les 260 jours du total d’un cycle Tzolkin sont plus ou moins égaux à ɸ2 x 102 = 261,8 , tandis qu’une fraction de 13 jours est plus ou moins égale à 5 x ɸ2 = 13,090 .
Si nous faisons le rapport entre la durée du cycle observé du point de vue du Soleil (225 jours ) et du point de vue de la Terre, nous voyons que le résultat a encore une fois à voir avec le nombre d’or, puisque 584 : 225 = 2,59555, un nombre de nouveau très similaire à ɸ2 = 2,618033988 .
En ce qui concerne le cycle de Sirius , nous voyons que ce nombre (584) assume également des raisons d’intérêt, car – si nous prenons le deuxième nombre typique du cycle – 1460 – nous voyons que le rapport est égal à 1460 : 584 = 2, , soit en pratique la longueur de l’Arche de l’Alliance expimée en coudées . Et nous avons déjà vu que ce nombre est très important à la fois par rapport à un angle de 360 et donc aussi comparé au nombre des jours « purs » de l’ancien calendrier solaire égyptien, parce que 360 : 2,5 = 144 , un nombre qui correspond à 2 Jours de précession arrondis à l’entier (72 x 2 = 144 ) et également au 12e nombre de la série de Fibonacci. En fait, la racine de ce nombre nous donne de nouveau 12, le nombre de mois dans l’année solaire de l’ancienne Égypte. En outre, comme nous l’avons vu plusieurs fois, le 144 est un nombre qui a profondément à voir avec les constantes de la physique des particules.
Dans ce contexte , il semble particulièrement important de noter que 584 x π = 1834,69, un nombre qui est très proche de la constante qui détermine la relation inverse entre le rayon classique et la masse qui semble caractériser l’électron et le proton (dont la valeur exacte est 1,835,791 )
Pour les Mayas aussi les mouvements périodiques de Mars étaient importants. De ces mouvements ils ont enregistré avec précision les phases de mouvement «rétrograde», dans lesquelles la planète, dépassée par la Terre en son orbite autour du Soleil, semble reculer dans sa parabole le long de l’écliptique. Le nombre de jours écoulés entre les deux moitiés de deux périodes rétrogrades est de 780, un nombre qui , comme on peut le voir immédiatement, correspond exactement à la durée de 3 périodes Tzolkin de 260 jours chacune.
Ce cycle particulier de Mars , vu en rapport à celui de Sirius, nous permet de trouver une nouvelle relation avec des données importantes de la physique des particules, puisque 1 : [( 1461 : 780) : π ] = 1,677 , ce qui est plus ou moins la constante qui est utilisée pour calculer la masse du proton (qui est en fait 1,672). En utilisant “c” au lieu de π , nous trouvons un nombre caractéristique qui sort de les mesures de l’Arche, puisque (1461: 780) : 2,9979246 = 0,624791 , ce qui est plus ou moins le rapport de 0,625.
Par contre, multiplié par quatre et divisé par 103, ce cycle de Mars nous ramène au nombre typique du sarcophage de Djedefre , le 234 , qui, rapporté au cycle de Sirius , nous a donné une approximation de π qui était très intéressante au cours de notre recherche, en particulier pour ce qui concerne la constante de gravitation G. En effet (1461 : 234) : 2 = 3,1217… lorsque (780 x 4) : 103 = 3,12 , ce qui correspond à la tangente d’un angle égal à 72,2286 , qui numérologiquement nous renvoi au Jour de précession et , encore une fois , à toutes ses connexions avec les constantes de la physique.
Si on divise 780 par 234, nous avons encore un nombre caractéristique, le 3,333… , qui, multiplié par 2, nous renvoi au biblique « Nombre de la Bête » ou « Chiffre de la Bête[ » – 666 – qui ]est contenu dans l’Apocalypse de Jean, au chapitre 13, verset 18 (nous recordons que 13 et 18 sont les nombres typiques du système calendrier des Maya, et que 18/13 = 1,38461.., est un chiffre très proche de 1 + 1/ɸ2 = 1,381966), et aussi l’angle de 54 degrés (360 : 54 = 6,6666 …) qui numérologiquement correspond à 3/4 d’un Jour de précession. Remarquable semble aussi sa congruence avec le sinus de 138°, 19 qui est égal à 0,6666625 (138°,19 est l’angle de l’icosaèdre, l’angle le plus caractéristique entre les angles des solides de Platon, et qui peut être dérivé à partir du nombre d’or avec cette formule [1 + (1/ɸ2)] x 102).
Il semble également intéressant de noter que si nous faisons la racine « de la Bête » de la vitesse de la lumière exprimée en dix- millièmes de millimètre , c’est-à-dire, si nous faisons la racine 666 de 2.9979246 x 1015, nous obtenons une très bonne approximation de ħ, comme 666√2997924600000000 = 1,054966 .
Peut-être il est également utile de rappeler que la valeur du cycle de Sirius divisé par la constante “c” élevée au carré est plus ou moins égale à ( 13 : 8 ) x 102 = 162,5, étant donné que 1461: 2,99792462 = 1461: 8,98755190728516 = 162,558.
Par contre, si l’on divise le 780 par une « Année des Eclipses » nous pouvons obtenir 780 : 346,6 = 2,25043 …. Si l’on divise les jours «purs» du calendrier solaire Haab par ce nombre arrondi à 2,25 et élevé à la cinquième puissance nous trouvons encore une fois l’approximation de π que nous avons trouvé mettant en relation le nombre caractéristique du sarcophage de Djedefre avec le cycle de Sirius, étant donné que 360 : 2,255 = 6,2429 … et 6,2429 : 2 = 3,1214 … (il est parfois intéressant de noter que 1 : (6,2429..) = 0,16018.., cet-à-dire la charge élémentaire (1,602) divisée par 10).
Les cinq premiers livres de l’Ancien Testament ont été écrits dans un code avec lequel les 5 lettres du mot «Torah» sont scandées dans un ordre fondé sur 50. Par exemple, si à un moment donné il y a un “t” , en comptant 50 lettres se trouve un “o” et après encore 50 lettres “r” etc. Et bien sûr, le 50 résulte un chiffre numérologiquement connexe avec d’autres chiffres importants . En divisant le nombre de jours «purs» de l’ancien calendrier solaire égyptien par 50 nous avons que 360 : 50 = 7,2 , une claire allusion numérologique à 72. À son tour, 72 : 50 = 1,4444 … , ce qui est bien sûr une allusion à 144.
En outre, nous pouvons trouver le nombre typique du sarcophage de Djedefre également par moyen de 50 et 40. Si nous mettons x = 50 : 40 = 1,25 , alors x : 1/x = 1,25 : (1 : 1,25) = 1,5625 . A ce point on peut facilement obtenir une bonne approximation de πDjedefre avec 1,5625 x 2 = 3,125 .
En ce qui concerne le Nouveau Testament nous pouvons rappeler que nous ne devons pas pardonner jusqu’à 7 fois , mais jusqu’à 70 fois 7, c’est-à-dire 490 fois. Si l’on divise ce nombre par le nombre de jours « purs » du calendrier Maya et de celui de l’ancienne Égypte nous avons que 490 : 360 = 1,36111 … , un résultat très proche e/2 = 2,71828 … : 2 = 1,359 …
Si nous divisons le cycle de Sirius par ce même nombre, puis par π et enfin nous faisons 1/x nous avons que 1 : [(1460 : 490) : π ] = 1,054370 , c’est-à-dire une approximation de ħ très similaire à ce que nous avons rencontré dans la plaque de fer trouvée dans la Grande Pyramide .
Très intéressant , au niveau numérologique , est aussi la durée en années solaires du cycle de rétrogradation des nœuds de la lune, qui correspond à 18,61 années solaires . Si on le divise par 3 nous avons que 18,61 : 3 = 6,20333 … ≈ 1 / ɸ x 10 = 6,18033 . Par contre, ce nombre élevé au carré nous donne la durée de l’année de l’éclipse, qui correspond à 346,6 jours . En fait , 18,612 = 346,33 ≈ 346,6 . Il semble aussi remarquable que on puisse obtenir le nombre de jours dans l’année des éclipses à l’aide de la formule (π x √5)3 = 7,0248 … 3 = 346,66.
Les 18,61 années correspondent à 6793 jours . Divisé par ɸ8 ce nombre nous donne une bonne approximation de la durée de deux Jours de précession (144,444 années …) puisque 6793 : ɸ8 = 6793 : 46,9787 … = 144,59 . Par contre, divisé par ɸ16 ce même nombre nous donne 6793 : ɸ16 = 6793 : 2206,999… = 3,077, c’est-à-dire un nombre très proche de la constante qui nous nécessitons pour calculer le diamètre classique du proton qui, comme nous l’avons vu, est égal à 3,07. Une autre façon « cosmologique » pour obtenir le diamètre classique du proton est de diviser le nombre des jours «purs» du calendrier solaire égyptien par l’un des nombres-mesure de la précession – c’est-à-dire 13 x 9 = 117 – car 360 : 117 = 3,0769
Les Mayas avaient aussi un calendrier qui a été utilisé pour calculer des quantités de temps très grandes, qui a été appelé « Compte Long ». L’unité de temps plus longue était la « kinchiltun », qui comprend 1,152 milliards de jours . Cette unité de temps semble avoir quelque chose à voir avec ce nombre mystérieux , 888 , qui sort de la relation entre les principales mesures de la Grande Pyramide exprimées en coudées et en mètres. En fait, ce nombre , divisé par 360 au carré nous donne un résultat numérologiquement très intéressant, comme 1152000000 : 3602 = 8888,8888….
Ce même chiffre, divisé par le nombre de jours d’ un cycle de Sirius multiplié par le nombre de jours dans une année solaire, nous donne une très bonne approximation numérologique de la durée d’un Mois de précession calculé à 26 000 : 12 = 2166,6 … années solaires . En effet , 1152000000 : ( 1460 x 365,25 ) = 1152000000 : 533265 = 2160,27.
Au niveau numérologique il est intéressant de noter que Jupiter accompli un révolution autour du Soleil tous les 4332,667 jours terrestres. Si nous divisons ce chiffre par le nombre de jours « purs » du calendrier solaire Maya ou de celui de l’ancienne Égypte nous voyons que 4332,667 : 360 = 12,035. Un an « pur » sur la Terre correspond donc presque exactement à un mois de Jupiter, qui est 1/12 du temps qu’il lui faut pour compléter une révolution autour du soleil.
La période de rotation de Jupiter autour de lui-même est d’environ 9 minutes et 50 secondes, pour un total de 590 secondes. En ce qui concerne la durée de sa révolution autour du soleil, alors que dans une année solaire il y a 31557600 secondes, ce temps correspond à
(590 : 31557600) : 11,86 = 1,86959.. x 10-5 : 11,86 = 0,15763888.. x 10-5 ≈ π/20 x 10-5 = 0,157079 x 10-5
Ainsi la proportion des révolutions que Jupiter fait sur lui-même par rapport à l’année solaire est
(590 : 31557600) = 1,86959.. x 10-5
La valeur constante de ce ratio, 1,86959.., nous la pouvons obtenir avec une bonne approximation aussi de 4√11,86 = 1,85575.., avec une différence de 14/1000. À son tour, de cette valeur constante on peut facilement obtenir le rapprochement de ɸ qui se trouve dans la Grande Pyramide, étant donné que
Quant à Saturne , la durée d’une révolution autour du Soleil est égale à 29,458 années terrestres : il y a donc une correspondance numérologique presque parfaite entre ce nombre et la longueur d’un mois lunaire synodique égal à 29,5306 jours. Et , en effet , en divisant le nombre de jours de la période de révolution de Saturne par celui du mois lunaire nous avons que (29,458 x 365,25) : 29,5306 = 364,35, un chiffre très proche au nombre de jours d’une année solaire. Il est possible que ce type de rapports ait poussé les prêtres-astronomes de l’antiquité à associer l’action astrologique de Saturne avec celle de la lune.
Les distances extrêmes atteintes par la Lune pendant son orbite sont , respectivement , de 55,4 fois le rayon moyen de la Terre au périgée et 66,1 à l’apogée. Le 66 nous renvoi au biblique « Nombre de la Bête », mais en termes de numérologie c’est la distance moyenne qui est intéressante, elle correspond à 60,75 fois le rayon de la Terre. Si nous transformons numérologiquement cette donnée en un angle de 60°,75 et nous faisons la somme de tangente, sinus et cosinus, on obtient un nombre très proche de π , soit 3,14674 .
Mercure est la planète la plus interne du système solaire, avec un sommet de distance du Soleil de 57,91 millions de kilomètres et une distance minimale de 45,9 . Elle est également la plus petite des planètes intérieures. La distance moyenne du soleil est 51.9 million kilomètres. En transformant numérologiquement cette dernière donnée, nous nous rendons compte que ce chiffre est presque égal à l’angle de la base de la Grande Pyramide (51°,817), dont le cosinus est égal à 0,61817, qui est très proche de 1/ɸ .
CONCLUSION
Il semble donc que le concept de Pythagore de « harmonie des sphères », loin de dériver des superstitions mathématiques et d’un manque de connaissance du système solaire, implique au contraire une connaissance mathématique et astronomique très profonde, et la recherche approfondie de la relation entre les cycles des planètes du système solaire avec les nombres typiques des calendriers anciens et ceux des cycles terrestres (année solaire , année des éclipses, mois, phases de la lune, etc.), non moins qu’avec les nombres sacrés désormais familiers π et ɸ. Kepler donc avait complètement raison quand il a essayé de comprendre les relations entre les orbites des planètes du système solaire en termes de géométrie sacrée. Le problème est qu’il n’a pas réalisé que cette géométrie est beaucoup plus compliquée de ce qu’il imaginait.
Nous sommes conscients que ce que nous avons présenté ci-dessus n’est rien de plus qu’une esquisse, mais il peut être un point de départ pour une compréhension plus profonde de la science et de l’astronomie des anciens, et de l’ idée qu’ils avaient de l’univers comme une harmonie de sphères.
annexe 3 : TROIS POÈMES POUR S.
INTERLUDE
Ah ! cette vie de mon enfance, la grande route par tous les temps, sobre
surnaturellement, plus désintéressé que le meilleur des mendiants, fier de
n’avoir ni pays, ni amis, quelle sottise c’était. – Et je m’en aperçois seulement !
A. Rimbaud
Varsovie
Varsovie couverte de neige
et d’invisibles fleurs
qui des blancheurs illimitées
de la neige se nourrissent
et resplendissent
émerveillées.
Varsovie du ghetto,
du carnage.
Varsovie mille fois balayée
et mille fois
comme moi
ressuscitée.
Varsovie ta patrie
ton ciel.
Varsovie dans tes yeux
dans mon amour
comme un voile.
Varsovie de ton rire d’argent
et de ces intimes souffrances
dont je ne souffre plus
qui presque sont oubli.
Varsovie des pas qui retentissent
dans le silence de spectres d’une rue latérale,
d’une vie quelconque qui passe
fatiguée de tristesse
et dont après personne
ne saura rien.
Varsovie encore en vie
pourtant
sous en déluge de temps
qui jamais ne se retient.
Varsovie
qui s’éloigne
comme une vallée dans une évanescence
de brume sans destin,
vague labyrinthe
où le cœur
s’égare,
cherchant sens cesse ce qui reste
d’une perdue et splendide
douleur.
Varsovie,
je le sais,
désormais presque seul en nom
qui dans le ténu s’évanouir de la mémoire
s’évanouit et s’attenue
comme ton visage
dans une pénombre d’une tonnelle en été,
fixant un coin obscur,
là où je voudrais
rencontrer tes yeux.
PARIS (AVANT TOI, APRÈS TOI)
1. APRÈS TOI
Si je désire une eau d’Europe, c’est la flache
Noire et froide où vers le crépuscule embaumé
Un enfant accroupi plein de tristesse, lâche
Un bateau frêle comme un papillon de mai.
A. Rimbaud
Rues larges comme places,
places illimitées comme le désert
et pourtant pleines de gens qui vont et viennent. Paroles
saisies à la volée ici et là
entre le bruit du monde et de “tout le monde”
dans une langue qui résonne obsédante et possédée
par un seul nom : Arthur Rimbaud.
Puis :
musées qui érigent un mystique, fantastique, protéiforme labyrinthe,
cathédrales ivres des symboles qui défient l’abîme,
lointains horizons normands, d’acier, de tours et de cavalcades,
les barricades, les flammes, les chansons, les cris sans fin
de la Révolution, Napoléon, la Seine qui coule
lente et rapide telle que le temps et après …
Et après ?
Et après
un fleuve, une mer, un naufrage, un tourbillon des choses
qui dans la mémoire confuse et illimitée s’échappent
tels que les feux jetés par un train en marche :
les nations, les explorations, les colonies, les empires,
les peuples, le populisme, l’individu, l’individualisme,
la technique, la science, le progrès, la république,
les démocraties, la Première Guerre Mondiale,
l’après-guerre, le communisme, le fascisme,
l’existence, l’existentialisme, la crise de ’29, le nazisme,
une autre Guerre Mondiale, encore,
un autre après-guerre, encore,
la reconstruction, la guerre froide,
le développement, le Mai du ‘68,
les jeunes du Mai,
le flux et le reflux
et après …
Et après …
….et après
pourquoi lutter
pur se souvenir d’autres choses
encore?
Ici
on peut trouver tout
– et partout ! –
de sorte que rien n’est jamais
vraiment
à rechercher.
* *
Loin
la Tour Eiffel s’estompe
comme derrière une fenêtre
où le souffle silencieux étend un voile :
ce sont les larmes à la pensée
que pendant des années et des années
juste tes yeux
ont vu ce ciel.
II.
PARIS AVANT
Moi qui trouais le ciel rougeoyant comme un mur
Qui porte confiture exquise aux bons poètes,
Des lichens de soleil et des morves d’azur ;
Qui courais, taché de lunules électriques,
Planche folle, escorté des hippocampes noirs,
Quand les juillets faisaient crouler à coups de triques
Les cieux ultramarins aux ardents entonnoirs ;
Moi qui tremblais, sentant geindre à cinquante lieues
Le rut des Béhémots et les Maelstroms épais,
Fileur éternel des immobilités bleues,
Je regrette l’Europe aux anciens parapets !
A. Rimbaud
Le ciel….
Le ciel comme aveugle,
comme en aigle…
Ce ciel
loin,
parti
et ainsi…
….perdu,
comme rendu
au désert obscurci,
endurci,
sans vie
de l’hiver.
Un sourire affaibli,
apeuré
franchit l’air morne.
Rigide,
engourdi
dans la caresse gelée du vent,
le front baissé
sous ce ciel bas,
sous la pluie lente,
trop lente,
trop fine
pour l’appeler pluie
et trop épaisse
pour croire vrai ce prodige nu
– se sentir perdu dans le brouillard –
en qui pourtant
follement
il croit.
Labiles éclats
de sable noir : voici
la dure Seine
où comme goélands à l’horizon
se perdent
les voix et les frémissements
des blancs bateau
débordant de gens
qui lui semblent heureux.
Il marche
lentement,
caressant doucement
les parapets.
Plongé dans le secret
de son interne silence,
immense,
il n’entend pas les bruits :
partout
il y a de gens
et il ne voit personne.
Distrait par des souvenirs
qu’il ne sait pas d’avoir
l’adolescent timide bégaie des phrases incertaines
en cette langue nasale
que l’enfant commença peut-être à apprendre
et que l’adulte finira pour oublier
presque entièrement.
Les marbres impassibles,
Notre-Dame
impossible.
Un visage qu’il sait de ne pas connaître
– et qui pourtant il pense de reconnaître –
s’évanouit derrière le coin,
tandis que comme en proie à la fièvre il parcourt
les vastes labyrinthes du Louvre,
où à la fin chaque couloir bifurque
en ères perdues,
symboles incompréhensibles,
dieux et fois surréels,
gouffres d’événements et temps qui fondent
puis
parmi les labyrinthes du trafic,
dans le gouffre des rues
et des places gigantesques
dont presque il ne peut pas imaginer
l’énorme traversée,
les yeux éclipsés sur la vitrine obscurcie où
son vain reflet scrute celui
encore plus vain,
encore plus inhumain
de la Tour Eiffel
qui grimpe vers ce ciel
désormais tellement
loin
et tellement….
….perdu…
…éthéré,
comme dispersé
dans le désert de pierre,
de verre
de l’hiver.
Une saison à l’enfer terminait,
une autre commençait
interminablement.
Je fumais des Gauloises,
je buvais du cognac,
je pensais de chercher un autre Ailleurs
– désespérément –
mais comme un héros
fatigué et d’un autre âge
j’étais en train de revenir à la maison
et je ne le savais pas.
TES VALISES
Un coup de ton doigt sur le tambour décharge tous les sons et commence
la nouvelle harmonie.
Un pas de toi, c’est la levée des nouveaux hommes et leur en-marche.
Ta tête se détourne: le nouvel amour! Ta tête se retourne: le nouvel
amour!
« Change nos lots, crible les fléaux, à commencer par le temps », te
chantent ces enfants. « Élève n’importe où la substance de nos fortunes et
de nos vœux”, on t’en prie ».
Arrivée de toujours, tu t’en iras partout.
A. Rimbaud
Ta légèreté, tes valises, tes départs, comme je les envie !
Et je sais d’être fou. Parce que l’envie c’est la folie même.
Peut-être que l’air, l’eau et le pain
sont tout ce qu’il y à envier dans ce monde
et le reste – tout le reste – sont des fables au vent.
Je le sais trop bien tout cela, et je le répète. Et pourtant
je t’envie quand même.
Ta légèreté, tes valises, tes départs, comme je les admire !
Je les vois aller sur la surface inutile du temps
comme un magique poisson volant
qui vaguement rebondit sur les vagues
par toi béni tantôt ici, tantôt là-bas, après
qui sait où….
Je ne peux même croire
ou imaginer
que celles-ci ne soient rien d’autre
que tes chaines,
ton fardeau,
ton tourment,
ton destiné exile de toi-même
comme il est pour moi-même
de rester ici
où je ne suis pas.