LA CIENCIA ANTES DE LA CIENCIA: SUS HUELLAS Y SUS POSIBLES FUNDAMENTOS TEOLÓGICO-ASTRONÓMICOS A PARTIR DEL DESCUBRIMIENTO DE UN CÓDIGO ÁUREO DEL ESPACIO-TIEMPO EN LA GRAN PIRÁMIDE Y LAS ESTELAS DEL ANTIGUO EGIPTE

En la cuarta parte de “Une saison en enfer”: L’IMPOSSIBLE

Dans un grenier, où je fus enfermé à douze ans, j’ai connu le monde,
j’ai illustré la comédie humaine. Dans un cellier j’ai appris l’histoire. A
quelque fête de nuit, dans une cité du Nord, j’ai rencontré toutes les
femmes des anciens peintres. Dans un vieux passage à Paris on m’a
enseigné les sciences classiques. Dans une magnifique demeure
cernée par l’Orient entier, j’ai accompli mon immense œuvre et passé
mon illustre retraite. J’ai brassé mon sang. Mon devoir m’est remis. Il
ne faut même plus songer à cela. Je suis réellement d’outre-tombe, et
pas de commissions.
A. Rimbaud

PRIMERA PARTE : UNA BREVE RECAPITULACIÓN Y UN PRIMERO DESARROLLO DEL TRABAJO QUE SE HA HECHO

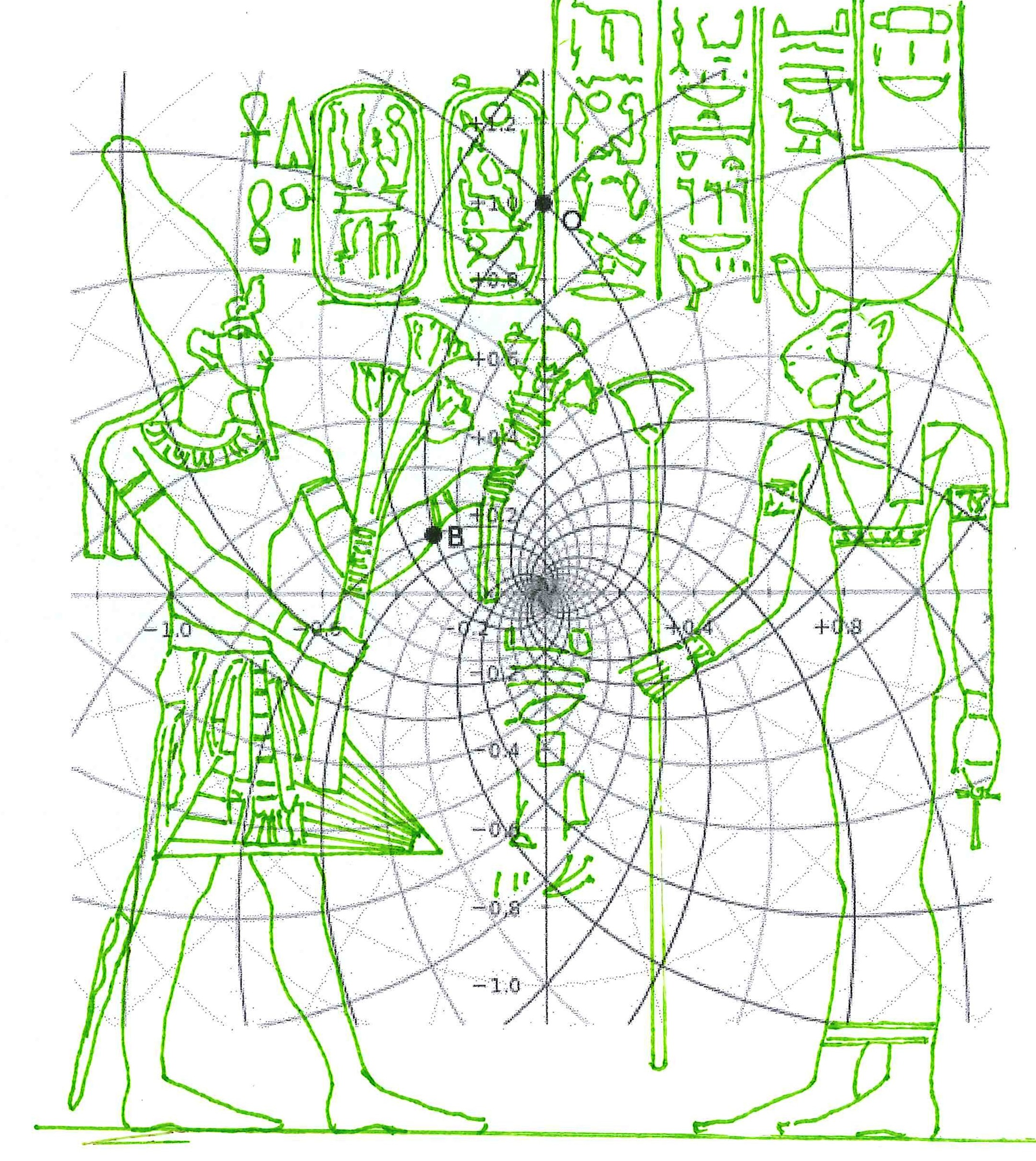
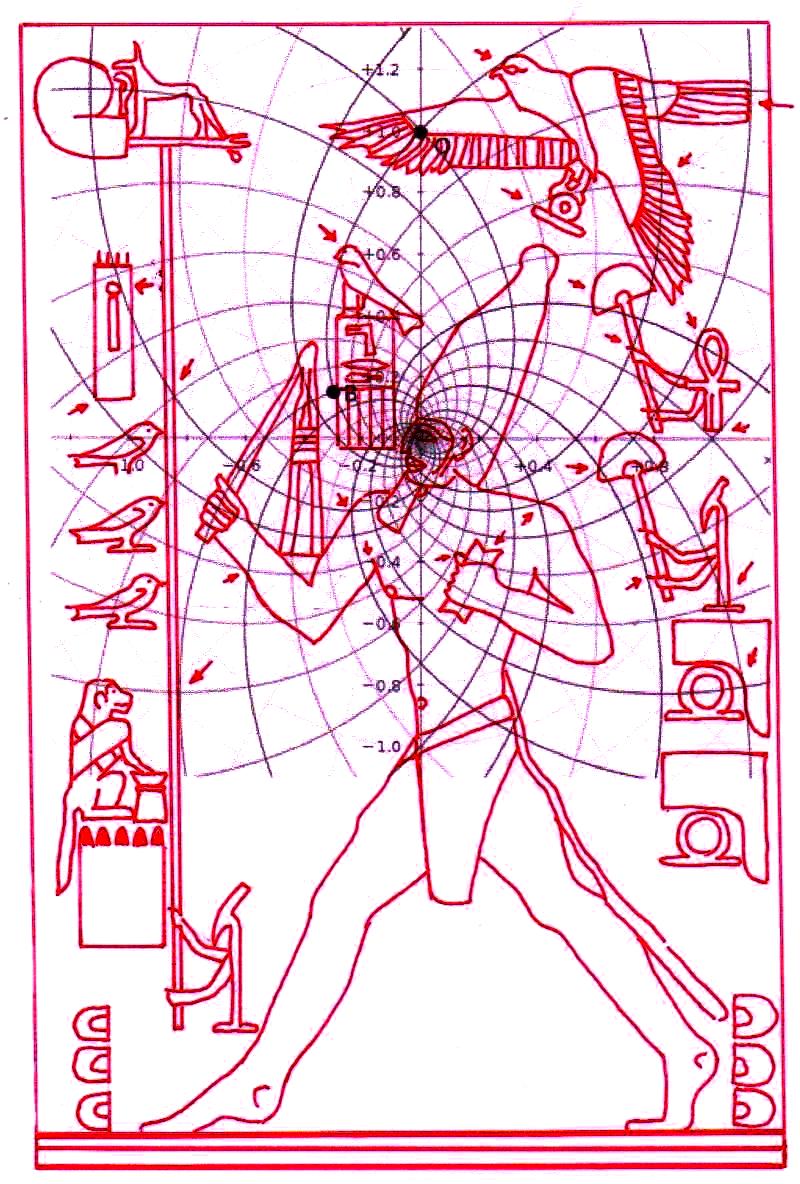
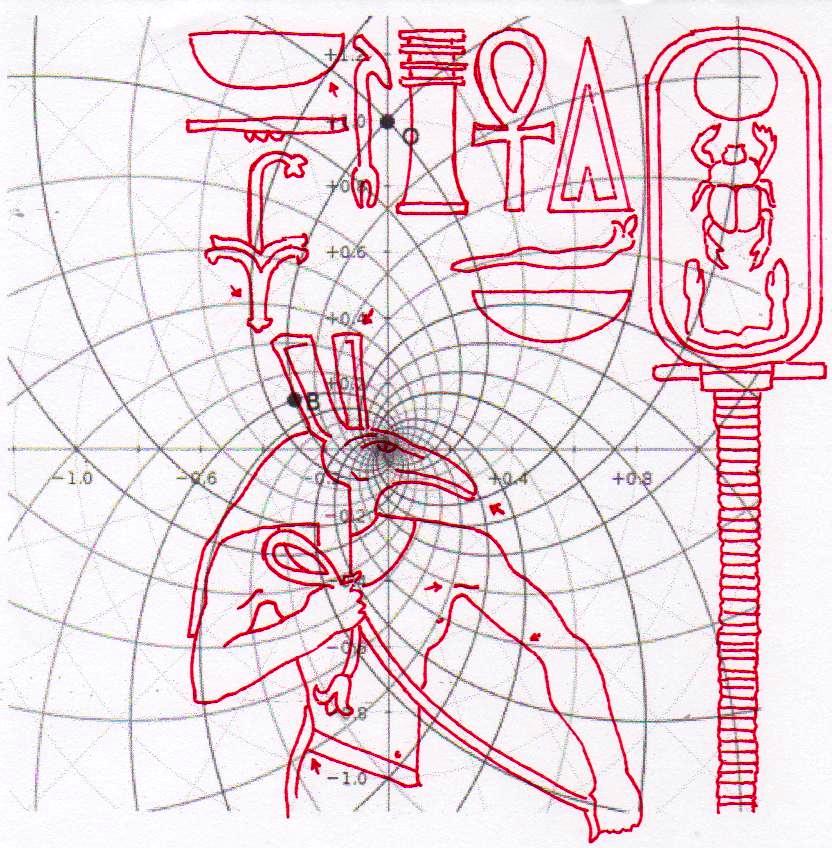
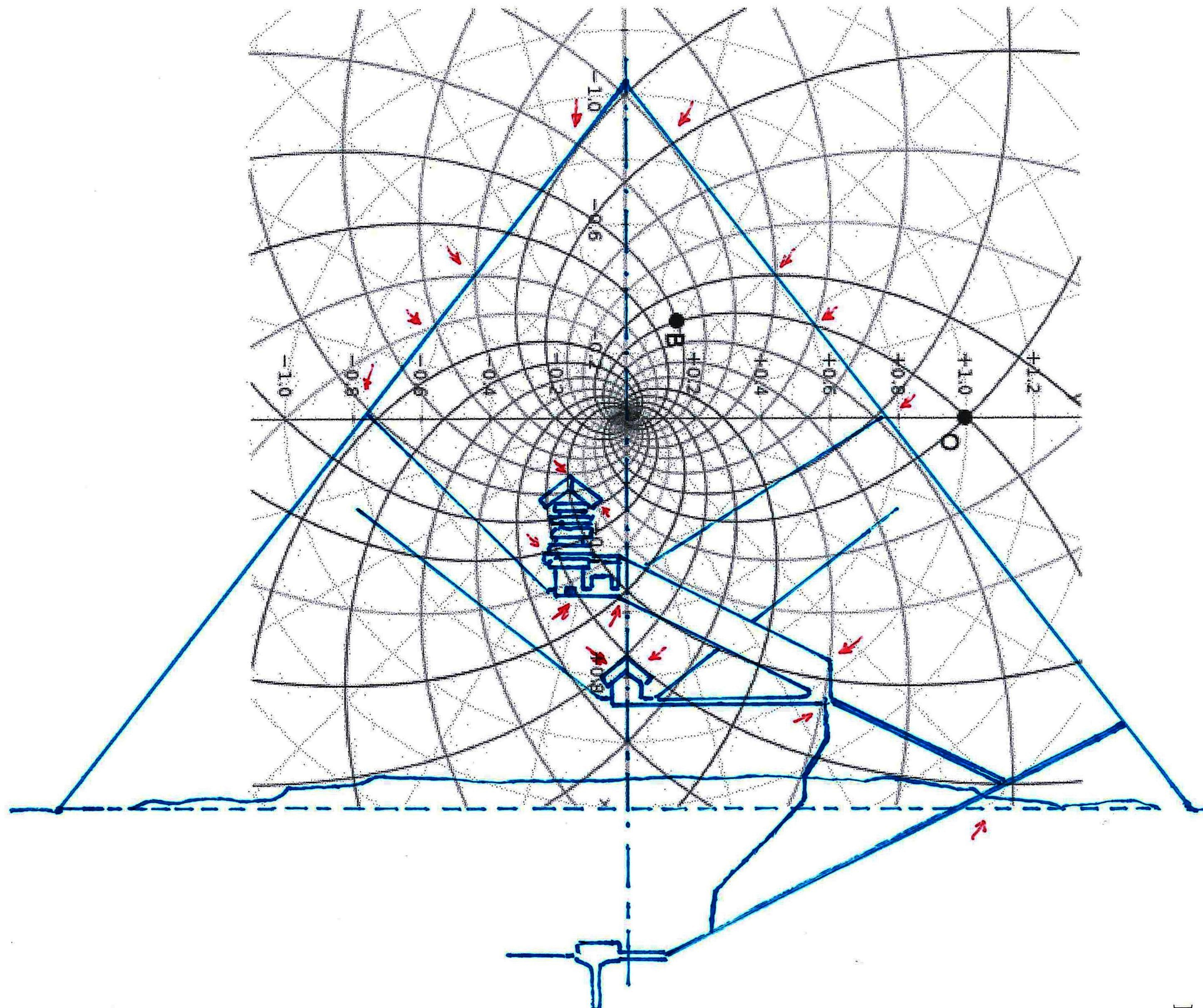
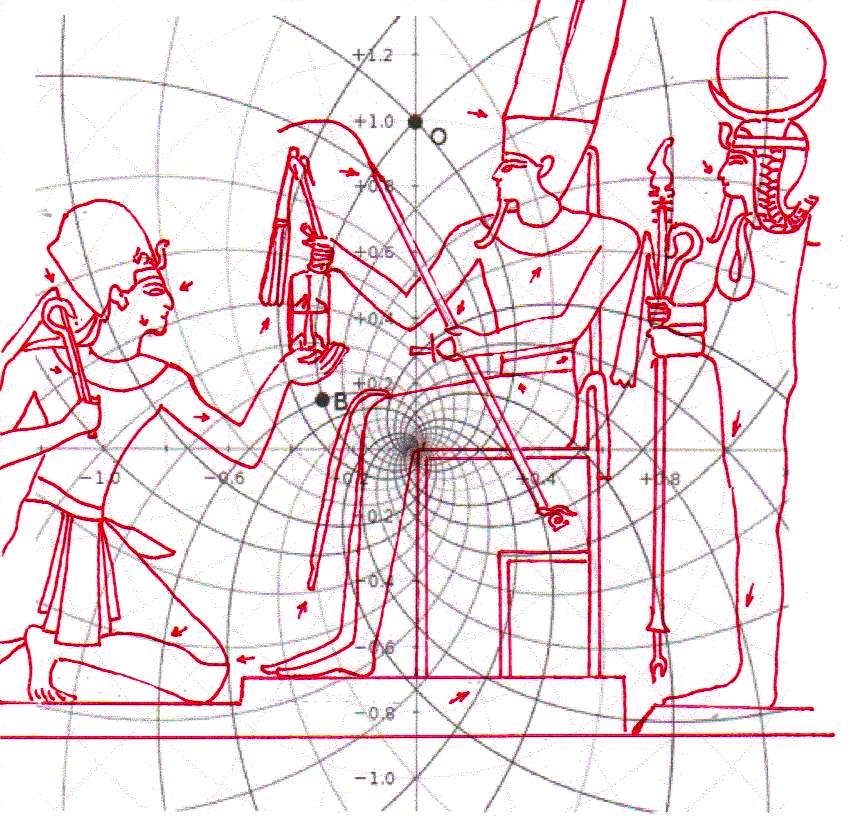
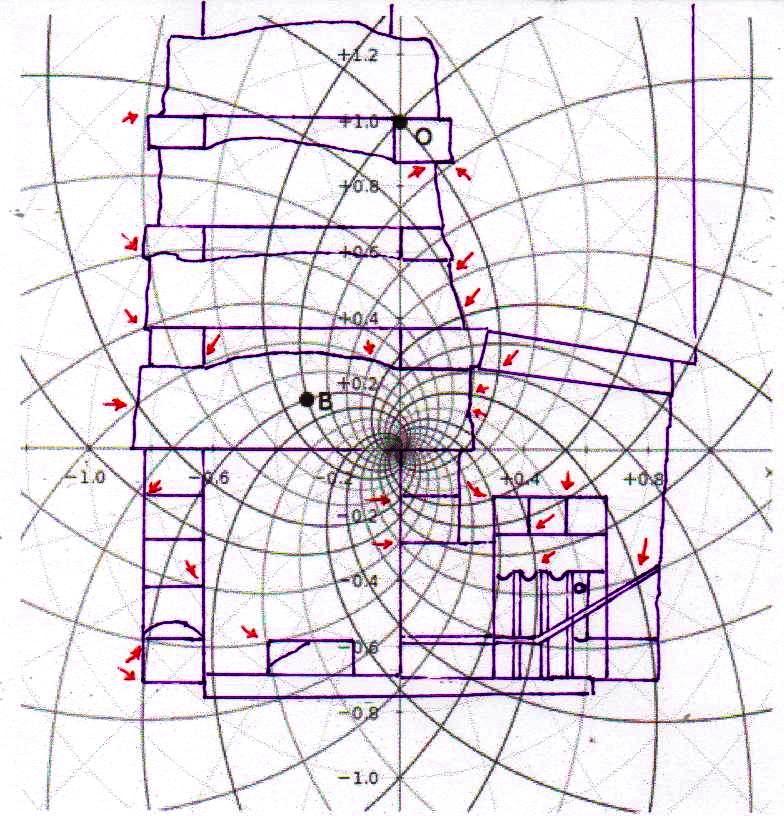
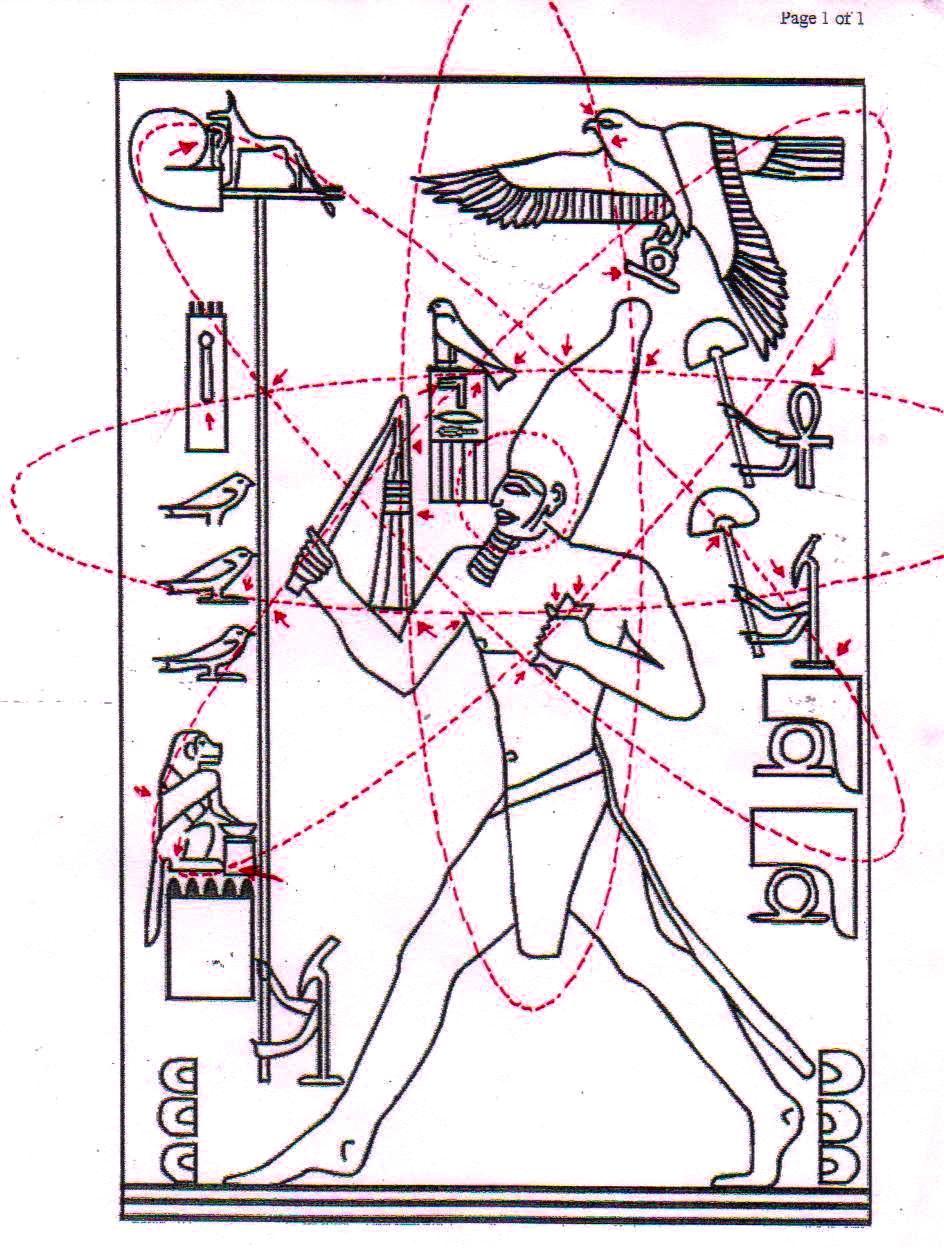
1) Antes de entrar en lo substancial de nuestros argumentos es útil y tal vez incluso necesario anteponer un breve resumen de los resultados que hemos logrado en el curso de esta investigación sobre el significado profundo del arte y la arquitectura sagrados del Antiguo Egipto, la investigación que hemos llamado “The Snefru Code” no porque el código objeto de nuestra investigación atañe sólo el famoso faraón Snefru, sino porque, de manera totalmente casual, la primera estela objeto del análisis ha sido la estela que le se atribuye, que fue hallada en una cantera en el Sinaí y que ahora se encuentra en el Museo Egipcio del Cairo. Durante la investigación sobre la geometría de las Pirámides en relación con la de los jeroglíficos y las estelas, nos encontramos frente al que podemos definir un extraño tipo de hallazgo arqueológico, cuyos contenidos han aparecido desde un principio realmente extraordinarios. En las tres primeras partes de este trabajo (correspondientes en el sitio a The Snefru Code part. 1, 2, 3), sobre la base de evidencias geométrico-visuales, que en el conjunto parecen muy difícilmente cuestionables, en un primer momento habíamos planteado el problema y después descubierto la real existencia de un código geométrico – derivado a partir de una versión de “Gold Standard” del espacio-tiempo – que parece constituir el fundamento de las proporciones y el diseño de todo el arte y la arquitectura sagrados del Antiguo Egipto. Para demonstrar esta tesis presentamos muchas imágenes de diferente tipo, que el lector puede encontrar fácilmente dando un vistazo a los artículos anteriores o, para así decirlo, hojeando un poco las dos gallery. En estas imágenes se mostró un gran número de fenómenos geométricos, extraordinariamente complejos y a veces incluso muy valiosos estéticamente, que se pueden obtener del diseño figurativo y arquitectónico del Antiguo Egipto. Todo lo que se ha hecho ha sido sobreponer las diferentes formas con referencia a puntos que por varias razones se podían imaginar geométricamente y/o simbólicamente significativos. Uno de estos puntos, por ejemplo, ha sido el ojo del Faraón, porque todos sabemos que el Faraón se creía que era el avatar humano de Horus y uno de los símbolos más importantes de esta divinidad era justo el ojo, entendido, al parecer, como una transfiguración del disco solar. En la primera de las imágenes – seguida por otras que el lector puede analizar sin más comentarios – podemos ver uno de los juegos geométricos más complejos que hemos sacado del arte sagrado del Antiguo Egipto: la Gran Pirámide con su cúspide apoyada en el ojo de Snefru, a su vez apoyado en el punto de intersección entre el ala y la parte posterior del Halcón de la estela conocida con el nombre de Djoser Running. De esta manera el perfil de la Pirámide cruza también el ojo del personaje que Snefru se prepara para golpear mientras la proyección del pozo sur de la Cámara del Rey cruza justo el ojo de Zoser. En cambio, la proyección del lado norte del perfil de la Pirámide va a tocar el centro de lo que parece ser una especie de visor, de los que en aquel tiempo se utilizaban para observar las estrellas y que más de una vez han sido representados en el ámbito del arte sagrado del Antiguo Egipto. Esto parece indicar de manera inequívoca que las partes de estas estelas que tienen que ver con el ojo humano entretienen entre sí una relación geométrica particular, causada por un código que hace posible todo este extraordinario sistema de superposiciones. Esta es una hipótesis poco en armonía con lo que solemos pensar sobre la antigua cultura egipcia, pero que surge espontánea mirando la imagen de abajo, junto con otra, de tipo astronómico. A saber, que el punto de intersección entre el ala y la parte posterior del Halcón en la estela de Zoser es la estrella de una constelación (Orión, probablemente) que tenemos que mirar con el visor en el que se apoyan, como en una especie de barca, un perro y una cobra, que a su vez podrían interpretarse como entidades celestes. Sirius, uno de los avatares astronómicos de Isis, en la antigüedad a menudo ha sido nombrado “Estrella Perro”; y esto podría significar, por ejemplo, que el perro que vemos en el visor es justo esta divinidad. Otro avatar astronómico de Isis era la Luna y en The Snefru Code part.4, se realizó un análisis que nos llevó a considerar justamente la cobra como un símbolo de la luna. Así que este complejo simbólico podría aludir a ciertas observaciones astronómicas que se pueden hacer si se tiene Sirius (y tal vez incluso la luna) como punto de referencia; observaciones que a lo mejor se relacionan con los cambios del cielo durante el ciclo de precesión, teniendo en cuenta que las tres aves a la izquierda del relieve ciertamente parecen ser una alusión a las tres estrellas polares. Thuban, la estrella polar en el tiempo cuando se piensa que este relieve fue tallado, es la estrella que se encuentra entre Vega y Polaris, y observando el relieve se puede notar que el ave que con el pico toca el asta sobre la cual es fijado el visor (asta que podría interpretarse como el eje polar) es justo el ave que está en el medio de los dos otros.

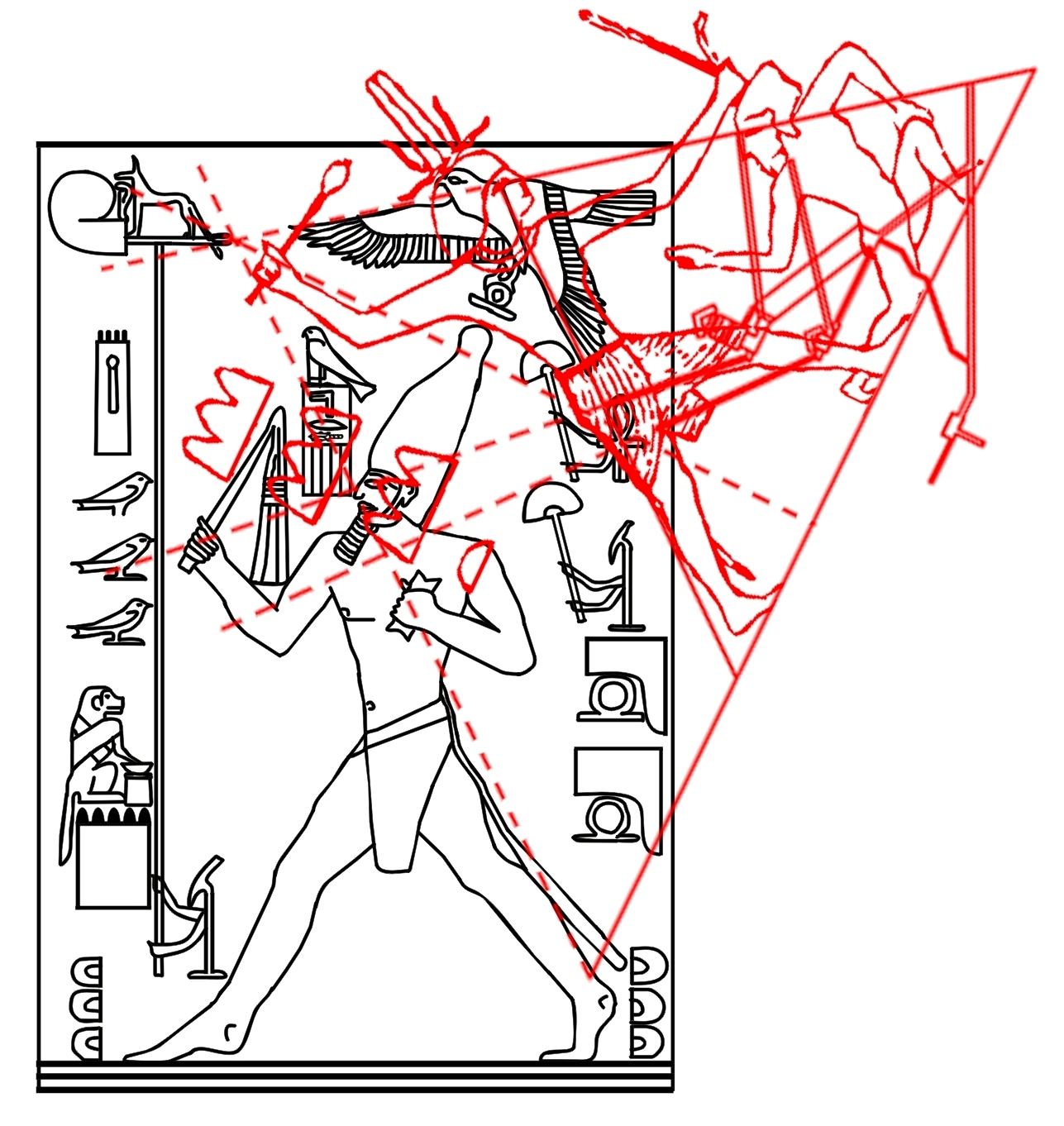
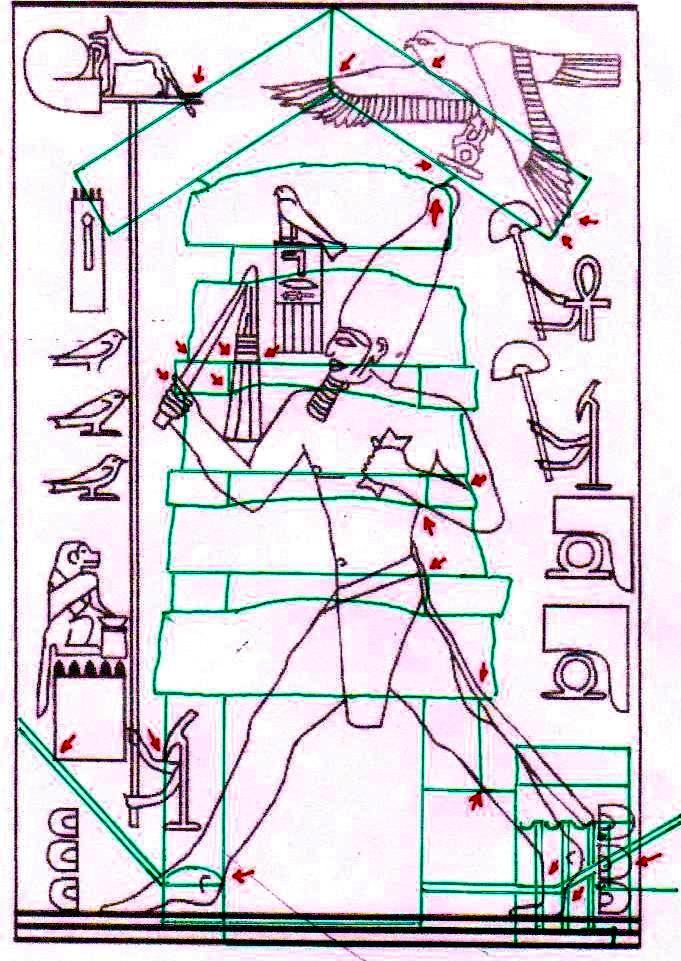
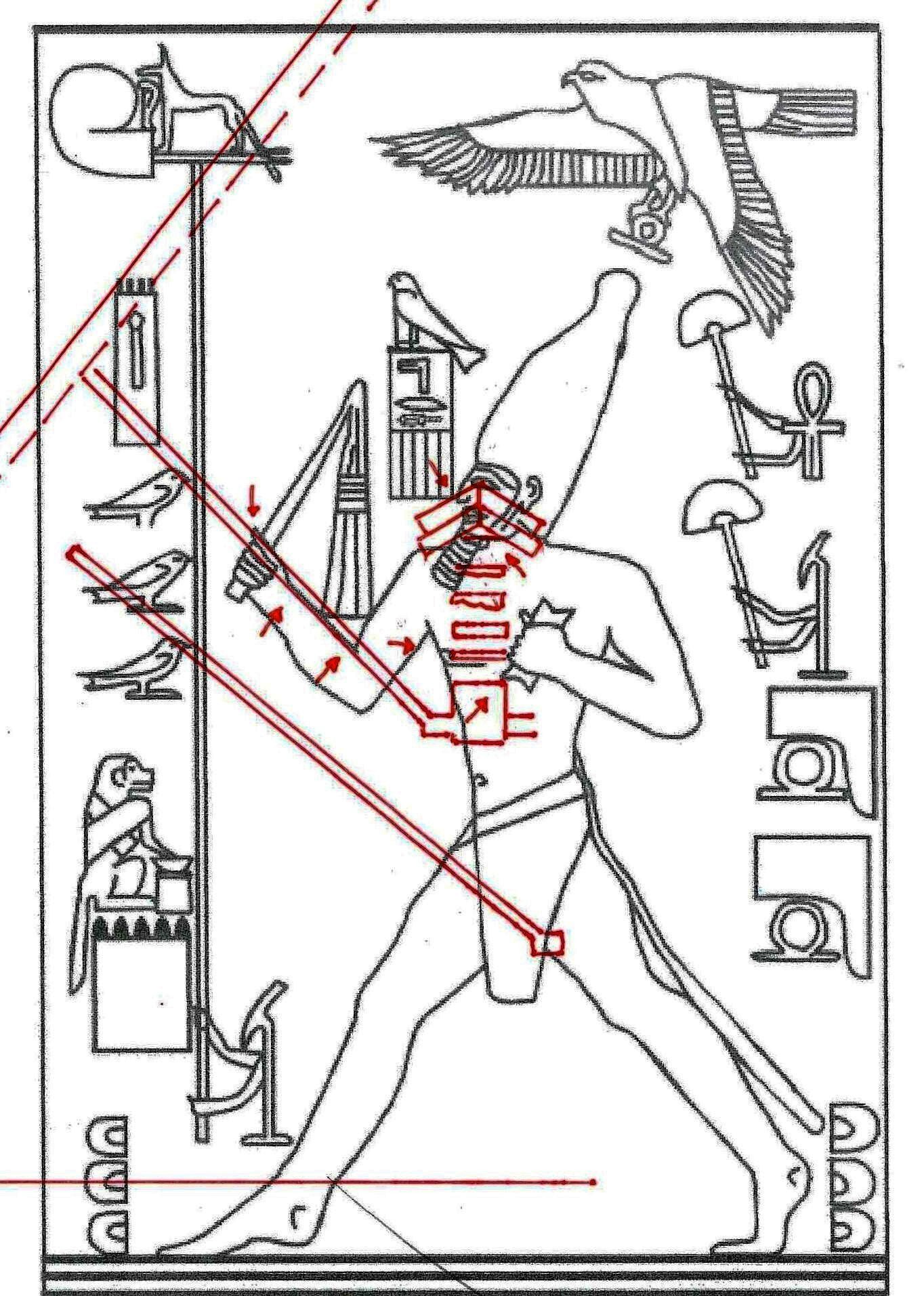
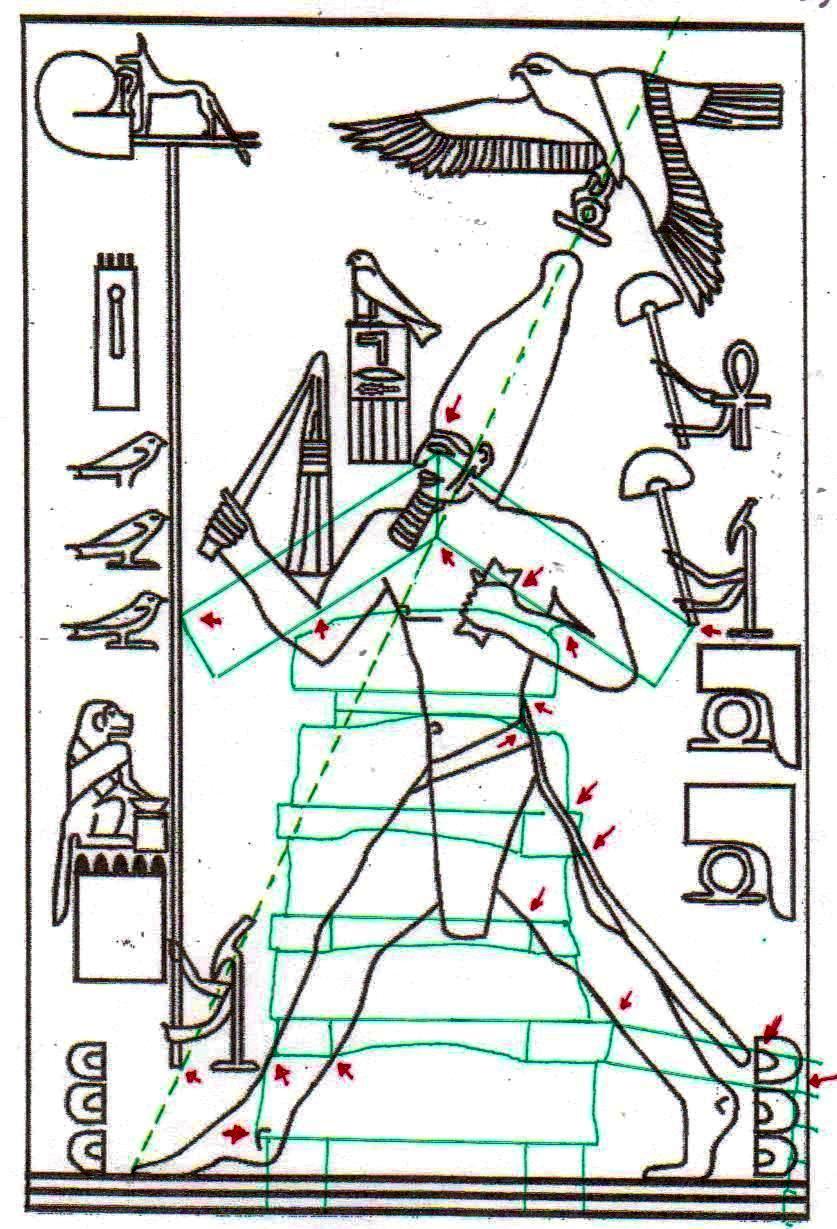
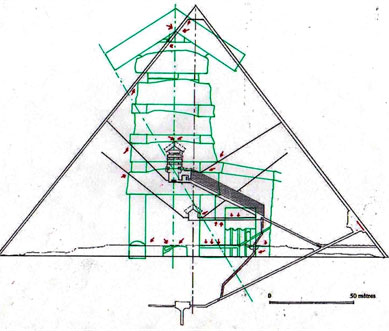
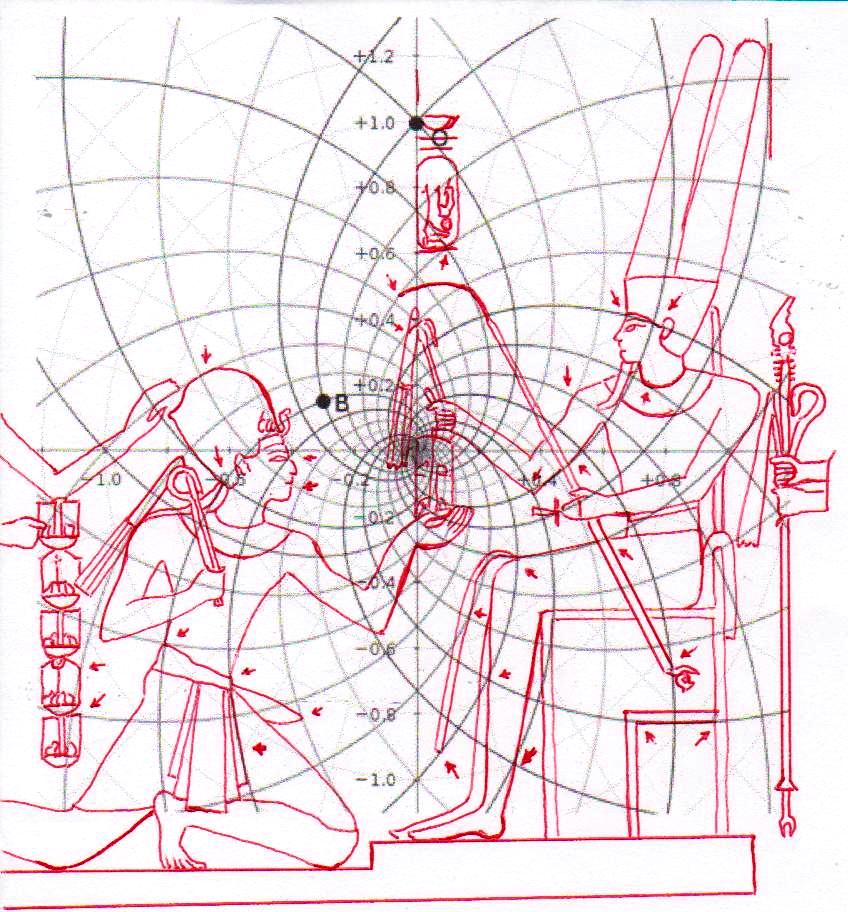
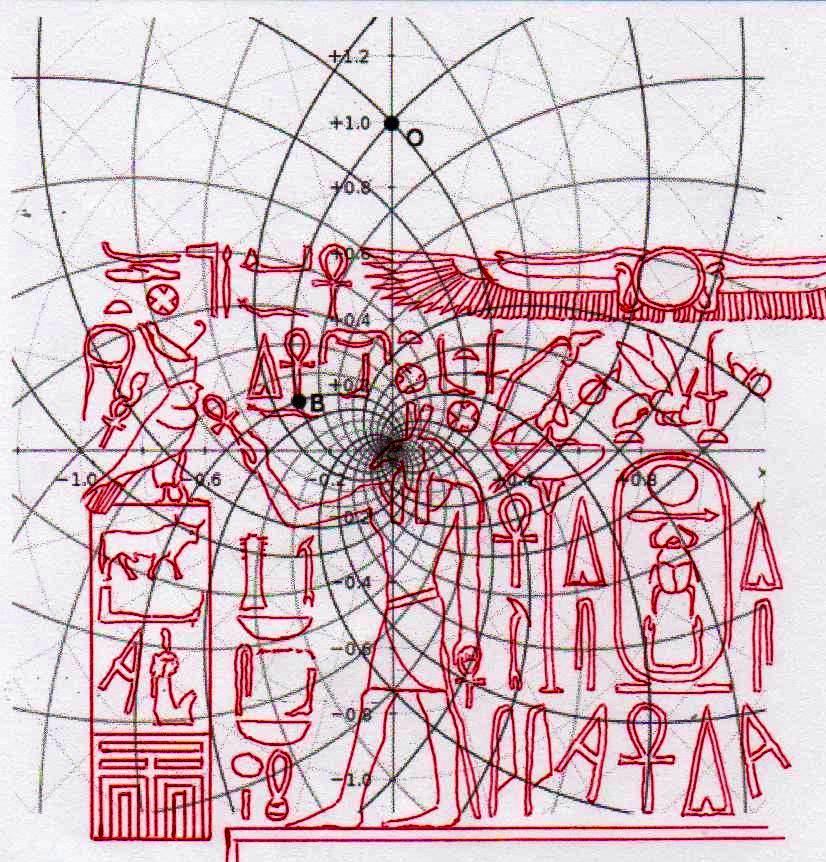
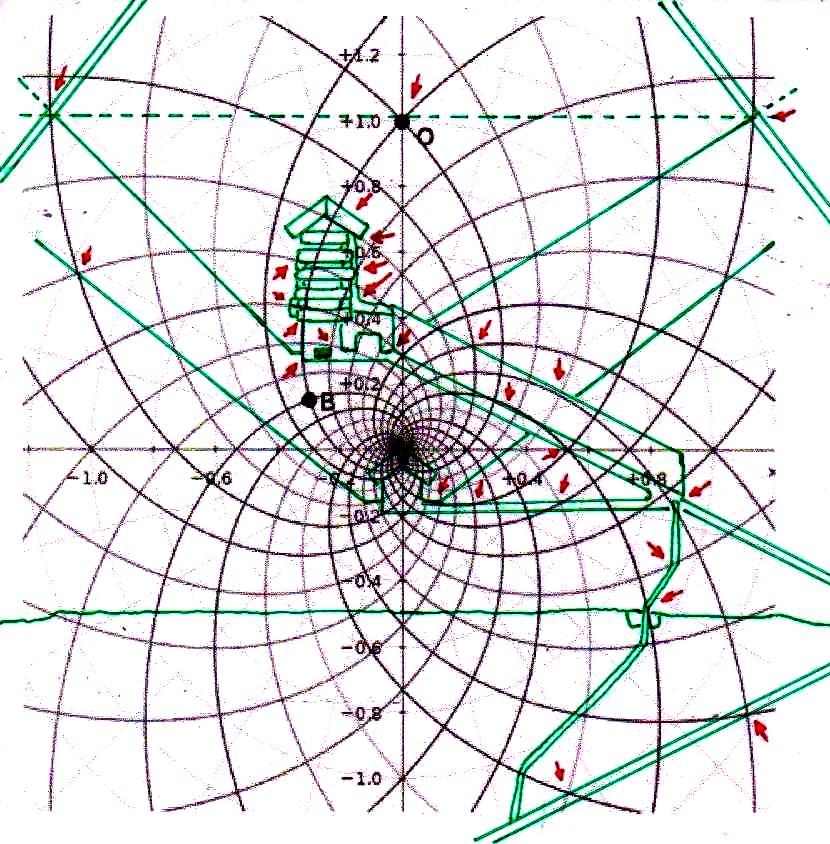
2) Pero, además de este y otros casos particulares, que son por sí mismos muy significativos, el conjunto del trabajo ha dado resultados y ha llevado a hipótesis que, a la luz de la visión, por así decir, “oficial” que se tiene del mundo del Antiguo Egipto, se presentan como desconcertantes. Sólo un código común muy complejo puede estar al origen de fenómenos geométricos como este. Pero ¿Cuál? Después de varios intentos fallidos, parecía que este código podría coincidir con el del diagrama del espacio-tiempo, desarrollado por Vincenzo Fappalà y publicado en ASTRONOMIA.com, basado en la serie de Fibonacci. Apoyado en el centro del relieve de Ramsés y en el eje central de la Gran Pirámide – a la altura del punto de salida de los conductos de ventilación de la Cámara del Rey – lo que podríamos llamar su “ritmo geométrico” parecía coincidir perfectamente con el de las manufacturas del Antiguo Egipto. Tal vez sea bueno refrescar un poco la memoria y mirar estas imágenes junto con otras que hasta ahora no hemos mostrado; el conjunto constituye también un buen resumen de la labor realizada hasta el momento.

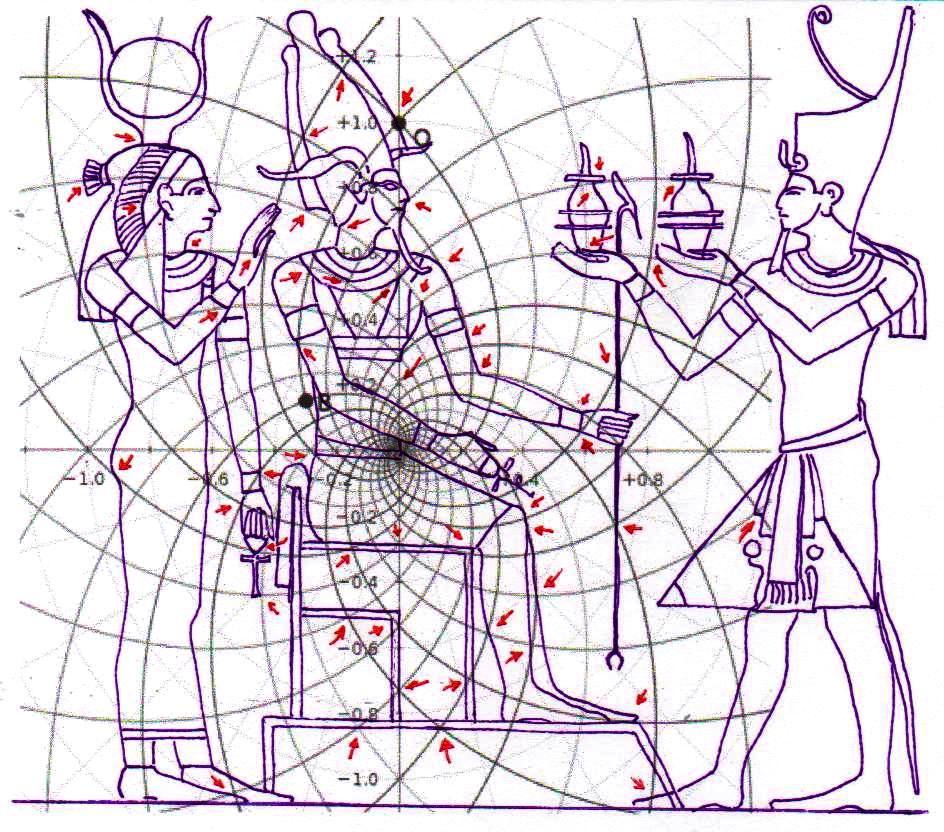
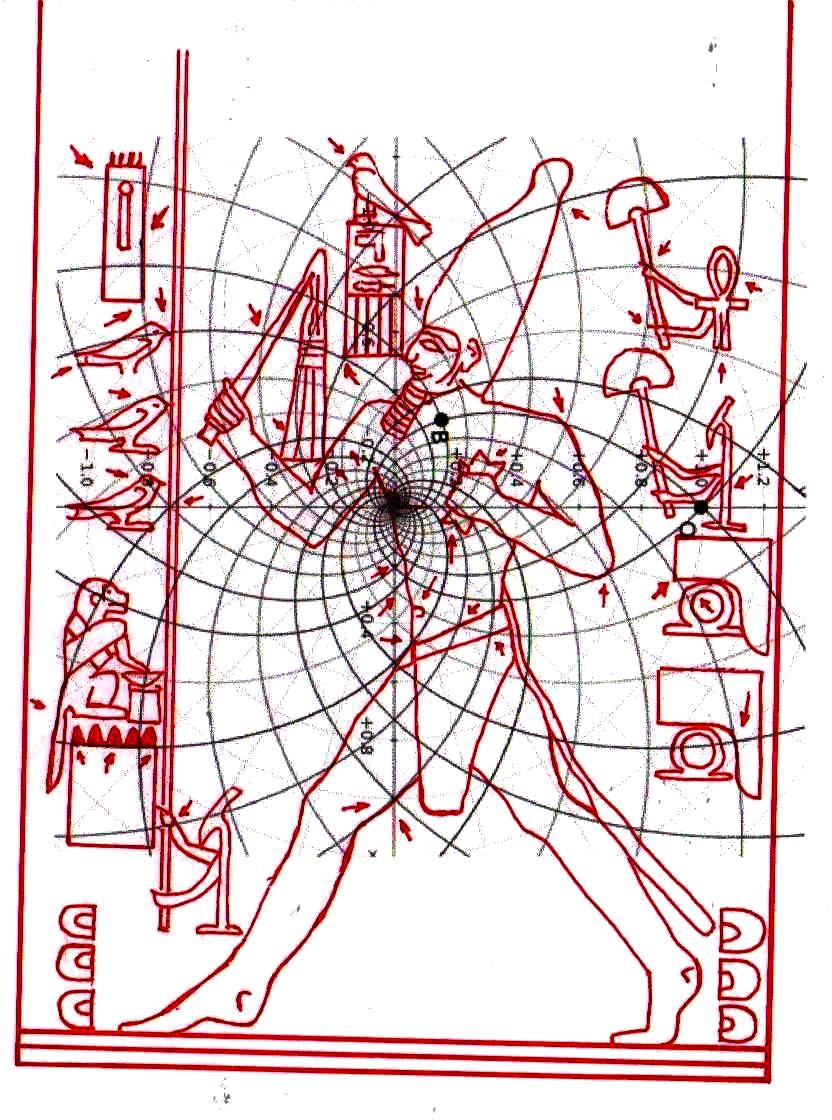
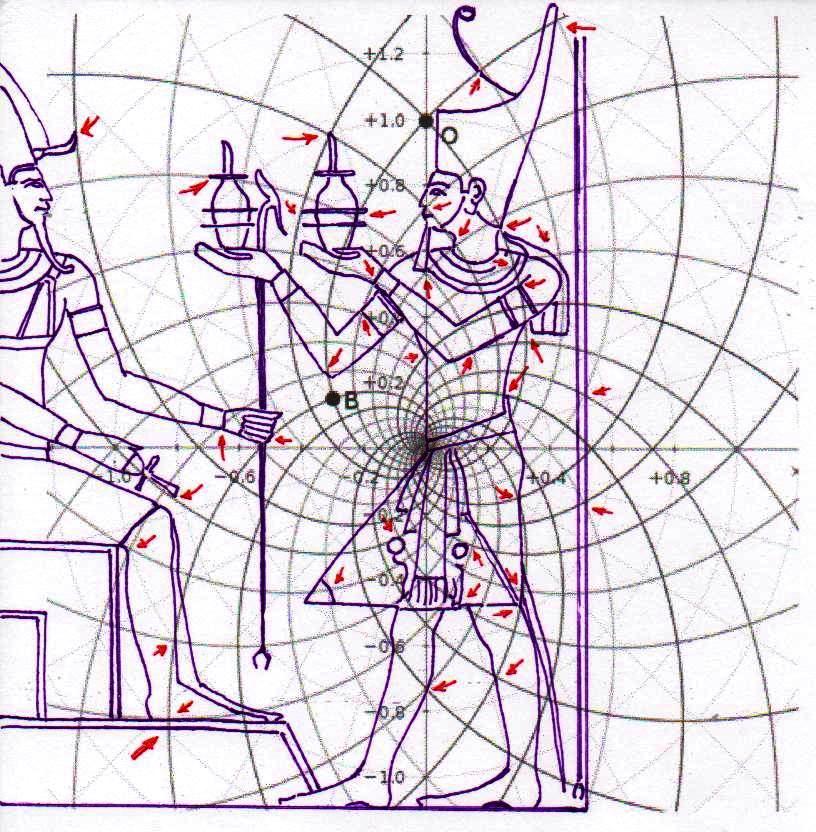
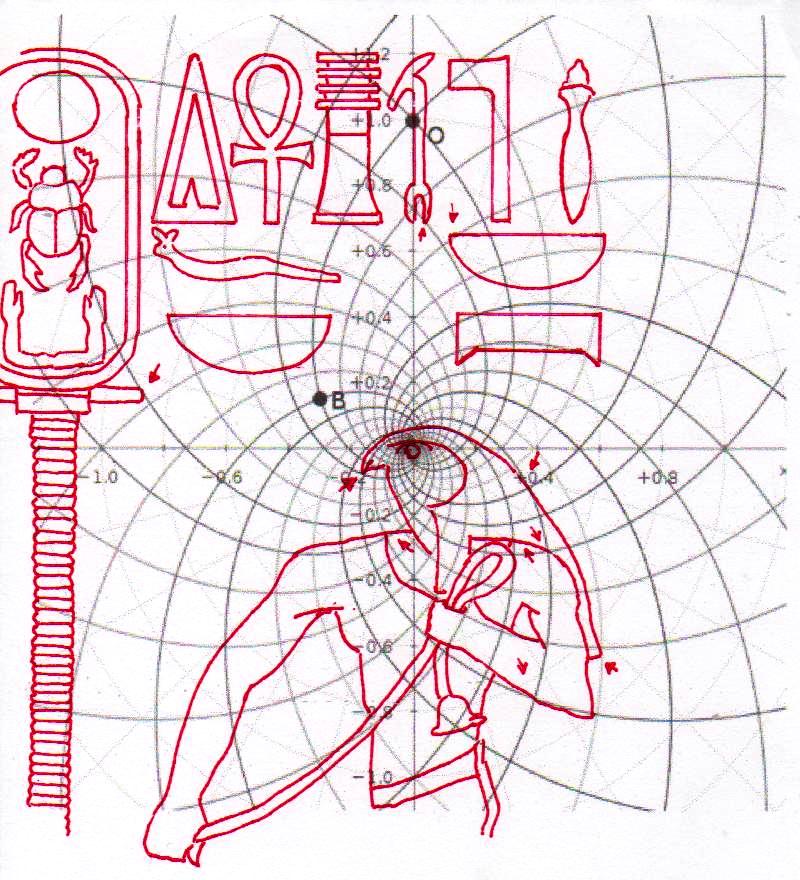
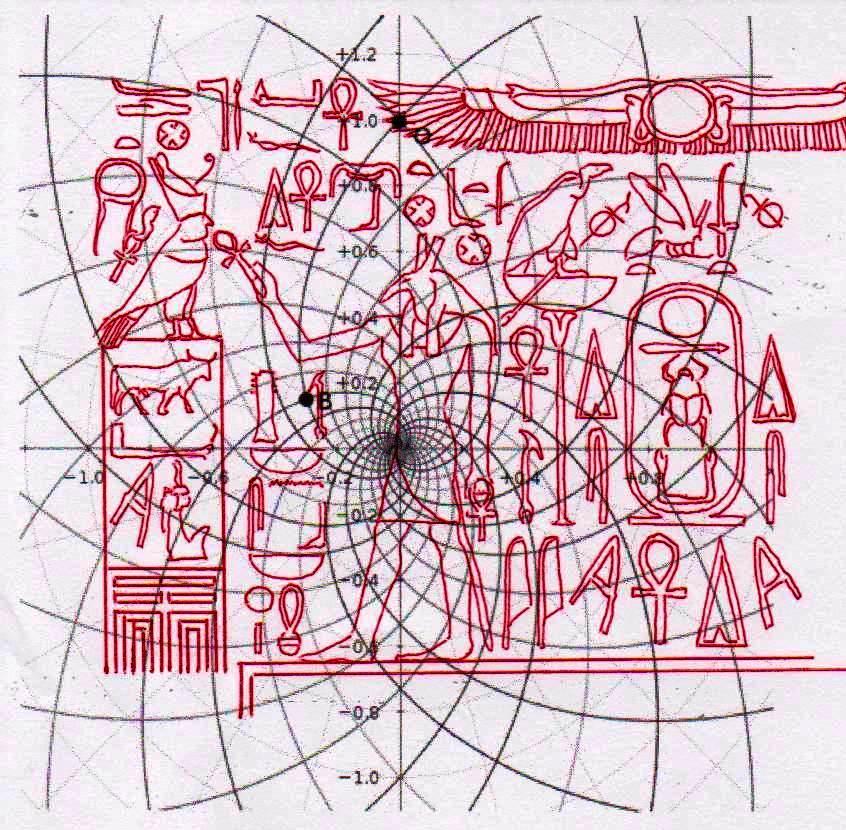
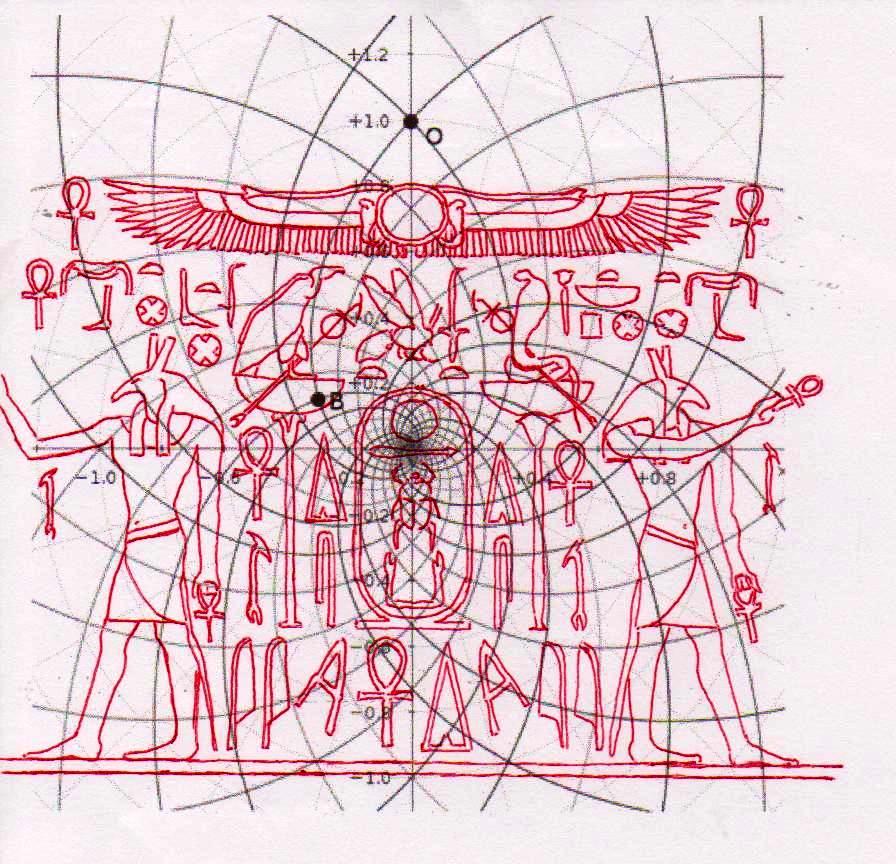
Si el lector quiere ver en detalle nuestra hipótesis para explicar el funcionamiento de este extraño tipo de espacio espiral, puede leer la tercera parte de este trabajo (The Snefru Code part. 3: “El espacio áureo en el arte figurativo y la arquitectura del Antiguo Egipto: una hipótesis de solución a partir de la estructura de la inflorescencia del girasol”). Aquí, por razones de espacio, sólo resumimos en seis puntos claves la interpretación propuesta que allí hemos dado:
1) cada parte de cada forma y figura – tanto iconográfica como arquitectónica – está en una relación áurea con el conjunto del que forma parte y con todas las demás partes
2) esto sucede porque los puntos no son generados por medio de coordenadas obtenidas a partir de un sistema de ejes cartesianos, sino por un sistema de círculos y espirales logarítmicas como el que hemos visto en las imágenes de arriba
3) para obtener un espacio en el que los puntos están cerca uno del otro de manera suficiente para conseguir imágenes complejas, se debe suponer que los puntos se generan a partir de una multiplicidad de polos
4) pues, los polos de expansión de estos vórtices de círculos y espirales logarítmicas deben distribuirse de tal manera que en todo el espacio pueda encontrarse una justa distribución de puntos justamente cercanos – puntos cuyas coordenadas siempre y de todas maneras resultan por el cruce por lo menos de dos espirales o de un círculo y una espiral
5) sin embargo, hay que imaginar que en el progreso de la subdivisión y por lo tanto de la multiplicación de los polos el número de círculos y espirales que se sobreponen en cada punto puede crecer de manera incluso vertiginosa. Lo más probable es que cada punto de este extraño tipo de espacio – que espontáneamente se podría definir como un vórtice de vórtices – hay de pensarse finalmente como un polo de expansión de círculos y espirales logarítmicas, y las líneas trazadas sean a su vez segmentos de círculos y espirales
6) esto significa que, si se mueve el diagrama en diferentes puntos de la figura generada, se encuentran todavía otros sistemas de relaciones áureas. En particular, si se apoya un segmento de diagrama a un segmento de la línea del diseño en el que éstos coinciden, habría que encontrar el centro desde el que se trazó el segmento. Por lo tanto, también todos los puntos identificados por las líneas del diseño están en relación áurea con los demás puntos, aunque de una manera muy complicada.
Hay que reconocer que esta última afirmación no está probada por las imágenes que hemos visto hasta el momento. Pero en breve veremos otras en que podremos reconocer (así creo) de manera suficientemente clara el fenómeno en cuestión.

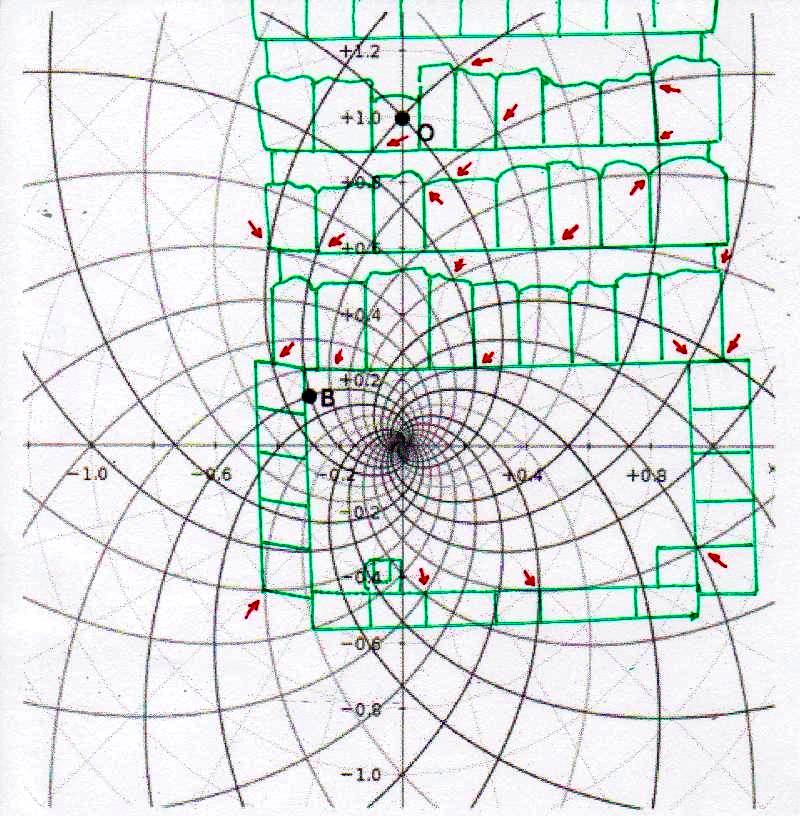
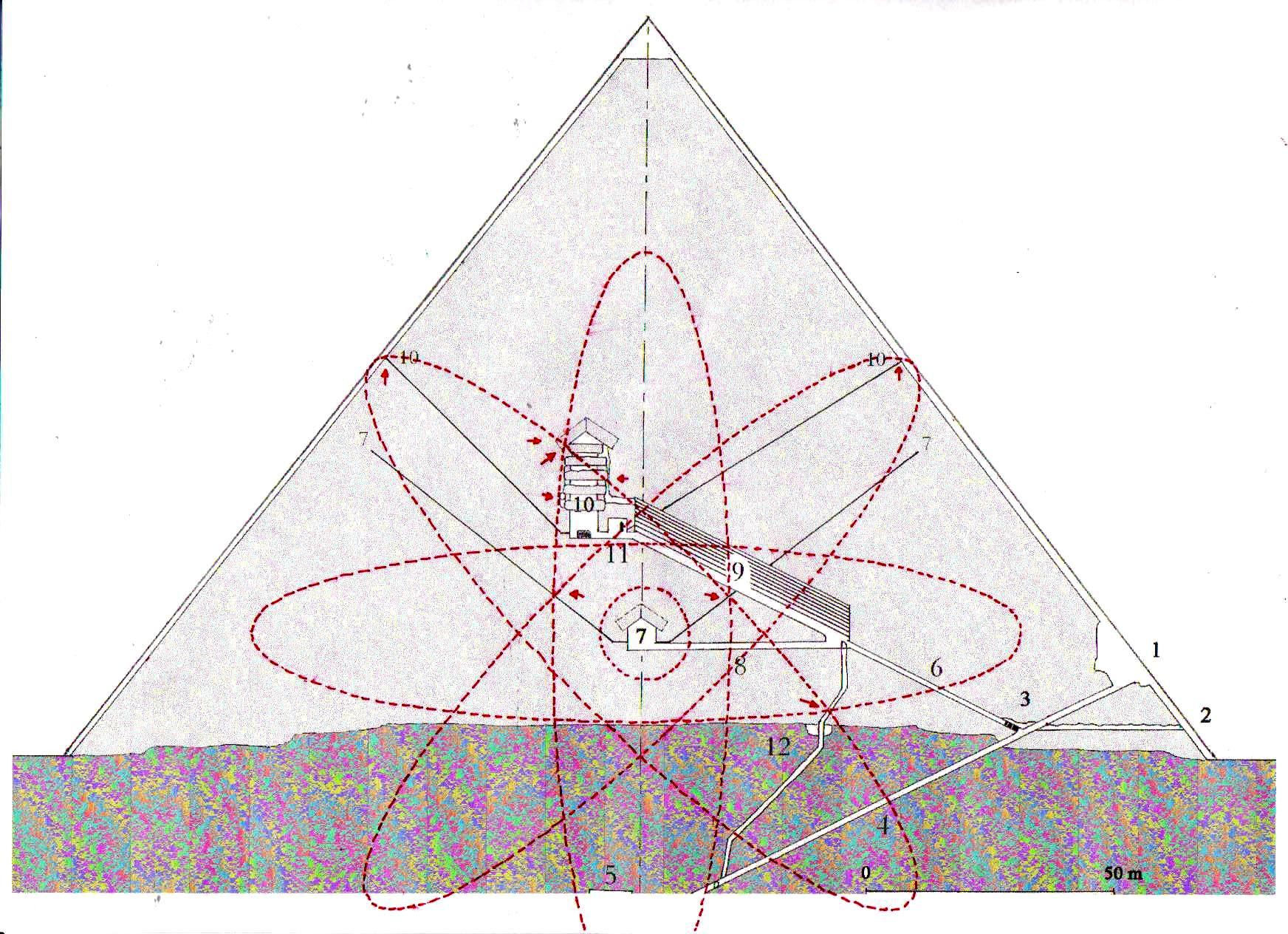
3) Antes de seguir adelante en nuestro argumento es correcto, sin embargo, advertir al lector de que desde más de un siglo hay un debate en curso entre los que atribuyen a los antiguos Egipcios una civilización científica y tecnológicamente avanzada (éstos son los egiptólogos que son definidos y se definen a sí mismos “independientes”) y los que, en cambio, piensan que era un pueblo atrasado, tal vez artísticamente dotado, pero con matemáticas un poco más altas que las que se enseñan en nuestras escuelas primarias. Se trata, en este último caso, de profesionales que pertenecen a la cultura oficial, profesores de las universidades públicas, expertos de museos o instituciones muy importantes. Éstos, frente a los fenómenos geométricos que hemos visto y a las hipótesis basadas en ellos, objetarían que todo lo que se ve en las imágenes no es más que el resultado de un caso. Tomemos, por ejemplo, los más que treinta puntos de intersección significativos que se pueden fácilmente identificar en la imagen en la que el diagrama del espacio-tiempo se ha sobrepuesto a la sección de la Gran Pirámide: los expertos ortodoxos dirán que todo eso es el resultado sin embargo sorprendente de un montón de accidentes fortuitos, de inexactitudes de medición o representación, y cosas de este tipo. Sin embargo, si nos fijamos en la imagen podemos ver que el código geométrico sobre el cual fue diseñada la Gran Pirámide parece desvelarse, ya que a partir del diagrama de Fappalà, podemos reconstruir su ángulo de base, la posición de la Cámara del Rey y la Reina, el principio y el final de la Gran Galería y su inclinación, el punto de su intersección entre el Corredor Ascendente y el Descendente, la altura del montículo de piedra incorporado en la estructura, la posición e inclinación de los dos pozos de la Cámara de Rey y todavía otros detalles arquitectónicos de la estructura. Todo esto debería ser suficiente para descartar que el sistema de “superposiciones significativas”, que podemos encontrar entre la Gran Pirámide y el diagrama de Fappalà es el resultado de algo que no sea lo que podría llamarse un “diseño inteligente”. Para dar al lector una idea clara y distinta de lo que significa explicar con el caso los efectos geométricos del código en cuestión, en las imágenes de abajo cambiamos la escala de la superposición y movemos el diagrama del espacio-tiempo a otros puntos más o menos característicos de la Gran Pirámide. Al hacerlo, nos daremos cuenta de inmediato de que – como hemos dicho anteriormente en el punto 6) – el sistema de las superposiciones, lejos de tener que ver con un cualquier tipo de acontecimiento fortuito, en cambio se recrea inexorablemente de nuevo, tal como lo habíamos visto suceder en el caso del relieve de Ramsés (el lector puede encontrar las imágenes de lo que se trata en el Apéndice fotográficas de The Snefru Code part. 4); lo que demuestra de una manera que parece inequívoca la presencia de una matriz geométrica de la cual se derivó el diseño de la Pirámide.

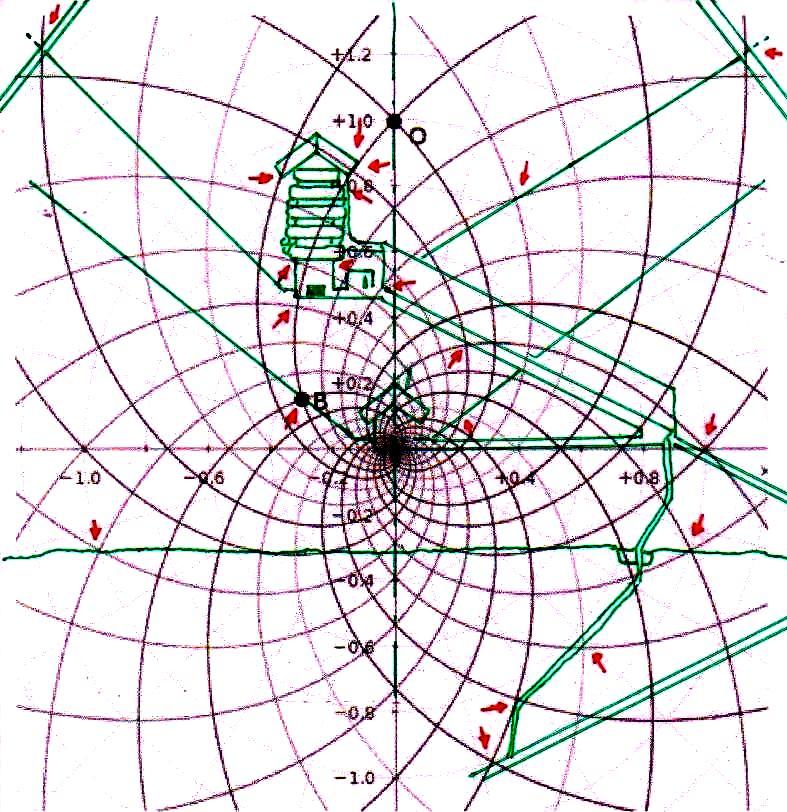
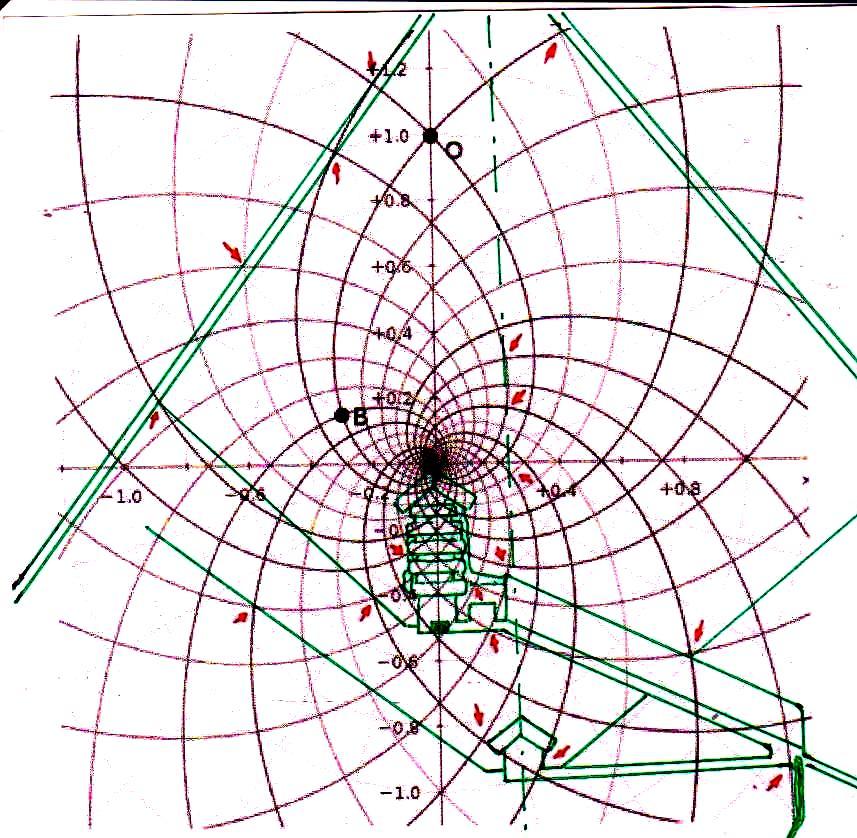
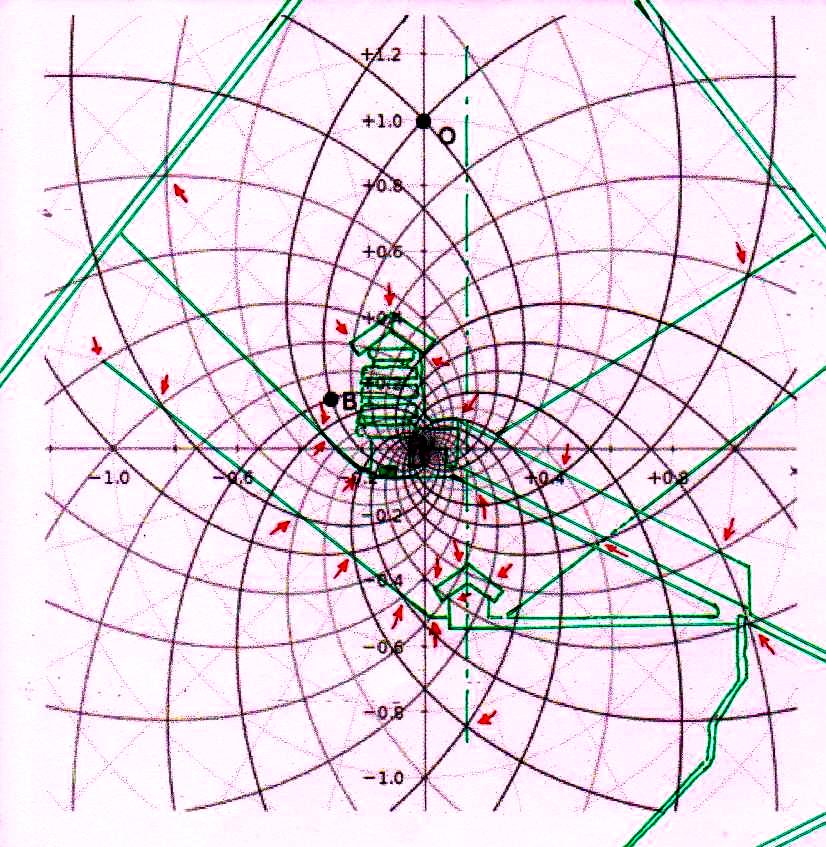
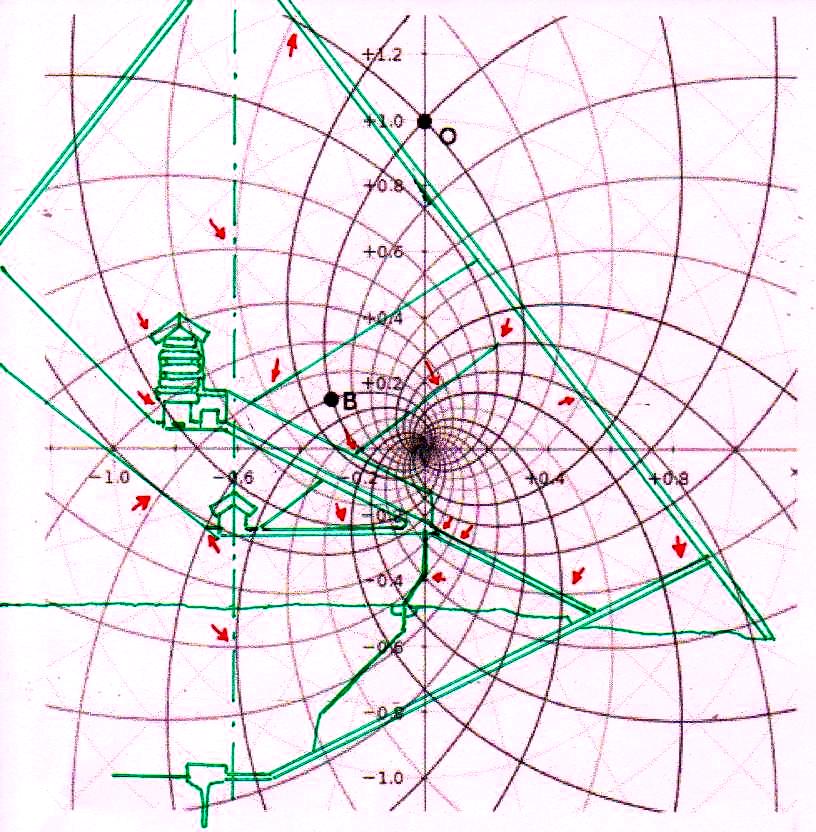
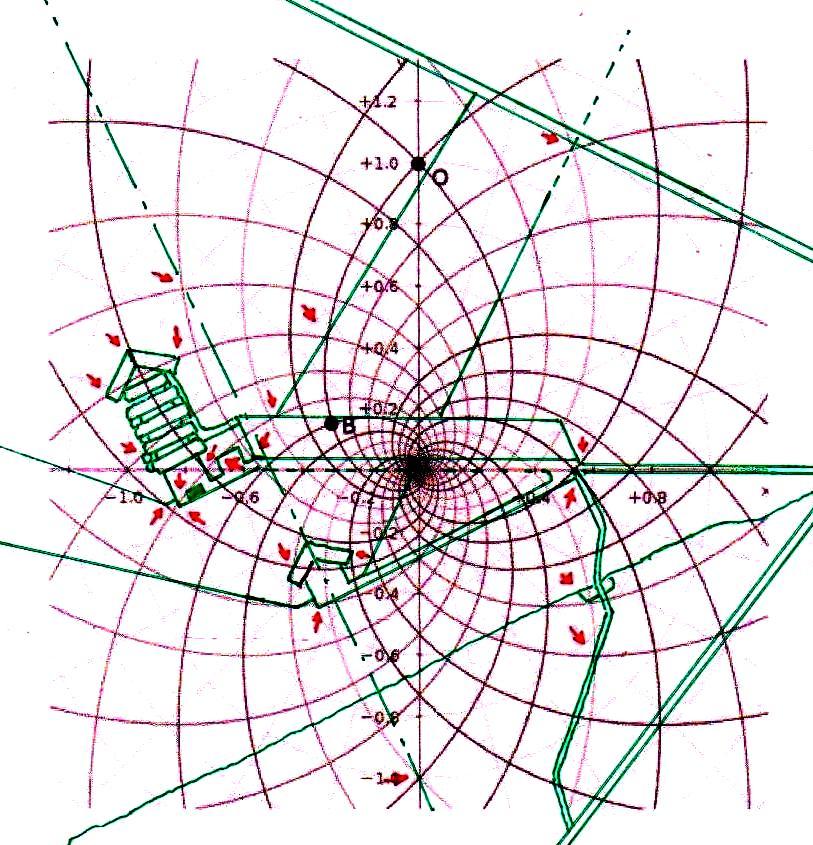
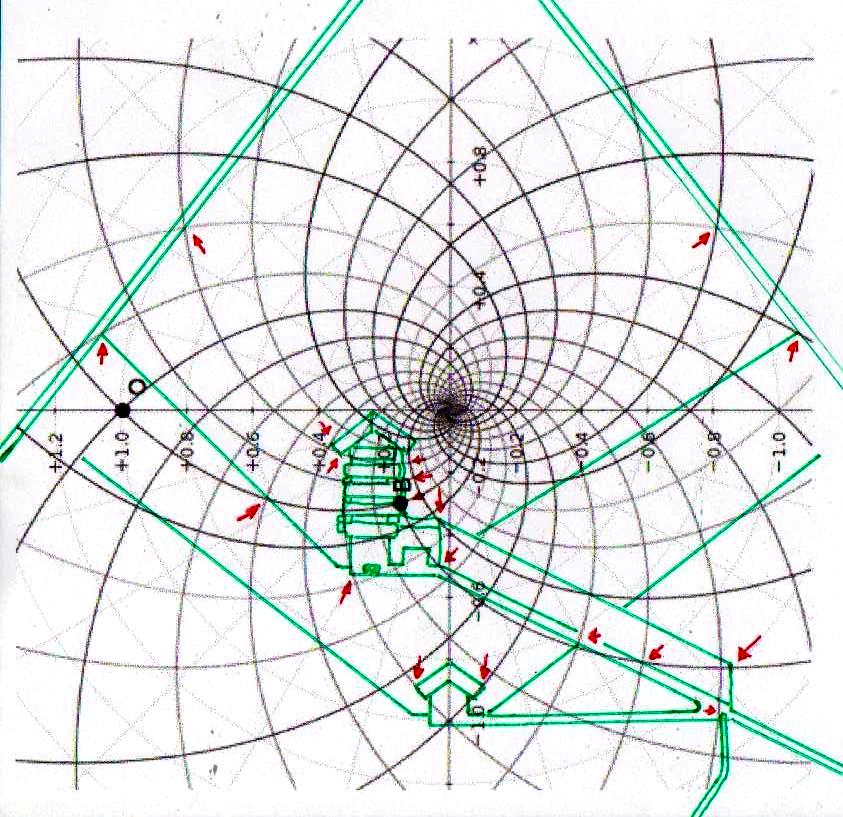
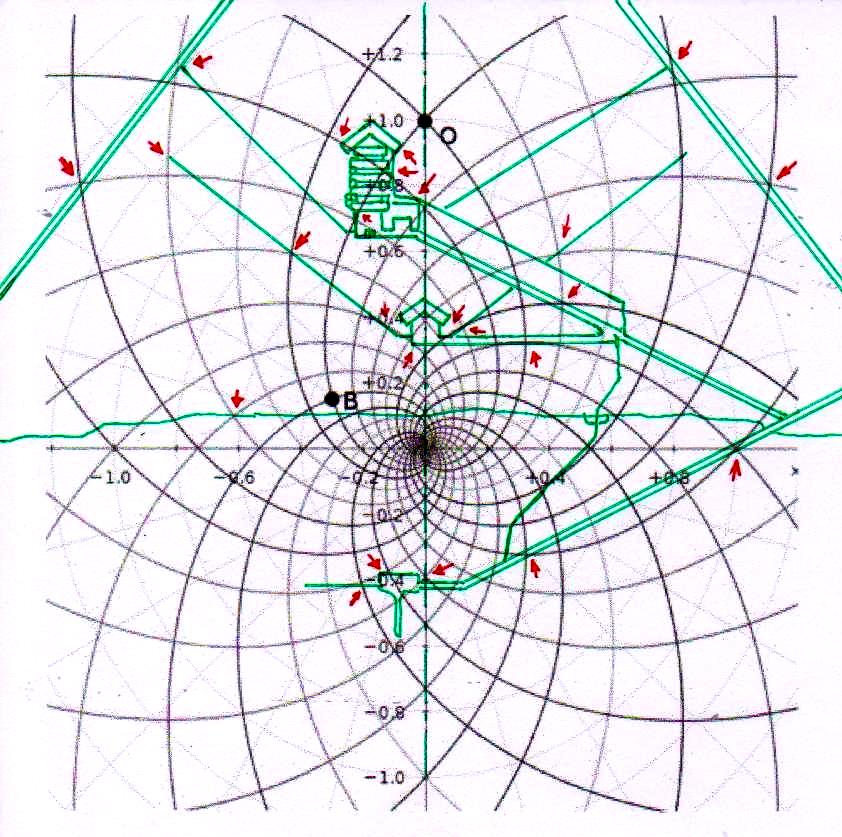
4) Estas imágenes de por sí son bastante impresionantes. Pero aún más impresionante es lo que descubrimos si profundizamos nuestra investigación y nos acercamos a los detalles más menudos de la construcción. Si superponemos el diagrama del espacio-tiempo a la Cámara del Rey, nos damos cuenta de que también esta estructura interna muy importante ha sido diseñada a partir desde la misma matriz geométrica con la cual parece haber sido diseñado el complejo de la Pirámide, hasta el punto de que incluso el tamaño de cada piedra parece responder a un diseño hecho a partir del mismo tipo de espacio. Y eso no es todo. Aunque parezca increíble, observando cuidadosamente las imágenes, parece que podemos decir que incluso los elementos desde siempre creídos sorprendentes defectos de acabado en un edificio tan perfecto (el piso de todas las Cámaras Superiores que a primera vista parece bruto y áspero, el ángulo del sarcófago que parece deteriorado, el contorno del complejo de la estructura de la Cámara del Rey que parece dejado justo al azar, etc.) son también los que, para decirlo así, son deducibles del sistema de círculos y espirales logarítmicas elaborado por Vincenzo Fappalà. Todas las imágenes que siguen, pero sobre todo las dos primeras, parecen ser pruebas inequívocas

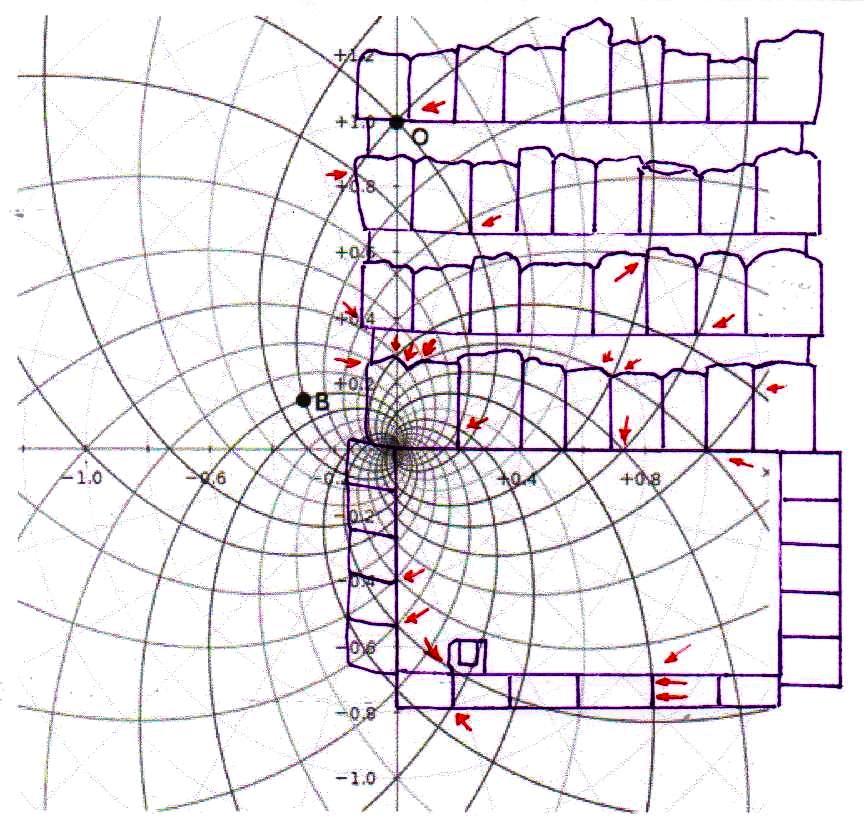
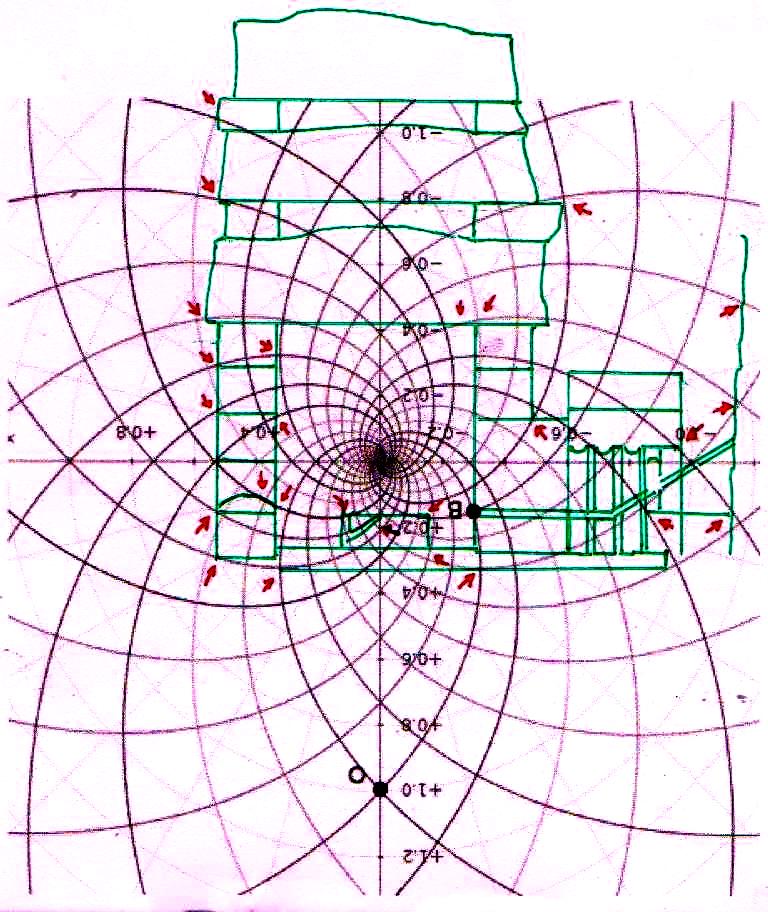
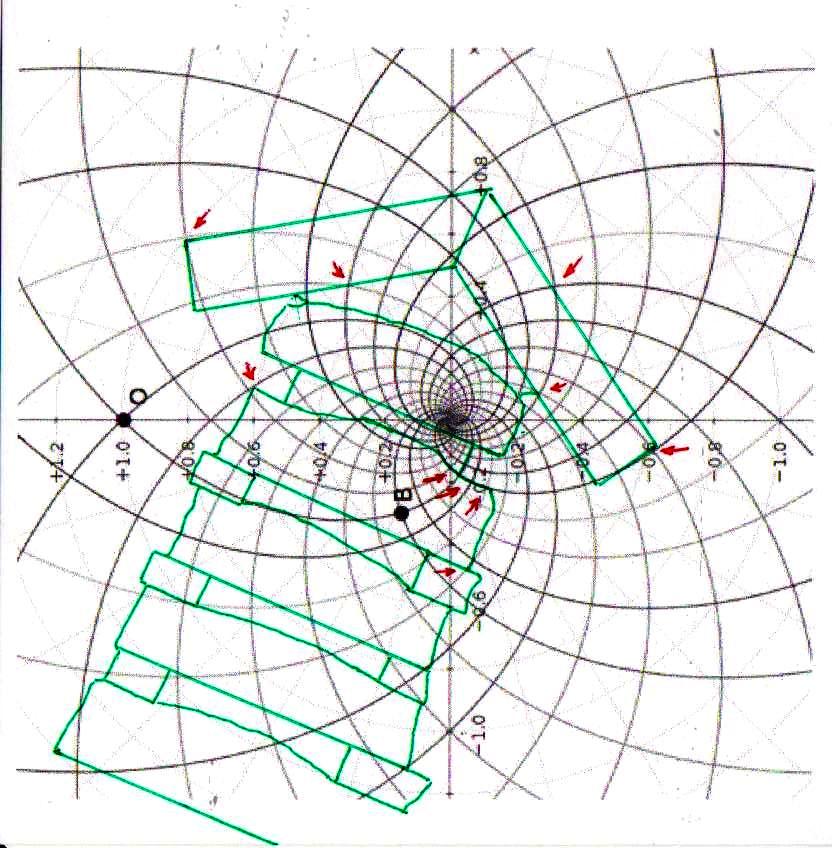
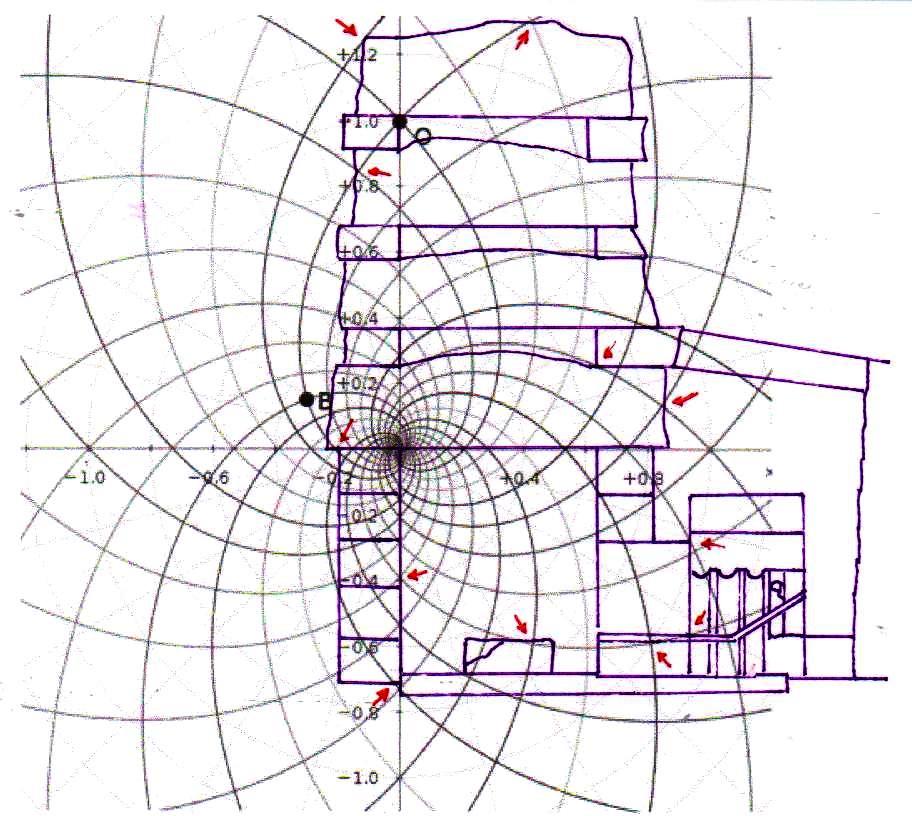
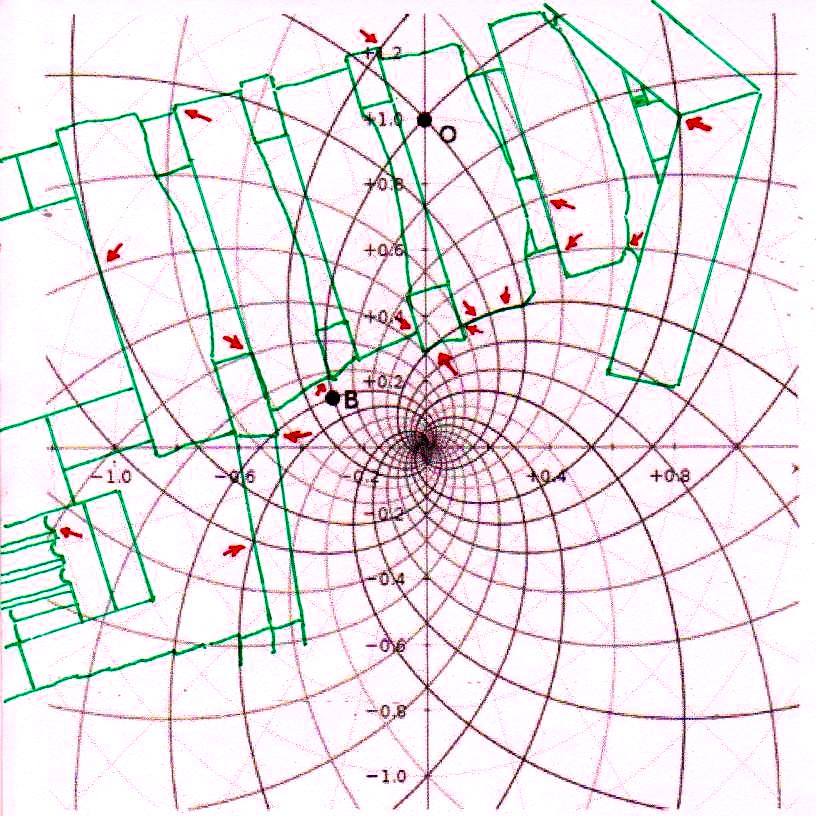
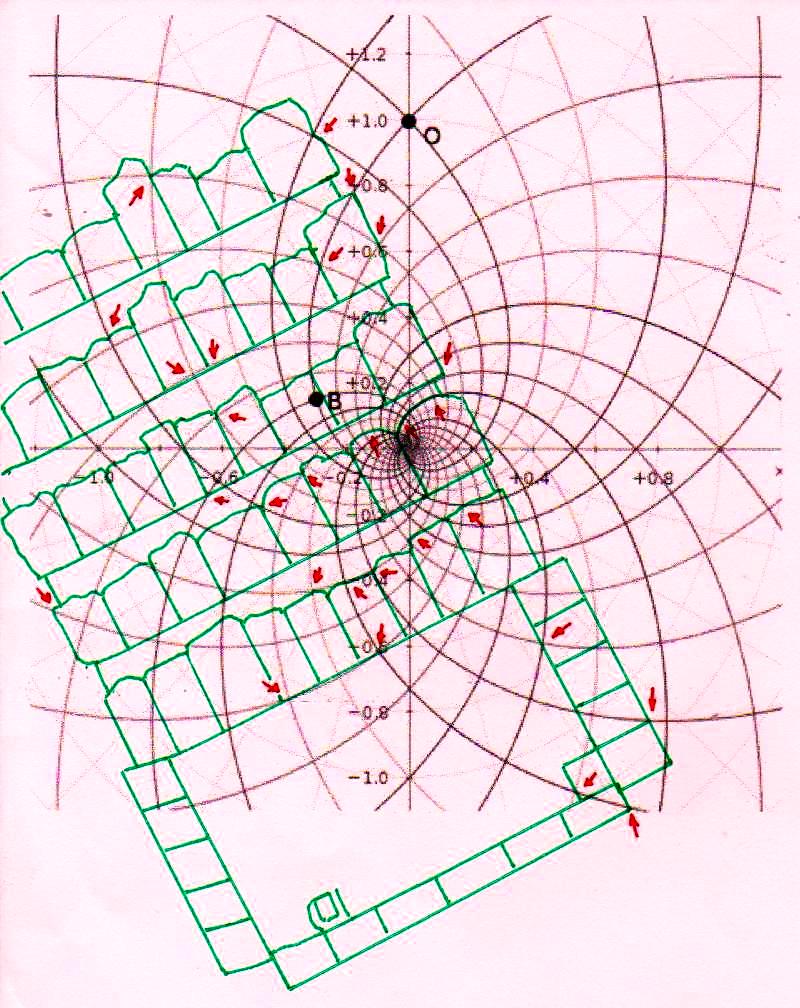
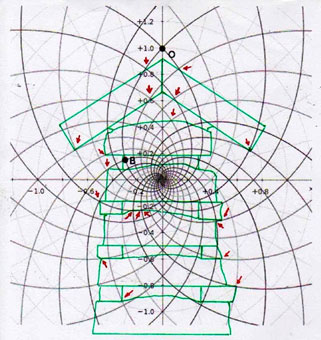
El sistema de las superposiciones, como ahora será incluso previsible, sigue ocurriendo también a nivel de la Cámara de la Reina. Y en realidad seguimos siendo desconcertados frente a estos fenómenos, ya que parece bastante claro que un espacio de este tipo no se puede concebir de manera abstracta y sólo en teoría. Ya incorporar en un solo edificio un sistema de alineaciones astronómicas, como el que realmente ocurre en la Gran Pirámide, parece en sí mismo una extraordinaria hazaña. Pero a esto hay que añadir el hecho de que estas alineaciones están relacionadas con la sección áurea del ciclo de precesión y que se llega a esto siempre y de todas maneras utilizando los ángulos de Orión. Se trata pues de un conjunto de dificultades que transforma el proyecto en algo que parece casi inhumano (para ver estos problemas en los detalles enviamos al lector a The Snefru Code part. 5: “Los ángulos sagrados de Orión y el número de oro en la arquitectura de la IV Dinastía: algunos posibles desarrollos de la reconstrucción arqueoastrónomica de Robert Bauval”). Ahora estamos casi obligados a concluir que, además de todo esto, un código tan complicado como el del espacio-tiempo fue utilizado ampliamente, hasta en los mínimos detalles de la estructura. Y en este punto nos vemos constreñidos a asumir que el proyecto debería haber requerido algo así como un ordenador, tal vez de concepción totalmente diferente de los nuestros, porque una tarea de este tipo parece sin duda ir más allá de las posibilidades de cálculo de los seres humanos al menos tal y como los conocemos hoy en día

Después de un cuidadoso análisis de estas imágenes apenas se puede mantener todavía dudas sobre uno de los objetivos fundamentales para que fue construida la Gran Pirámide. Como nos dice la tradición copta, ella fue por sus constructores un gigantesco libro de piedra, en el que, a través de las medidas generales (pero casi seguramente también a través de las de las piedras que forman el revestimiento de las estructuras internas y las que un tiempo formaban el revestimiento externo del complejo de la estructura) se ha codificado una gran masa de datos científicos y matemáticos. Desafortunadamente, sin embargo, la investigación está todavía en su infancia y es probable que tome décadas para descifrar y comprender este extraño manual que, a primera vista, parece tratar de física y de astronomía utilizando un lenguaje de la alta geometría. Tampoco se puede afirmar que incluso largos o muy largos esfuerzos – aunque fuera de la parte de toda la comunidad científica – estarán en condición de comprender plenamente todo lo que ha sido escrito allí.

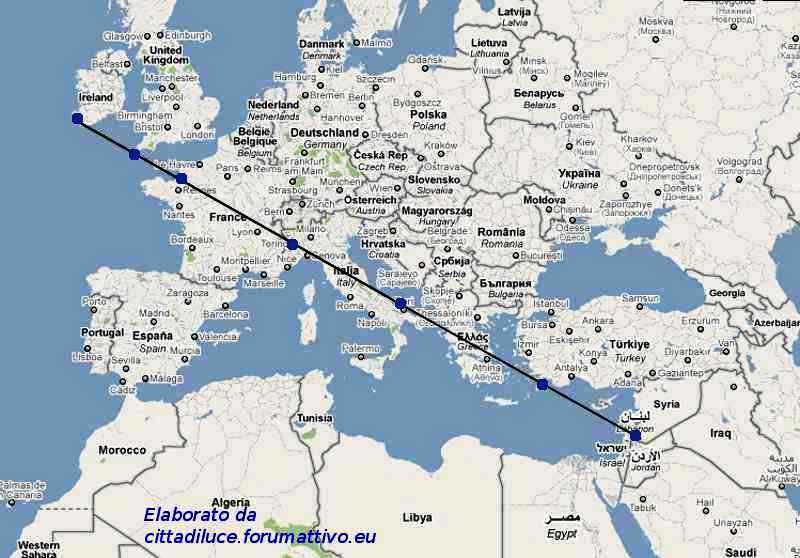
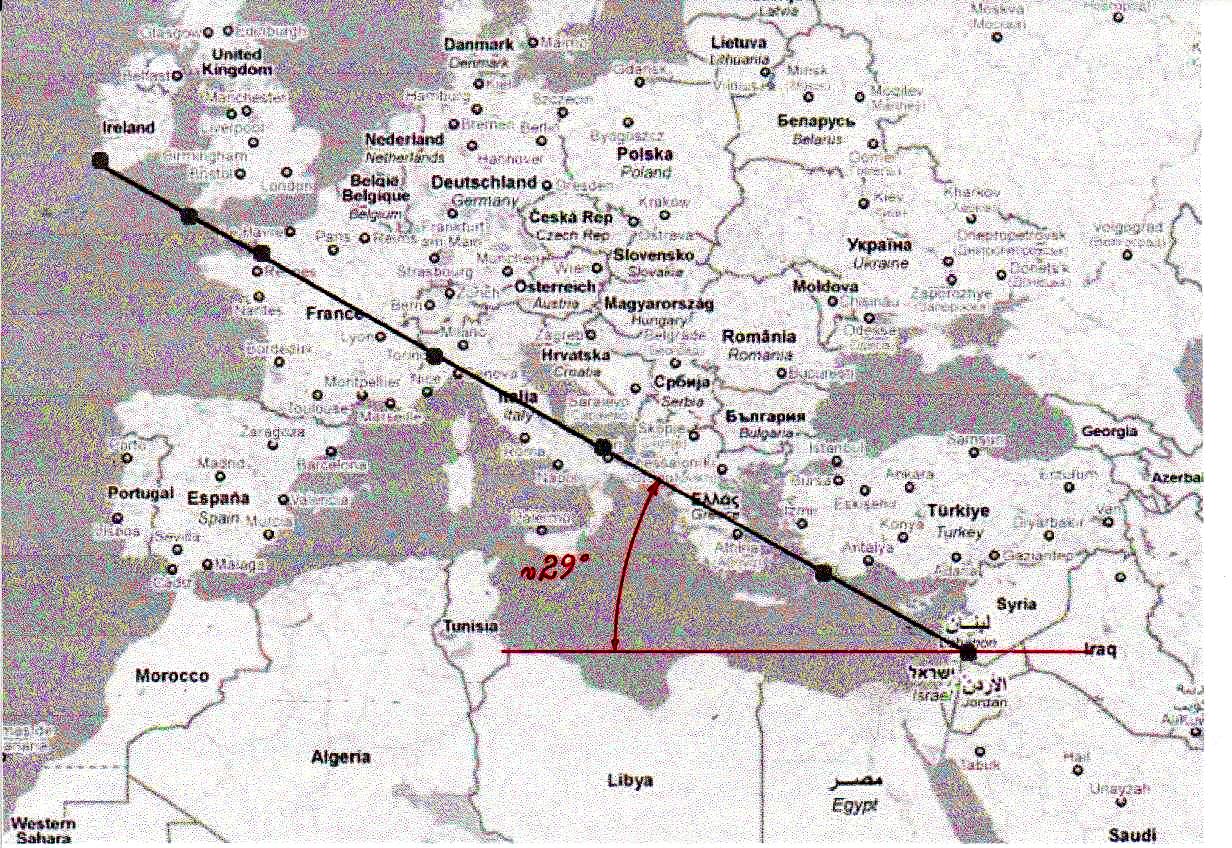
5) Pero, después de toda esta profusión de matemáticas y geometría, ciencias que en nuestro mundo son consideradas laicas casi por definición, ciertamente es oportuno una vez más señalar que toda esta inmensa hazaña intelectual, artística y arquitectónica tuvo un profundo significado sagrado. Es un hecho testimoniado por las alineaciones astronómicas con entidades celestes consideradas como dioses y la incorporación sistemática en la estructura de los ángulos característicos de Orión, la constelación que representaba a Osiris, la divinidad de la muerte y la resurrección en el Antiguo Egipto, que era también considerada como el padre divino del Faraón-Horus. Además de estas referencias a imágenes míticas y astronómicas, en el curso de nuestro trabajo hemos visto que tanto en Guiza como en Nabta Playa aparecen orientaciones características que, además de estar conectadas con entidades celestes en sí y por sí, parecen obviamente relacionadas con el número de oro. De lo que hemos deducido que también ellas deben tener un profundo significado religioso y justo como entidades matemáticas. Decimos esto porque en The Snefru Code part. 4 encontramos que el número de oro caracteriza de una manera que parece indudable tanto el ciclo anual como el de la precesión del Sol, no menos que el ciclo de retrogradación de los nodos de la Luna. En ese mismo trabajo hemos aducido también indicios muy importantes que este ciclo lunar estuvo representado en un diagrama de horizonte totalmente parecido al nuestro, pero que en el contexto de esta cultura servía para dar forma a uno de los tocados faraónicos más común y típico. Esto nos hizo pensar que el número de oro (y justo como entidad matemática) fue visto por los antiguos Egipcios como una parte de la mente de Dios, en cuanto proporción oculta de todos los ciclos fundamentales a través de los cuales la vida es continuamente generada y regenerada por medio de un proceso de nacimiento, muerte y resurrección. A partir de esto, nos dimos cuenta que la proporción áurea de hecho puede encontrarse en muchas alineaciones características de círculos megalíticos o en otros tipos de estructuras sagradas presentes en todo el mundo, además de lo que hemos analizado más a fondo y que estaba en la base de toda la investigación, a saber el Círculo de Nabta Playa. Entre las más famosas estructuras megalíticas hemos indicado las del sur de la Gran Bretaña, sobre todo Stonehenge y Castlerigg. Después, progresando en el análisis de las estructuras de la Gran Pirámide, nos dimos cuenta de un hecho que parece también bastante notable, a saber, que el techo de la Cámara de la Reina tiene una inclinación que parece coincidir exactamente con el sistema de alineaciones que, partiendo de Irlanda meridional en dirección sureste, sigue un eje que pasa a través de dos catedrales muy famosas, Mont Saint Michel y San Miguel Arcángel, y llega hasta Palestina. Esta alineación consiste en instalaciones relativamente modernas, iglesias y catedrales, relacionadas precisamente con San Miguel Arcángel, que habría requerido la construcción de tales edificios con apariciones y hechos milagrosos. La inclinación es de aproximadamente 29°, una inclinación prácticamente idéntica a la de la sección áurea del ángulo recorrido por la tierra durante la mitad de un ciclo de precesión, lo que equivale a unos 47°. Hay también de tener en cuenta que la distancia entre el punto de partida de esta alineación y San Miguel Arcángel constituye una buena aproximación a la sección áurea de la longitud total de la alineación (alrededor de 1,7 frente a 1,618033).

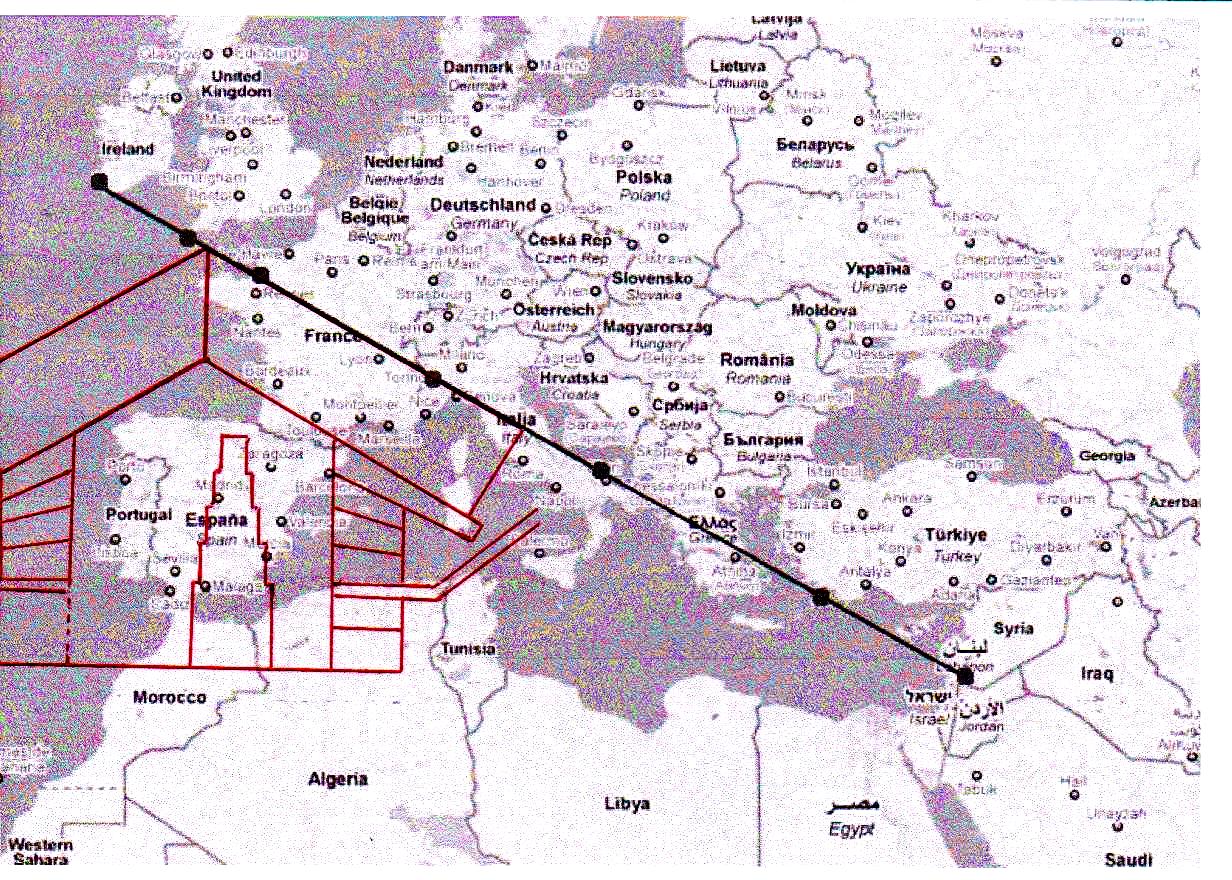
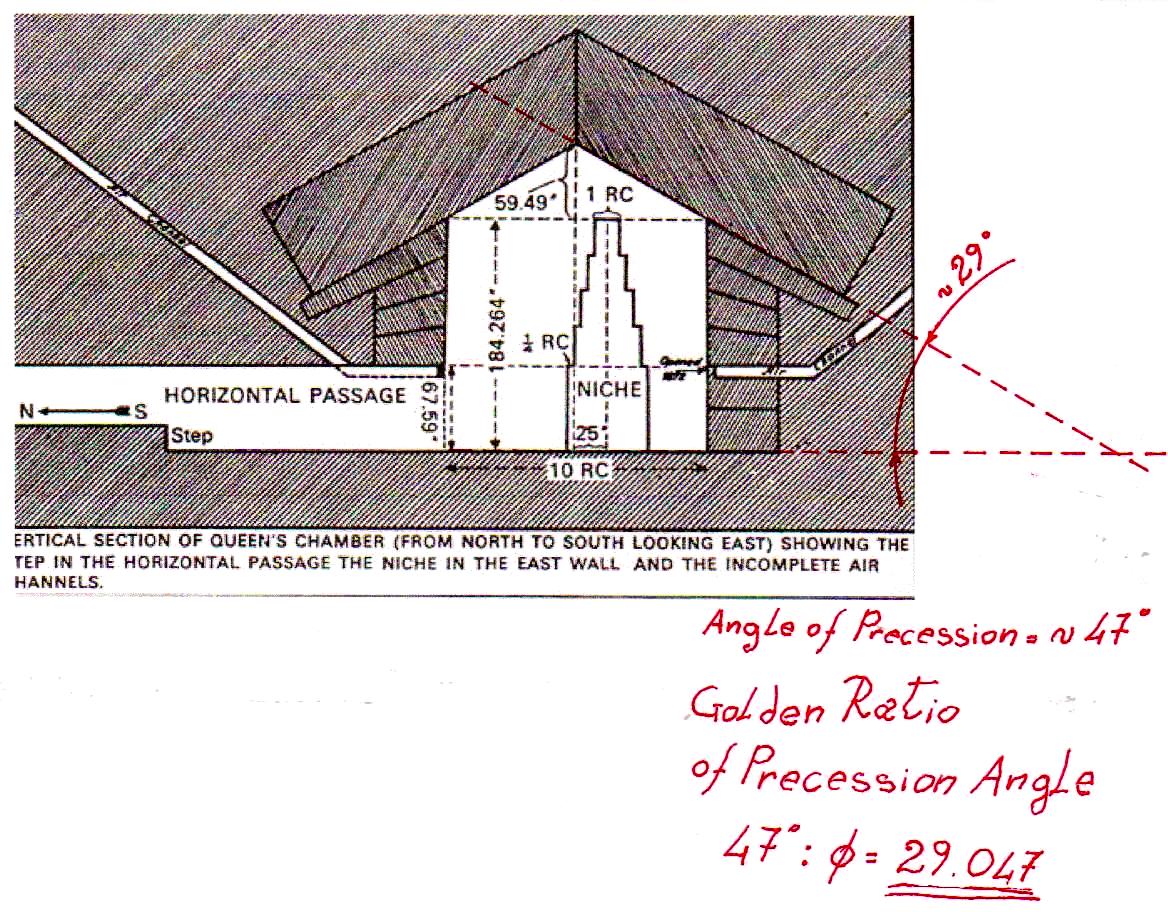
6) Por lo tanto, parece que para comprender el significado astronómico y probablemente también científico de las orientaciones de algunas estructuras construidas en Occidente en la era cristiana hay que remontarse a las orillas del Nilo, a épocas que se hunden en la oscuridad impenetrable de los milenios. Atribuir algo así a una coincidencia trivial parece bastante difícil, sobre todo si tenemos en cuenta que muchas fuentes nos hablan de contactos que hubo en diferentes épocas entre la cultura hebrea del Antiguo Testamento – de la que después han surgido el Cristianismo y los constructores de las catedrales – y la cultura del Antiguo Egipto. En The Snefru Code part. 6 ya habíamos visto que tanto el Círculo de Nabta Playa como la Cámara de la Reina compartían una estructura arqueoastronómica que parece aludir a un ciclo de muerte y resurrección de Osiris; un ciclo que tiene algunas semejanzas características con lo que en la Pascua cristiana se celebra con referencia a la muerte y resurrección de Jesús. No obstante las enormes diferencias teológicas que hay entre los dos, en ambos casos vemos que la resurrección de la divinidad está conectada con la del Sol y por lo tanto con la de la vida natural. A esto podemos añadir ahora que incluso la Cámara del Rey parece tener indudables alusiones a un episodio contado en los Evangelios. Cuando las piadosas mujeres van al sepulcro para ungir el cuerpo del Maestro en la versión de Mateo se dice cómo en el momento de su llegada se produjo un gran terremoto, a continuación llegó un ángel y, descubierto el sepulcro, anunció a las mujeres que Jesús había resucitado: ellas miran y ven que la tumba está vacía. La forma en que se produce la aparición del ángel sugiere que el sepulcro puede estar dañado, ya que un terremoto está ciertamente en condición de quebrar y separar partes de un edificio de piedra. El texto de Mateo también deja un poco de “espacio hermenéutico” para suponer que el terremoto pudo haber sido la forma en la que el ángel quitó la piedra que cubría la tumba. Pero si ahora imaginamos de entrar en la Cámara del Rey, aquí estamos frente a un sarcófago que, al igual que en el caso de la tumba de Jesús, aparece destapado, vacío y dañado (parece que hasta el siglo XIX la tapa estaba junto al sarcófago, luego fue robada en circunstancias poco claras). La semejanza de esta “escena sagrado-arquitectónica” con la del Evangelio es tal que empuja a suponer que su significado puede ser justo el de la ocurrida resurrección de Osiris, que había sido encerrado en el sarcófago por Seth (hay que recordar que en el antiguo mito egipcio es Isis, hermana y esposa de Osiris, que le resucita aleteando; de hecho en muchas representaciones Isis recuerda mucho la figura de un ángel así como a menudo está representado en la tradición iconográfica cristiana). De esta manera sería desvelado el enigma de las llamadas cámaras funerarias y sarcófagos que se encuentran regularmente vacíos. Siguiendo esta línea interpretativa, las cámaras funerarias serían en realidad símbolos de la resurrección, y incluso los sarcófagos vacíos que se han encontrado en varias ocasiones en el Antiguo Egipto seguramente pueden ser considerados como alegorías de la vida eterna a la cual está destinado Osiris, ya que una tumba vacía bien puede representar la victoria de lo divino sobre la muerte. Esta es una hipótesis que se refuerza aún más si tenemos en cuenta todo lo que hemos descubierto con respecto al ciclo anual de la muerte y resurrección de este dios (en particular por lo que se refiere a los acontecimientos astronómicos relacionados con el equinoccio y el solsticio en Nabta Playa).

7) Así que parece que podemos identificar en las Pirámides un arquetipo arquitectónico-astronómico de la escena de la resurrección de Cristo, cuyos orígenes se remontan probablemente a decenas de miles de años atrás, si tenemos en cuenta las conexiones que en The Snefru Code part. 6 hemos identificado entre el mito de Osiris y el significado teológico-astronómico de la Capilla de los Leones y Rinocerontes de Chauvet. A la luz de estas consideraciones el viaje realizado por la Sagrada Familia a Egipto para proteger a Jesús de la furia de Herodes puede tener otro significado más allá de lo habitual. Este episodio evangélico podría aludir a Egipto como tierra donde el nacimiento, la muerte y la resurrección de Jesús fueron prefigurados en una fe ciertamente diferente, pero con rasgos que parecen sustancialmente parecidos a la que había de venir (hay que tener presente que la idea de Maat sin duda tiene algo que ver con la de la Caridad).

SEGUNDA PARTE: RESTOS ARQUEOLÓGICOS Y PREJUICIO HISTORIOGRÁFICO

1) Todos los que son aficionados (por cuanto poco) a la cultura saben que hoy en día las ciencias exactas están apreciadas en sumo grado. Esta estimación llega al punto que no hay ningún campo de conocimiento en el que no se intente imitar o utilizar en una forma u otra los métodos cuantitativo-matemáticos, tal vez incluso de manera completamente improcedente, con el fin de ganar credibilidad y prestigio a los ojos de los intelectuales de otras ramas o incluso sólo del público de media cultura que muestra interés en su tema. Pero, a pesar de esto, el enfoque que se ha dado en las universidades de todo el mundo al estudio de las culturas como la del Antiguo Egipto es precisamente el que ya hemos mencionado anteriormente o sea un rechazo programático de testar de manera científicamente precisa los restos arqueológicos, si exceptuamos las dataciones realizadas al radiocarbono. Esto porque se da por inamovible presuposición de cualquier investigación histórica que estas civilizaciones no tienen nada que ver con las matemáticas y las ciencias matematizadas; y quien piensa lo contrario casi a priori es considerado como una persona que sufre de algún tipo de desviación mental, tal vez leve, que no impide a nadie de desarrollar una vida completamente normal, pero sólo en campos diferentes de el de la arqueología. Así – tal vez para no caer ellos mismos víctimas de aquel plácido sarcasmo con el que se estigmatiza a todos que se alejan de las reconstrucciones oficiales – los arqueólogos oficiales se han cerrado de una manera que parece casi religiosa en la defensa del dogma del atraso científico y tecnológico del hombre del Neolítico, y consideran esa defensa como línea infranqueable de la razón y el sentido común. Pero hay casos en que se utilizan indagaciones cuantitativas para demonstrar lo contrario y tal vez se hace con éxito brillante. Por ejemplo: el trabajo de Christopher Dunn aduce pruebas científicas concluyentes de la existencia de una técnica y de matemáticas de alto nivel en el Antiguo Egipto; y Christopher Dunn es un ingeniero aeroespacial rico y prestigioso, que en sus investigaciones ha utilizado la mejor tecnología que se le ha permitido de la parte de los responsables de los sitios arqueológicos y museos egipcios, y no es un maníaco del fin del milenio, como se ha tenido el coraje de escribir. Sin embargo, la tarea que los arqueólogos y, por lo tanto también los egiptólogos académicos se han atribuido es la de evitar cuidadosamente de tener en cuenta los resultados de esas indagaciones o de considerarlos con ironía indiferente y apriorística. Pero a veces hay excepciones a esta actitud y hay gente que – en vez de callar estas indagaciones (un silencio que otros llaman “censura”) – han hecho experimentos que pueden confirmar los resultados obtenidos por los egiptólogos independientes. Con respecto a esta cuestión aquí vamos a analizar el experimento de Lehner, uno de los mayores arqueólogos responsables del Plateau de Guiza. Lehner ha tratado de demostrar que en realidad se ha podido esculpir la Esfinge con los medios que la arqueología oficial atribuye a los antiguos Egipcios: el martillo de piedra y el cincel de cobre. Vamos a tratar de dar al lector una breve y distinta reseña de este experimento, porque pensamos que es importante que los que leen estas páginas tengan una idea de la manera de proceder de la arqueología oficial cuando intenta demonstrar el fundamento inductivo y práctico-cuantitativo de sus afirmaciones teóricas. En segundo lugar, porque nos imaginamos que frente a una afirmación como “en el Antiguo Egipto se trabajaba la piedra con martillos de piedra y cinceles de cobre”, el lector mínimamente consciente de los problemas asociados con el procesamiento técnico y científico de materiales duros o muy duros, como el granito rosa, el pórfido, la diorita, etc., se estará seguramente preguntando: ¿Cómo es posible que se puedan atribuir prestaciones técnicas de nivel tan inconcebiblemente alto a medios tan poco eficaces, con los cuales no será fácil trabajar materiales más tiernos? Aunque pueda parecer extraño, la respuesta que dan sistemáticamente Lehner y todos aquellos que más o menos piensan como él es que estos medios son los únicos que se han encontrado y – sobre todo – los únicos que están representados en las imágenes sagradas del Antiguo Egipto. Un argumento – éste último – que no aparece particularmente lógico. Si dentro de cinco mil años unos arqueólogos entran en una iglesia del siglo XX y encuentran unas pinturas en las que hay personajes vestidos como en el tiempo en que vivió Jesús, seguramente cometen un grave error si creen que esta era la forma en que la gente se vestía en el tiempo en que la iglesia fue construida. En particular, si en la iglesia hay una pintura en la que se representa el taller de San José, se podrían hacer una idea totalmente equivocada sobre las herramientas utilizadas comúnmente por los carpinteros del siglo XX, porque se harían la idea que ellos no habían a disposición, por ejemplo, herramientas de acero, tornillos, energía eléctrica, iluminación artificial, sierras y taladros eléctricos, colas y barnices obtenidos de sustancias químicas artificiales, recubrimientos de material plástico, etc. Concepto erróneo aún mayor sería pensar que los iconos de las iglesias ortodoxas son representaciones realistas, a partir de que, en el siglo treinta después de Cristo, se pueden hacer suposiciones sobre la vida cotidiana de los que han pintado (hay que recordar que los iconos ortodoxos también hoy en día son pintados tratando de imitar lo más perfectamente posible tanto en los medios como en el estilo los realizados hace muchos siglos; y por lo que podemos entender la religión del Antiguo Egipto fue aún más conservadora que la ortodoxa).

2) Pero volvamos al experimento empírico organizado por Lehner. Dicho experimento debería constituir la prueba definitiva de la correspondencia de la teoría egiptológica oficial con los hechos. Como ya hemos dicho, con el martillo de piedra y el cincel de cobre se ha intentado de hacer una réplica de la famosa “nariz ausente” de la Esfinge, pero realizada en escala 1/3. Obviamente, se inició por el trabajo de desbaste, utilizando los martillos de piedra, como se ve en las imágenes jeroglíficas. La primera dificultad que tuvo que enfrentar es, como por lo demás era de esperar, que con estas herramientas los trabajos avanzaban muy lentamente; por lo que, después de algunos días no se había hecho ningún progreso significativo y la futura nariz seguía siendo indistinguible de una cualquiera piedra tallada. Entre otras cosas, esta prolongación de los tiempos de realización constituía también un grave problema por la salud de los operadores, ya que este tipo de herramientas vibra de una manera muy intensa, de modo que cuando se usan durante mucho tiempo pueden causar accidentes de diversa índole, en particular la severa inflamación de las articulaciones. Esto sucede porque la energía cinética acumulada por la cabeza del martillo, debido a su conformación y el material con el que está construido, no se descarga si no en parte en la trituración de la piedra, pero en gran parte se refleja en un rebote que el mango demasiado delgado no es capaz de reducir de manera satisfactoria y que por lo tanto debe ser absorbida casi en su totalidad de los miembros del operador (pero este detalle durante el documental no se hizo notar). Así, después de un trabajo cansador, no se acumuló si no pocas decenas de gramos de polvo y fragmentos de piedra caliza; y entonces se consideró oportuno no seguir adelante y que lo que se había hecho era lo suficiente y era más que bastante para demonstrar de manera concluyente que los martillos de piedra eran sin duda las herramientas con las que se hizo el trabajo de desbaste de todo el gigantesco monumento (recordamos al lector que la Esfinge tiene unos 50 metros de largo y que su cuerpo se encuentra inmerso en una especie de piscina larga cerca de 70 metros, que tiene el nombre de Recinto de la Esfinge: para conseguirlo tuvieron que extraer varios miles de metros cúbicos de piedra caliza, aunque, al parecer, de mala calidad y por lo tanto bastante tierna). Se creyó así que estaba lograda la prueba deseada y para terminar la operación de desbaste se pasó a las muelas diamantadas, más cómodas y modernas. Lehner no explicó en detalle las razones que le llevaron a esta decisión, pero por el contexto parece de entender que tuvo que abandonar el surco de la precisión histórica no por mala voluntad o para engañar a sí mismo o al público o cosas así. El problema parecía ser otro, a saber que hoy no tenemos a disposición tiempo y mano de obra ilimitados, como era el caso en la antigüedad, y por lo tanto también una nariz en escala 1/3, si se hace con martillos de piedra, costaría una suma de dinero que la venta de documentales y publicidad relacionada no sería capaz de pagar (un día tal vez alguien sin duda nos va a explicar por cual evidencia escrita o de otro género se puede deducir que, por ejemplo, los autores de la Esfinge tenían a disposición tiempo y mano de obra ilimitados; por el momento, la cadena de acontecimientos que parte del orden de un tirano omnipotente para llegar a monumentos de este tipo es una hipótesis sin ninguna base histórica; pero, ya que está en línea con las teorías evolucionistas que se celebran como evidentes incluso antes que verdaderas, ella se aplica a los restos arqueológicos sin preocuparse demasiado si por tal aplicación el significado de esos restos sea iluminado o, en cambio, oscurecido).

3) Después de haber resuelto de esta manera el problema del desbaste, se pasó a las operaciones de acabado. En ellas, con coherencia, a los martillos de piedra se añadieron los cinceles de cobre, estos también copia fiel de los representados en las pinturas y estelas. De hecho, la película mostró que de alguna manera era posible mellar la piedra caliza, pero que al poco rato (como se podía suponer) el cincel de cobre empezó a despuntarse y incluso a doblarse; por lo que muy a menudo había que ponerlo en un brasero de carbón (que se piensa que los antiguos Egipcios no tenían) para forjarlo y ponerlo como nuevo. Esta operación se llevó a cabo con los antiguos martillos de piedra, pero para ser capaz de manejar los cinceles al rojo vivo (colocarlos, girarlos y sacarlos del brasero, revolverlos sobre el yunque) se ha pensado utilizar las tenazas de hierro, aunque la egiptología oficial sostiene que en el tiempo de las Pirámides los Egipcios tenían sólo cobre. Lehner no explicó la razón de esta elección, que contradice sus propias teorías histórico-arqueológicas; y por lo tanto hay que hacerlo en su lugar. El hecho es que, utilizando tenazas de cobre, la operación habría sido bastante difícil, debido a que el cobre transmite el calor con mucha facilidad y las asas habían arriesgado de ponerse al rojo vivo en un corto período de tiempo y así las tenazas serían totalmente inutilizables. Además, cuando el cobre supera una cierta temperatura se deforma con extraordinaria facilidad. Entonces cualquier tipo de tenazas de cobre, usadas intensivamente, tendrían de ser a su vez de nuevo y a menudo forjadas; lo que resulta en una especie de regreso al infinito de tipo práctico, que desde el punto de vista energético es mucho más caro que el de tipo teórico. Incluso antes de empezar su trabajo el herrero encargado de organizar este experimento – era un aficionado de antigüedades, aunque no exactamente un arqueólogo “oficial” – señaló a Lehner que un procedimiento parecido para tallar la Esfinge habría tenido que consumir una cantidad de cobre y madera para avergonzar todas aquellas consumidas en todo el mundo antiguo. Además, nosotros podríamos añadir, se imagine el ambiente infernal en que los pedreros iban a actuar: en Egipto el clima es tórrido durante casi todo el año, y hacer un trabajo físico tan desafiante bajo el sol es una tarea en sí misma agotadora incluso para hombres fuertes y adaptados a las condiciones extremas. Pero se imagine de trabajar en un ambiente donde hay cientos de braseros que queman todo el día y es de suponer no lejos de donde había que empeñarse a fondo en el trabajo durante horas y horas bajo el sol a cuarenta o cincuenta grados, sumergidos por el sudor, el polvo y, si hay un poco de viento, también la arena, la ceniza y el humo que emanaba alrededor. Por supuesto, estamos hablando de cientos de estos hipotéticos braseros, no porque sea razonable pensar que se utilizaron en realidad, sino para tener una idea de lo que significan en la práctica las teorías que se deseaba probar con este experimento. De hecho, al final del documental se ha llegado a la conclusión de que en el trabajo de la Esfinge había 300 pedreros para la duración de 3 años (números que, teniendo en cuenta el tamaño del monumento, ya aparecen a ojo casi ridículamente subdimensionados: si son verdaderos, no se entiende cómo es que monumentos de este tipo no se han hecho en todo el mundo o no se hacen hoy, teniendo en cuenta el enorme progreso técnico que se supone que se ha hecho entretanto). Ahora, estos 300 pedreros tendrían que cambiar a menudo cincel o quedarse quietos: si imaginamos siquiera un solo brasero para cada pedrero ya tenemos 300 braseros con sus asistentes que preparan un cincel aproximadamente cada cinco o diez minutos de intenso uso, de manera que el trabajo pueda seguir adelante sin demasiadas pausas.

4) Cualquiera que haya sido testigo de este experimento (que fue filmado en un documental par National Geographic: “Ancient Secrets: the Sphinx”, que se puede fácilmente encontrar en You Tube) y no sea completamente prevenido, se habría dado cuenta de inmediato de que esculpir una estatua gigantesca como la Esfinge de esta manera es una empresa impensable no sólo por 300, sino también por 300.000 trabajadores aunque motivados y por cualquier período de tiempo: sólo el fuego de los braseros para forjar el cobre requeriría una cantidad de madera para reducir Egipto en un desierto dentro de unos meses. Hay que añadir que la piedra caliza que rodeaba el cuerpo de la Esfinge fue excavada en forma de bloques que llegan a las 400 toneladas y que sirvieron después para construir el templo anexo. A pesar de esto, nadie se ha atrevido ni siquiera a una vaga explicación de cómo tales gigantes han podido ser desplazados incluso de un solo centímetro (¿ rodillas? ¿ trineos? ¿ palancas? Estas son todas cosas que requieren madera, un material ya escaso para los braseros y por lo tanto también para los andamios, los mangos de los martillos, para los barcos de carga, los remos, los muelles, etc.; pero, por otro lado, observamos que en las reconstrucciones en teoría los bloques se mueven con mucha facilidad y en algunas simulaciones computadorizadas incluso parecen casi volar por sí mismos a su lugar; con presuposiciones de este tipo es fácil pensar que los trabajadores del Antiguo Egipto no tenían ninguna dificultad práctica en mover estos pesos enormes, ya que nosotros en teoría no vemos y no queremos ver ningún problema). Cara a esta situación uno se queda desconcertado y incluso incrédulo. Pero así están las cosas: es sólo y exclusivamente en experimentos reales o mentales de este tipo que de hecho se basa cualquier reconstrucción en estilo académico de civilizaciones como la del Antiguo Egipto. A partir de este solo ejemplo (pero hay otros, desde el famoso experimento NOVA, con el que se trató de construir una mini-pirámide de diez metros de altura con los supuestos medios de los constructores de las Pirámides, cuyos resultados fueron desastrosos y por el que Lehner fue acusado de plagio, acusación que parece fundada) se puede entender que la idea del retraso científico-técnico de las culturas prehistóricas no es una “teoría” (porque las teorías tarde o temprano deben confrontarse con la realidad) y ni siquiera una hipótesis que tenga un cualquier sentido heurístico, sino más bien un mero dogma de fe de tipo historiográfico. Pues, nadie debería sorprenderse si este dogma está declarado de manera cada vez más rígida e incondicional gradualmente que nos alejamos de los inventores de la historia, a saber estos Griegos clásicos, de los cuales – por razones no del todo claras – en Occidente seguimos convencidos de que nuestra civilización tiene origen (un día alguien nos va a explicar sin duda lo qué hay en común, por ejemplo, entre la idea de espacio entendido como tensión hacia el infinito expresado por una catedral gótica y la de equilibrio estático expresado por un templo griego clásico). Y poco importa a nuestros historiadores que estos mismos Griegos clásicos, de los cuales se proclaman discípulos y descendientes, afirmen sin ninguna duda que el Antiguo Egipto tenía una cultura mucho más desarrollada que la de ellos. Platón lo dice en serio, pero sus afirmaciones se dan por patrañas: sus famosos diálogos son imbuidos de mitos, fábulas y metáforas, y entonces ¿ cómo se le puede escuchar en un punto tan importante de nuestras reconstrucciones historiográficas?

5) Pero, también Aristóteles – a pesar de la mayor estimación que recoge, entre otras cosas a causa de su alergia al mito – de la parte de nuestros historiadores no obtiene la más pequeña escucha cuando, con intención que parece sarcástica, dice que los sacerdotes egipcios utilizaban las matemáticas para diversión. (Como es bien conocido, en la visión de Aristóteles la ciencia verdadera no tiene nada que ver con las matemáticas; y, por lo demás, no hay huellas de matemáticas tampoco en los llamados “físicos” griegos; de hecho, el método de la física occidental, por lo menos desde Galileo, se ha desarrollado en oposición directa a la τεορία de los filósofos griegos, incluyendo los atomistas; pero esta constatación y otras similares no desalientan a los partidarios de la ascendencia griega de nuestra ciencia cuantitativa y nuestras matemáticas; se trata de clichés históricos no mucho más fundados que el retraso tecnológico del hombre del Neolítico). Pero, sin hablar de Platón y Aristóteles, hay bastante otros hombres de cultura antiguos que dicen que los Griegos clásicos han importado su cultura astronómica y matemática de Egipto (o incluso desde Babilonia de la edad tardía). Sin embargo, en nuestras universidades sin inmutarse siguen sosteniendo que las matemáticas y la astronomía matematizada son creaciones de los Griegos clásicos y que en el Antiguo Egipto no se sabía nada de eso hasta la llegada de Alejandro Magno. Sin embargo, el número de oro y el P griego salen por todas partes en las medidas características de la Gran Pirámide hasta el punto que unos influyentes profesores de matemáticas y estadística excluyen que se trate de un caso. De hecho, se ha constatado que en Nabta Playa hay alineaciones megalíticas que demuestran que los constructores del círculo conocían la distancia relativa entre la tierra y algunas de las estrellas de Orión. Esto a su vez es la prueba de que en 7000 a. C. ya se tenía una idea clara de que era una estrella y de la conformación efectiva del cosmos, ya que el conocimiento de algo como la distancia relativa de las varias estrellas de una misma constelación en sí misma excluye que se pueda pensar en el universo en términos de una rígida sucesión de esferas. Sin embargo, estos y otros datos objetivamente verificables no sirven para causar la más mínima duda entre los arqueólogos académicos: no importa lo que se diga, ni siquiera pensar que en el Antiguo Egipto había algo ni remotamente parecido a matemáticas o astronomía matematizada mínimamente desarrolladas, y aún menos una ciencia exacta o una técnica que derive de ella.

TERCERA PARTE: HUELLAS DE UNA CIENCIA ANTES DE LA CIENCIA EN LAS MEDIDAS DE LA GRAN PIRÁMIDE Y OTRAS MANUFACTURAS DEL ANTIGUO EGIPTO

1) Pues los que hemos expuestos son los métodos y concepciones que en el ámbito de nuestra historiografía y arqueología oficiales se adoptan como herramientas indiscutibles de conocimiento de todo nuestro pasado prehistórico (y, por lo tanto, no sólo de los antiguos Egipcios). Pero, como el lector ya habrá adivinado, es totalmente obvio que estos métodos y estas concepciones no son de ninguna manera los únicos posibles y, en particular, el enfoque que le hemos dado a este trabajo no tiene nada que ver con los métodos y las concepciones con que los profesores y intelectuales que pertenecen a los diversos campos del conocimiento reconstruyen por vía dogmática el pasado de la humanidad. Así que desde el principio hemos renunciado a las interpretaciones habituales del estilo académico y también a la interpretación de los fenómenos geométricos examinados usando por enésima vez el caso, esa extraña divinidad moderna que aparece dondequiera como Polichinela (con esto queremos decir que ninguno de los proponentes de este extraño tipo de creencia religiosa se atreve a dar un solo paso para definir lo que realmente constituye este caso omnipotente, que lo crea todo y lo destruye todo, cómo se forma o si se forma un campo de probabilidades donde puede actuar, cómo este campo de probabilidades se puede definir y describir, si matemáticamente o de otra manera, de cuáles fuerzas se sirva y cómo, etc.). Por lo tanto, la elección hermenéutica que nos guiará durante toda la argumentación que vamos a desarrollar en este artículo, es la que nos aparecía la más espontánea, la más intuitiva y, sobre todo, la más sostenible matemáticamente. A saber, que realmente los constructores de las Pirámides estaban en posesión de los puntos más avanzados que actualmente están conseguidos por la ciencia empírica occidental y que la Gran Pirámide fue diseñada como la proyección en código de este conocimiento. Por supuesto, nos damos cuenta de que no sólo a los historiadores y arqueólogos académicos, sino también a muchos intelectuales de otros campos y por lo tanto de otras academias la idea de conectar la más famosa teoría de Einstein con el arte sagrado del Antiguo Egipto parecerá sin duda lo más absurdo, una fantasía más adecuada para una película de ciencia ficción que para la comprensión del significado de monumentos como la Gran Pirámide o de representaciones de estilo “poco realista” o incluso “un poco infantil” como el que se supone típico del arte figurativo del Antiguo Egipto. Esto sucede porque en el ámbito de toda la cultura oficial de nuestros tiempos se cree de forma totalmente acrítica y apriorística que estas obras maestras del arte y la arquitectura sagrados han sido creadas en tiempos prehistóricos o casi prehistóricos por hombres que todavía tenían un pie en el Neolítico, a saber y hablando claramente, por semisalvajes. Pero vale la pena repetirlo: estas ideas no son el resultado de un profundo análisis crítico y científico de los restos arqueológicos que tenemos. Es más bien un sistema a priori de molde ideológico, que con el tiempo se ha convertido en una especie de idea fija de la cultura académica occidental: pueblos como los antiguos Egipcios, ya que estaban justo fuera de la Edad de la piedra, tenían que estar más cerca del estado animal y por lo tanto menos inteligentes y “avanzados” que nosotros. Por ello, no hay necesitad de perder el tiempo preguntándose si por casualidad pueden tener un significado científico y matemático que tal vez nos ha escapado hasta ahora.

2) Pero, como ya hemos visto y demostrado al menos en parte, estas sugerencias no nos llegan en absoluto de la ciencia empírico-matemática ni siquiera de la historia y la arqueología en el sentido propio. Si dejamos de lado nuestros prejudicios culturales y vamos a ver lo que la historia, la arqueología y, sobre todo, las ciencias empírico-matemáticas nos dicen acerca de muchas culturas de la Edad de la piedra – por lo tanto de la cultura de los antiguos Egipcios, pero también de los constructores de obras como las que se pueden ver en Baalbek, Ollantaytambo, Puma Punku, Sacsaywaman, Alatri, Delfos, etc. – es que estas personas tenían a su disposición una técnica y pues una ciencia de las que derivaban una capacidad de procesamiento de la piedra que para nosotros es absolutamente inconcebible. La construcción de cientos de metros o incluso kilómetros de muros poligonales (en Alatri los kilómetros son más que cuatro) con piedras a doce, catorce o más lados, con un peso hasta las 400-600 toneladas, con encajes que aparecen de tolerancia inferior al milésimo o incluso diezmilésimo de milímetro, es para nosotros una empresa absolutamente única: viendo un aterrizaje de extraterrestres mucho menos deberíamos sorprendernos que cara a los rompecabezas de piedra que la prehistoria nos ha dejado en herencia. Decimos esto porque, dados nuestros conocimientos técnicos y científicos, los viajes espaciales también muy difíciles sin embargo son para nosotros pensables y en parte también realizables; si todavía no hemos conquistado un planeta como Marte, esto no sucedió sólo a causa de las dificultades de la empresa, sino también porque se han perdido la mayor parte de las motivaciones culturales y ideales que han sostenido el tremendo esfuerzo que non llevó a la luna. Por lo contrario, los encajes de piedra de cierto tipo son completamente más allá – no decimos de nuestras posibilidades prácticas – sino también sólo de nuestra capacidad de hipótesis técnico-científica. Pues, que el hombre de la Edad de la piedra todavía estaba cerca de la etapa animal, que tenía una organización social aproximada, que no tenía un lenguaje escrito ni conocía las matemáticas, la astronomía ni siquiera herramientas banales como la rueda o la polea, no es el análisis científico-crítico de los restos arqueológicos a nos decirlo, sino una particular interpretación de la historia que se suele llamar “evolucionismo”, que en el estado actual de los conocimientos parece basarse en el mismo tipo de fundamento en que se basa un castillo de papel. Lejos de tener algo que ver con el método científico o con un método empírico de cualquier tipo, esta extraña clase de fe, al mismo tiempo seudo-religiosa y seudo-científica, nos empuja a repetir y transmitir servilmente un sistema de prejuicios totalmente infundados y, en particular, el que nuestro pasado prehistórico había sido un sinfín de edades de animalidad y barbarie. Y todo eso sin que nadie o casi nadie se preocupe en controlar si proposiciones de este tipo tienen realmente algo que ver – no decimos con la realidad que en sentido amplio se puede definir perceptible – sino tan sólo con la realidad mensurable y por lo tanto científicamente controlable. De hecho, hemos visto como algunos restos arqueológicos, si son tomados en serio, muestran signos evidentes de una cultura matemática, geométrica y astronómica de un nivel muy alto (basta pensar en la obra de Tom Brophy sobre el Círculo megalítico de Nabta Playa), por no hablar de las técnicas de procesamiento aplicadas a la piedra que, como ya decimos, requieren herramientas que en Occidente todavía tenemos que reinventar (asumiendo que vamos a ser capaces de hacerlo: desde los tiempos en que Petrie dijo esta frase no es que las cosas han cambiado mucho). Es cierto que en el mismo período a que se atribuyen restos que atestiguan la existencia de culturas muy avanzadas la arqueología ha descubierto otros que hablan de culturas más bien primitivas. Pero ¿ qué puede significar en realidad esto en cuanto al estado de una civilización como la de Tiahuanaco y Puma Punku, que la arqueoastronomía coloca más o menos en 15.000 años antes de Cristo? Allí nos encontramos con restos de construcciones que parecen realmente obra de divinidades y no de seres humanos: ¿ tenemos que negar lo que vemos sólo porque en el mismo período encontramos otro tipo de restos, que en cambio nos inclinamos a atribuir a pueblos tecnológicamente atrasados? Para nosotros, que vivimos inmersos en nuestras ciudades, en medio de coches y teléfonos móviles, es totalmente espontáneo olvidar que Einstein fue contemporáneo no sólo de personas como Bohr, Heisenberg, Wittgenstein, Picasso y similares, sino también de todas aquellas personas que incluso al comienzo de 1900 no habían conocido la civilización. ¿ Qué diríamos si entre quince o veinte mil años una civilización desarrollada pero completamente diferente de la nuestra negara la posibilidad que en 2000 d. C. podría haber existido una civilización avanzada, porque sus restos coexisten con los de los aborígenes australianos? Es muy fácil sostener con sorna que la atribución de cualquier versión de la teoría de la relatividad al Antiguo Egipto es una locura digna de un película de Hollywood. Sin embargo, será menos fácil la explicación de todas aquellas cosas que vamos a ver en las páginas siguientes, que, por extraño que puede aparecer, serán aún más impresionantes que las que hemos visto en las primeras.

3) Antes de entrar en los detalles de nuestra investigación, es bueno recordar de nuevo que hasta hoy las matemáticas y la astronomía del Antiguo Egipto han sido consideradas al nivel de los niños de la escuela primaria o poco más. Esto ha significado que – al menos en el ámbito de la egiptología oficial – cuando se oía decir que Newton quería conocer las dimensiones exactas de la Gran Pirámide con el fin de calcular las de la tierra, la reacción más benévola podía ser una sonrisa de compasión. El impulso de sonreír tal vez tendrá a disminuir cuando se analice con un mínimo de seriedad imágenes como las que hemos mostrado en la primera parte de este trabajo y a lo mejor irá por completo una vez que nos dimos cuenta de que todas o casi todas las constantes de nuestras leyes científicas se pueden derivar con muy buena aproximación de simples funciones de π y ϕ, o sea justamente de los dos números que de muchas maneras caracterizan las relaciones entre las medidas de la Gran Pirámide. Por lo tanto, la presencia de estos números en el monumento puede significar algo mucho más profundo que el conocimiento de algunos conceptos básicos de la geometría euclidiana. Es verdad que π ya tiene un papel importante en la estructura de los distintos tipos de dinámica que se han desarrollado en Occidente en los últimos siglos. Pero ¿ cuál podría llegar a ser su papel teórico cuando se descubra que las variables presentes en nuestras fórmulas más utilizadas pueden ser pensadas como funciones de π y φ? Para dar al lector una primera y muy breve muestra de lo que podría significar el conocimiento de estos números en relación a la estructura profunda de las ciencias exactas, empezamos justamente por la ley de Newton. Si aplicamos la fórmula (π x ϕ) + π/2 el resultado es un valor de 6,65399, que es muy cercano al valor que atribuimos a la constante G, que es 6,67428. Pero – sobre todo después de que nos dimos cuenta de las íntimas conexiones entre el espacio sagrado del Antiguo Egipto y la teoría gravitacional de Einstein – podríamos o incluso deberíamos reemplazar en esta fórmula los valores de π y ϕ, así como resultan de la demonstración geométrica, con los que en cambio encontramos como valores aproximados en la Gran Pirámide (recordemos que en este monumento π es la mitad del perímetro dividido por la altura, π/2 del lado dividido por la altura, y ϕ del área de la base dividida por la de las cuatro caras triangulares). Por lo tanto, podríamos sustituir π y ϕ con las relaciones entre los valores de las medidas de la Gran Pirámide, alcanzando de esta manera la fórmula que calcule la constante gravitacional (o tal vez, de manera más complicada, podríamos partir de la constante gravitacional para llegar a las medidas de la Gran Pirámide). De todas maneras, por amor de brevedad y sencillez, la escribimos con los valores a los que hemos llegado por medio de levantamientos metrológicos. De este modo se llega a un resultado equivalente a πKeops x ϕKeops + πKeops/2 = (3,142857 x 1,61859) + 1,5714285 = 6,6584. El valor de la constante es G = 6,67428, con una diferencia de 6,67428 – 6,6584 = 0,01588. Recordemos que el valor de la constante oscila de ± 0,0067. Por lo tanto, la diferencia entre el valor mínimo que se puede utilizar en la fórmula de Newton y el que obtuvimos de πKeops y de ϕKeops es aproximadamente 0,00918, es decir un poco más de 9 milésimos. Cabe señalar, sin embargo, que los aproximadamente 15 milésimos de diferencia iniciales se podrían prácticamente poner a cero alargando un poco la fórmula y escribiendo πKeops x ϕKeops + πKeops/2 + (1 – 1/ϕKeops)10 (cuyo valor corresponde en números a 0,001326): la diferencia se reduciría a un par de diezmilésimos.

4) Pero, en lugar de estos valores que derivan de las medidas de la Gran Pirámide podríamos dejar ϕ así como resulta del cálculo geométrico y, por lo que se refiere a π, utilizar un valor de los que se pueden sacar de otros artefactos del Antiguo Egipto. Por ejemplo, podríamos tomar el que, por lo que parece, se utilizó para construir el sarcófago de Djedefre, cuyas medidas parecen rodear entorno a un número tanto enigmático cuanto aparentemente insignificante: el 234. Sin embargo, si tenemos en cuenta un ciclo estelar importante para los antiguos Egipcios, el de Sirio, y vamos a dividir su número típico, el 1461 (correspondiente a los años de su duración) por este misterioso 234, y luego dividimos otra vez el producto por 2, vemos que sale un número muy cercano a π, a saber 3,1217, que difiere de π de menos de dos centésimos. Por lo tanto, parece bastante claro que también en este caso los antiguos Egipcios han querido incluir en el sarcófago del Faraón un número que de manera hermética se relacionara por un lado con Isis – la divinidad de la cual la estrella Sirio tal vez era el símbolo más importante – y por otro lado con la constante geométrica característica del círculo, y por lo tanto también de los ciclos cósmicos, concebidos simbólicamente como círculos. Si para calcular la constante gravitacional utilizamos este valor de π, con esta otra fórmula (πDjedefre x ϕ) + ϕ tenemos que (3,1217 x ϕ) + ϕ = 6,66905, con una diferencia con respecto a nuestro valor de G incluso más irrelevante (-0,00523), que además también cae dentro del margen de oscilación de nuestra constante. Si aún, así sólo por mera curiosidad especulativa, comprobamos lo que sucede aplicando este tipo de método a la constante de Planck, nuestro asombro se renueva, ya que en este caso con fórmulas basadas en π y ϕ conseguimos resultados aproximados mejores. Si tenemos en cuenta el 6.55 por 10⁻²⁷ ergios por segundo utilizando la fórmula (π²/2) + ϕ encontramos un 6,5528, es decir una cifra que se aproxima mucho al valor de la constante (+ 0,0028). Un resultado similar, aunque no tan bien aproximado, sale de manera aún más fácil multiplicando el número de oro por cuatro, ya que ϕ x 4 = 1,618033 x 4 = 6,472132. Las cosas no cambian mucho si consideramos el valor de la misma constante calculado en julios, que es de 6,62559 x 10⁻³⁴ julios por segundo. Si en este caso tratamos de aplicar la fórmula (π x ϕ) + π/2 – [1 – √(√(√(√(√ϕ)] llegamos a un valor de 6,6234, con una diferencia de menos de 3 milésimos. Pero la constante de Planck (símbolo “h”) a menudo es substituida por otra constante – desarrollada por Dirac – que se llama “hache cortada” (símbolo “ħ”), que tiene un valor igual a 1,054571. Podemos conseguirla con un valor aproximado de alrededor de un milésimo con la fórmula 1 + (1 -1/ϕ)3 = 1,055728 o ⁹√ɸ = 1,054923213178.

5) Nos damos cuenta de que un procedimiento de este tipo puede parecer en un principio totalmente arbitrario y carente de cualquier fundamento empírico. Por otro lado, también nos puede mostrar que las constantes más importantes de nuestra física podrían tener algo en común entre sí o que, de todos modos, para hombres que tienen una visión espiritual diferente de la nuestra podrían no parecer esos números casuales y sin ulterior aplicación como parecen a nosotros. De hecho con π y ϕ nos podemos acercar también a la constante donde se saca la velocidad de la luz, que es 2,9979246. Aplicando la fórmula πKeops – (1/ϕ)4 llegamos a 3,142857 – 0,145898 = 2,996959, que se desvía del número correcto de un poco menos de un milésimo (para ser precisos: 0,000961): añadiendo a este número, por ejemplo, el valor que sale de (⁵⁰⁰√ϕ – 1 = 0,000962) llegamos a 2,997921, que es realmente muy cercano al valor de nuestra constante. Ahora bien, si a esto añadimos que la velocidad de la luz ha sido magistralmente codificada en la base de la Gran Pirámide, hay que preguntarse: ¿ es realmente una apuesta hermenéutica sin fundamento, o incluso un delirio de fantasía histórica, asumir que el diagrama del espacio-tiempo fundado en π y ϕ, que también está ahí codificado, no está ahí por una broma del destino? Piénsese en esto: después que en el espacio sagrado del Antiguo Egipto ha sido detectado un conjunto no cuestionable de características geométricas y metrológicas que, por lo que sabemos, sólo pueden derivar del conocimiento de la teoría de la relatividad, ¿ no es cosa más racional y científica afirmar que los antiguos Egipcios conocían esta teoría (aunque en una versión diferente de la nuestra) que explicarlo todo con el llamado “caso”, que no es otro que el nombre con el que hemos bautizado nuestros prejuicios, nuestro cansancio, nuestra renuncia a cuestionar nuestras cómodas y apriorísticas certezas en favor de una explicación tal vez intelectualmente muy incómoda, pero creíble y auténtica? Hay momentos en que se pierde la esperanza, pero tal vez un día también en las instituciones de la arqueología oficial alguien va a despertarse y darse cuenta de que explicar cualquier rasgo de excepcionalidad que encontramos en la técnica o en el conocimiento matemático y científico de nuestros antepasados con el caso no es que el fruto más venenoso de una pereza espiritual que daña nuestra inteligencia y nuestra perspicacia, la máscara del miedo disfrazado de arrogancia, que es un empobrecimiento general de nuestra identidad y de nuestra herencia histórica y científica. Shakespeare, tal vez el más grande poeta del Occidente moderno, hizo decir a su héroe una expresión que se ha convertido en el símbolo de la apertura del asombro humano a lo ignoto que trastorna el saber que se creía establecido y indiscutible: “Hay más cosas entre el cielo y la tierra, Horacio, que las soñadas en nuestra filosofía”. Es lo que dice Hamlet, que, hablando con un amigo de la universidad, alude al fantasma de su padre regresado del Purgatorio a pedir venganza. Pero podría ser que esta frase también se adapte a nuestro caso, que las imágenes que vimos en la primera parte de este artículo sean el fantasma de una era de la humanidad que emerge del pasado para pedir justicia a nuestra historiografía evolucionista, que de manera totalmente infundada afirma que nunca ha existido. De hecho: ¿ qué sabemos de las formas que pueden tomar las matemáticas y la ciencia matematizada en culturas diferentes de la nuestra para descartar a priori que puedan haber sido utilizadas incluso como arquetipo de figuras y monumentos sagrados? Tal vez a menudo nos olvidamos, pero uno de los monumentos más famosos de la modernidad, la Tour Eiffel, no es más que la expresión arquitectónica de una función matemática que tiende al infinito, es decir la explicación clara y consciente de lo que podemos considerar como el significado escondido de las catedrales góticas. Y ¿ no se ha dicho lo mismo, y con razón, incluso de la música barroca – una especie de catedral de notas que se adentra en un infinito simbolizado por el silencio – que no sería que matemáticas para escuchar? Por supuesto, nos asombra a ver a gente que se le atribuye la teoría de la relatividad andar con extrañas faldas cortas y con sombreros que hoy en día, incluso en los desfiles de moda más provocativos y transgresivos, serían considerados – cómo decir – un poco excesivos. Un físico serio, desde el nuestro punto de vista, tiene que ir para ahí con traje y corbata, de lo contrario demuestra inequívocamente que es un idiota, tal vez un salvaje. Por otro lado, Freyman fue un frecuentador habitual de los campos nudistas, pero esto no le impidió el logro de los resultados que la comunidad científica ha reconocido como sin duda interesantes.

6) Pero, más allá de cualquier juicio de tipo exterior o estético, a una mente educada por la modernidad esta manera de calcular o, como tal vez se debería decir, de decidir a priori que los valores de las constantes pueden o deben ser derivados de π y ϕ (y que, por lo tanto, las leyes científicas sean en última instancia funciones de estos mismos valores) aparece como un sistema de forzamientos, con los cuales – pasando por alto la realidad experimental – se quiere a toda costa conectar las leyes científicas en un sistema unitario, que la investigación no parece justificar. Si un investigador moderno quería obtener los números fundamentales de las leyes científicas por ciertos valores mantenidos como sagrados o incluso adorados como dioses (porque justamente esto parece indicar el hecho que π y ϕ se codificaron de modo sistemático en el arte sagrado del Antiguo Egipto; es bueno también recordar que en aquella cultura como por lo demás en otras culturas antiguas no se encuentra traza de un arte que se pueda definir como profano) tal vez la comunidad científica podría responder diciendo que esta persona aún no ha entendido lo que es el modo de proceder de un verdadero científico, cuyo trabajo consiste en olvidarse de cualquier tipo de ideologías apriorísticas y en someter su trabajo intelectual y matemático a la realidad empírica detectada operativamente. Esta forma de pensar está tan arraigada en nosotros que es difícil de explicar a cualquier persona, incluso a veces a los científicos, que podemos pensar en tales cosas sólo desde la remoción del proceso histórico concreto que llevó al descubrimiento de las teorías científicas hoy en boga. Sólo a partir de esta remoción se puede creer tanto firmemente cuanto acríticamente que nuestras teorías no son nada, por así decirlo, que un zumo de hechos, y por lo tanto que están constantemente en contacto directo con la realidad empírica. A menudo – aunque no siempre – nos olvidamos de que a principios del siglo la física teórica era mucho más importante que la experimental y que los experimentos reales fueron casi siempre diseñados y producidos como proyección de experimentos mentales, en los cuales objetos ideales eran manipulados por medio de signos matemáticos (esto ha ocurrido sobre todo en el caso de la mecánica cuántica: basta pensar en los aparatos construidos específicamente para poner a prueba la famosa “discrepancia de Bell”). O, para poner un ejemplo más famoso, durante los años ’20 la mecánica de las matrices desarrollada por Heisenberg fue rápidamente reemplazada por la función de onda de Schrödinger no porque era “más exacta”, sino simplemente porque por un lado era mucho más conveniente para el cálculo y por otro porque permitía conservar al menos en parte esa imagen de los fenómenos electromagnéticos que se tenía en la física clásica desde los experimentos de Young sobre la interferencia de las ondas luminosas (más tarde Dirac descubrí que tanto la mecánica de las matrices como la función de onda se pueden derivar de una teoría aún más abstracta). Pero ¿ podemos estar totalmente seguros que la mecánica cuántica sería hoy la misma si la función de onda no se hubiera inventada y los físicos y matemáticos en el siglo siguiente hubieran trabajado para refinar la física de las partículas a través de la imagen matemática de las matrices? ¿ con qué expresión y con qué consecuencias filosóficas habríamos sustituido la definición actual de una partícula como una “onda de probabilidades”? ¿ estamos seguros de que el pensamiento humano, si es guiado por diferentes símbolos, no pueda llegar a diferentes resultados, incluso investigando el mismo campo de fenómenos? De hecho, incluso fuera del llamado “mundo de las partículas” – donde parecen estar en vigor leyes que no tienen nada que ver con el mundo cotidiano – para entender los fenómenos perceptibles por los sentidos, como el movimiento de los cuerpos macroscópicos, estamos acostumbrados a utilizar imágenes matemáticas de cuerpos que se encuentran en condiciones ideales: todos sabemos que el movimiento rectilíneo uniforme es el que caracteriza un cuerpo que se mueve sin encontrar roce, es decir un cuerpo que no existe. Sin embargo, es precisamente esta imagen de un cuerpo que no existe que hace comprender todas estas teorías que describen lo que ocurre con los cuerpos que existen, los que en cualquier momento tocamos con nuestras manos y vemos con nuestros ojos. ¿qué pasaría entonces si se habituara a un niño a la creencia de que los cuerpos tienen tendencia a permanecer inmóviles hasta que – por así decirlo – una divinidad no decida de moverlos? ¿ cómo reaccionaría a la enseñanza de una física que ya por su nombre (“dinámica”) supone que la palabra “mundo”, la palabra “conocimiento” y la palabra “movimiento” de alguna manera son sinónimos? A una mirada más cercana, vemos que no existen y tal vez ni siquiera son posibles comprensiones “neutrales” de la ciencia, independientes de imágenes que nos dan la posibilidad de representarnos el significado de las ecuaciones de forma sintética. Quien conoce un poco más a fondo la ciencia moderna y su historia es perfectamente consciente de cómo durante décadas los físicos se han dividido de manera similar a lo que se hace en política entre “revolucionarios” y “reaccionarios”. Los primeros eran los defensores de la interpretación de la mecánica cuántica llamada “de Copenaghen”, que renunciaban a los principios de identidad y causa en favor de los de complementariedad y incertidumbre; los segundos, seguidores de Einstein, fueron los que pensaban que esta interpretación de las ecuaciones debía considerarse incompleta y que, bajo el “revolucionario” indeterminismo del mundo microscópico, se escondía el “viejo” determinismo del mundo macroscópico. Pero ¿ este extraño tipo de enfrentamiento entre conservación y revolución en el ámbito de la física matematizada no es la prueba indubitable que se puede estar a favor de una determinada interpretación de los resultados de la ciencia siguiendo tendencias culturales y psicológicas que tienen poco que ver con hechos y experimentos?

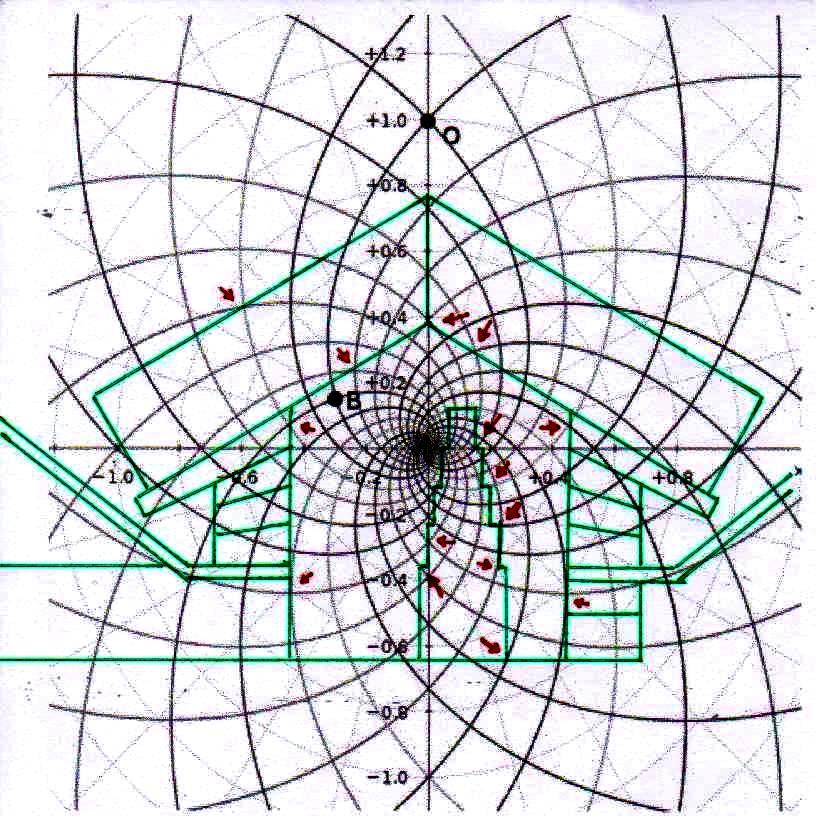
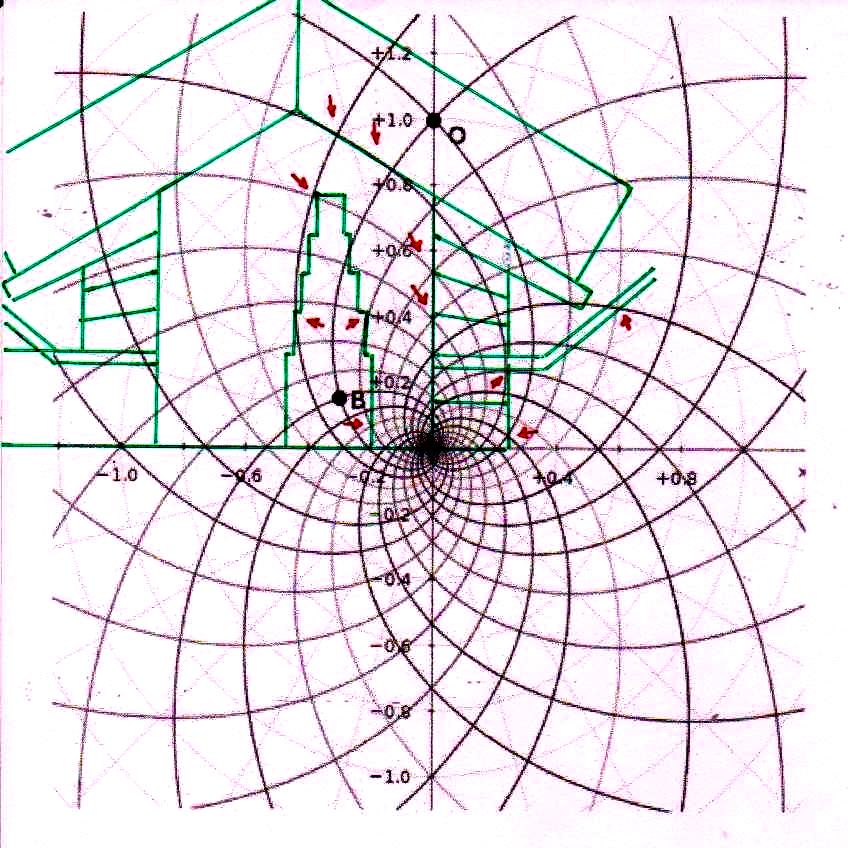
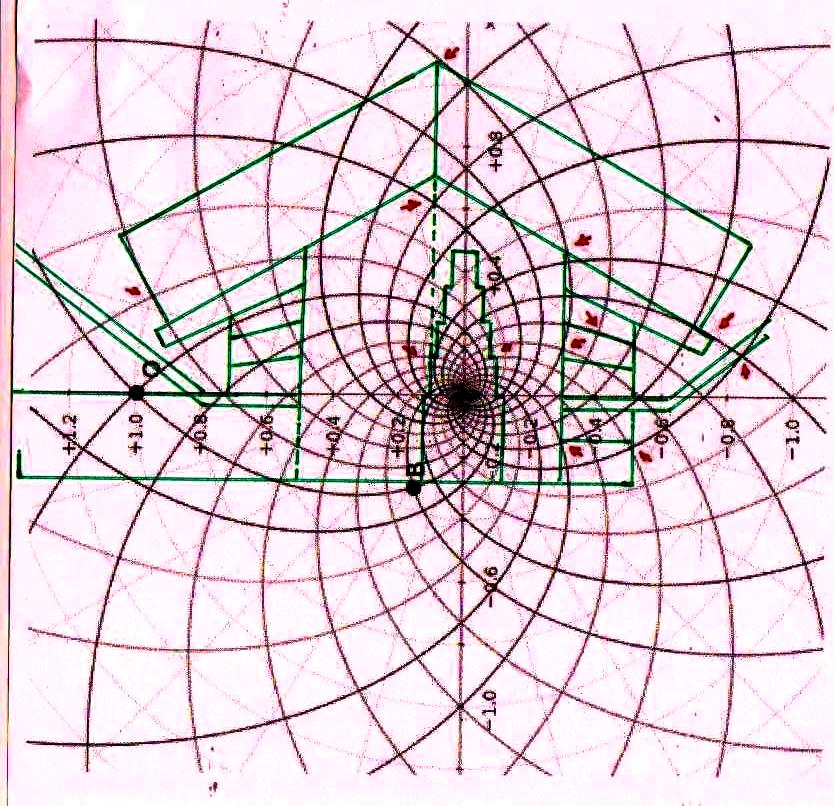
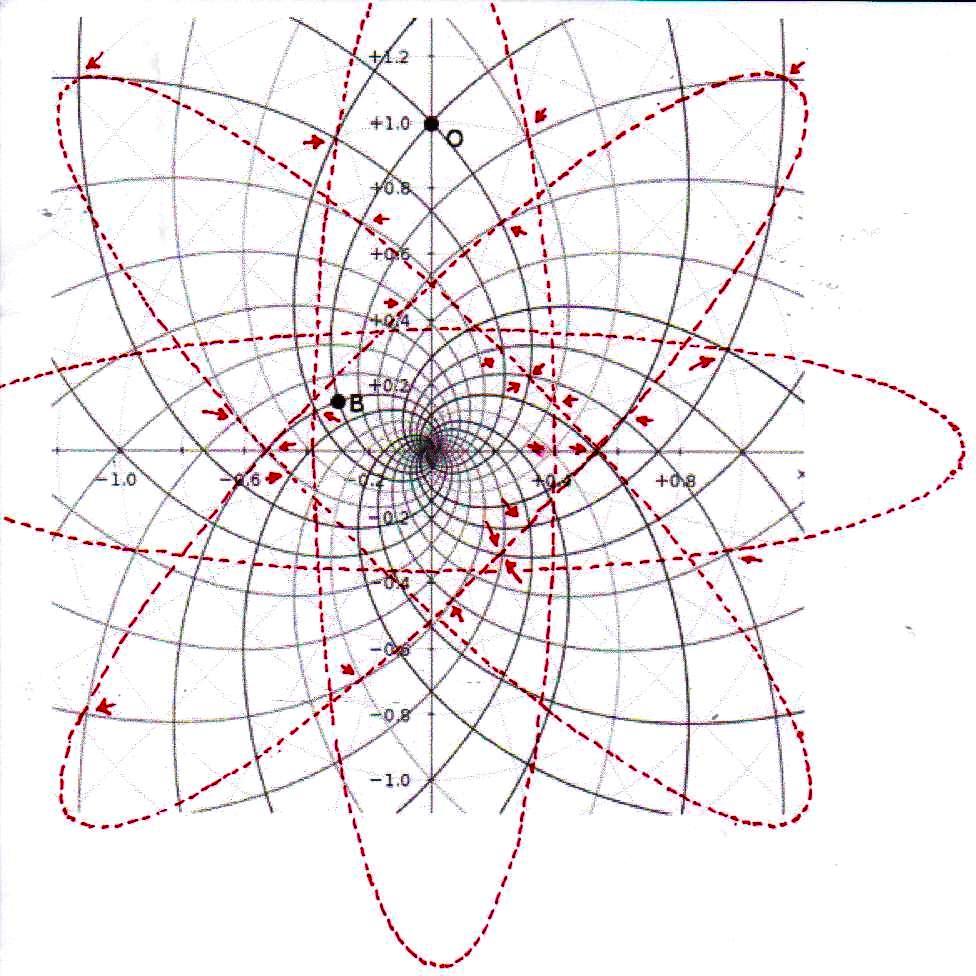
7) De hecho, si hemos asistido a toda esta “polémica política” en el ámbito de la física microscópica sin perder confianza en su objetividad y eficacia, ¿ por qué no debería haber existido una cultura donde – por ejemplo – las constantes se derivaban todas de π y ϕ, entendidos como números divinos ideales, para después llegar a los reales por medio de procedimientos de alguna manera relacionados con los que nos permiten de calcular el movimiento de un cuerpo real a partir de la imagen matemática de un cuerpo ideal? En la primera parte de este artículo hemos visto cómo el espacio-tiempo puede ser proyectado geométricamente sobre un diagrama bidimensional constituido por un sistema de círculos y espirales logarítmicas o, en última análisis, de funciones de π y de ϕ. Tal vez sea útil volver a verlo en la imagen de abajo así como de hecho aparece, sin que las imágenes a las que se ha superpuesto perturben su comprensión

 

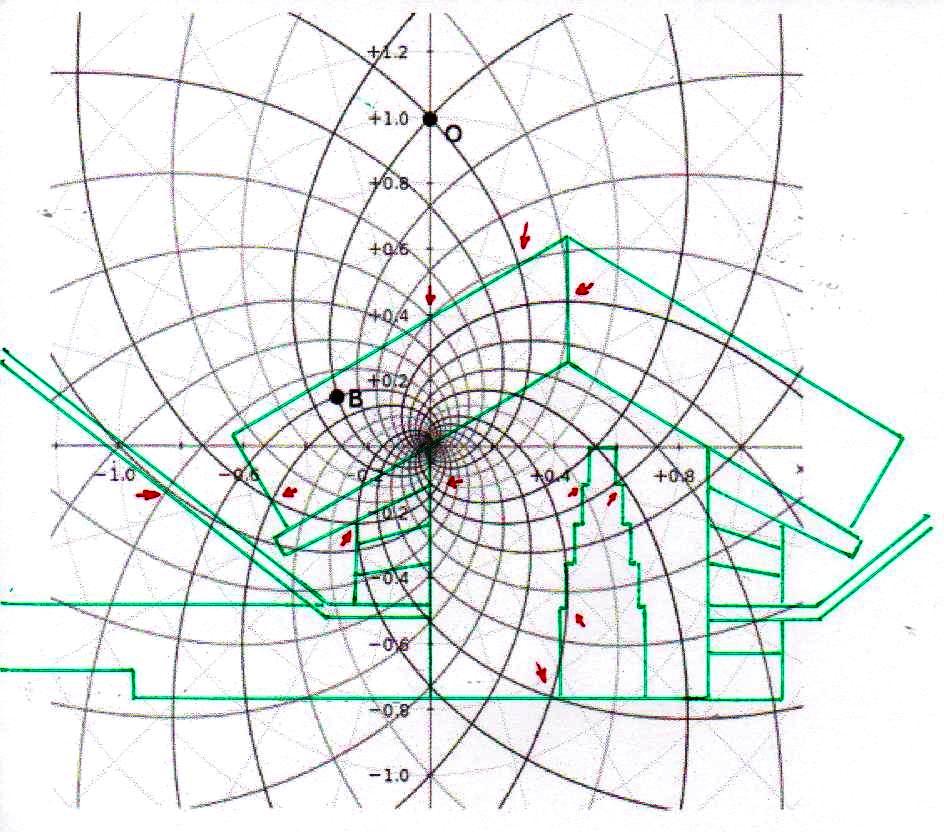
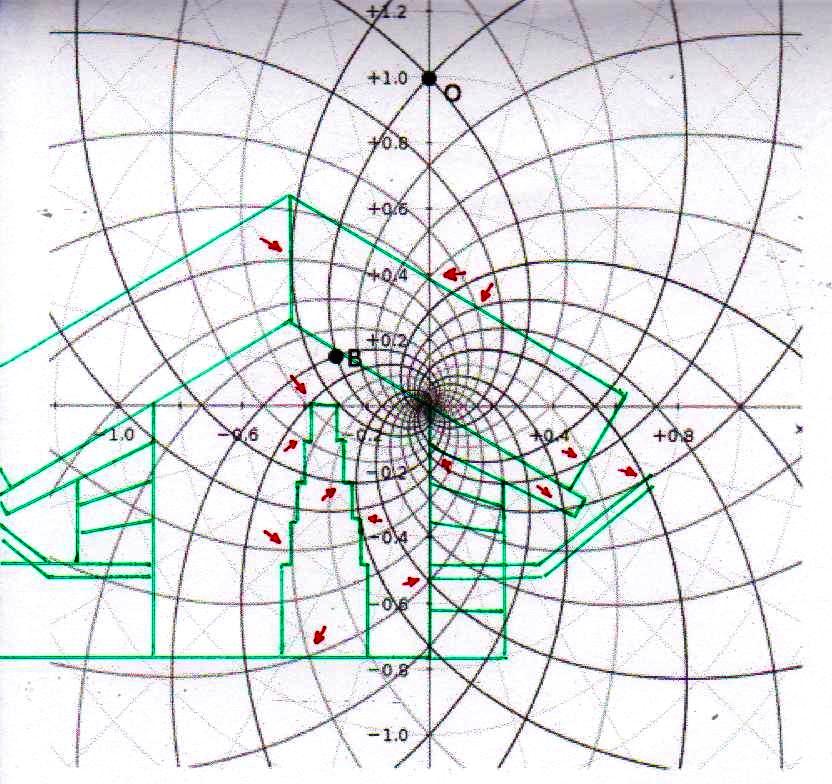
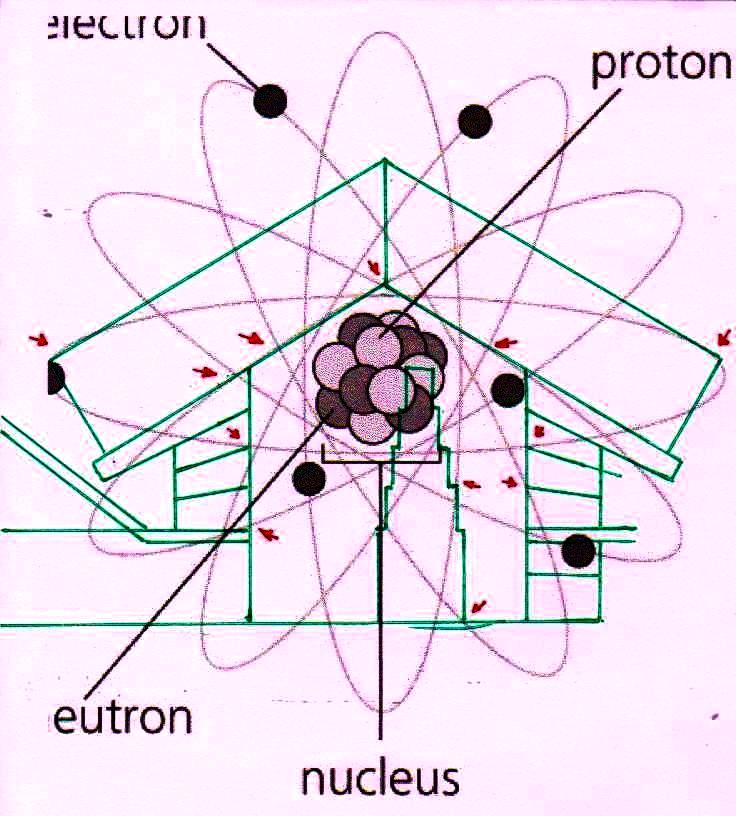
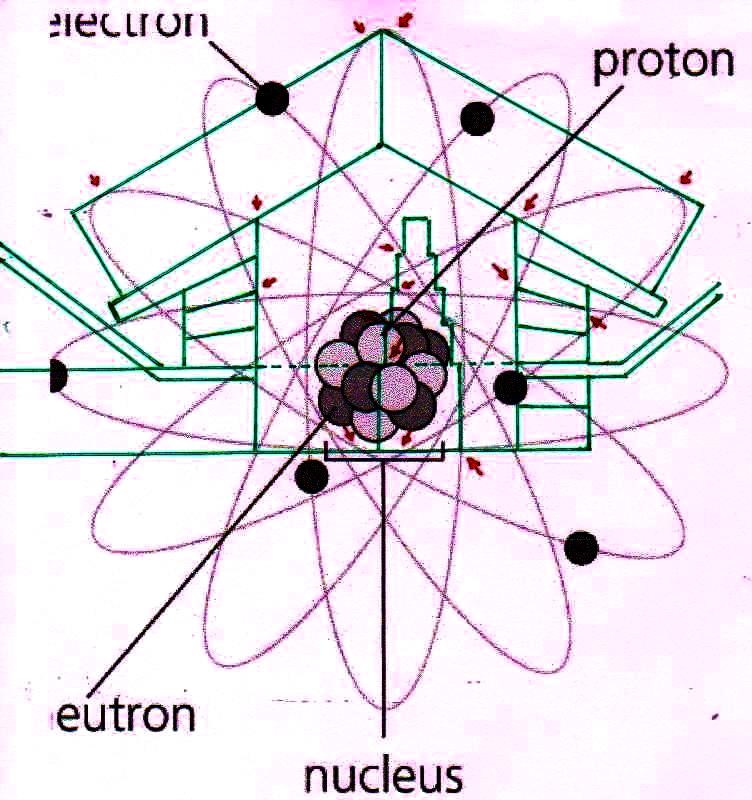
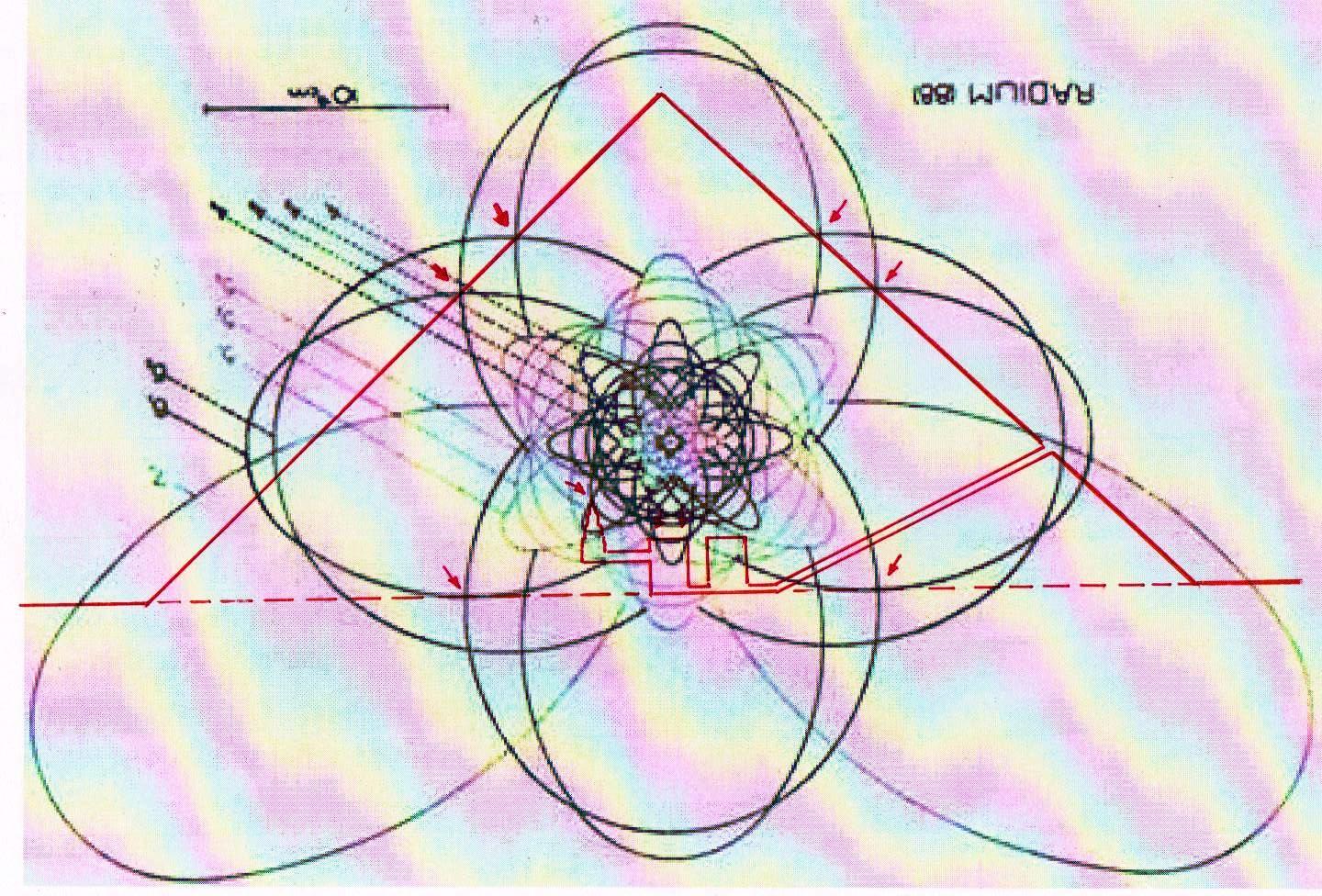
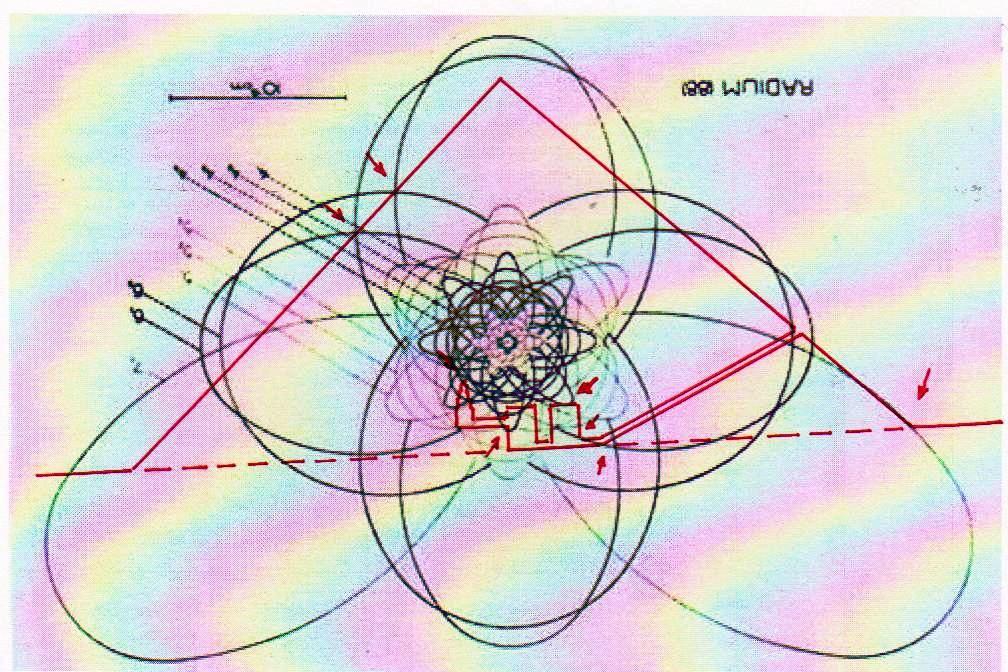
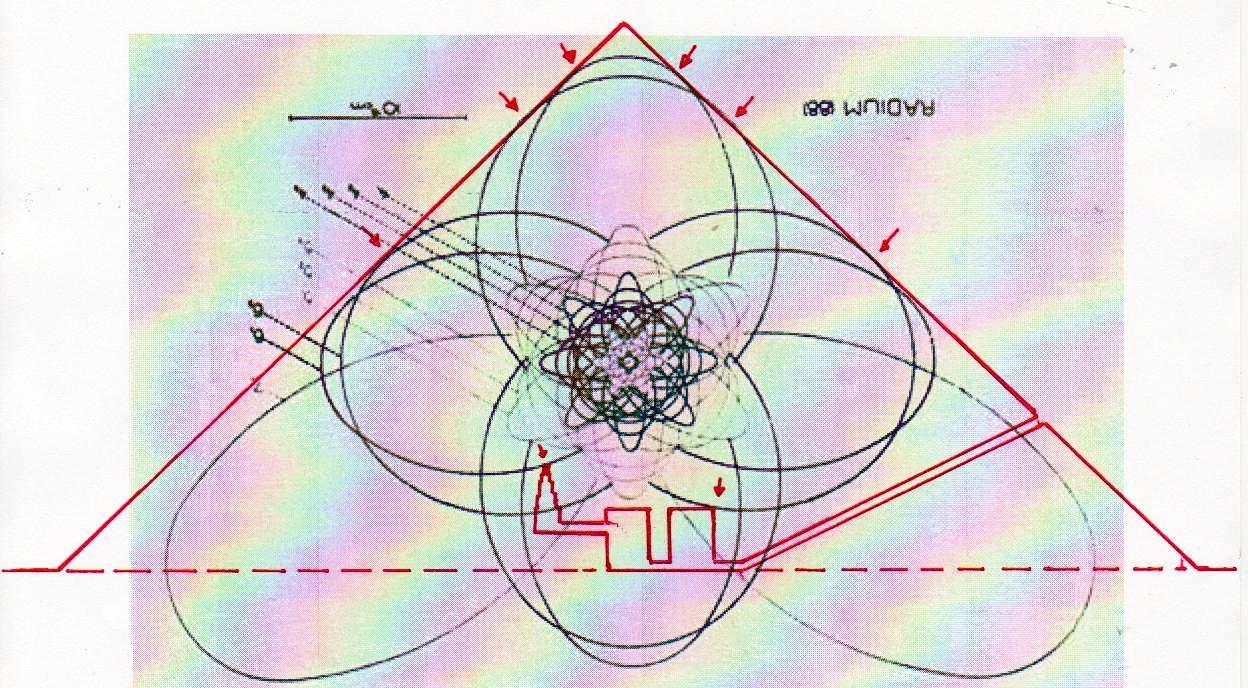
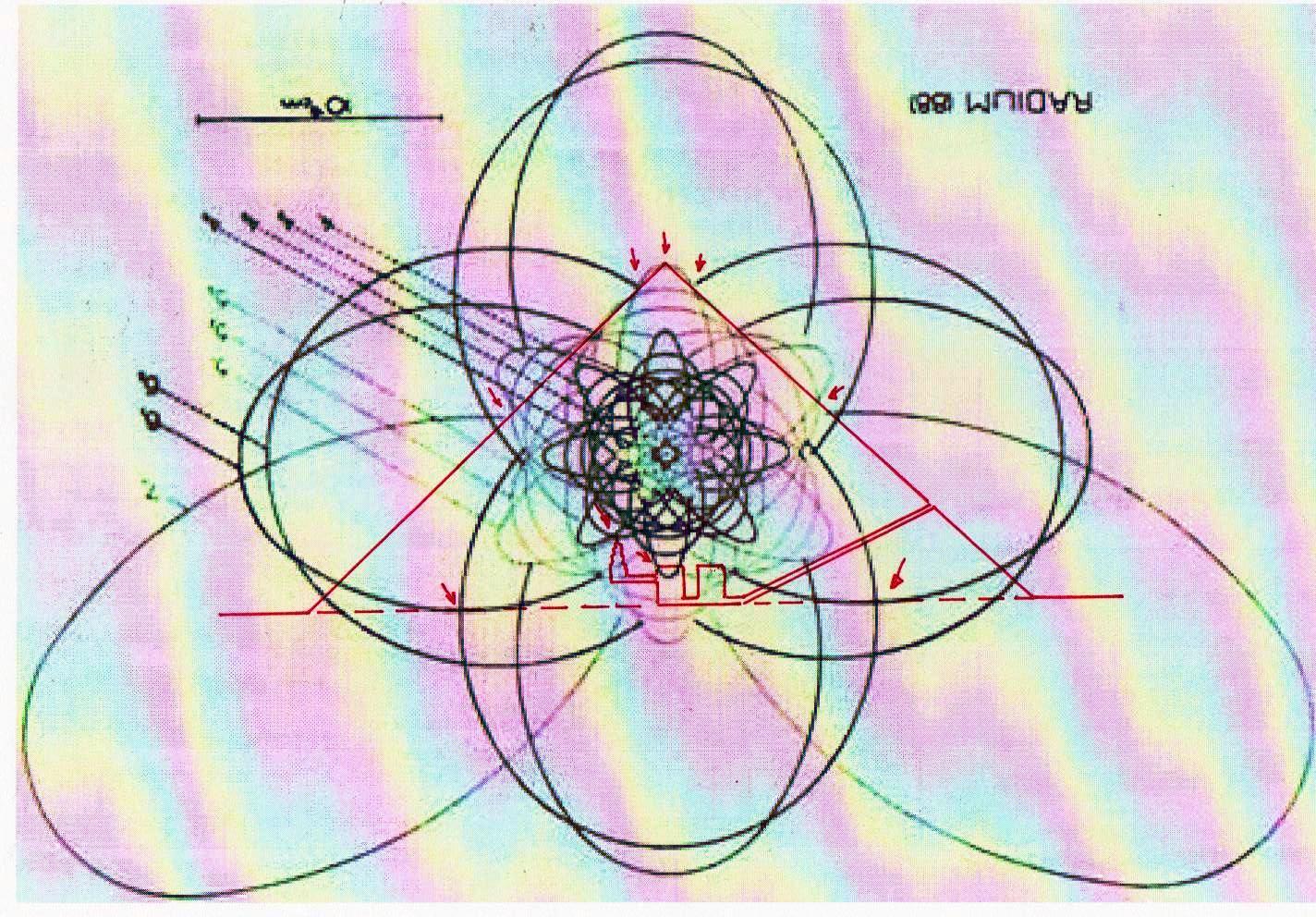
Ahora bien, como hemos señalado anteriormente, si se supone que las constantes de nuestras leyes científicas se pueden (o se deben: eso no tiene mucha importancia) traducir en funciones de π y ϕ, sale de esto como consecuencia que también los valores asumidos por las variables se convierten – aunque de manera complicada – en funciones de estos dos valores fundamentales. Por lo tanto, no es excluido de ninguna manera que, después de descubrir que en la Gran Pirámide está cifrado el diagrama bidimensional del espacio-tiempo, un día se pueda descubrir allí también alguna versión codificada de la mecánica cuántica. Más aún, a decir verdad, sería muy extraño si no fuera así, ya que realmente parece muy difícil de atribuir a una civilización cualquier versión de la mecánica relativista sin una comprensión paralela del mundo de las partículas, dado que – al menos en el ámbito de nuestro mundo histórico – estos dos campos de la física se han investigado más o menos por las misma personas y más o menos en el mismo período (aunque los debates y controversias relacionados con la mecánica cuántica han estado ocurriendo desde hace varias décadas, mientras que la mecánica de Einstein fue aceptada más rápidamente y con menos conflictos). De hecho, indicios de la presencia de este tipo de teorías podemos mostrarlos ya en este artículo. Si, como en las imágenes de abajo, probamos a superponer el perfil de la Gran Pirámide a el del modelo cuántico del átomo de hidrógeno desarrollado por Bohr, parece que una vez más podemos obtener sistemas de congruencias que no aparecen en absoluto casuales

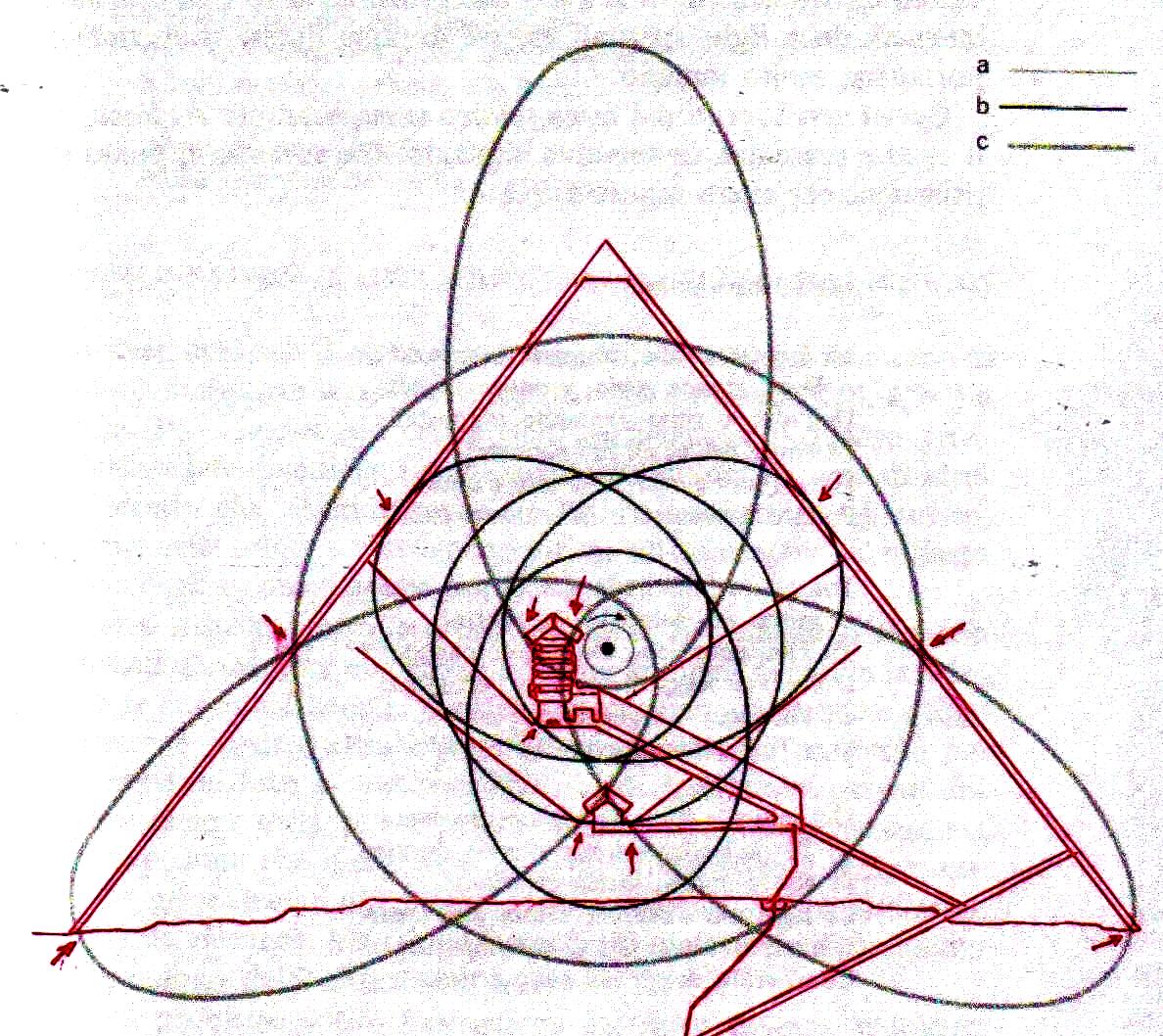
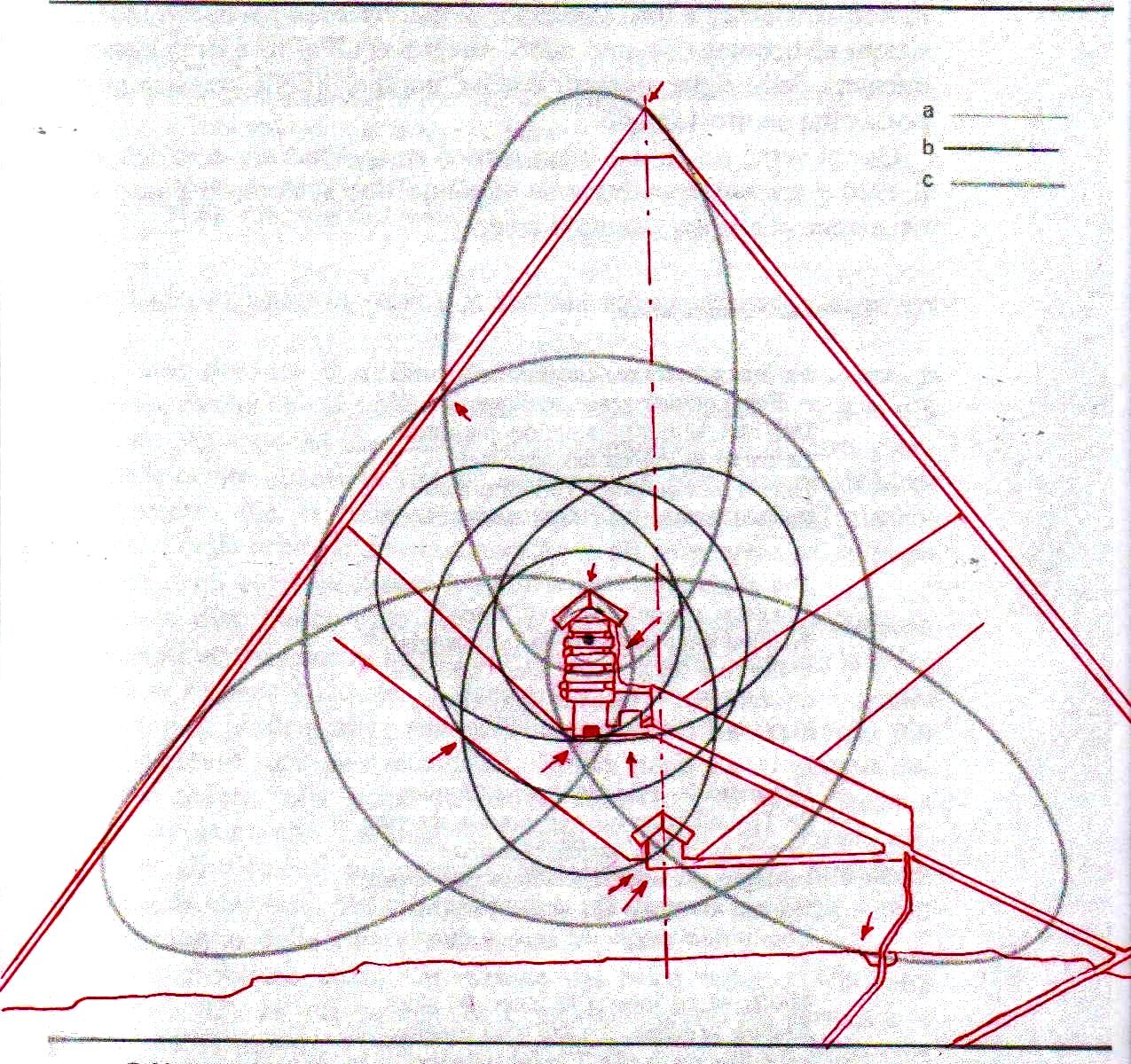
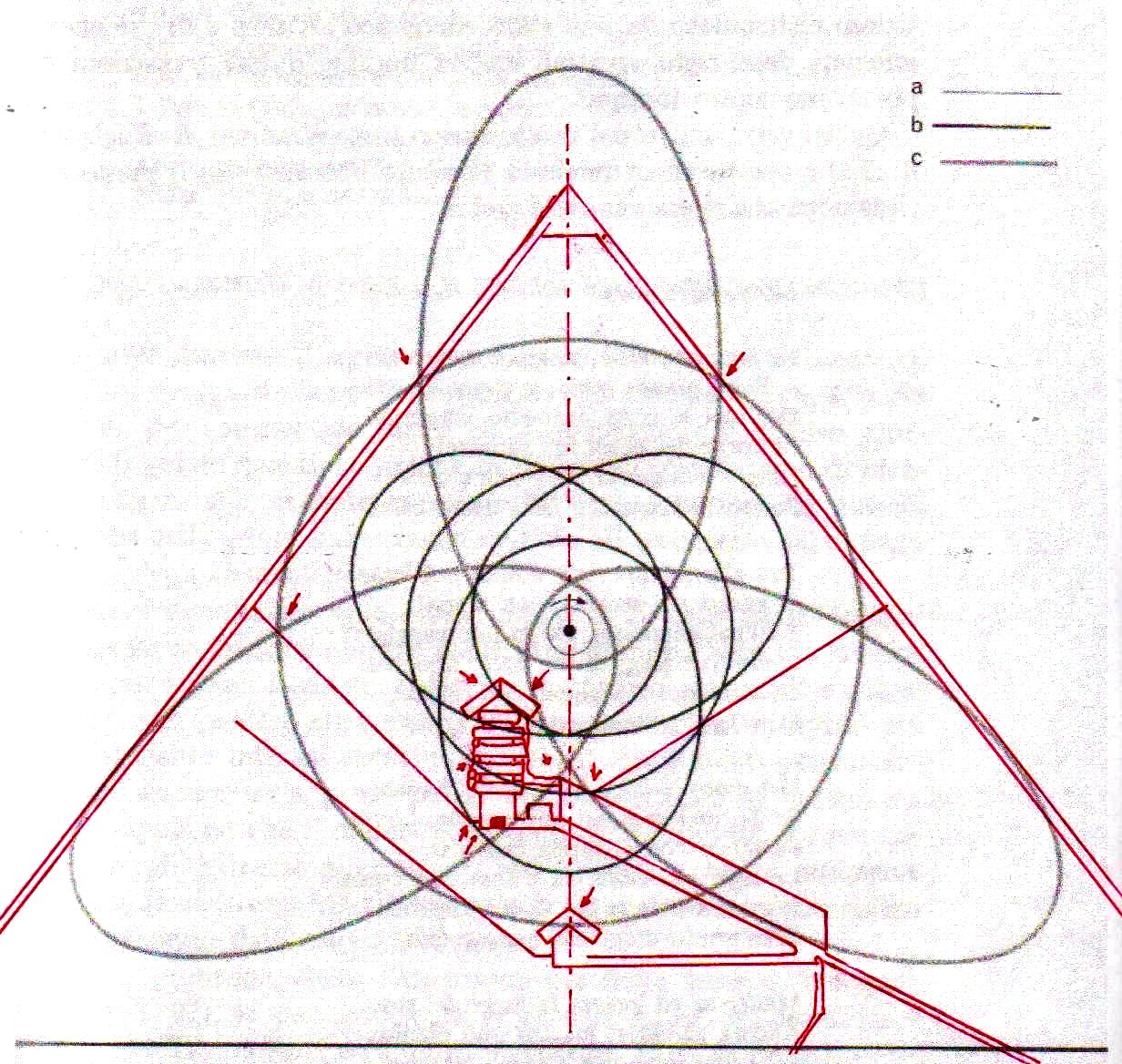
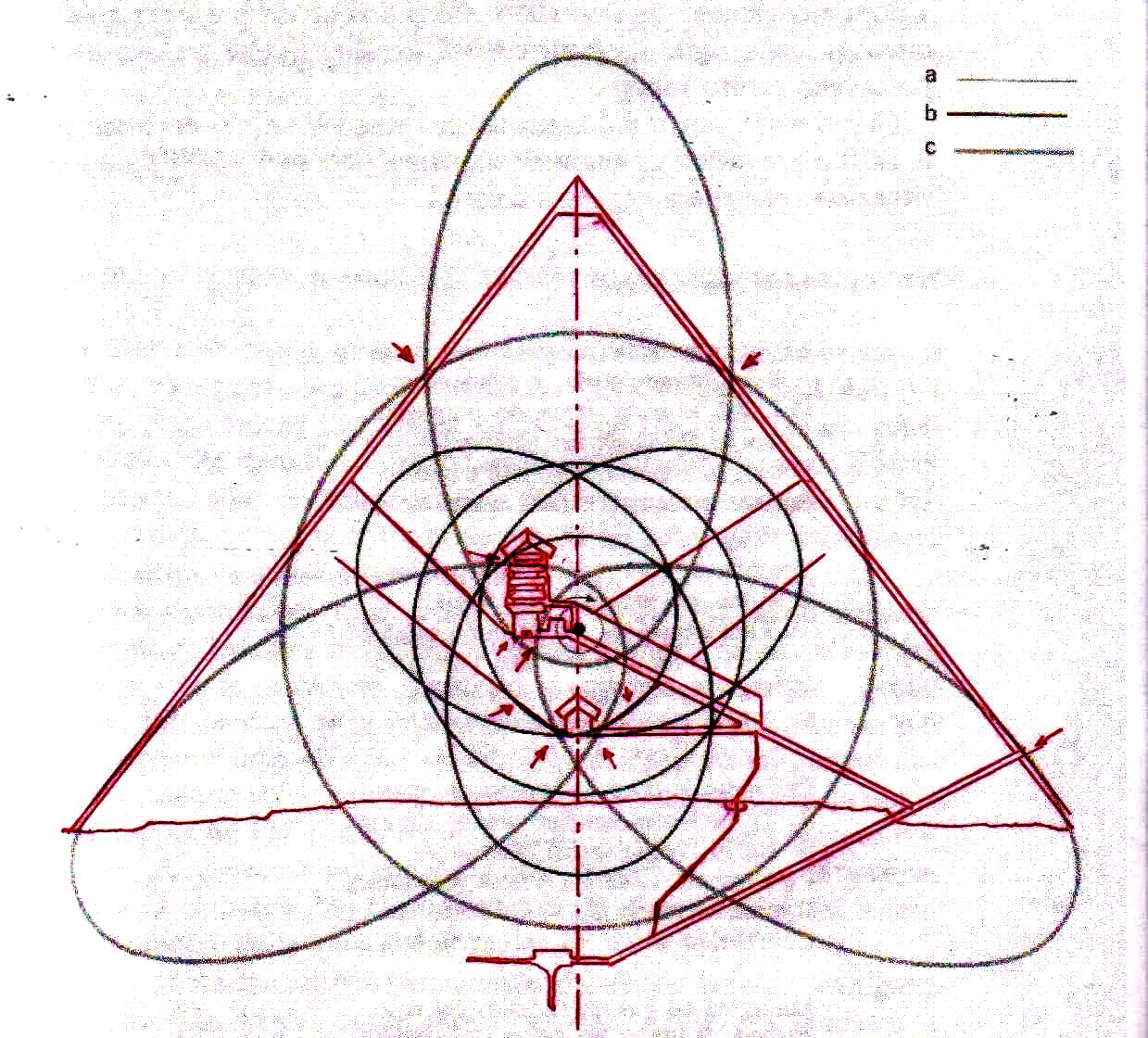
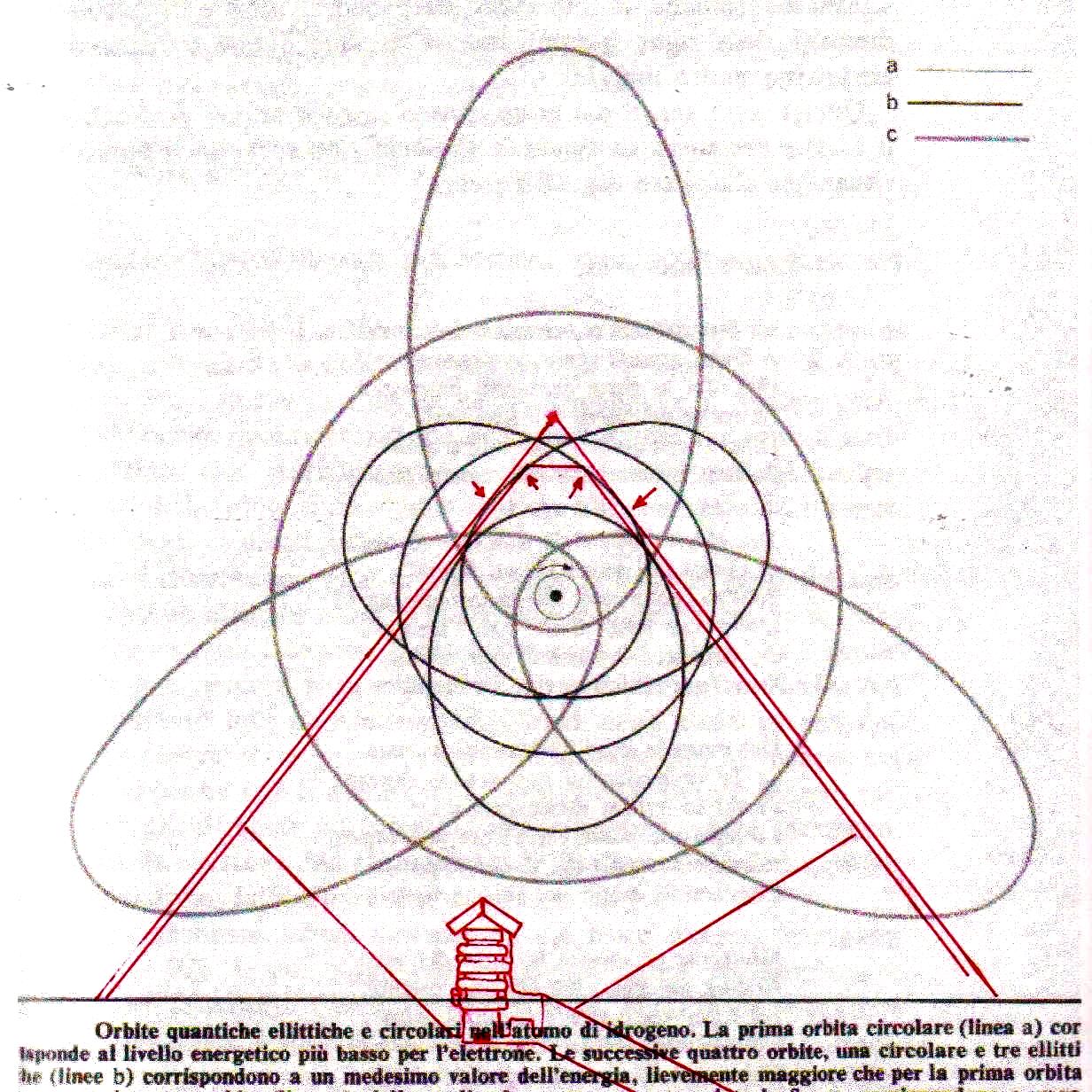
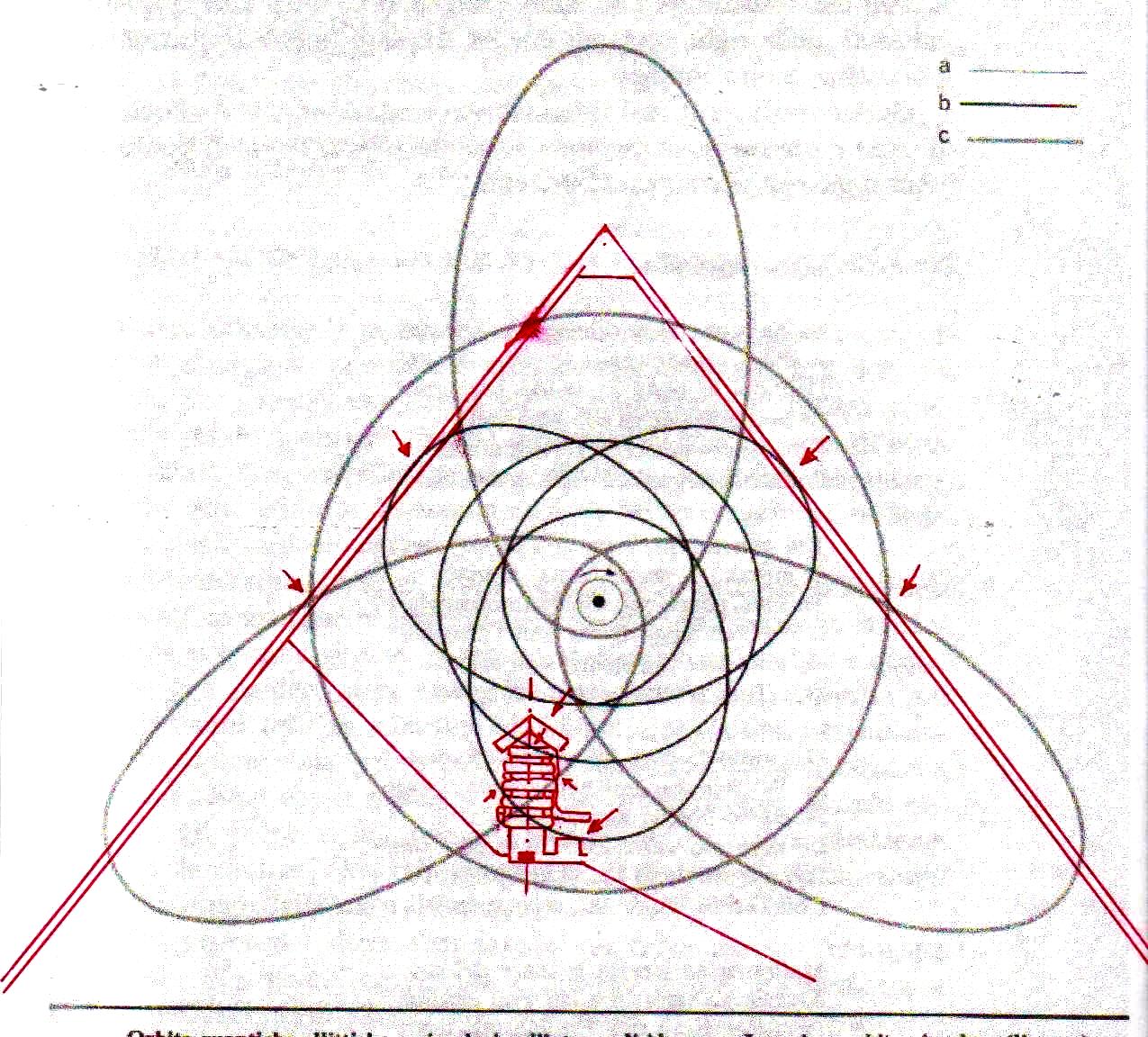
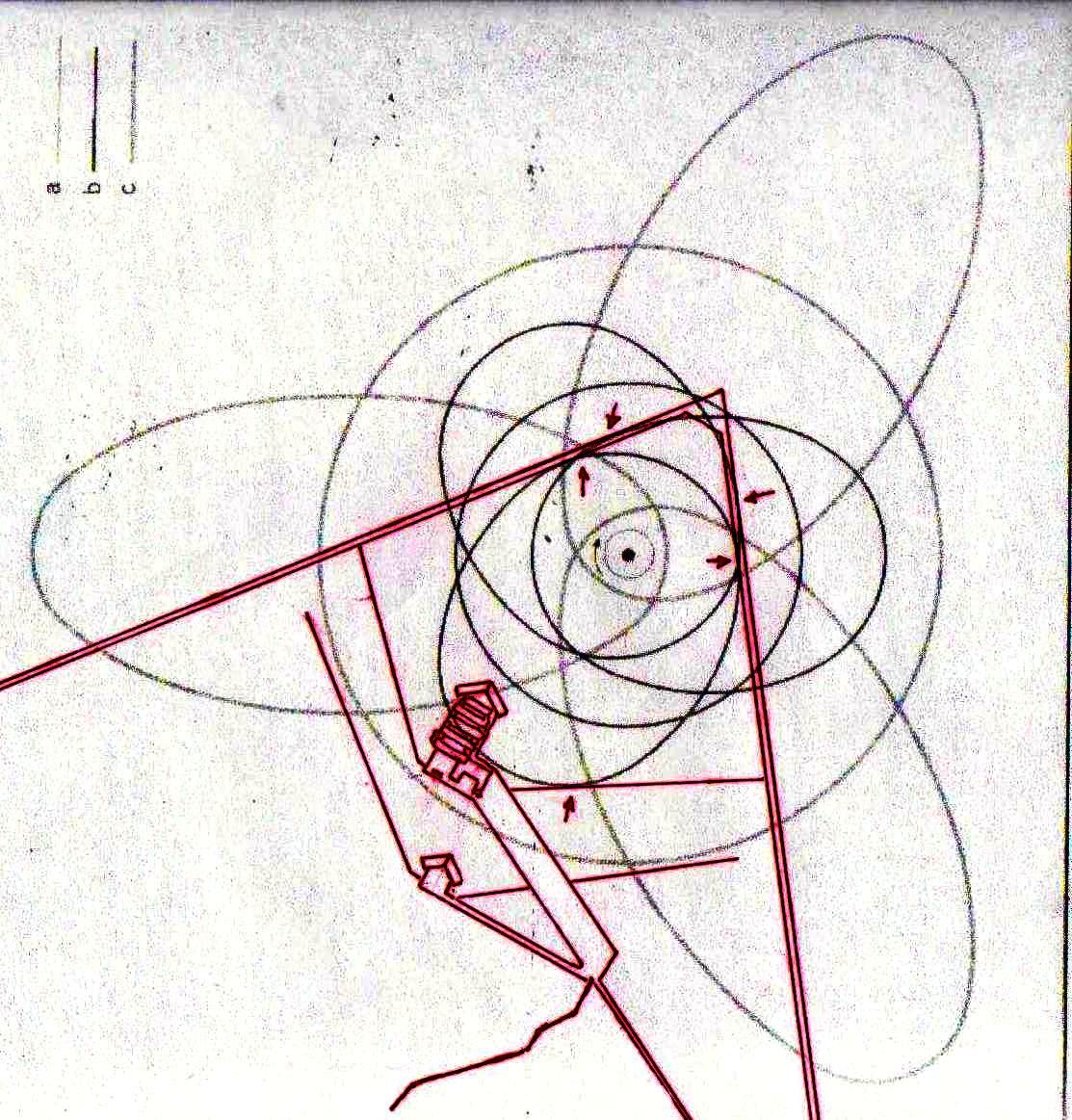
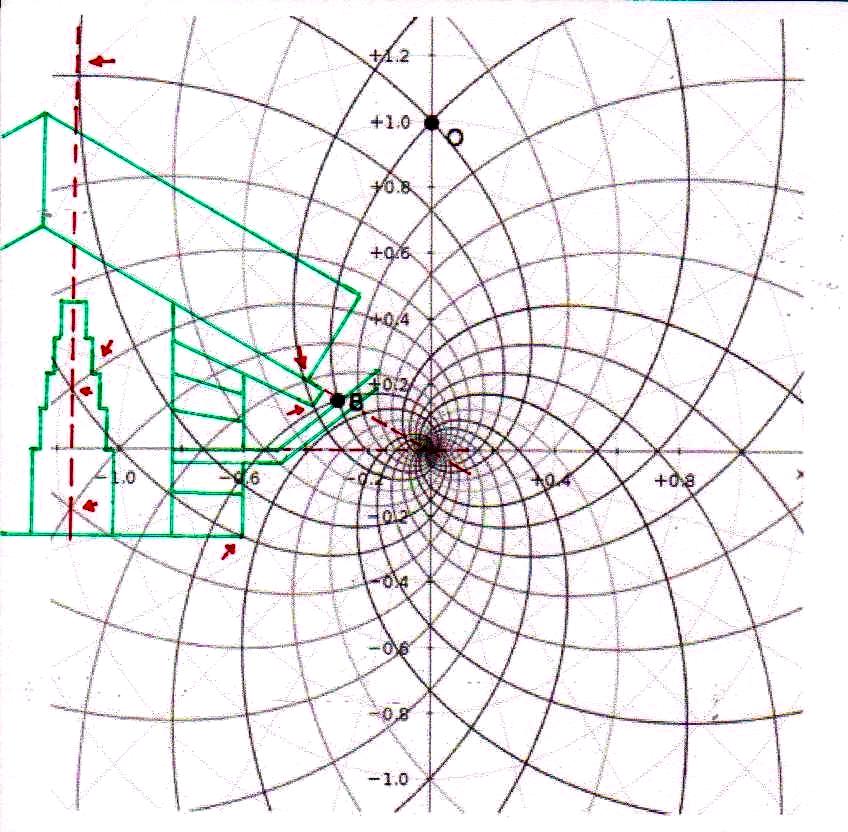
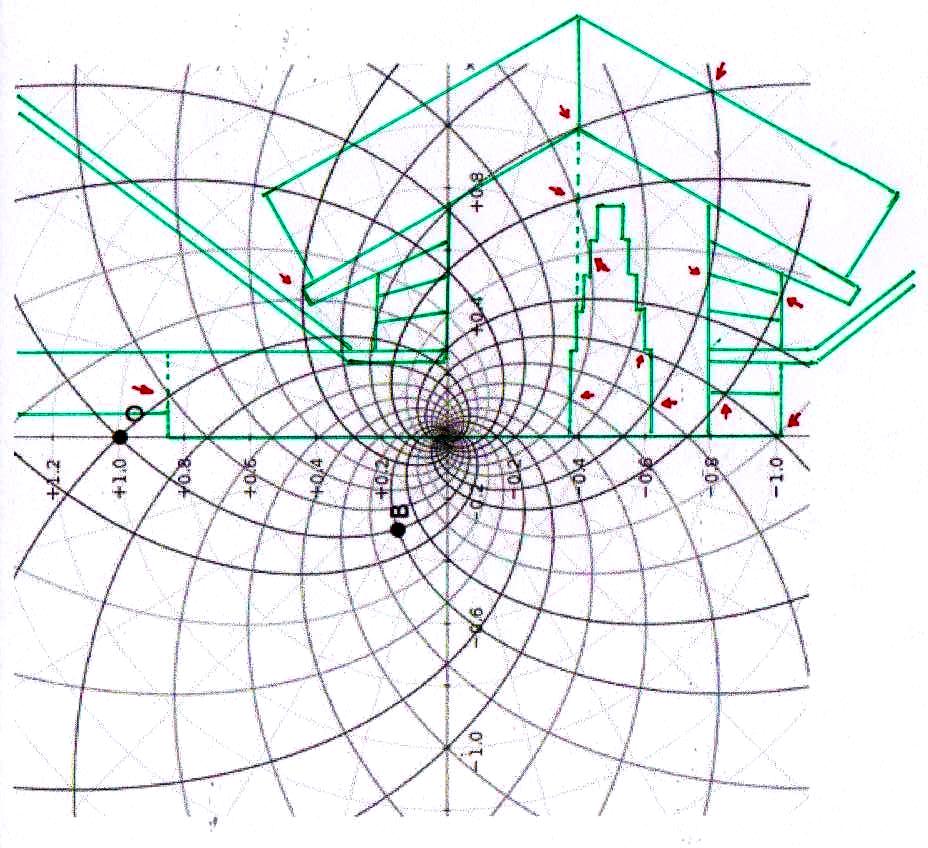
Estos sistemas de congruencias ya en sí mismos son bastante impresionantes: la inclinación de la Pirámide y las disposiciones de sus partes internas parecen poseer características tales como para poder identificar puntos característicos del diagrama de Bohr (y viceversa). Y esto solo ya parece un indicio muy importante de que la mecánica de las partículas se ha codificado de alguna manera en el monumento junto con el espacio-tiempo relativista. Pero después de lo que hemos visto hasta ahora, nadie se sorprenderá al descubrir que un sistema semejante de superposiciones se repite – cambiando la escala de proyección – también a nivel de la Cámara del Rey. En las imágenes que siguen podemos ver cómo, apoyando segmentos de órbitas sobre segmentos del perfil de las Cámaras Superiores (que hasta ahora se pensaban dejadas en su estado crudo) el diagrama del átomo en su conjunto encuentra de nuevo un sistema de congruencias con todo el resto de la estructura. Y esto parece significar de nuevo que las partes crudas o que parecen dañadas (como la esquina del sarcófago) también son la expresión perfecta del código y por lo tanto de esas leyes científicas de que la Gran Pirámide se convirtió en la imagen arquitectónica

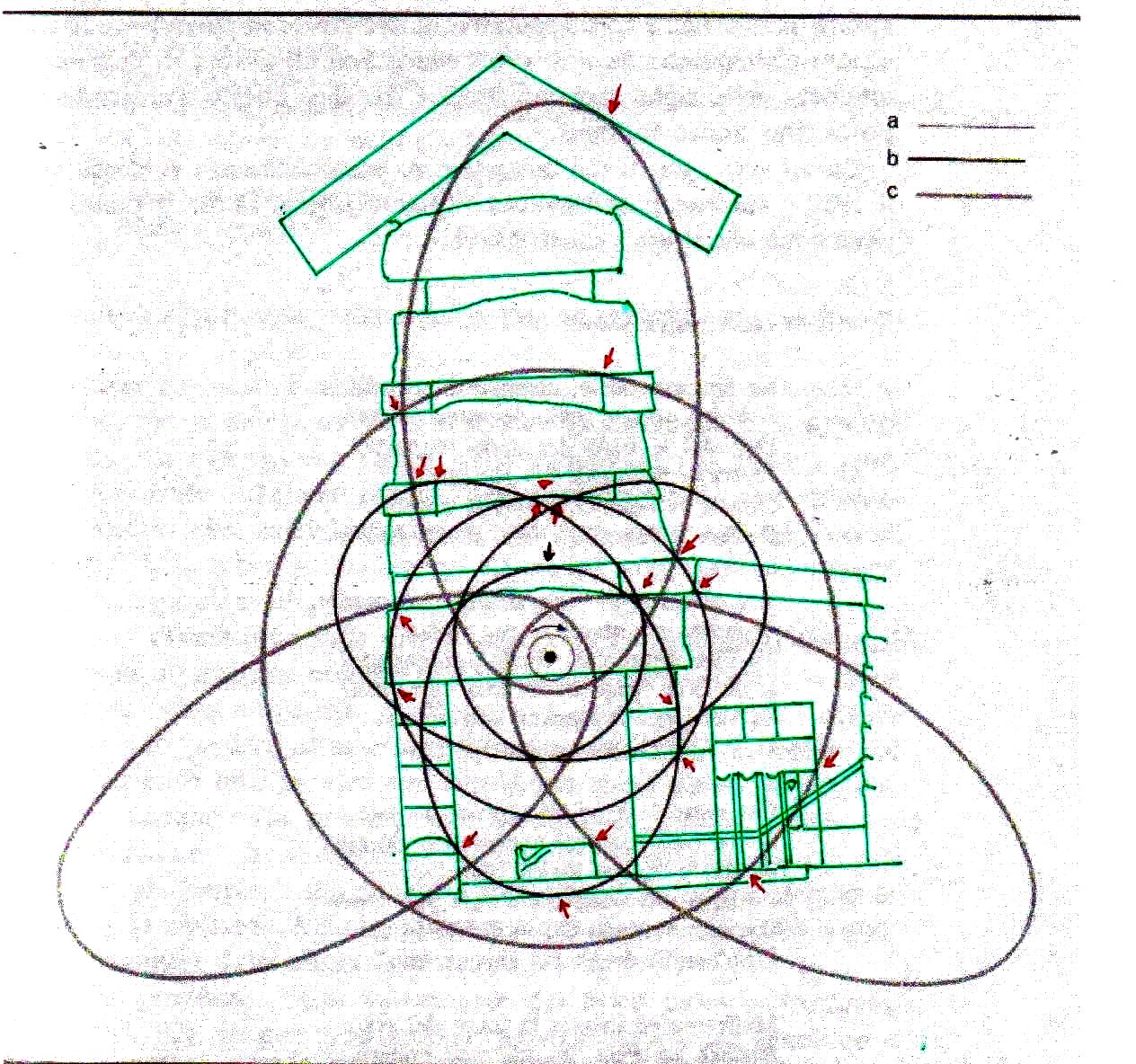
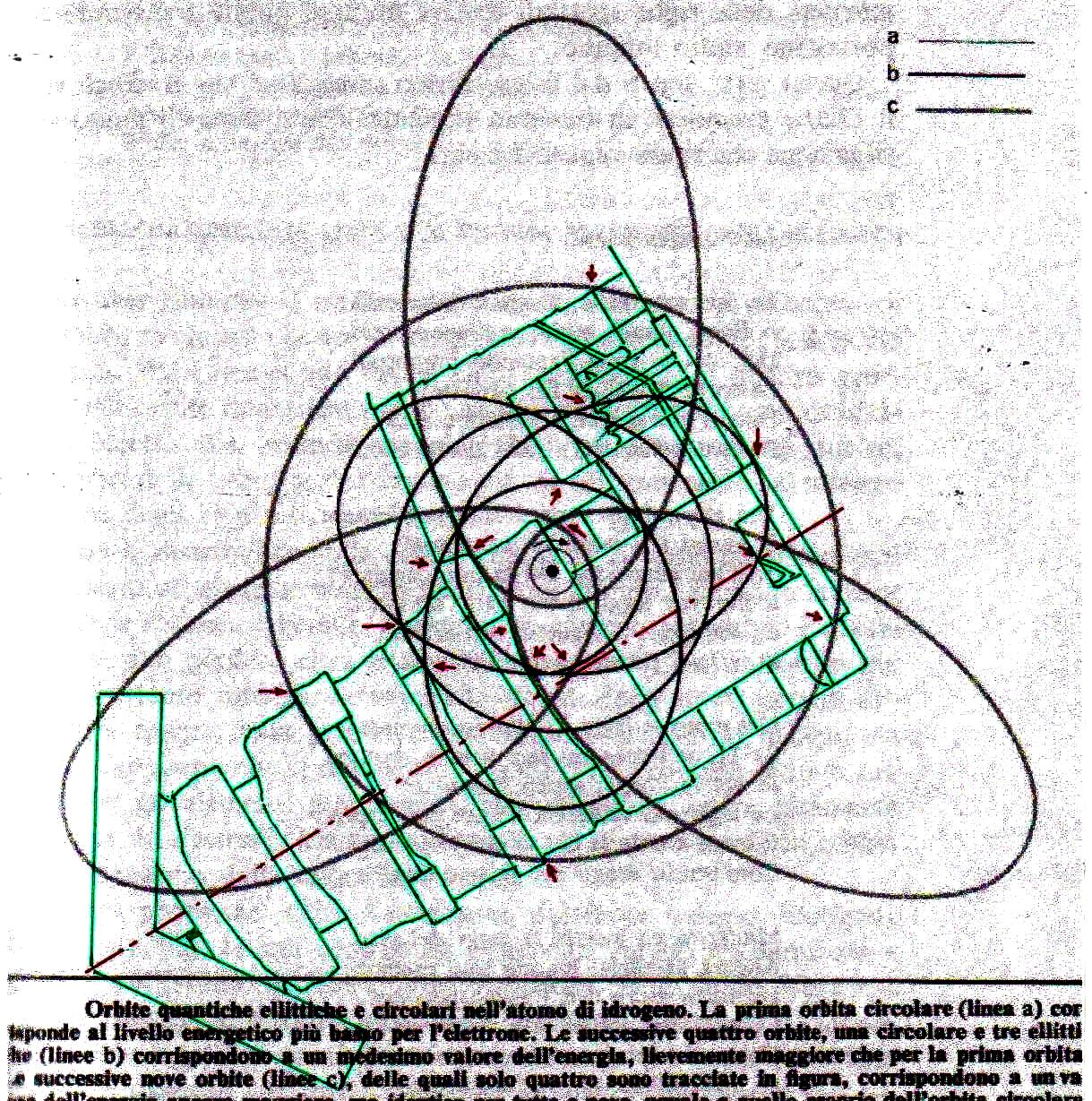
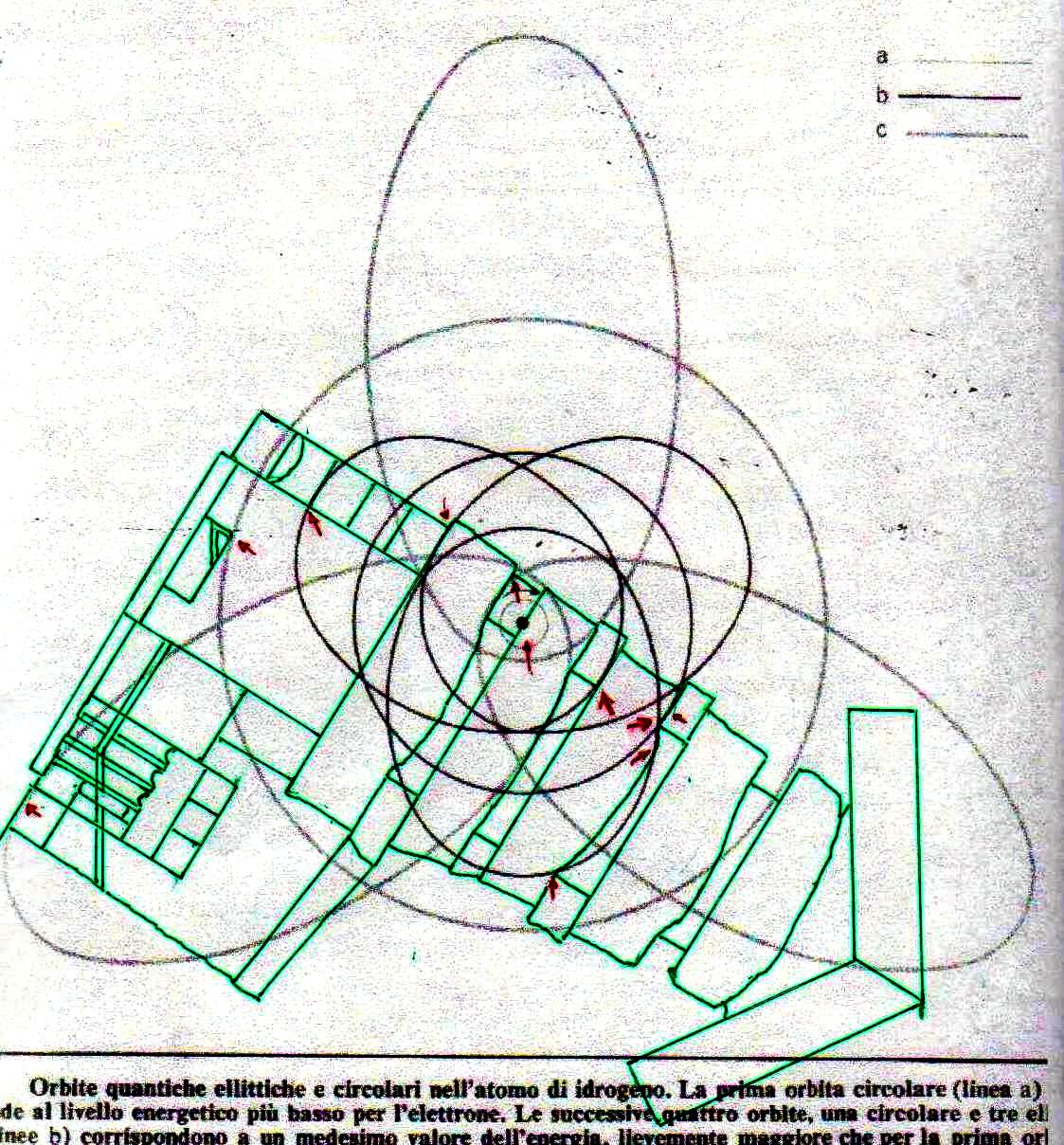
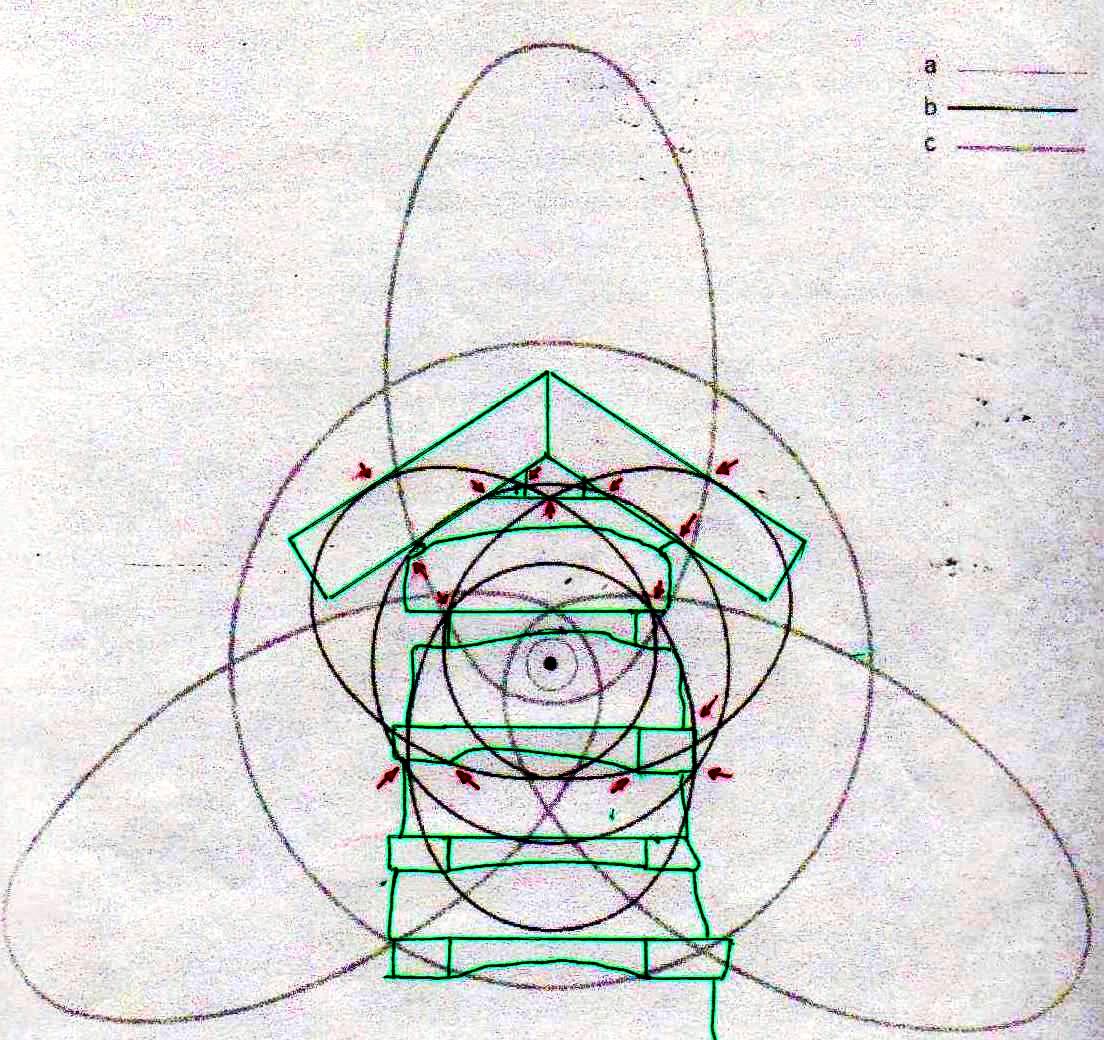
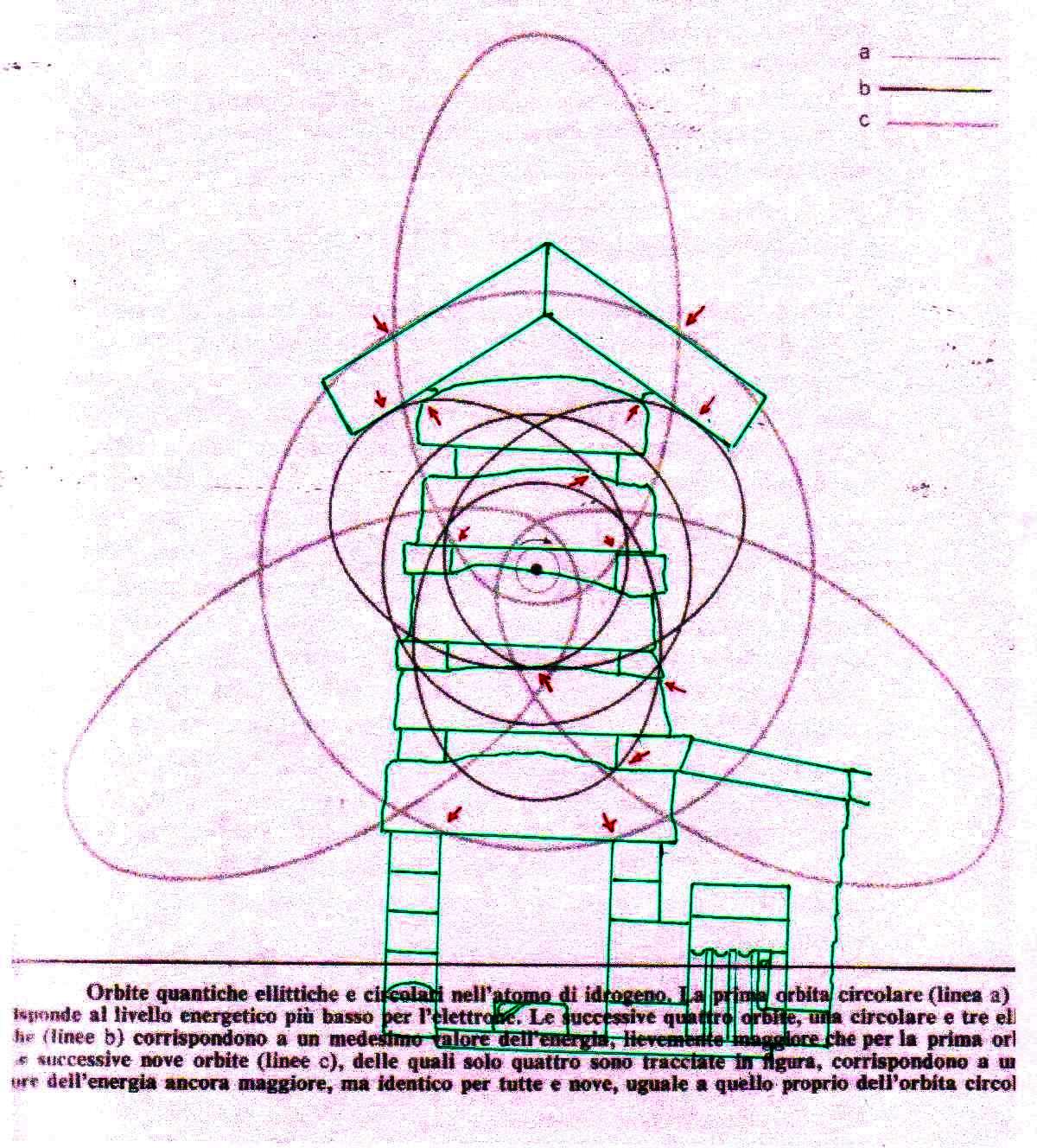
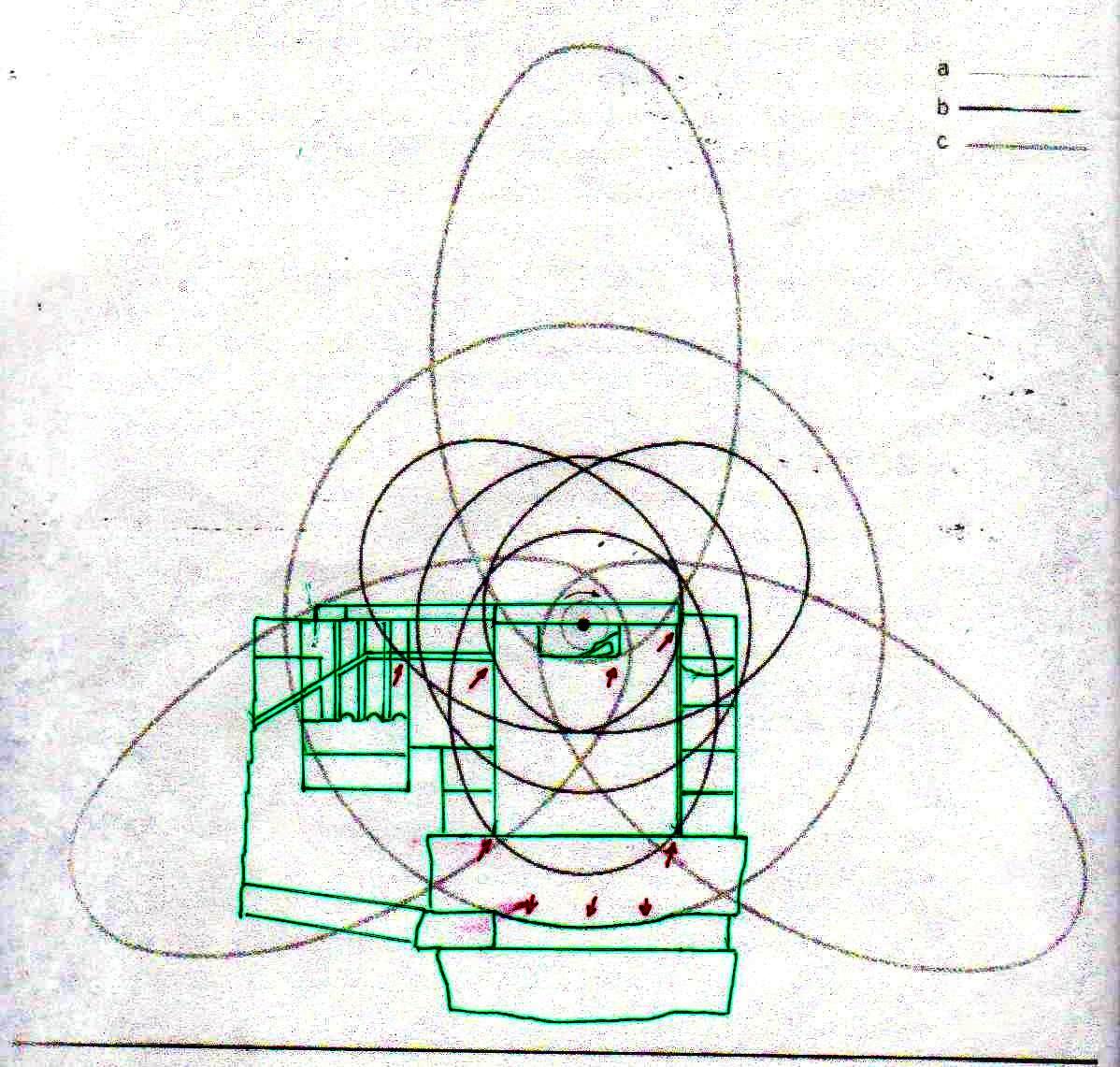
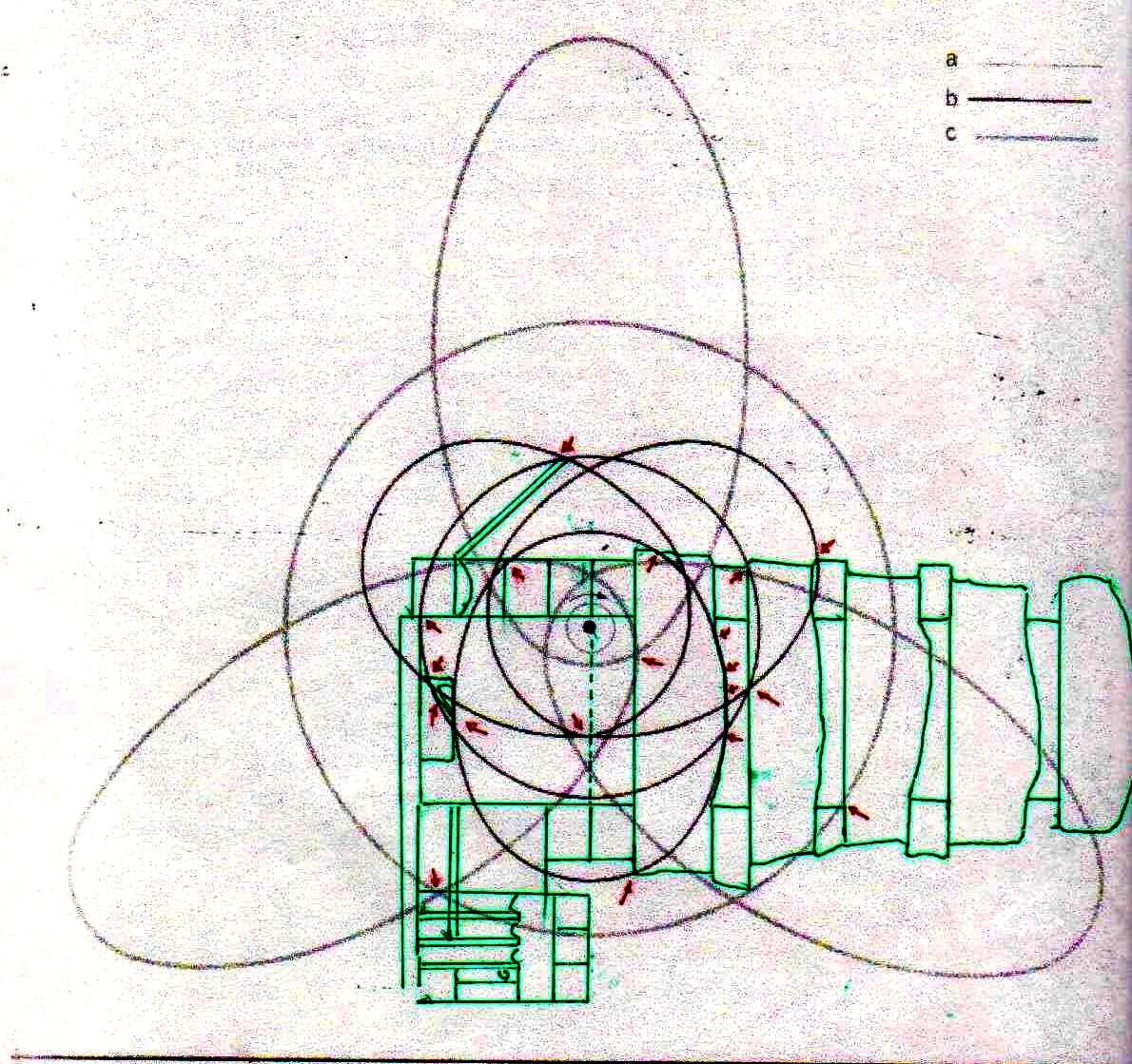
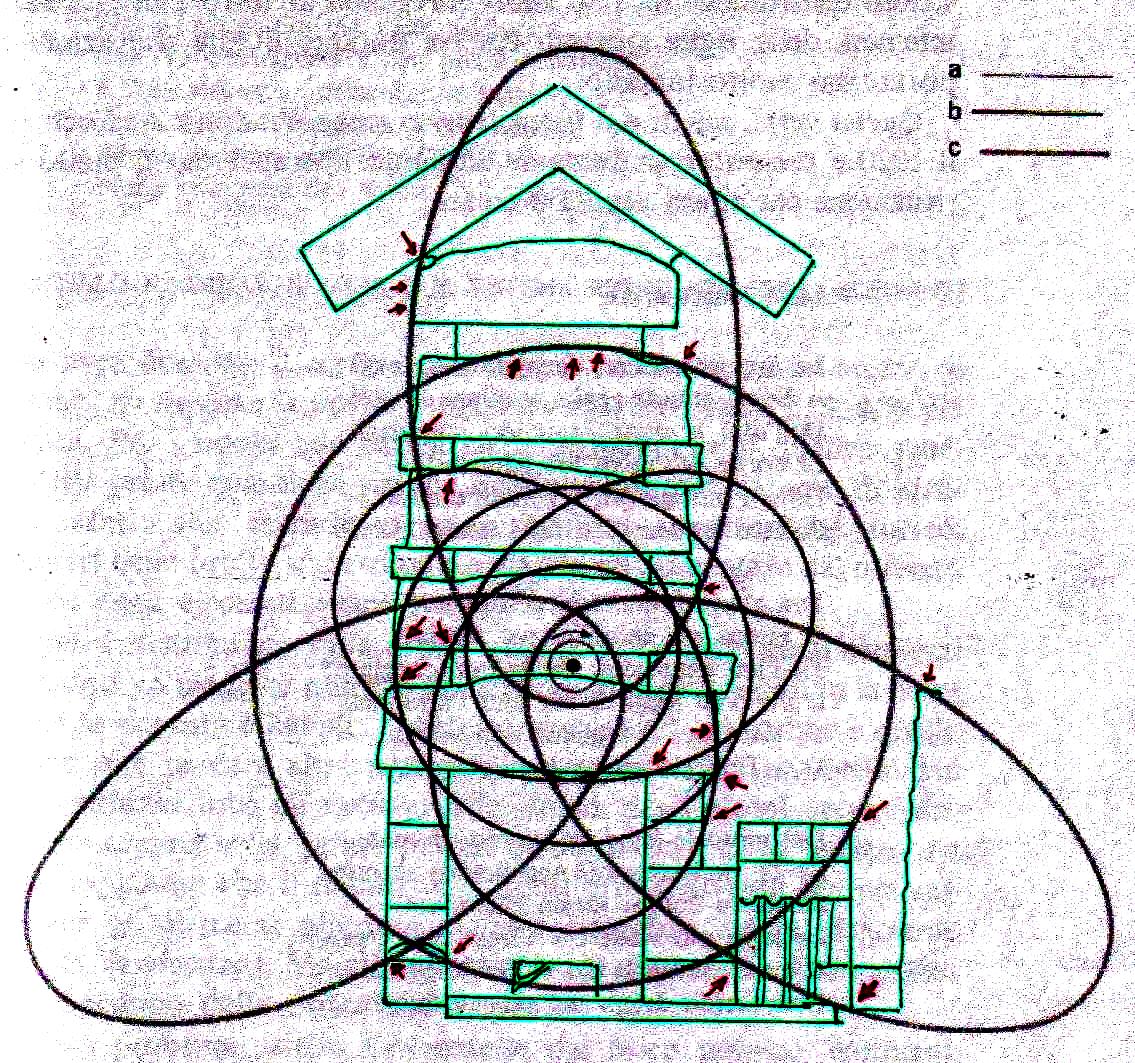
8) El análisis de estas imágenes lleva a suponer inductivamente de manera bastante seria que la Gran Pirámide y los relieves del Antiguo Egipto se han diseñado por medio de un código geométrico compatible tanto con el diagrama bidimensional del espacio-tiempo como con el modelo cuántico del átomo de hidrógeno. De esto deriva como consecuencia que

1) el modelo cuántico del átomo de Bohr debe encontrar sistemas de congruencias también en el diseño de las estelas

2) tanto el diagrama del espacio-tiempo como el del modelo cuántico del átomo de Bohr deben tener puntos en común

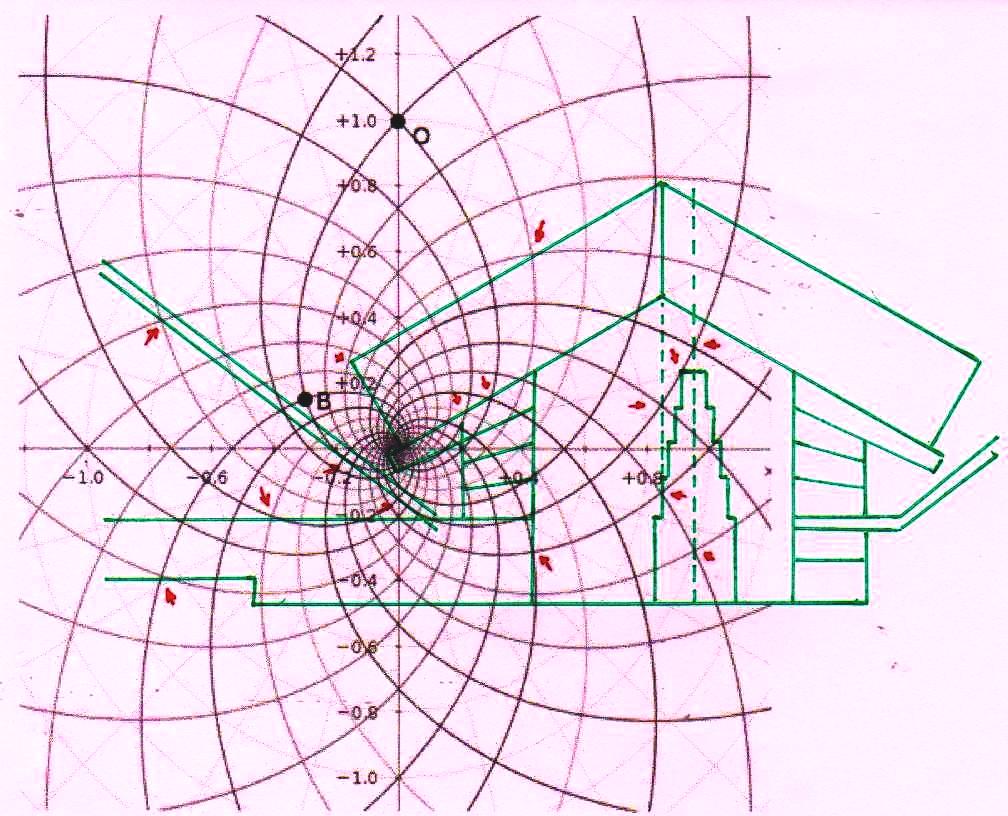
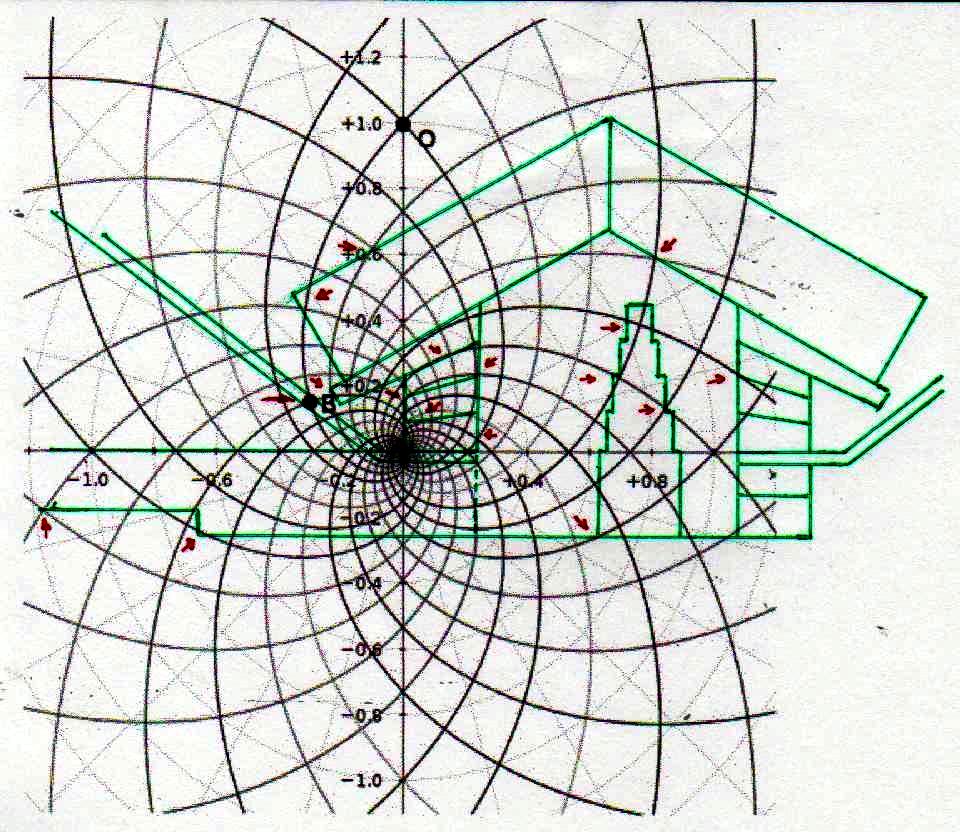
Pues bien, a través de la imágenes que siguen estamos en condición de demonstrar que estas dos inducciones aparecen fundadas, ya que el sistema de intersecciones que ya hemos visto se puede reconstruir no sólo desde lo que ya hemos analizado sino también por otros dos modelos diferentes de átomo, que parecen tener algo que ver tanto con la estructura de la Gran Pirámide en su conjunto como con la de la Cámara del Rey y la Cámara de la Reina

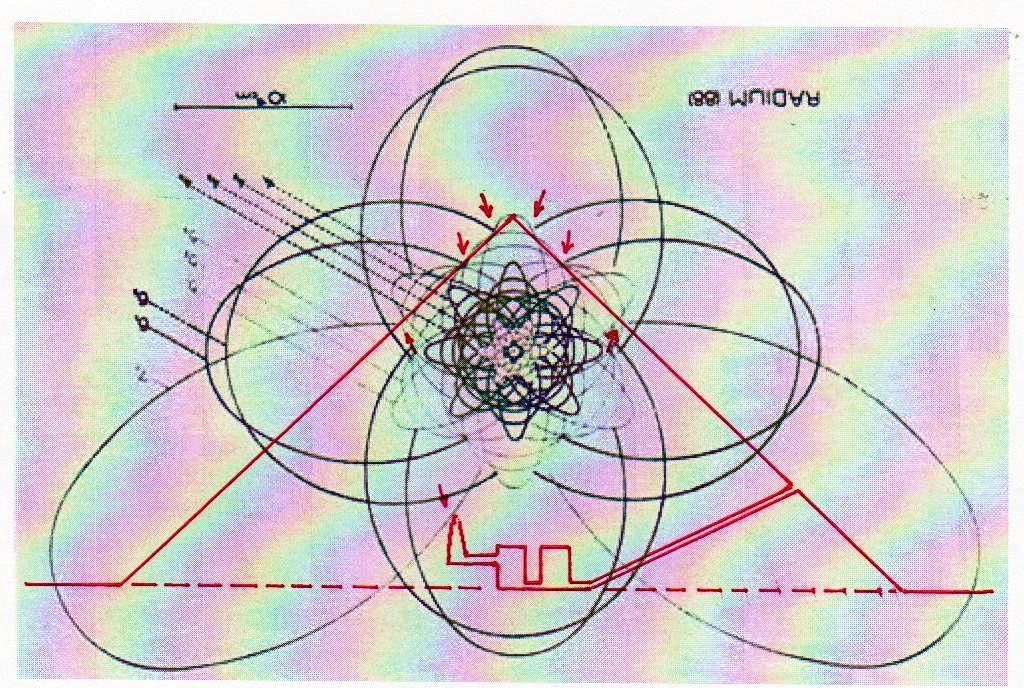
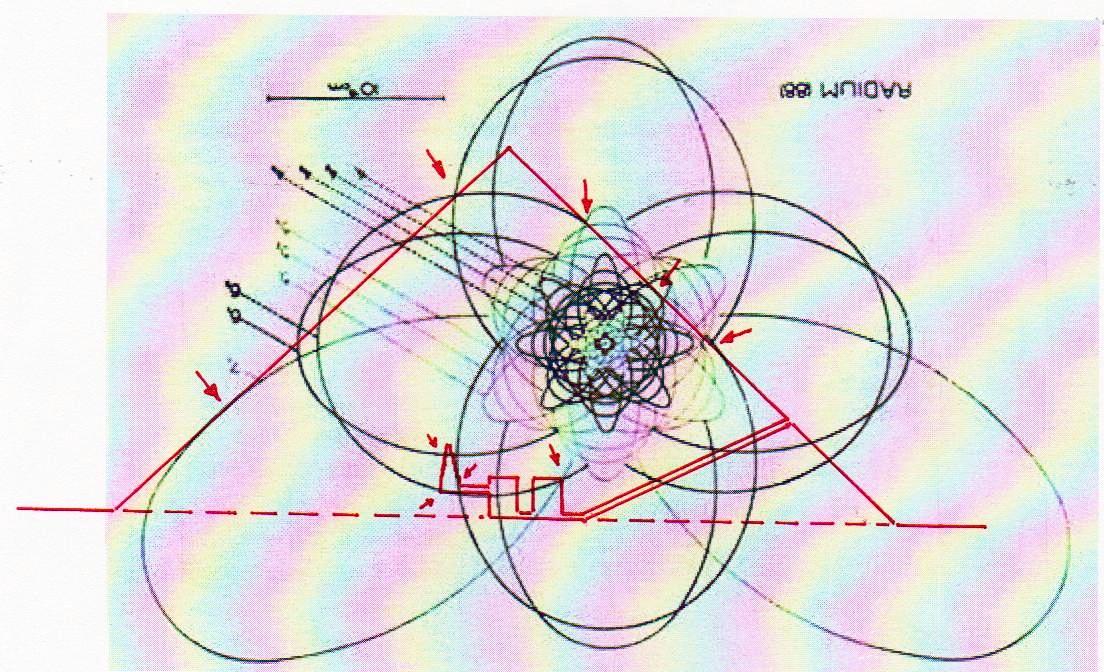
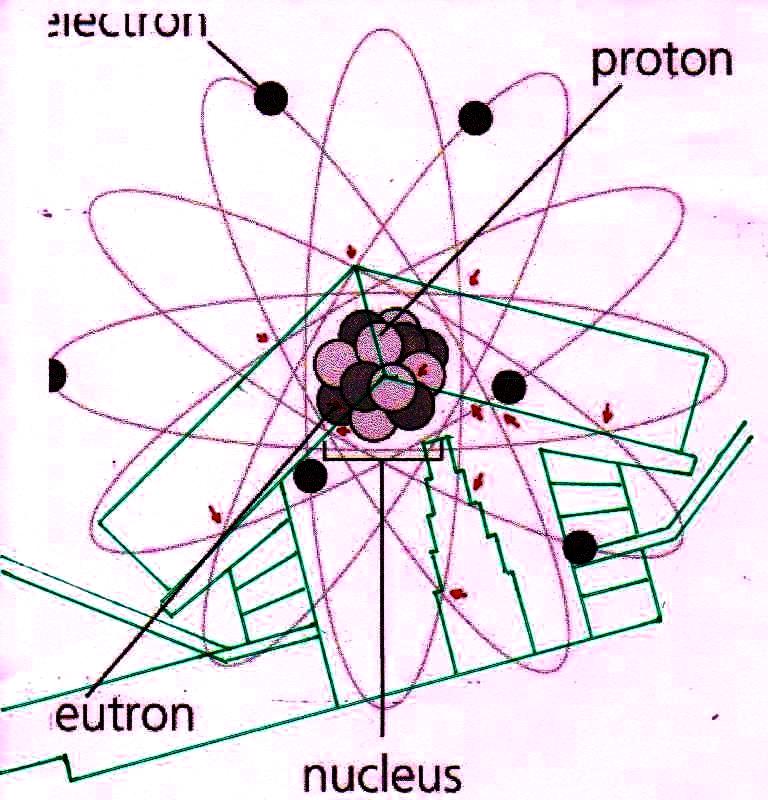
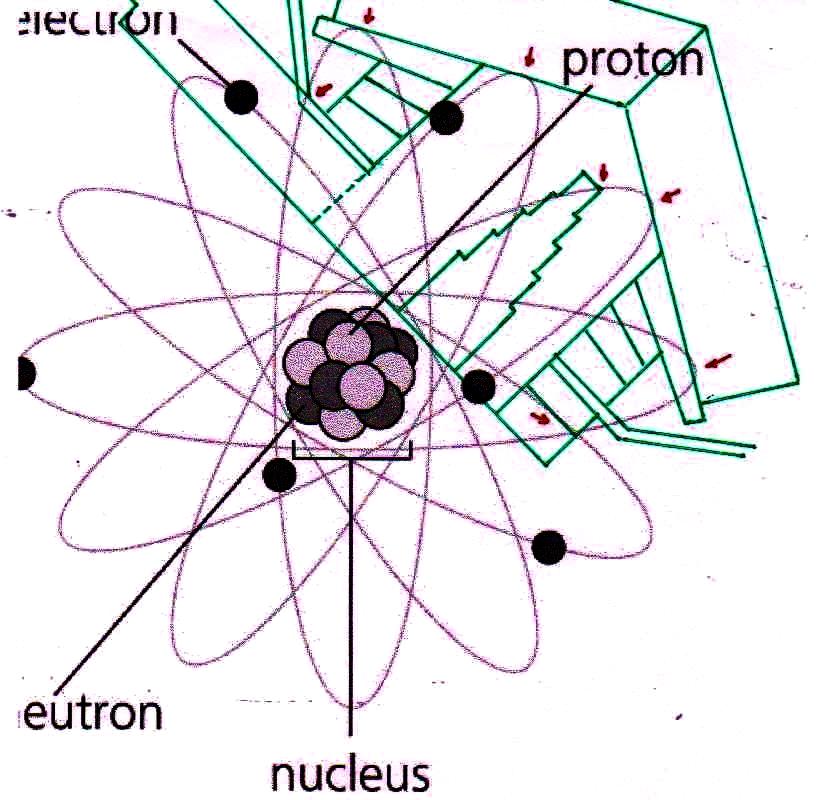
Somos conscientes que imágenes de este tipo y las hipótesis que parecen casi naturalmente derivar de ellas, son capaces de dejar bien perplejos. En particular, la segunda imagen – la en la que el diagrama del espacio-tiempo se superpone a el del átomo – parece sugerir que las dos teorías, que a nivel lógico-matemático se consideraron siempre en competencia y contradicción, pueden en cambio, al menos a nivel de la representación geométrica bidimensional, encontrar puntos de contacto de al menos una aparente relevancia. Pero hay que reconocer que no está claro lo que esto significa en realidad a nivel científico (y por lo tanto al de la filosofía de la ciencia). Lo que aparece que podemos deducir de estos sistemas de superposiciones es que las órbitas reales o posibles de los electrones alrededor del núcleo se dibujan y escanden según un ritmo dictado también por el número de oro, así como por el Pi griego: es un poco lo que sucede en el caso de la distribución de las hojas alrededor de las ramas y otros fenómenos parecidos. Este hecho podría tener cierta importancia, ya que las órbitas de los electrones tienen un significado relacionado con la longitud de onda (recordemos que la órbita de un electrón alrededor del núcleo sólo puede ser un múltiplo entero de la longitud de onda) y su estado de energía. Así que puede ser que estos dos factores estén relacionados entre sí por una ecuación en la que el número de oro juega un papel decisivo, al menos por lo que podemos intuir por las imágenes que hemos visto. Pero, por supuesto, estas afirmaciones tienen por el momento un valor puramente heurístico, y la única prueba posible de su verdad la podremos tener sólo cuando vamos a ser capaces de describir de manera exacta la relación entre estas cantidades por medio de una ecuación en la que el número de oro tenga de hecho y no sólo como hipótesis un significado decisivo. Todo lo que podemos decir en este momento es que los antiguos Egipcios, a través de sus estelas y arquitectura, muestran que han utilizado un código geométrico basado en π y ϕ, que puede sugerir puntos de contacto de algún tipo entre estas dos teorías. Después de lo que hemos visto no podemos ni siquiera descartar por completo que la Gran Pirámide represente geométricamente aquella teoría de los campos unificada que en el Occidente moderno estamos todavía buscando a tientas. Tal vez el diagrama del espacio-tiempo desarrollado por Fappalà tiene un significado más profundo de lo que el mismo autor imaginó y por lo tanto merece un estudio cuidadoso, que posponemos para otro momento y trabajo.

CUARTA PARTE: HUELLAS DE UNA CIENCIA ANTES DE LA CIENCIA EN LA ICONOGRAFÍA SAGRADA DEL ANTIGUO EGIPTO Y EN LAS ESTRUCTURAS MEGALÍTICAS DE LA PREHISTÓRIA

1) Por tanto, un primer punto de llegada de nuestra investigación es la hipótesis de que π y ϕ eran codificados en el arte sagrado del Antiguo Egipto, porque de estas constantes geométricas
1) se pueden derivar las constantes y por lo tanto los diagramas de todas estas leyes científicas que permiten al hombre de tener poder sobre la naturaleza, en particular la física relativista y la mecánica cuántica
2) como se ha visto en The Snefru Code part. 4 y como veremos mejor al final de este trabajo, estos dos números son también los que caracterizan la estructura de esos ciclos cósmicos que podemos considerar fundamentales para la religión y por lo tanto para la cosmovisión del hombre prehistórico.
Pues, nuestra hipótesis es que en tiempos muy antiguos ciertamente ha existido una técnica avanzada, que operaba con las mismas fuerzas utilizadas por la técnica moderna (y posiblemente también con al menos una otra fuerza que no hemos descubierto todavía, es decir el signo menos del campo gravitacional; pero vamos a tratar mejor este punto al final del artículo). Sin embargo, tal vez sea útil señalar desde el principio que, a pesar de los puntos en común que encontramos, por ejemplo, a nivel del concepto del espacio-tiempo, por los restos arqueológicos también estamos obligados a suponer que la técnica derivada de la ciencia antigua era diferente y/o más avanzada que la nuestra, al menos en el campo del tratamiento de la piedra (que es un indicio de un posible mayor desarrollo también a nivel teórico). Además, las componentes de estas máquinas de muchos milenios atrás tuvieron que ser hechas de materiales perecederos o incluso biodegradables, porque, de lo contrario, no se entiende por qué no se han encontrado los restos de todos estos materiales artificiales resistentes a los agentes atmosféricos – tales come el acero inoxidables – que en nuestras máquinas están presentes en abundancia. Además, por lo que se puede constatar en el momento, estas herramientas se utilizaron sólo para construir obras sagradas, estrechamente relacionadas con su fe religiosa, al menos si pensamos en los edificios de piedra, que son los únicos que han podido cruzar los muchos milenios que nos separan de su diseño y construcción. Pues, parece que de esto podemos deducir que los que construyeron monumentos como las pirámides de Guiza y Dahshur sintieron el poder asumido por la ciencia como un fragmento del poder divino, mientras que hoy este poder no es considerado de ninguna manera como sagrado, ya que se considera – por lo menos por la mayoría de los científicos – que ciencia y fe tienen que ir por caminos que no deben cruzarse nunca sin perjudicarse recíprocamente. Pero al poco rato vamos a insistir más en este tema, que adquiere una importancia que parece realmente decisiva para buscar de comprender el espíritu de los hombres de la Edad de la Piedra, que en este punto se manifiesta tan diferente de la nuestra.

2) Pasando a tratar de los testimonios arqueológicos directos y indirectos de esta que hemos definido como “la ciencia antes de la ciencia”, si del campo del análisis geométrico-matemático de las estelas del Antiguo Egipto y de la Gran Pirámide nos volcamos al análisis de su inmediato contenido iconográfico, vemos que efectivamente algunos de los jeroglíficos – mejor conocidos como “lámparas de Dendera” – por los cuales no se ha encontrado una explicación realmente convincente, parecen aludir a algunos instrumentos relacionados con el electromagnetismo. A continuación podemos ver dos imágenes de un relieve muy famoso, del cual se notó la extraña semejanza con un aparato de rayos X de la modernidad. A la luz de lo que hemos visto arriba, una interpretación de este tipo no sería más anti-histórica y, de hecho, encajaría perfectamente con el contexto de una ciencia muy antigua que ha llegado a resultados similares a los nuestros de otras maneras, y que con otros medios la habría aplicada para objetivos totalmente diferentes de aquellos para los que nosotros la utilizamos hoy

Todas estas hipótesis – si estén verificadas – nos permitirían de arrojar luz también sobre otro hecho muy extraño, que se produjo en el siglo pasado, por el que también no fueron nunca encontradas explicaciones satisfactorias y que de una manera indirecta está relacionado con la cultura egipcia antigua. Estamos hablando de la construcción de Coral Castle – una gran villa hecha de bloques de granito, uno de los cuales llega al peso realmente asombroso de 30 toneladas. Esta villa fue construida en un lugar aislado por un emigrado ruso, llamado Edward Leedskalnin, sin la ayuda de nadie (excepto por el transporte de las piedras al lugar). Hasta la fecha no podemos formular hipótesis fundadas cómo fue posible que un solo ser humano fuera capaz de crear una obra tan colosal usando sólo equipos de elevación muy modestos, que después se encontraron en su obra. Pero Leedskalnin afirmó que había descubierto la forma por la que los antiguos Egipcios eran capaces de levantar pesados bloques de piedra y que él había usado tal forma para colocar aquellos con que construyó su villa. Más allá de las historias que se cuentan sobre el tema, en su obra se encontraron herramientas de que no se puede entender la función, una de las cuales – un imán giratorio a manivela – se parece de una manera característica a unas vasijas que se hallaron en Guiza. En las siguientes imágenes se puede observar el imán y las vasijas uno cerca de las otras

Aparte de este caso particular, en repetidas ocasiones se ha señalado cómo ciertas esculturas del Antiguo Egipto tienen un aspecto muy extraño, que recuerda inexorablemente el de partes de mecanismos que, por alguna razón, han sido sacralizadas o de cualquier modo valorizadas estéticamente por medio de la escultura. Especialmente famosa es una pieza que está en el museo de El Cairo que, además de poner de relieve la capacidad habitual del procesamiento de la piedra que llega a niveles increíbles y absolutamente inigualables en comparación de la modernidad, revela también algunas similitudes indudables con algún tipo de hélice. Podemos ver esta obra junto a otras dos, no tan famosas, pero muy significativas, en las fotos de abajo

Ahora, si tenemos en cuenta lo que hemos visto hasta ahora, la idea de una sacralización de partes de mecanismos derivados de una ciencia estimada a su vez como sagrada y utilizada de forma sistemática o incluso única para fines sagrados ya no nos aparecerá tan incongruente. Por lo tanto no nos aparecerá incongruente ni siquiera pensar que Leedskalnin puede haber encontrado una manera de levantar pesados bloques de piedra con técnicas antiguas que él mismo había redescubierto, tal vez de manera casual. Por supuesto, esa hipótesis es menos absurda y increíble que la actitud de aquellos que insisten en creer y repetir que Coral Castle fue construido con los limitadísimos equipos de levantamiento que se encontraron allí o, sólo para referirse a un hecho, que la cuarcita – que es capaz de resistir a las herramientas de diamante más avanzadas que tenemos hoy – había sido perforada por los antiguos egipcios con la sencilla ayuda de puntas tubulares de cobre, arena y mucho sudor.

3) En ocasiones en textos relacionados con la cultura académica se puede leer que los antiguos Egipcios, al igual que otros pueblos del pasado, extraían la piedra mediante la perforación de la roca viva y la inserción de cuñas de madera empapadas de agua, creando así una presión capaz de dividirla. De hecho, eso es lo que podemos ver en la siguiente imagen, que representa una piedra que, por alguna razón desconocida, fue abandonada en la cantera de Asuán, junto a otras imágenes que dan testimonio de operaciones similares, pero llevadas a término.

 

Por tanto, esta hipótesis no es sólo razonable, sino también empíricamente basada en las observaciones de estos restos y de muchos otros de la misma clase, en que se ha mantenido una huella indudable de este tipo de trabajo. Pero hay una cuestión a la que la egiptología académica persiste en no querer contestar, que es la siguiente: ¿ cómo es que se puede perforar el granito rosa de la manera que vemos en las imágenes si se tiene a disposición sólo cobre, arena y mucho sudor? ¿ quién puede tomar en serio una tal mentira sesquipedal si no los que no saben nada de nada del trabajo de la piedra o quien quiera aún menos revisar sus prejuicios evolucionistas sobre la naturaleza de la que llamamos con cierta altanería “Edad de la Piedra”? Decimos esto porque, como hemos dicho pero es bueno repetir, a partir de un gran número de restos arqueológicos esparcidos en todo el mundo debemos inevitablemente llegar a la conclusión de que la Edad de la Piedra fue cualquier cosa menos que una era de atraso técnico y científico y mucho menos de proximidad al estado animal. Personas que han tenido éxito en una operación como la que está mostrada en la imagen no se parecían de alguna manera a monos o, en cualquier caso, no más de esos historiadores y arqueólogos académicos que frente a este tipo de proezas técnicas – o también otras que parecen inconmensurables en comparación con la capacidad actual – siguen repitiendo desde más de un siglo la fábula de la disponibilidad ilimitada de tiempo y de mano de obra, que incluso en el período en que se inventó no era mucho más creíble y científicamente sólida que la de la cigüeña. Estas personas no parecen darse cuenta de que hay “argumentos” que son un verdadero insulto a la inteligencia, a los que puede prestar oído sólo quien no tiene familiaridad no digamos con la técnica del trabajo de la piedra, sino también con los problemas relacionados con el desplazamiento de cargas superiores a la de un coche de gran cilindrada. Sólo para dar un ejemplo: pensamos en la famosa “Piedra de la Luna” de Baalbek, un monolito gigante de 1000 toneladas, impresionante solamente en verlo y que podemos observar en la imagen siguiente

En el estado actual de nuestra técnica no podríamos pensar de ser capaces de desplazar un coloso de este tipo y colocarlo en otro lugar si no construyendo una gigantesca grúa, con doble o triple puente sobre vías, y por lo tanto transformando Baalbek en un gran complejo industrial, poniendo a punto en el ínterin campanas neumáticas con dimensiones y características que hoy en día no existen, excepto como mera posibilidad (muy) teórica. Esto es porque, al tener que colocar las piedras a una distancia menor que el diámetro de un cabello la una de la otra, sería totalmente imposible si se usan las eslingas normales. Todas estas operaciones, por supuesto, deberían estar precedidas de un estudio geológico exhaustivo del suelo y el subsuelo y de eventuales trabajos de consolidación del suelo, debido a que las operaciones de transporte de este tipo pueden crear abismos donde menos se esperan. Sin embargo, en Baalbek no se encuentra nada que pudiera incluso vagamente hacer suponer que para mover esta piedra y otras similares en tamaño y peso (dos fueron colocadas en la base del templo de Júpiter y pesan sólo 200 toneladas menos) se han hecho intervenciones de este tipo. Así que ¿ cómo es que esa piedra ha sido extraída y transportada hasta allí si no con la ayuda de una técnica “otra” que, basándose en fuentes de energía y herramientas que aún no se conocen, fue capaz de obtener los resultados que a partir de la situación actual de nuestros conocimientos aparecen absolutamente impensables?

4) Si de Baalbek pasamos a Alatri, nos damos cuenta de que, observando con una lente x 10 los encajes en los puntos que están todavía intactos a penas se puede ver una delgada línea que separa las piedras poligonales (que pueden llegar a tener incluso quince lados, aunque en general son “sólo” 8-10). A pesar de eso, es posible observar que la línea de conexión es discontinua y en algunos puntos casi increíblemente accidentada, como se puede ver en la imagen siguiente. Así que ni siquiera es posible suponer que para elaborar el encaje se han utilizado unas máquinas semejantes a la fresa y la rectificadora, que hoy en día se utilizan, respectivamente, para obras de alta y muy alta precisión (pero en materiales que casi siempre son metales) para obtener superficies planas o cilíndricas junto a un grado de precisión similar a la de Alatri (que parece estar alrededor de una centésima-milésima parte de un milímetro, incluso si en unos puntos aparece – increíblemente – aún más bajo).

Sin embargo, como se puede ver lo suficientemente bien en la foto, incluso siguiendo líneas tan complicadas, la precisión de la conexión sigue siendo la misma que se encuentra donde aparece más regular. Además, siempre en Alatri, podemos observar muchos puntos del cinturón donde, muy claramente, se ve que la piedra superior “invade” en la parte inferior, como si de algún modo misterioso se hubiera emparentada con ella. Aquí mostramos el ejemplo más evidente en la foto siguiente. Pero el lector curioso puede consultar You Tube y ver videos de Alatri de Gabriele Venturi, y de esta manera va a descubrir muchos otros (y aún otros puede encontrar si visita Alatri y personalmente echa un vistazo; es cosa muy útil porque, entre otras cosas, nunca como en estos casos vale lo que dice el refrán “ver para creer”)

Es difícil simplemente por medio de una foto transmitir el trabajo de observación hecho directamente en un lugar. Pero, de todos modos, incluso de esta manera se puede ver claramente que en el punto indicado por la flecha roja no se puede notar ninguna línea de unión entre la piedra superior y la inferior. Éste y muchos otros puntos de las murallas por lo tanto hacen inclinar hacia una hipótesis que a partir de nuestra química es, por lo menos por el momento, totalmente impensable. Es decir, que las piedras de Alatri se han colocado en un estado pastoso (o líquido) y que la pasta de las piedras superiores, mientras se moldeaba en la forma de las inferiores, al estar en un estado químicamente activo, ha logrado disolver la piedra inferior, tal vez aún no totalmente solidificada, y emparentarse con ella. Si miramos bien, no hay otra explicación posible de los encajes que se encuentran en Alatri si no un química antes de la química, porque ni siquiera el maestro de los maestros albañiles en un centenar de años de trabajo podría producir un solo acoplamiento a “M” como lo que hemos visto en la primera imagen. Tampoco existe, por lo que sabemos, ninguna posibilidad de que dos piedras puedan emparentarse entre sí sólo por estar encajadas entre sí (de hecho, el tiempo produce inexorablemente el efecto de corroer la piedra justo a partir de las conexiones, que, aunque bien hechas, obviamente son los puntos más vulnerables de las murallas, como de hecho se constata en Alatri).

5) Pero, volvamos al punto de interés de nuestro análisis, es decir el mundo del Antiguo Egipto. Para dar al lector una idea de lo absurdo y del infantilismo científico de la “teoría” de la disponibilidad ilimitada de tiempo y de mano de obra hay sólo que pensar que los antiguos Egipcios a lo largo de su historia (y en esto están de acuerdo también los historiadores y arqueólogos académicos indicados arriba) excavaron en la roca viva un número indefinido de kilómetros de túneles subterráneos, en ciertos casos de tamaño muy considerable, y extrajeron y colocaron muchos millones de bloques de piedra caliza para la construcción de edificios de vario tipo (se calculan diez millones sólo para la Pirámides de Guiza y Dahshur, que la egiptología oficial – con el aire de alguien que habla en serio y sin temor a mentís – dice que se construyeron en menos de un siglo: es decir, cien mil bloques al año, uno cada dos minutos y medio, considerando doce horas de trabajo al día, incluyendo los días festivos (que en aquel tiempo eran muchísimos)). El peso medio de estos bloques parece ser alrededor de 4-6 toneladas (un valor meramente indicativo, ya que los cálculos de este tipo son difíciles), pero muchos de ellos, como por ejemplo los de los Templos en Valle de Guiza, llegan al peso de varios cientos de toneladas. Además, en muchos casos la calidad de la piedra caliza es tan alta que su extracción y tratamiento no tenían que ser mucho más fáciles que la extracción y tratamiento de miles y miles de bloques de granito con que se construyeron templos o revestimientos de templos, columnas y estatuas que a veces alcanzan tamaños realmente impresionantes. Un par de ellas, los colosos de Memnon, ahora muy corroídas, se cree que llegaron originalmente incluso a las 700 toneladas cada una. Para dar al lector una idea de estos monumentos, los mostramos en la imagen de abajo

Teniendo en cuenta que las estatuas representan a un personaje sentado, tuvo que haber una gran cantidad de material de desecho, por lo que el bloque del cual se tallaron tuvo que pesar alrededor de 1000 toneladas. Además, los antiguos Egipcios hicieron estelas, tumbas y cámaras sepulcrales de dimensiones a veces muy considerables y, sobre todo, obeliscos que, también ellos, podían pesar cientos de toneladas. Es famoso el obelisco, abandonado sin terminar en la cantera de Aswan por razones poco claras, un gigante aún casi intacto, cuyas dimensiones son aún más inconcebibles que las de la Piedra de la Luna en Baalbek (una vez terminado, se estima que debía alcanzar un peso de alrededor 1400 toneladas). Pero hay casos en los que sobre estas piedras sabemos algo más que su enorme peso o la asombrosa habilidad técnica con que fueron tratadas. No parece que se puede comprender a fondo este hecho, ya que una cuidadosa observación de las incisiones da la impresión de que estas personas eran capaces de incidir el granito con la misma facilidad con que nosotros grabamos materiales relativamente tiernos con máquinas computadorizadas de alta precisión (y, cabe señalar, en dimensiones que son realmente muy pequeñas en comparación con las de los obeliscos de los antiguos Egipcios). Por ejemplo, hay evidencia escrita que los dos obeliscos de Hatshetsup (¡ 600 toneladas cada uno!) fueron extraídos, esculpidos y colocados en siete meses. Sin embargo, en el mundo académico, si alguien pregunta cómo fue posible una empresa tan enorme, la respuesta es sin duda el cuento habitual del tiempo y la mano de obra ilimitados. Un cuento que, en este caso, además de estar en contra de cualquier tipo de evidencia histórico-arqueológica (siete meses no son un tiempo ilimitado) entra en conflicto también con las percepciones más elementales del sentido común. A esto se reducen la ciencia y el método empírico cuando en lugar de su utilización para conocer la realidad son utilizados para defender un sistema de prejuicios, cuya única función parece la de tranquilizar psicológicamente a las personas que por alguna razón necesitan de sentirse a la vanguardia de una supuesta “evolución del hombre”, que, admitiendo que hubo realmente, es cierto que ha tenido unas connotaciones que no tienen nada que ver con las pronosticadas por Darwin y sus sucesores.

6) Pero si usamos la ciencia y el método empírico para entender realmente estos restos, la conclusión es inevitable: si en la Edad de la Piedra los hombres fueron capaces de diseñar y producir obras tan colosales y con características metrológicas que parecen casi no humanas, sus constructores necesariamente tenían que estar en posesión de una ciencia y por lo tanto de una técnica y fuentes de energía que podían ponerlos en condiciones de alcanzar sus objetivos. De lo contrario, tenemos que imaginar que no eran hombres, sino los míticos Titanos a los cuales los Griegos clásicos atribuían sin dudar las murallas de Micenas. Es cierto, sin embargo, que las características exteriores de esta ciencia y técnica parecen ser muy distintas de las que toman en nuestro mundo. Y esto sin duda ha contribuido al hecho de que hasta ahora sólo una minoría de los investigadores ha sido capaz de reconocerlas. Por otro lado, no es de extrañar mucho: como un libro de aritmética escrito en antiguos caracteres chinos no parecería a ningún occidental un libro de aritmética (a parte los que conocen bien el chino antiguo), así también la forma de utilizar la alta geometría que hemos descubierta como típica de los relieves de los antiguos Egipcios se equivocó con un bosquejo primitivo del arte figurativo. Nadie se dio cuenta de lo que realmente se trataba, es decir una manera sorprendente de codificar al mismo tiempo ideas teológicas, datos astronómicos y teorías científicas a través de figuras construidas por medio de un sistema de derivadas logarítmicas. Sin embargo es bastante comprensible que se haya producido una equivocación de este tipo, dado que a ningún occidental moderno se le ocurriría de construir imágenes de acuerdo con ese sistema (en nuestra cultura el arte figurativo se ha siempre considerado arte imitativo) o incluso que las matemáticas y astronomía pueden tener algo que ver con la religión. Aparte de eso, para la mentalidad moderna es muy problemático, por no decir totalmente increíble, la idea de que un poder técnico-científico capaz de diseñar y construir un paisaje sagrado monumental como el de Guiza y Dahshur se haya sido aplicado de forma prácticamente exclusiva al arte sagrado. Bien mirado, gente como los antiguos Egipcios, que eran capaces de mover con relativa facilidad millones de bloques de piedra caliza que pesan varias toneladas, después de las invasiones extranjeras del Este, habrían podido transformar su nación en un sistema de fortalezas inexpugnables, en condición de hacer frente a cualquier posible invasor (recordemos que sólo con la piedras de la Gran Pirámide se podrían construir todas las catedrales de Europa occidental o toda la ciudad de Londres: ¿ qué habrían podido hacer los Persas, los Macedonios o incluso los Romanos contra una cadena de fortificaciones de este alcance?). Y, sin embargo, contra toda expectativa, esta gente utilizó su conocimiento y poder sólo para honrar a sus dioses y con respecto a la guerra no se tomó la molestia de utilizar más que las herramientas de la Edad del Cobre antes y del Bronce después.

7) A nuestra mentalidad esta actitud aparece realmente enigmática y sin duda habrá alguien que la considera supersticiosa o incluso estúpida, semejante a aquella para la que los Chinos usaron la pólvora sólo para los fuegos artificiales sin darse cuenta de sus posibles aplicaciones civiles y, sobre todo, bélicas (que en cambio en Occidente se entendieron y utilizaron de inmediato, entre otras cosas para someter el imperio chino a su propia voluntad y a sus propios intereses comerciales). La idea de progreso y la de “utilidad” están tan arraigadas en nuestra mente que es muy difícil para nosotros imaginar que en el mundo ha habido (y hay) personas que ven la vida de tal forma que miran con sospecha cualquier tipo de innovación, que no tienen duda sobre el hecho de que la ciencia y la tecnología son algo sacramentalmente conectado con la religión y por lo tanto con el arte religioso y la arquitectura sagrada, y que por eso consideran algo así como una blasfemia su aplicación a otros fines (suponiendo que a alguien se le ocurra de hacerlo: porque, al menos mirando el Antiguo Egipto, no parece posible encontrar ninguna aplicación “útil” de esa técnica misteriosa utilizada para construir los monumentos religiosos). Sin embargo, al parecer, esto que para nosotros es absurdo, en otros tiempos y en otras culturas era una regla de vida tan obvia que tal vez nadie se ha nunca plantado la cuestión de aceptarla o no. Un poco como es para nosotros la idea de que tanto más desarrollado es un país cuanto mayor es su producto interno bruto; y a nadie o casi a nadie le importa si este mundo y lirondo dato económico –¬ que muy poco tiene que ver con la felicidad de los seres humanos – implica la destrucción sistemática y a veces irreparable del ambiente en que vivimos o terribles conflictos para apoderarse de las materias primas para producir objetos de dudosa utilidad o completamente inútiles (sólo para dar un ejemplo, en Congo, un país tanto lejos de las crónicas cuanto rico en materias primas, la guerra de diversas maneras ha matado a diez millones de personas de una población total de setenta, sin que nadie en nuestros países tenga la menor duda de la utilidad del producto interno bruto). Tenemos pruebas que en tiempos muy antiguos, incluso en pleno Paleolítico, una cosa así ha ocurrido en Dolni Vestonice, donde se encontraron dos hornos para cocer cerámica a altas temperaturas que se remontan a 28.000 años a. C. y pensar que hasta el momento de este descubrimiento realmente sensacional se creía que la cerámica había sido inventada en 10.000 a. C. en conexión con la agricultura. A pesar de toda expectativa razonable, se ha visto que esta técnica refinada y, diríamos, útil para una multitud de fines prácticos, al parecer nunca se ha utilizado más que para producir imágenes de mujer o, de todos modos, esculturas de los que parecen objetos de culto, que después eran quebrados ritualmente. Ni una vasija ni una jarra ni un plato ni un utensilio de cualquier tipo: ¿ cómo es posible que gente capaz de dominar una técnica tan compleja no la utilizaría también para algún tipo de finalidad más práctica? Eso es algo inconcebible para la mentalidad moderna, ya que estamos acostumbrados a considerar la ciencia y la religión como dos campos separados, donde la ciencia es dedicada esencialmente a aumentar el poder del ser humano sobre la naturaleza y los otros seres humanos. Por cierto, ninguna de las potencias mundiales actuales se imaginaría de reservar la energía atómica a la adoración de una divinidad y descuidar sus aplicaciones, bélicas o civiles. Probablemente es justo esta peculiaridad de nuestra situación cultural la causa profunda de aquel endurecimiento de nuestra capacidad de interpretación histórica – que se parece a una verdadera barrera psicológica – que nos impide tan sólo imaginar que las matemáticas pueden tener un papel diferente en la vida humana de aquel que de hecho tienen actualmente en nuestro mundo. Desde la secundaria hemos estado acostumbrados a pensar que la ciencia empírica se ha desarrollado en Occidente y no en otras partes, porque sólo en Occidente hubo aquella división entre lo sagrado y lo profano que nos ha permitido investigar en áreas donde siempre en otras partes reinaron no contrastados el mito y el dogma religioso. Pero – suponiendo que esto es cierto – sin duda hay una forma diferente de pensar acerca de la ciencia, y para entenderlo es suficiente ir al fondo de las consideraciones que hemos hecho un poco arriba cuanto a la posibilidad de construir las constantes de las leyes científicas por medio de π y ϕ.

QUINTA PARTE: LOS POSIBLES FUNDAMENTOS TEOLÓGICOS Y ASTRONÓMICOS DE LA CIENCIA PREHISTÓRICA

1) Para avanzar en esta investigación tal vez la mejor manera sea la de empezar con el ejemplo que en este contexto parece el más interesante, a saber el de la fuerza electromagnética activa entre dos electrones, que se expresa por una constante α igual a 1/137,036. Parece que el gran físico Paul Dirac estaba muy intrigado por esa peculiaridad de la constante (es decir que era prácticamente idéntica a 1/137.mo) y que en el tema contaba esta historia: un hombre que llega en el Paraíso puede hacer a Dios una sola cuestión y entonces le pregunta: “ ¿ por qué justo el 137?”. En base a lo que hemos descubierto hasta ahora podemos plantear una hipótesis de respuesta. Aunque no sabemos si ella podría satisfacer en todos los aspectos a este famoso físico, que era muy exigente en términos de exactitud matemática. Como hemos visto de manera más profunda y detallada en la cuarta parte de este trabajo (The Snefru Code, part. 4: “El número de oro en el arte y arquitectura sagrados del Antiguo Egipto: una perspectiva archeoastronómica”), teniendo idealmente inmóvil y por lo tanto tomando como punto de referencia el plano ecuatorial en un momento típico del ciclo solar – digamos – en el solsticio de verano, podemos considerar el eje polar de la tierra como una especie de manecilla que en el curso de un ciclo de precesión oscila de ± 47° respecto a la eclíptica. Así, al final de un semiciclo de oscilación hay que añadir a los 90° de inclinación del eje polar con respecto al plano ecuatorial los aproximadamente 47° de los cuales esta manecilla cósmica se mueve en los aproximadamente 13.000 años que dura la mitad de un ciclo de precesión. De este modo se pasa de la sección de 90° + 270° = 360° del solsticio de verano que tomamos como punto de referencia a 90° + 47 = 137° + 223° = 360°, cuando ese mismo punto de la órbita, después de 13.000 años de oscilación, se ha transformado en un solsticio de invierno. En la imagen de abajo podemos tener una clara idea visual del fenómeno

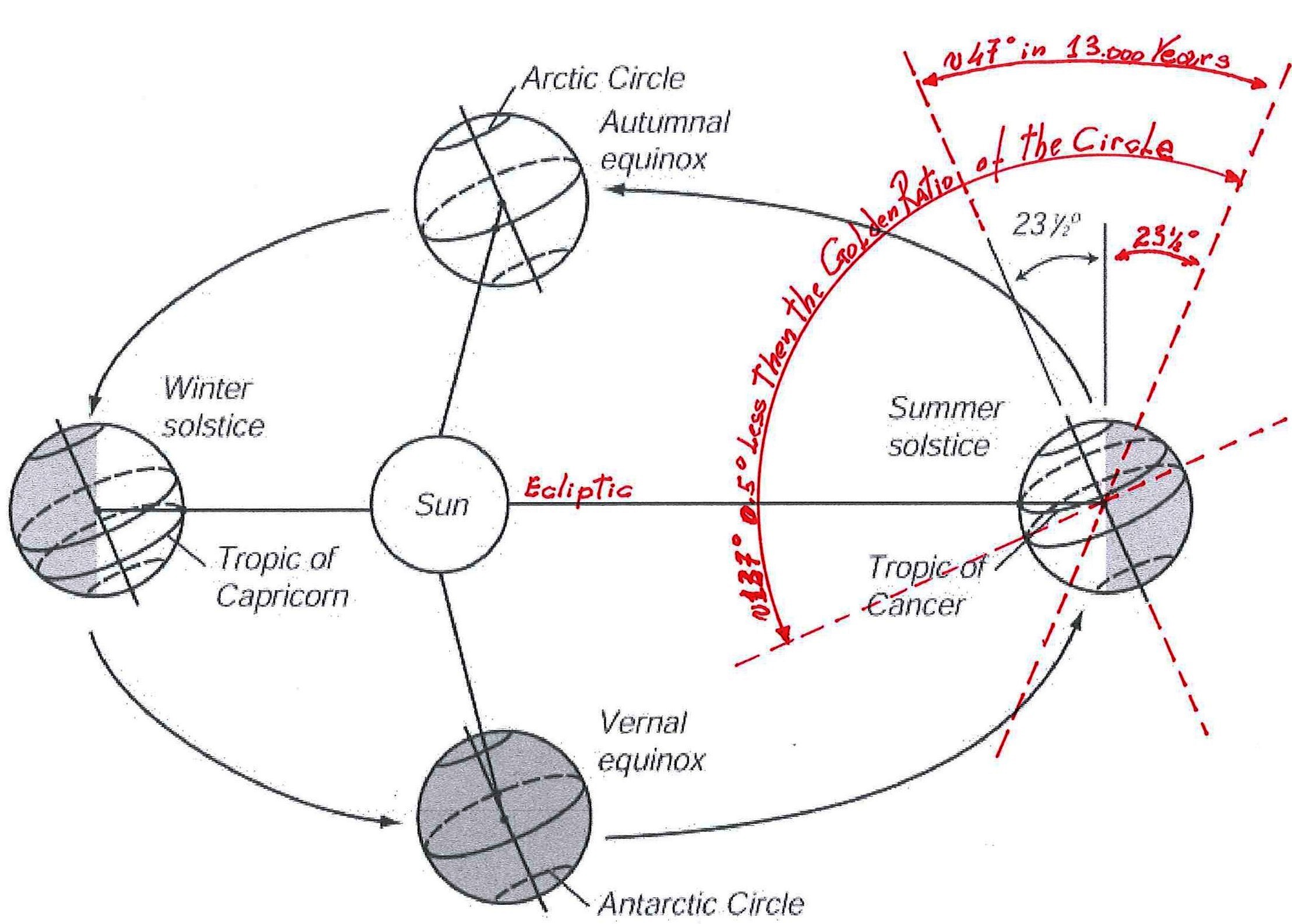
Se trata – por razones de conveniencia – de una imagen derivada de nuestra forma habitual de representar el cosmos, aunque, como hemos visto en la segunda parte de este trabajo, lo que en un cierto sentido podemos sin duda definir un hecho científico parece ciertamente contenido en los relieves del Antiguo Egipto, aun cuando está representado de una manera para nosotros muy inusual y, sobre todo, en un contexto de misterio religioso. Sin embargo, hay que señalar que en este tiempo la tierra oscila entre una sección de 270°/90° y una muy cerca de la sección áurea del círculo, que resulta de 360/ϕ = 222,49°, con un ángulo recíproco igual a 360 – 222,49 = 137,51 (la diferencia es aproximadamente de medio grado). Obviamente, podemos decir que una oscilación similar ocurre cada seis meses entre los dos solsticios opuestos, aunque de manera diferente, ya que el mismo punto de la tierra está inclinado de ± 47° con respecto a la eclíptica. Ahora bien, esta situación astronómica, al menos en términos de numerología, parece tener algo que ver con la fuerza electromagnética activa entre dos electrones, debido a que en las dos situaciones aparece como elemento decisivo el mismo número, el 137. En efecto, como hemos visto anteriormente, esta forma se expresa por una constante igual a 1/137,036. Así que, quién sabe, tal vez en la historia de Dirac a este hombre que le pide a Dios “¿ por qué el 137?”, Dios podría contestar que eligió el 137 porque este número corresponde al recíproco de la “casi” sección áurea sobre la que la tierra oscila durante cada año solar o de precesión.

2) De hecho, 1/137,036 = 0,007297352…, que – ¡ por casualidad! – multiplicado por el ángulo completo (es decir 360) da 2,627, un número más o menos igual a ϕ². Si realizamos la raíz, tenemos 1,6208…, es decir un número un poco más de 2/1000 mayor del número de oro. Esto significa que podemos llegar a expresar un valor muy similar al de α con la expresión ϕ²/360, que es igual a 0,0072723. En este contexto vale la pena recordar que 360, además de los grados del ángulo completo, son también los días “normales” del calendario solar del Antiguo Egipto y de los Maya. ¿No podría esto ser el indicio de que estos importantes conceptos científicos, además de los monumentos, pueden haber sido codificados por la sabiduría del pasado incluso en objetos para nosotros tan inocuos y triviales como los antiguos calendarios y sus números típicos tan inusuales desde nuestro punto de vista? Más adelante veremos también otras formas en que una manera de pensar acerca de la ciencia tan extraña para nosotros puede haberse originado en el espíritu de personas que tenían una actitud muy diferente de la nuestra con respecto a la vida y el cosmos. Por el momento, queremos subrayar que hay una conexión adicional entre el ciclo de precesión y el número de oro (y, por lo tanto, hablando de una forma numerológica, con la constante α). Una conexión, que tal vez para nosotros puede ser una mera curiosidad, pero para gente acostumbrada a pensar en la ciencia y las matemáticas de manera diferente, pudo haber sido una indicación de las huellas dejadas por la mente divina en el momento de generar el mundo. De hecho, la raíz cuadrada de 26.000 años de un ciclo de precesión dividida por 100 es igual a 1,61245…, es decir a un número que difiere del número de oro de menos de 5 milésimos (también el ciclo de Sirio contiene conexiones similares con el número de oro: los 1461 años de su duración, multiplicados por ϕ³, dan una cifra igual a 6188,89, que es más o menos igual a 1/ϕ x 10.000). Estos hechos tienen, por supuesto, unas consecuencias muy significativas en cuanto a las relaciones numerológicas del ciclo de precesión con las constantes científicas o las que se pueden establecer entre las mismas constantes científicas. Como ya hemos visto y como veremos aún mejor más adelante, ya que estos números muy importantes parecen ser capaces de traducirse – al igual que los ciclos cósmicos – en funciones de π y ϕ, también tienen entre ellos una relaciones que pueden parecer – se diría – extrañas. Por ejemplo, si dividimos ħ por α, vemos que ħ/α = 1,054571:0,0072992… = 144,476326462. Este número es casi idéntico a 26.000:360 x 2 = 144,444…, un número que corresponde a los que vamos a conocer como dos Días de Precesión (veremos en breve lo que es). O bien, si multiplicamos la constante de la cual se obtiene “c” (“c” es la velocidad de la luz) por α y después realizamos quatro veces la raíz, vemos que √(√(√(√(2,9979246 x 0,0072992) = 0,62017…, es decir un número más o menos igual a 1/ϕ, con una diferencia de poco más de 2 milésimos. Si en cambio dividimos la constante gravitacional G por α y realizamos la raíz octava, vemos que √(√(√(√(√(√(√(√(G/α) = √(√(√(√(√(√(√(√ (6,67 : 0,0072992) = √(√(√(√(√(√(√(√913,79877… = 1,05470…,, es decir un valor que es diferente de ħ de un poco más de 12 diez milésimos. Encontramos un valor incluso más aproximado a ħ si dividimos por ϕ los 1461 años de duración de un ciclo de Sirio y si realizamos una vez más la raíz octava: √(√(√(√(√(√(√(√(1461/ϕ) = √(√(√(√(√(√(√(√902,9476 = 1,054608, en comparación con los 1,054571 de nuestra constante. Por último, podemos relevar que, ya que un electronvoltio es 1,60217653 x 10‾19 J, sin ninguna ecuación particular observamos que la diferencia entre la aproximación al número de oro que resulta del ciclo de precesión (1,61245) y esta constante es poco más que un centésimo. Tal vez ni siquiera es un caso que la aproximación al número de oro que en cambio se deriva de la Pirámide de Micerino es 1,601, con una diferencia con respecto al valor de un electronvoltio aproximadamente de un milésimo.

3) Sobre la base de estos datos y teniendo en cuenta la relación entre la religión, la astronomía y el profundo conocimiento que se tenía incluso en tiempos muy antiguos del fenómeno de le precesión, ahora nos podemos preguntar: ¿ por qué seres humanos con una orientación espiritual muy diferente de la nuestra no podrían ser llegados a conocer la constante α tal como la conocemos nosotros y al mismo tiempo, al ver que es asociada o asociable con el ciclo de precesión y con otras constantes físicas por medio de π y ϕ, no podrían haber visto en eso las huellas de una armonía divina en lugar de una mera casualidad? Pensemos en esto: ¿estamos realmente obligados por la ciencia o incluso por la lógica a creer que todos estos datos científicos y matemáticos que hemos visto codificados en obras del Antiguo Egipto son sólo una trivial acumulación de coincidencias? Observando los monumentos que nos han quedado, en particular la precisión y, a veces, la singularidad de su orientación astronómica, hay que concluir que esta gente parecía realmente convencida de la conexión básica entre astronomía, matemáticas y teología, algo que en nuestros tiempos y en nuestros lugares es considerado como una especie de ingenuidad epistemológica intolerable, una superstición incluso más perjudicial que inútil. Pero, mirando a los resultados obtenidos por nuestros antepasados, por ejemplo en la arquitectura, ¿ podemos estar de veras científicamente seguros o demonstrar lógicamente que es cosa de primitivos atribuir las leyes que operan en el cosmos a Dios o a los dioses más que a la casualidad (sea lo que sea)? Y si no podemos estar seguros, ¿ por qué deberíamos excluir que en el lejano pasado de la humanidad puede haber existido una cultura o un conjunto de culturas que vieron en la teoría de la relatividad y la mecánica cuántica una huella de la inteligencia divina, si una persona como Einstein no exitó en verla? Más arriba hemos constatado que las constantes de nuestras leyes físicas más fundamentales pueden ser derivadas – aunque con alguna aproximación – de π y ϕ, que a su vez son más o menos crípticamente codificados en fenómenos y por lo tanto en todo tipo de ámbitos del conocimiento. Conscientes de todas estas conexiones, ¿ estamos realmente obligados a juzgar a los que consideran la ciencia desde una perspectiva diferente de la positivista-materialista como ingenuos o incluso supersticiosos? Sin querer forzar una opinión de una manera u otra y manteniendo una posición de firme relativismo cultural, podemos relevar que incluso el intelectual más laico del mundo se habrá dado cuenta de que la noción de “lenguaje” y de “signo lingüístico” parece profundamente conectada con la de “regularidad”, ya que el significado de un signo es dado – entre otras cosas – también por su inexorable repetición dentro de ciertos contextos, es decir, como diría Ludwig Wittgenstein, por la constancia de algunas de sus aplicaciones, que podemos definir típicas. Así que no sería demasiado sorprendente que personas con tendencias espirituales diferentes de las de la mayoría de nuestro tiempo hayan visto en las regularidades matemático-cuantitativas descritas por las leyes científicas – unidas a las de la “numerología”, que nosotros consideramos como meras supersticiones – una forma en la que lo divino se comunica con el hombre a través de símbolos matemáticos. La regularidad con la que π y ϕ aparecen en las constantes de las leyes científicas y en los ciclos cósmicos (vamos a analizar más profundamente estos hechos en los últimos párrafos y advertimos al lector de que realmente se asombrará) puede de veras parecer una manera con la cual un “dios agrimensor” o “matemático” comunica secretos al ser humano que contempla el universo. En tal contexto, nadie podría sorprenderse que los números pueden haber sido considerados como sagrados, y que por lo tanto en la antigüedad la ciencia haya buscado no sólo y no tanto un mero poder de cálculo y manipulación de la realidad, sino una divina armonía, revelada por unos números que fueran Ley de todas las leyes.

4) Una huella de esta actitud se puede encontrar a partir una vez más de algunas observaciones sobre el ciclo de precesión, cuyos números básicos parecen tener una relación tanto escondida cuanto profunda y sugestiva tanto con unos calendarios muy antiguos como con el sistema geométrico todavía en uso en Occidente que todos sabemos que deriva directamente del babilónico. Por lo que sabemos, durante el ciclo de precesión el eje del polo terrestre con respecto al polo celeste oscila entre un mínimo de aproximadamente 21,5 y un máximo de 23,5 grados. Esto hace que el ángulo total entre los dos solsticios opuestos en el primer caso sea 43° y en el segundo 47°. A parte del hecho curioso de que la suma de estos dos ángulos es igual a 90° y la media a 45° – es decir igual a un cuarto y a un octavo del ángulo completo como es calculado en el sistema trigonométrico babilónico – hay que añadir también otro, que es quizás aún más sorprendente (y que probablemente está relacionado con éste no sólo matemáticamente sino también históricamente). De hecho, si tratamos de construir la tríada pitagórica (que corresponde a un triángulo rectángulo con los tres lados constituidos por números enteros), usando como base el 47 y el 43, vemos que el cateto menor es justo igual a 360 (el otro lado es 4042, mientras que la hipotenusa es 4058). Se trata – ¡casualidad! – de esas 360 partes en las que en la antigüedad era dividido el ciclo de precesión (que en este contexto podemos simplemente definir Año de Precesión) para encontrar la duración de un Día de Precesión, que resulta de 26.000 : 360 = 72,222 años (que multiplicados por dos, como hemos visto anteriormente, dan un mínimo prácticamente idéntico a ħ/α). Este hecho matemático indudable nos da una razón teológico-astronómica capaz de arrojar luz sobre el motivo por qué los Babilonios utilizaban el sistema sexagesimal en un giro calculado en 360 grados: esto ocurría porque, con toda probabilidad, el círculo al que se referían era el de la precesión no el del año solar. Por tanto la orientación de un zigurat, como el que vemos abajo, podría tener unos significados que van mucho más allá del año solar. Y así se observan extrañas coincidencias y congruencias con la disposición de las grandes Pirámides de Abusir

También los ángulos que vemos en la estructura que se muestra en la imagen siguiente podrían tener unos significados asociados con la precesión, y por lo tanto merecen un breve análisis

Como hemos visto, el ángulo de 45° podría simbolizar la media del ángulo que resulta entre los dos opuestos solsticios cuando el eje polar está inclinado al mínimo y al máximo respeto a la eclíptica; pero también a la derecha podemos encontrar un ángulo muy interesante. De hecho, si dividimos este nuevo triángulo en dos triángulos rectángulos – como lo hicimos en la imagen – vemos que el de derecha tiene los ángulos típicos de aquél construido en la mitad del lado y en la altura de la Gran Pirámide (con todas las consecuencias con referencia a π y ϕ, que han sido abundantemente demostradas con respecto a la Gran Pirámide); pero también los ángulos opuestos a los catetos de el de izquierda (que son aproximadamente de 48° y 42°) muestran unas características notables. Por ejemplo, la relación 48/42 es igual a 1 + 1/7, mientras el ángulo recto tiene con el ángulo menor una relación igual a 2 + 1/7. Son números que podrían indicar cierta relación de la estructura con el ciclo lunar, en particular con la semana, una unidad de medida que aún es familiar a todos. Hay que tener en cuenta que la raíz cúbica de un séptimo es igual a ³√ 0,142857… = 0,614788, es decir un número que difiere de 1/ϕ de poco más de tres milésimos (cosa que podría haber llevado a los antiguos matemáticos a conectar la semana lunar y por lo tanto la Luna con el número de oro). Si a continuación intentamos construir la tríada pitagórica también con el 48 y el 42, vemos que una vez más salen características notables y, es de imaginar, en ningún modo casuales. De hecho, el perímetro del triángulo rectángulo conexo es igual a 8640, el cual, dividido por el ángulo completo (es decir 360) da 24. O, dividido por 540 (que es la medida de su cateto menor, y por lo tanto puede ser escrito como 360 + 360/2) da 16. Esta estrecha relación de la tríada pitagórica con el 360, en una cultura en la cual el círculo era dividido justo en 360 partes, parece una alusión a alguna noción exotérica de tipo astronómico, cuya naturaleza en este momento no es fácil reconstruir, pero con un poco de paciencia podremos ser capaces de descubrir. Por ejemplo, el 16 podría representar un doble ciclo de 8 fases lunares, y el 24 un ciclo triple. Pero, aparte de esto, incluso de lo poco que hemos visto hasta ahora, podemos apostar a que no sólo los detalles que hemos identificado, sino también el conjunto de esta gran estructura tiene sin duda un significado astronómico, con toda probabilidad relacionado de manera hermética con el ciclo de precesión.

5) Pero, si volvemos a la tríada pitagórica y al triángulo rectángulo de los que partimos, los que son numerológicamente asociados con la inclinación máxima y mínima de la tierra con respecto a la eclíptica (23°,5 y 21°,5), nos queda todavía por observar que, aparte de las que parecen obvias conexiones con la trigonometría y, por tanto, con la arquitectura babilónica, desde el punto de vista arqueoastronómico-numerológico hay también otras características muy interesantes, que nos pueden dar inspiraciones importantes para la comprensión de la estructura del pensamiento de otras culturas antiguas. En primer lugar, observamos que el perímetro del triángulo es 8460, que dividido por 360 nos da 23,5, es decir la inclinación de la tierra con respecto a la eclíptica cuando llega al máximo, o la declinación de la luna cuando alcanza el punto medio entre el máximo y el mínimo. Si hacemos la relación entre el perímetro y el número que resulta de la suma de la hipotenusa con el cateto mayor (excluyendo así el de 360), tenemos un resultado igual a 1,04444…; elevando este número a la undécima potencia, se llega a una cifra igual a 1,613…, que es de solos 5 milésimos inferior al número de oro (y todos sabemos cómo el 11 es un número que en la serie de Fibonacci íntimamente relacionada con el número de oro, juega un papel muy particular). El área del rectángulo construido en los catetos es igual a 1455120. Dividiendo este número por el perímetro del triángulo del que partimos nos encontramos con una relación igual a 172: y sabemos que la luna describe en la esfera celeste un círculo inclinado de 5°,15 con respecto a la eclíptica, un valor que está sujeto a cambiar con la variación en el tiempo. La variación es de tipo periódico, con un periodo de 173,3 días, muy cerca del que hemos encontrado a partir de nuestro triángulo, llamémoslo así, “de precesión”. También – y esto es quizás el lado más sorprendente, los 5°,15 de inclinación del círculo lunar con respecto a la eclíptica corresponden de manera prácticamente exacta al ángulo opuesto al cateto menor de este triángulo. Observamos de pasada que en la tumba de Djehutihotep (que se remonta a la XII Dinastía) se encuentra una imagen de una estatua de alabastro que es tirada en un trineo por 172 trabajadores, que por haber llegado a arrastrar y colocar esta estatua son celebrados como héroes, mientras, bien mirado, la estatua aparece tener dimensiones y peso ligeramente reducidos (alrededor de 60 toneladas) en comparación con estatuas y obeliscos con dimensiones diez veces más grandes que de hecho fueron transportados y colocados más que una vez en el curso de la historia del Antiguo Egipto. Aquí encontramos una razón para pensar que los 172 trabajadores que arrastran el trineo no son seres humanos, sino el símbolo matemático, se diría “humanizado”, del número que sale elaborando esta particular tríada pitagórica, que tal vez se utilizó como símbolo hermético de este ciclo lunar muy importante. Tal vez ni siquiera es un caso que el perímetro de este triángulo, multiplicado por π, nos da un valor de 26577, que es un número bastante cerca de aquel de las unidades de 360 días que son necesarios para medir un ciclo de precesión de 26.000 años solares de 365,25 días (que es, de hecho, 26.379). Por lo tanto, en los ángulos de la inclinación máxima y mínima de la tierra con respecto a la eclíptica parece insertado un conjunto de conceptos astronómicos importantes, que en el ámbito de estos números parecen relacionados dentro de un sistema numerológico del cual se pueden extraer por medio de una elaboración matemática que podemos definir “esotérica” (pero hay que preguntarse cómo esta palabra sonaría en los oídos de personas a las que nos inclinamos a atribuir precisamente una “cultura esotérica”).

6) Probablemente era simplemente justo dejar por último el motivo de interés principal de la tríada pitagórica que resulta del 47 y del 43, o el hecho de que en ella parece también escondida la solución de un enigma que ha ocupado durante largo tiempo a los historiadores y arqueólogos, pero sin ningún fruto. Estamos hablando de por qué tanto en el mundo de los Antiguos Egipcios que en el de los Maya los 5 días que exceden los 360 en el año solar fueron juzgados infaustos. Una maldición parecida podría derivar del hecho de que estos 5 días – en el ámbito de una cultura en que la numerología asumió un papel tan importante – podían ser vistos como motivo de falta de armonía entre el recorrido anual del sol a través del zodiaco y el de la precesión de los equinoccios que el sol hace cada 26.000 años andando en la dirección opuesta el mismo círculo cósmico: algo que en el ambiente cultural de este tipo debía ser percibido como de malos auspicios, un elemento de caos a ser combatido por todos los medios sagrado-simbólicos disponibles. En este sentido, es oportuno recordar que entre los diversos calendarios maya hay un Largo Cómputo que consta de 5200 unidades de 360 días cada una, de las que nadie ha sido capaz de explicar la función, no obstante alguien ya ha señalado que 5 Largos Cómputos, ya que llegan a un total de 26.000 unidades de 360 días cada una, podrían de alguna manera conectarse con el ciclo de precesión. En este punto de nuestra investigación, después de descubrir que la tríada pitagórica que podemos extrapolar del 43 y del 47 tiene exactamente el 360 como término menor, podemos estar prácticamente seguros de que su función era precisamente ésta. Medir el ciclo anual del sol mediante la eliminación de los 5 días que sobran por respecto al número que sale de la tríada pitagórica conexa con los ángulos extremos tocados por la tierra en relación con la eclíptica, era una manera de ajustar los números fundamentales de los ciclos fundamentales. De esta manera el ciclo anual del sol a lo largo del zodiaco (que ocurre en el sentido opuesto al de las agujas del reloj) no vendría numerológicamente y por lo tanto mágicamente en conflicto con el de la precesión (que ocurre en el sentido inverso). Es bastante obvio que este tipo de operaciones es totalmente innatural para cualquier persona que ha crecido en nuestra cultura. Por supuesto, un científico que se pondría la cuestión de introducir un calendario particular porque los números del calendario habitual no se corresponden con determinados ciclos astronómicos – supuesto que alguien le escuche – sería tomado por loco. Sin embargo, estas cosas, al parecer, eran muy, muy importantes en el mundo antiguo, en el que el cálculo del tiempo tenía relaciones muy fundamentales con la religión y, por tanto, con la vida cotidiana de las personas. Se considere que incluso en los tiempos de Roma una de las tareas fundamentales de los sacerdotes era la de encontrar la manera de reconciliar el calendario y, por tanto, el ciclo solar con el ciclo lunar, una tarea muy complicada a la que también otras culturas del pasado se entregaron de varias maneras y que de varias maneras solucionaron.

7) Por supuesto, los argumentos que hemos traído aún parecen insuficientes para establecer conclusiones ciertas 100%; pero realmente parece difícil de explicar la geometría del arte sagrado del Antiguo Egipto y de Babilonia de otra manera que con conocimientos matemáticos y astronómicos muy avanzados, totalmente comparables a los nuestros – y tal vez más avanzados – pero vividos y representados como parte esencial de un misterio religioso. Es por eso que cada vez que los encontramos nos quedamos completamente desconcertados y perplejos, porque nos parece increíble que un estudio de la astronomía casi fanáticamente “exacto” como el de los Babilonios pueda tener que ver con un fenómeno como la religión. Esto se debe a que hoy en día la religión tiene connotaciones totalmente diferentes, que nada tienen que ver con la astronomía y, sobre todo, con las matemáticas o la numerología, ya que también ellas un tiempo eran parte de la tradición teológica – cosa que todavía se puede encontrar fácilmente en un texto como la Apocalipsis o en otras partes de la Biblia – pero por lo general es pasada por alto por los teólogos modernos. Esto significa que cuando vemos imágenes como la siguiente siempre permanecemos perplejos: ¿ qué tienen que ver los dioses y lo divino con un conocimiento tan profundo y “exacto” del cielo diurno y, sobre todo, del cielo nocturno?

De hecho, a partir de restos de este tipo, muchos historiadores y astrónomos se han sentido presionados o incluso forzados a asumir que los Babilonios de alguna manera se habían dado cuenta de la configuración real del sistema solar por lo menos cinco o seis milenios antes que esta conciencia llegara a Occidente. Se considere que un gran astrónomo como Kepler, muy atento observador del cielo, todavía estaba perfectamente convencido de que los planetas eran sólo seis. Una cosa que no es de extrañar, ya que los planetas más periféricos del sistema solar no son fáciles de localizar, incluso si se utilizan las técnicas modernas de cálculo y observación. Sin embargo, entre los Babilonios este conocimiento tan profundo del sistema solar era una parte inseparable de una visión religiosa del mundo, en la que la astronomía matematizada tenía un papel igualmente esencial que el del mito, por el cual era totalmente compenetrada. Una cosa que es totalmente incomprensible en un mundo como el nuestro, donde la religión y las ciencias matematizadas de todo tipo no tienen ninguna forma de relación verdaderamente profunda. Planteando el problema de esta sacralización de las matemáticas y la astronomía matematizada – que evidentemente tuvo lugar en todo el mundo antiguo además que entre los Babilonios – podemos asumir que un factor que puede haber llevado a esta gente a considerar las teorías científicas como parte de los misterios religiosos era justamente la posibilidad de obtener sus números fundamentales – o sea las constantes – de ϕ y/o de π. Es una posibilidad que ya hemos visto y analizado más arriba, pero sólo en mínima parte. Tomando de nuevo estas consideraciones y análisis, podemos ampliarlas con la hipótesis que estas personas no vieron – como nosotros – en π y ϕ unos números casuales o “irracionales” o de todas maneras incomprensibles, sino, por lo contrario, justamente como el summum de la racionalidad y comprensión. Al verlos como un atributo de la mente divina (como los veía todavía Kepler, aunque a oscuras de la posible magnitud de su significado científico), que crea y recrea el cosmos de acuerdo con las leyes que derivan de estos números, conocerlos significaba en un cierto sentido conocer a Dios, cuya infinitud tal vez se sintió de manera totalmente diferente de la nuestra. Para nosotros, lo infinito es en primer lugar un elemento de perspectiva espacial, una lejanía impensable a la que nos acercamos psicológicamente – como claramente muestra Giacomo Leopardi en sus “Canti” y el “Zibaldone” – con la idea y, sobre todo, con el sentimiento de lo indefinido. Pero tal vez estas personas no pensaban así. Tal vez para ellos Dios era algo infinito o transcendente, porque los que podríamos definir sus “números profundos” son inexpresables en el lenguaje y el pensamiento humano, sino de una manera aproximada. Desde este punto de vista, construir las constantes de las leyes científicas por medio de π y de ϕ podía ser un modo de derivarlas, digamos, del poder divino, que a lo mejor se creía que actuaba por medio de estos números.

8) Para hacerse una idea de lo que se puede hacer con π y ϕ, además de los casos muy importantes que hemos visto anteriormente, podemos traer otros, en los que las constantes científicas pueden convertirse en productos de estos números. Por ejemplo, la constante de Boltzmann puede ser expresada con el número de oro por medio de la simple fórmula 1 + (1 – 1/φ) = 1,381966 contra un valor actualmente en uso de 1,380054, con una diferencia de 0,0019, que podría eliminarse casi perfectamente por una corrección obtenida con (1/φ)13, que da un resultado igual a 0,00191… La constante de Stefan-Boltzmann – usando el valor π que hemos encontrado en el sarcófago de Djedefre – puede expresarse por la fórmula (πDjedefre x ϕ) + 1/ϕ = 5,669 contra un valor igual a 5,6697, con una diferencia de 7 diezmilésimos. La carga del electrón (1,60219) difiere de ϕ “en persona” de poco más de 15 milésimos (1,618033 – 1,60219 = 0,01584): mediante la fórmula ϕ – (1/ϕ)9 tenemos 1,618033… – 0,013155… = 1,60487… con una diferencia que se reduce a poco más de 2 milésimos (un poco más arriba vimos que la carga del electrón corresponde casi a la perfección a la aproximación al número de oro que se puede sacar de la Pirámide de Micerino). La permeabilidad magnética del vacío (1,2566) difiere de la raíz cuadrada de ϕ de un valor también muy bajo (1,2566 – √ϕ = 1,2566 – 1,2720 = – 0,0154) y puede ser “arreglada” de la misma manera: √ϕ – (1/ϕ)9 = 1,2720 – 0,013155 = 1,2588, con una diferencia de 22 diezmilésimos. La masa en reposo del electrón se puede calcular usando la fórmula π² – [2 x (1/ϕ)²] = 9,10566, contra un valor actualmente en uso de 9,1091, con una diferencia de menos de 4 milésimos. La constante dieléctrica del vacío es igual a 8,85544; con la fórmula (π x ϕ) + π + 1/ϕ se obtiene un valor de 8,8428, con una diferencia de poco más de un centésimo. La constante de Faraday es igual a 9,6487; con π² – (1/ϕ – 1/ϕ²) se obtiene 9,6335, que es inferior de un poco más de 15 milésimos. (El lector se habrá dado cuenta de que, incluso en estos últimos casos, se podrían aplicar correcciones de una manera similar a la que hemos hecho arriba, y que no lo hacemos sólo por brevedad).

SEXTA PARTE: CIENCIA, NUMEROLOGÍA Y ASTRONOMÍA EN LOS ANTIGUOS CALENDARIOS

1) Después lo que hemos visto hasta ahora, no podemos descartar que todas estas aproximaciones a π y ϕ que encontramos en los antiguos monumentos y estos mismos monumentos no sean más que una manera que podríamos definir “hermética” de representar las leyes científicas. Leyes que nosotros concebimos y expresamos de manera totalmente o, como es natural decir, abismalmente diferente, hasta el punto de que es probable que para el occidental medio esta manera de concebir los números y las teorías matemático-científicas aparezca tanto obvia y sensata cuanto la manera pagana de creer que todo ser intramundano puede ser una divinidad. Una puerta o una fuente, aunque desde el punto di vista material aparezcan justo lo que son (puerta o fuente), desde el punto di vista espiritual son dos cosas muy diferentes para aquellos que las consideran literalmente como dioses o para aquellos que en cambio las ven como banales objetos cotidianos. Del mismo modo, los números que definimos “irracionales” son cosas muy diferentes para aquellos que los consideran sacramentalmente como atributos de la mente divina ( o incluso como nombres secretos de Dios que donan a sus sacerdotes la posibilidad de compartir el poder divino) o para aquellos que en cambio los conciben simplemente como interesantes y inagotables rompecabezas matemáticos (tal vez considerando las mismas matemáticas, fuera de sus aplicaciones científicas, como un interesante y inagotable rompecabezas). Para dar al lector una idea más clara de lo que podría estar escondido detrás de la aparentemente inexplicable pasión del hombre antiguo por la armonía entre los calendarios y la numerología hacemos la siguientes consideraciones. Si tomamos de nuevo los valores del ángulo mínimo y máximo entre los solsticios que son alcanzados durante un ciclo de precesión, es decir los 43 y 47 grados que en parte ya hemos analizados anteriormente, vemos que tienen entre ellos una relación que a primera vista puede aparecer anónima, ya que es igual a 47 : 43 = 1,093023. Pero si de esta cifra se quita 1, se obtiene 0,093023, que difiere sólo de un milésimo de la diferencia entre 2ϕ – π = 0,094475976. Aún más impresionante es el análisis de la relación entre el número de días de un año solar (365,25) y el de un año de las fases lunares (354,36), que tiene lazos matemáticos que parecen aún más estrechos con π y ϕ. De hecho, si dividimos 365,25 por 354,36, obtenemos una cifra igual a 1,03073…, que una vez más a primera vista puede parecer bastante insignificante. Sin embargo, su posible significado aparecerá de inmediato más claro si nos damos cuenta de que este número se desprende también de la fórmula 2ϕ : π = 3,236… : 3,141… = 1,030072…, y por supuesto también de ϕ : π/2, con una diferencia de menos de 7 diezmilésimos. Tal vez en este momento nadie se asombrará al descubrir que incluso la relación entre el ángulo máximo y mínimo de la tierra con respecto a la eclíptica y el entre el año solar y el de las fases lunares están entre ellos en una relación que, de nuevo, tiene lazos bastante estrechos con la relación áurea. De hecho, 1,093023 : 1,03073 = 1,060435807631484. Si de esta cifra se resta 1 y luego se multiplica el resultado por 10, tenemos 0,604, que difiere de 1/ϕ = 0,618033 de poco más de un centésimo. Si hacemos la relación con el resultado de 2ϕ : π = 1,030072, vemos que 1,093023 : 1,030072 = 1,061113203737214. Repitiendo la operación hecha anteriormente con este número (es decir, restando 1 y multiplicando el resultado por 10) vemos que la diferencia con 1/ϕ es inferior de 7 milésimos, ya que 0,618033 – 0,611132 = 0,006901. Si tenemos en cuenta la inclinación espiritual de estas personas, podemos asumir con seguridad que estas relaciones, sin embargo aproximadas, representen para ellas la confirmación indiscutible que π y ϕ son los números que están en la base de todos los ciclos cósmicos, ya que el orden establecido por ellos parece reinar, aunque de manera complicada, también en estas relaciones que aparecen completamente accidentales, y por lo tanto carentes de todo significado matemático y religioso (por supuesto, teniendo en cuenta el concepto de religión que se tenía en la antigüedad, y no el nuestro).

2) Para tener una idea del relieve que puede tener un descubrimiento de este tipo para personas que atribuyen una enorme importancia religiosa a las relaciones matemáticas entre los ciclos cósmicos, debemos tener en cuenta que un número similar al que resulta de la relación entre los 365,25 días del año solar y los 354,36 de las fases lunares resulta de manera aproximada también hacinedo cinco veces la raíz de ϕ, que es igual a 1,03053…, con una diferencia de un poco más de 2 diezmilésimos. Esto a su vez significa que podemos obtener una muy buena aproximación de π y ϕ transformando la ecuación que hemos visto en 2ϕ : √(√(√(√ϕ) = 3,14018. O, al revés, podemos obtener una muy buena aproximación de 2ϕ de la ecuación π x √(√(√(√π/2). De esto modo la relación entre la duración del año solar y la de las fases lunares parece revelar también unas relaciones secretas entre los dos números, de manera que, teniendo cierto tipo de creencias religiosas, esto bien podría representar una revelación de relaciones igualmente secretas entre las divinidades representadas por el sol y la luna. Hay que tener presente que esta impresión puede haber sido reforzada por el hecho de que también la relación entre la duración real del año solar y sus días considerados “puros” por los antiguos Egipcios y los Maya (360) tiene conexiones con π y ϕ, ya que 365,25 : 360 = 1,0145833. Este número es casi igual a 1 + [(1/ϕ)³ : 10] = 1,0145898; o, de un modo más directo, lo podemos obtener también de √(√(√(√(√(π/2) = 1,0142119, con una diferencia de 2 diezmilésimos. Además, la impresión de una relación esotérica entre estos números puede haber sido reforzada por el hecho de que incluso poniendo los días “puros” del calendario solar en relación con los días del calendario de las fases lunares, obtenemos de nuevo un número significativo en relación con ϕ, ya que 360 : 354,36 = 1,015916 es un resultado que se puede obtener con una muy buena aproximación también de √(√(√(√(√ϕ) = 1,01515…, con una diferencia de aproximadamente 8 diezmilésimos. De modo que el 360 se pone como una especie de número capaz de relacionarse de forma similar tanto con la duración del año solar como con la de las fases lunares, casi como una especie de divinidad intermedia, capaz de resumir en sí los poderes mágico-numerológicos de las otras dos. El todo puede aludir a algún tipo de consubstancialidad de las muchas divinidades celestes, que, aunque muchas, al final pueden parecer todas derivadas de una unidad primigenia (y esto era precisamente una creencia del Antiguo Egipto). De hecho, el mito citado por Frazer en “The Golden Bough”, donde Isis con una estratagema consigue apoderarse del nombre secreto del dios Sol-Ra podría estar aludiendo al hecho de que Sirio, la estrella que era un avatar astronómico muy importante de esta divinidad (otro, como conocido, era la Luna), en el Antiguo Egipto tenía un ciclo que duraba de manera casi idéntica a el del Sol (365,25 días). Así que “el nombre secreto de Ra” podrían ser justamente estos números sagrados – π y ϕ – y esas relaciones de que se puede deducir la duración del ciclo solar. Si ese es el caso, es evidente que, junto con los números, Isis lograría apoderarse del “poder de Ra” sobre los ciclos cósmicos, su duración y por lo tanto su secreta armonía. Pero, más allá de eso, podemos pensar que con π y ϕ podría estar en relación también esa “magia práctica” que en la época probablemente estaba considerada la ciencia empírica. De hecho, en los números asociados con los ciclos cósmicos había también los fundamentos de las leyes matemáticas que permitían al hombre de tener poder sobre la naturaleza. Esta forma de ver la ciencia, aunque diferente de la nuestra, al final no debería ser una sorpresa excesiva, ya que una fenomenología de este tipo también ha ocurrido en el caso del desarrollo de la ciencia moderna, aunque en una dirección que parece lo contrario. De hecho, la ciencia occidental actual, extremadamente laica, se deriva de investigaciones que en origen eran de tipo exclusivamente o casi exclusivamente astronómico. No hay que olvidar que la primera gran expresión de nuestra dinámica ha sido justamente la ley de gravitación universal, de la que luego han derivado todas las demás (por lo menos desde el punto de vista metodológico). Al final, el poder que tenemos sobre la naturaleza nos viene del interés de tipo religioso o casi-religioso que personas como Galileo y Kepler tuvieron por las “esferas celestes”, todavía consideradas en su tiempo como sede de lo divino y capaces de influir en el destino del hombre. A menudo nos olvidamos que Galileo escribió tanto de astrología como de astronomía y no está en absoluto claro – fuera de nuestros muy sólidos prejuicios culturales – si la astrología era considerada por él sólo una manera para hacer dinero. Hoy en día hay unos muy prestigiosos intelectuales ateos que sostienen que las matemáticas son contrarias al espíritu religioso y se olvidan de que incluso en el ámbito de nuestra cultura muchos de los más grandes matemáticos – Pascal, Descartes y Newton, sólo para nombrar unos que todo el mundo conoce – fueron al mismo tiempo también personas profundamente religiosas.

3) Si tenemos en cuenta eso, nadie se sorprenderá al descubrir que el antiguo calendario egipcio se creó de tal manera que las proporciones relativas al número de oro se pueden encontrar en diversas formas en las relaciones entre sus partes constitutivas. Por ejemplo, sabemos que los 360 días “puros” del calendario solar estaban divididos en 12 meses de 30 días cada uno, a los que se habían añadido 5 días “malditos” (recordemos que el número de oro está íntimamente ligado al 5, ya que se puede derivar de la fórmula ϕ = (√5 + 1) : 2; después lo que hemos visto más arriba, está claro que de la raíz de 5 podemos sacar también una excelente aproximación a π). Si dividimos el número de los días del mes por el número de los meses y añadimos al resultado la cifra que tenemos de los 5 días malditos divididos por el número de los días de un mes, encontramos que (30 : 12) + (5 : 30) = 2,5 + 0,1666… = 2,61666…, o un número que difiere de ϕ² de menos de un milésimo y medio, ya que ϕ² es igual a 2,618033. O bien, si observamos la sección áurea de los 360 días “puros”, vemos que ella se sitúa en el 222,49.no día del año, es decir en la mitad del decimotercero día del octavo mes. Si dividimos 13 por 8 tenemos un número que a su vez está muy cerca del número de oro, una cosa que resulta inmediatamente también de la constatación que el 13 y el 8 son, respectivamente, el sexto y el séptimo número de la serie de Fibonacci. De hecho 13 : 8 = 1,625, es decir una cifra que difiere del número de oro sólo de 7 milésimos. Si del Antiguo Egipto nos desplazamos a América del Sur y echamos un vistazo al sistema maya de Haab’-Tzolkin, podemos constatar que el primer calendario – el Haab’, que corresponde a un año solar – se componía de 18 meses de 20 días cada uno (con un total de 360 días, que agregados a los 5 días “malditos”, dan los 365 días del año solar), mientras que el segundo, el Tzolkin, se componía de 20 meses de 13 días cada uno. Si dividimos el número de los días del mes por el número de los meses del calendario Haab’ y, al revés, en el caso del Tzolkin, el número de los meses por el número de los días de un mes y después sumamos, vemos que (20 : 18) + (20 : 13) = 1,111… + 1,5384… = 2,6495, es decir un número una vez más lo suficientemente cerca de ϕ² (su raíz es 1,6277, con una diferencia de un poco menos de un centésimo con respecto del número de oro). Además, en el caso del calendario maya, dividiendo el número típico del calendario Haab’ por el número típico del calendario Tzolkin (es decir 18 y 13), vemos que 18 : 13 = 1,3846…, una cifra más o menos igual al resultado de la ecuación 1 + (1 – 1/ϕ) = 1 + 0,381966 = 1,381966. El revés de esta relación produce 0,7222…, es decir un número igual a un centésimo de la duración expresada en años solares de aquella unidad de tiempo fundamental para los antiguos pueblos que más arriba hemos definido como un Día de Precesión y que, aunque de manera compleja, hemos encontrado que está en relación con algunas constantes científicas. Sabiendo eso, hemos de inferir que también en la relación entre el 18 y el 13 deberíamos ser capaces de identificar estas relaciones. Y, de hecho, sólo como ejemplo bastante obvio, el resultado de 18/13, si multiplicado por 100 nos da el número típico del Día de Precesión y, al revés, dividido por 100, da 0,0072222…, es decir un número muy similar a 1/137,036, que es el número que expresa la fuerza electromagnética activa entre dos electrones, con una diferencia de 0,7 diezmilésimos.

4) El 18 y el 13 tienen también otras implicaciones interesantes de tipo numerológico-astronómico. Por ejemplo, si sumamos los resultados de 18/13 y 13/18 vemos que 1,3846 + 0,7222 2,1068, un número que difiere de poco más de 5 milésimos del resultado de la relación entre el ciclo de retrogradación de los nodos de la Luna (18,61 años solares) y el en que la Luna termina una vuelta completa con respecto a la posición de las estrellas en la esfera celeste (8,8564 años solares), ya que 18,61 : 8,8564 = 2,1013. Pero los resultados más importantes se tienen si comparamos estos números a los 47 y 43 grados que, como ya hemos visto, son respectivamente el ángulo mínimo y máximo entre los solsticios durante un ciclo de precesión. Comenzamos con el análisis de las relaciones numerológicas del 18 (más tarde veremos también el 13) con estos ángulos y en particular con un análisis del detalle del paisaje sagrado suramericano quizás más famoso, Teotihuacan, que podemos ver en el siguiente mapa

Como podemos ver, la Pirámide del Sol y la de la Luna están inclinadas entre sí por 18° con respecto al eje de la estructura, representada por la Avenida de los Muertos. Si dividimos los 47° del ángulo entre los dos solsticios por estos 18° vemos que 47 : 18 = 2,6111, es decir un número muy cerca del cuadrado del número de oro (2,618033, con menos de 7 milésimos de diferencia). Así que estos 18° serían una sección áurea, digamos, un poco extraña del ángulo entre los dos solsticios. Pero, como de inmediato se nota, 18° representan también un vigésimo del ángulo completo. De hecho, podemos pensar el ángulo completo como compuesto de 20 partes de 18° cada una; y esta subdivisión sugiere una relación con la subdivisión de los 360 días “puros” del año Haab’, que, como hemos visto, son divididos en 18 meses de 20 días cada uno. Observando estas dos subdivisiones que podemos definir iguales y opuestas del mismo número, el 360, parece que podemos entender que de esta manera se pretendía crear una especie de armonía al revés entre la vigésima parte del ángulo completo y la decimoctava parte de los días puros del año solar. Esto podría significar que los 18° de inclinación entre las dos Pirámides de Teotihuacan se refieren a la vigésima parte de la vuelta realizada por el Sol a lo largo del zodiaco durante el ciclo de precesión, que, como hemos visto, tiene una dirección opuesta al ciclo anual. Pues estos 18° podrían representar también la duración de un mes de precesión que debería ser igual a 26.000 : 20 = 1300 años solares, que a su vez son iguales a 250 Grandes Años (en el sistema maya de hecho era muy importante – como veremos en un trabajo siguiente – un período de 52 años solares Haab’, que fue llamado justamente Gran Año). Por supuesto, todo lo que hemos dicho acerca de los 18° de inclinación entre la Pirámide del Sol y la de la Luna en Teotihuacan, hablando numerológicamente, también se aplica al número 18 en cuanto número típico del calendario Haab’. Y también el 13, el número típico del calendario Tzolkin, mantiene con el 47 relaciones asociadas con el número de oro. De hecho, 47 : 13 = 3,61538, una cifra que está muy cerca del resultado de la ecuación 1 + ϕ² (la diferencia es de menos de 3 milésimos).

5) Pero, como ya hemos visto, si 47° es el valor del ángulo máximo entre los solsticios durante un ciclo de precesión, el mínimo es de aproximadamente 43°. Y también en este caso vemos que los dos números típicos del calendario maya tienen con este número una relación de tipo áureo. De hecho, tenemos que 43 : 18 = 2,3888, es decir un valor que es muy similar al resultado de la ecuación ϕ² – (1/ϕ)³, que es 2,381966, con una diferencia de sólo 7 milésimos. En cambio, si dividimos los 43 grados por 13, tenemos 43 : 13 = 3,30769, es decir un número que es muy similar al resultado de ϕ + ϕ = 3,236067976, con una diferencia en este caso de aproximadamente 7 centésimos. El número de oro y el Pi griego parecen además ser capaces de arrojar luz también sobre el enigma de la orientación “incorrecta” de Teotihuacan, un lugar diseñado de acuerdo con ejes muy inusuales, que tal vez el lector habrá vislumbrado en la imagen de arriba “El proyectista decidió que la ciudad tenía que estar construida de acuerdo con una parrilla orientada hacia “puntos cardinales”. Salvo que los “puntos cardinales” eran los que él mismo decidió: en cambio del norte utilizó la dirección 15.5 grados nordeste y en vez del este utilizó la dirección 16.5 grados sudeste (…). Es como si por alguna razón existieran un “eje norte-sur teotihuacano”, desplazado de 15.5 grados hacia el este con respecto del nuestro, en que estuvo orientada la Avenida de los Muertos, y un “eje este-oeste teotihuacano”, desplazado de 16.5 grados hacia el sur con respecto del nuestro (…). La precisión con que se llevaron a cabo las orientaciones muestra que el hecho de que el ángulo entre el eje T-norte-T-sur y el eje T-este-T-oeste no es recto (es decir de 90 grados), sino en vez de 91 grados, ciertamente es intencional y no se debió a un error”. Giulio Magli, Misteri e Scoperte dell’Archeoastronomia, Newton Compton, p.172. Para analizar este problema podemos partir de la constatación que si dividimos un año solar por el resto de 5,25 días que hallamos entre los 360 días “puros” del calendario Haab’ y su duración real de 365,25 días, llegamos a descubrir una relación bastante interesante. De hecho, se puede considerar un año solar de 365,25 días en lugar de como un período de tiempo como un ángulo de 365°,25; y si lo dividimos por los 5,25 grados-días que lo diferencian de un ángulo de 360°, aquí obtenemos un resultado igual a 360°,25 : 5°,25 = 69°,5714, o un ángulo muy similar al ángulo característico del Círculo Megalítico de Nabta Playa, que, como hemos visto en The Snefru Code, part. 5, es prácticamente igual a la sección áurea de la unidad del ángulo completo, es decir 180°. Pero si ahora dividimos por estos mismos 5°,25 los 16°,5 de deviación hacia el sur del eje este-oeste teotihuacano, quizás con un cierto grado de incredulidad descubrimos que hemos obtenido una aproximación a π que parece absolutamente idéntica a la que en la Gran Pirámide se expresa por la relación entre la mitad del perímetro y la altura. De hecho 16,5 : 5,25 = 22/7 = 3,142857. Y este hecho parece confirmar la hipótesis formulada en un reciente artículo en “World Mysteries”, en el que se observa que la disposición de las dos Pirámides de Teotihuacan tienen tales connotaciones por las cuales se pueden sobreponer a las de Keops y Micerino, como podemos ver en las fotos de abajo.

El argumento, como se comprende de inmediato, es realmente de muy gran interés, pero por razones de espacio aplazamos a The Snefru Code, part. 8 el análisis de las posibles relaciones entre la civilización del Antiguo Egipto y las precolombinas. Continuando entonces en nuestro análisis actual, si dividimos el ángulo mínimo alcanzado entre los solsticios durante el ciclo de precesión (43°) por los 16,5° de la orientación este-oeste “incorrecta” de Teotihuacan, llegamos una vez más a una buena aproximación de ϕ², ya que 43 : 16,5 = 2,606, con una diferencia de aproximadamente 12 milésimos de la cifra exacta. En cuanto a los 15,5 grados de desviación hacia el este del eje norte-sur teotihuacano, si dividimos el valor mínimo formado por el eje polar de la tierra con respecto del polo de la eclíptica por este valor, vemos que 21,5 : 15,5 = 1,387096, es decir un valor que más o menos es igual a ϕ – (1/ϕ)³ = 1,381966, con una diferencia de aproximadamente 5 milésimos. El significado de esta relación parece confirmado del hecho que si dividimos los 365,25 días de un año solar por estos mismos 15°,5, obtenemos un valor 23°,56, que es casi idéntico en esta ocasión a la desviación máxima del polo terrestre con respecto a la de la eclíptica. De los dados de la orientación “incorrecta” de Teotihuacan se puede deducir que entre el eje norte-sur y el este-oeste hay 91° en vez de los habituales 90°. Podemos interpretar este número extraño, a primera vista muy enigmático, poniéndolo en relación con los 91 escalones que en Chichen Iza forman la escalinata a lo largo de los cuatro lados de la Pirámide, que han sido interpretados como un cuarto de un año solar de 364 días. Sin embargo, mientras que en Chichen Iza el 365.mo es representado por la terraza que se encuentra en la parte superior de la Pirámide, en Teotihuacan no está claro cómo podemos completar la imagen del año solar (tal vez se puede llegar integrando en la interpretación también las llamadas “pecked crosses”, que de hecho parecen calendarios lunares; pero hay que reconocer que se trata de una operación muy complicada).

6) Sin embargo, observando que las relaciones entre los diversos ciclos celestes y los relativos calendarios (y teniendo en cuenta que también los paisajes sagrados como Guiza y Teotihuacan sin duda se pueden considerar como unos gigantescos calendarios de piedra) encuentran una especie de común denominador en π y ϕ, es natural suponer que en el pasado estos números han sido relacionados con las divinidades principales, en particular con el Sol y la Luna, y concebidos como sus “nombres secretos”. Y en este punto de nuestra investigación podemos entender por qué en la antigüedad era creencia generalizada que el conocimiento de los “nombres secretos” de las cosas daba poder sobre ellas, incluso si se tratara de divinidades muy poderosas. El poder aludido non era el que nosotros definimos mágico, sino un poder totalmente similar a aquél que el conocimiento científico da a los científicos. Si el “nombre secreto” de Ra estaba formado por aquellas entidades matemáticas – es decir π y ϕ – que constituían también la esencia de todas las leyes que ahora llamaríamos “científicas”, en la época estos nombres no sólo eran capaces de revelar la armonía secreta de los ciclos cósmicos, sino también de dar a sus conocedores el poder de compartir y dominar las fuerzas divinas que los movían. Al final, lo que distinguía el saber científico de estas personas del nuestro no es su contenido, sino la actitud espiritual que tenían hacia su forma matemática, que se sintió como una revelación de la esencia de la mente divina, y por lo tanto como algo profundamente sagrado. Y, más bien, por lo que se puede entender, en el ámbito de muchas antiguas culturas los números eran percibidos como los símbolos religiosos más poderosos y temidos, celosamente guardados y objeto de una transmisión exclusivamente oral-esotérica. Lo que puede explicar de manera convincente porque este saber matemático y científico no dejó otras huellas que estos monumentos de piedra que aún permanecen intactos casi desafiando el paso de los milenios (hay investigaciones científicas muy serias que afirman que dentro de cinco o diez mil años los únicos monumentos de que todavía se podrán encontrar rastros en la tierra serán una vez más las Pirámides de Guiza y Dahshur o las murallas de Cuzco o de Ollantaytambo). Una vez que entendemos esto, podemos entender también cómo pudo haber ocurrido una simbiosis entre la astronomía y la geometría entendidas como fundamentos de la teología y de todas las ciencias empíricas; una simbiosis que aparece realmente extraordinaria, fascinante incluso para el hombre moderno y que sin duda justifica en el hombre antiguo aquella pasión para la armonía entre los calendarios y la numerología que para nosotros hasta ahora era tan difícil entender. En efecto, ya que partiendo de los números de los ciclos cósmicos fundamentales siempre de alguna manera se llega a π y ϕ, es natural la hipótesis que los antiguos científicos pensaban que tales números deberían ser de alguna manera “ocultos”, en cuanto matrices también en las constantes de leyes científicas que a primera vista no tienen ninguna relación con la astronomía. Y hemos visto que esta creencia es matemáticamente demostrable, aunque con algún pequeño obstáculo que se puede fácilmente soslayar con aquellas correcciones que podríamos llamar “experimentales”, a las que estas personas podían una vez más atribuir un significado religioso. Con respecto a la ley de Newton, la fuerza de la atracción gravitacional – reescrita por medio de π y ϕ – podría aparecer, por ejemplo, de esta manera

F = G (m1 x m2) : d² = [(Djedefre x ) + ] x [(m1 x m2)] : d²

O bien, si tomamos una de las fórmulas más comunes de la mecánica cuántica – la utilizada para el cálculo de la energía de una onda – E = nħω – y la clásica de Einstein, en la que la energía se calcula con E = mc², podemos hacerlas objeto de una transformación interesante, sobre todo si tenemos en cuenta que en la fórmula de la mecánica cuántica π ya está presente, aunque no de forma explícita, ya que ω = 2πν. Por lo tanto, la misma fórmula puede escribirse por extenso de esta manera: E = nħ2πν. Usando el valor de ħ, que hemos obtenido anteriormente por medio de una función de ϕ, esta fórmula se reescribiría de tal manera que esa especie de abismo gnoseológico que la separa de la de Einstein tendería a descolorar en la dependencia que en ambas descubriríamos de π y ϕ, entendidas como constantes universales. El cálculo de la energía en estas dos teorías, a pesar de la diversidad lógico-matemática, volvería a tener algo en común (por motivos de oportunidad, excluimos los multiplicadores basados en las potencias del 10).

E = nħω = nħ2πν = n {[1 + (1 – 1/)³] 2π} ν

E = mc² = m [ – (1 – 1/)²]²

7) Pero el proceso de generalización podría no parar aquí, ya que, como hemos visto, podríamos llegar a obtener tanto π como ϕ por medio de los números del ciclo solar y de aquello de las fases lunares. Teniendo en cuenta que estos ciclos y los calendarios relacionados con ellos eran símbolos del Sol y de la Luna entendidos como divinidades, tendríamos como conclusión que en las teorías científicas y matemáticas del Antiguo Egipto estaban integrados unos símbolos religiosos en sentido muy estricto. Esto nos explicaría abundantemente porque estas personas no veían alguna diferencia entre matemáticas, geometría, numerología, astrología, astronomía y ciencia empírica en general: porque todas estas actividades para ellos no eran nada más que diferentes ramas de la misma ciencia, la teología, que todas las involucraba y las reunía en el fundamento de π y ϕ, entendidos como constantes universales presentes en la mente de Dios y por lo tanto como Ley de todas las leyes. Siguiendo la línea lógica dictada por esta hipótesis podemos pensar que en este tipo de ciencia los valores constantes – derivados conjuntamente de π y ϕ – debían tener un papel, diríamos, “ideológico” absolutamente predominante con respecto al papel de las variables, porque en un contexto de este tipo se podía atribuir a ellos el poder mágico-divino de mover el mundo. Esta es una manera de pensar en la que la contradicción entre el determinismo y el indeterminismo – que caracteriza el estado actual de nuestra ciencia y de nuestra investigación científica – podía no ser aquel drama epistemológico del que estuvo la causa cuando a principios del siglo pasado se descubrió por científicos crecidos en el culto de la infalibilidad del determinismo de tipo newtoniano (y que, por lo menos en parte, continúa también hoy en día). Al contrario esta contradicción podía ser vista como una apariencia o como algo sin importancia y transcendida en la adoración de lo que había en común entre las diferentes leyes, es decir, de aquel poder divino del que en π y ϕ se veía la expresión sagrado-matemática. De hecho, si se ven π y ϕ como instrumentos por medio de los cuales Dios o los dioses mueven el cosmos, entonces el hecho de que por un lado hay una “magia divina” caracterizada por la continuidad y el determinismo, y por el otro una “magia divina” en la que, en cambio, reinan la discontinuidad y el indeterminismo, sin duda puede ser un detalle insignificante. En ambos casos, los que creen que es la voluntad divina la causa eficiente del eterno retorno de los ciclos celestes y de lo que sucede en el mundo como su signo y reflejo, también pueden creer (y desde su punto de vista con todo tipo de buena razón) que Dios actúa en casos diversos por medio del poder mágico de leyes que, aunque aparentemente diferentes, tienen una raíz común en los números fundamentales que están en su mente (o tal vez que son su misma mente). Bien mirado, esta hipótesis histórica podía tener algún efecto sobre nuestra comprensión actual de la ciencia. Se puede pensar de tomar una tabla con todas las constantes fundamentales, en la que, en lugar de aparecer como números, ellas aparezcan como funciones de π y ϕ. Estas funciones sin duda aparecerían en relaciones muy estrechas, incluso se podría pensar que todas deriven de una matriz común y que se puedan ajustar a la realidad empírica por medio de correcciones que, como hemos visto, en algunos casos, son realmente insignificantes. Una tabla de las constantes estructurada de esta manera ayudaría a hacer que la ciencia (espontáneamente se diría: como por magia) no nos aparezca como un amasijo de técnicas de cálculo aparecidas quién sabe cómo y aplicadas de acuerdo a la mayor o menor comodidad y exigencia de exactitud, sino como una estructura que conserva siempre una fundamental unidad en torno a dos solos números fundamentales. Con esto habríamos descubierto la razón por la que en las relaciones entre las partes de la Gran Pirámide encontramos continuamente π y ϕ: porque la Gran Pirámide es un monumento que fue construido justamente para expresar la idea de que todo lo que sucede en el universo deriva de las funciones de π y ϕ.

8) Esta es en una manera de ver que a primera vista puede ser juzgada absurda por el hombre moderno, ya que puede parecer un típico ejemplo de lo que con cierto desprecio llamamos “el pensamiento mágico”, que creemos que hemos abandonado completamente desde por lo menos un par de siglos. Pero, hay que pensar con cuidado: en la actualidad y justamente como un hecho científico creemos que una masa pueda actuar a través del vacío sobre otra masa a una distancia potencialmente infinita. Fue precisamente esta consecuencia de su teoría que llevó a Newton a escribir las famosas palabras: “no compongo [una] hipótesis”, lo que significaba simplemente que una cosa de este tipo no se puede explicar con hipótesis científicas, sino sólo con la magia (recordemos que en el tiempo de Newton algo así como “una acción a distancia” era considerada inadmisible, ya que entonces se creía comúnmente que una causa física sólo se puede concebir como el impacto de un trozo de materia contra otro trozo de materia. Descartes, por ejemplo, explicaba el magnetismo con “átomos-tornillo” que, girando alrededor de la tierra, cuando se encuentran con cuerpos que contienen “átomos-tuerca” causan este fenómeno de atracción que actualmente en cambio se explica con la imagen del campo magnético, es decir con la idea de una acción a distancia). O, cuanto al mundo microscópico, hoy creemos que los electrones y el núcleo están en relación de equilibrio dinámico los unos con el otro porque intercambian constantemente fotones: un concepto que, a nivel macroscópico, es algo tan obvio como pensar que un edificio está unido porque los condóminos están constantemente intercambiando el apartamento. En general, cualquier persona que conoce, aunque de manera no profunda, los experimentos de la mecánica cuántica, estará al corriente de los numerosos fenómenos que no tienen ninguna relación con el sentido común y en cambio tienen muchas relaciones con el “pensamiento mágico” tan despreciado. Para darse cuenta sólo es suficiente echar un vistazo en los experimentos sobre la interferencia de doble rendija (en el tema Bohr dijo una vez que “si alguien comprende por primera vez la mecánica cuántica y no se queda completamente trastornado, esto significa que no ha comprendido nada”). Como se ha señalado en repetidas ocasiones, por muchos científicos – incluso Heisenberg – de las llamadas “fuerzas” o “campos de fuerza”, que imaginamos como las causas de los fenómenos mensurables, no sabemos nada más de los efectos, que precisamente son los fenómenos mensurables. Pues, esas “fuerzas”, a las que los atribuimos, no resultan en absoluto de manera directa y objetiva de los dados experimentales, aunque creemos muy firmemente que existen, sino de hipótesis adicionales que unen entre ellos estos efectos de acuerdo con una regla matemática y unas imágenes como precisamente los “campos de fuerza” constituidos de “ondas”. Pero hoy en día en el mundo científico hay mucha conciencia de que estas imágenes son totalmente prescindibles y que, por ejemplo, se podrían reconstruir todos los fenómenos del electromagnetismo pasando por alto las imágenes de las ondas y los relativos campos de fuerza incluso a nivel matemático (a pesar de que en este caso hay que usar ecuaciones más complicadas y por lo tanto aún más inconvenientes; por otro lado, ¿ no se dice a menudo que “la verdad es inconveniente”? ¿ cómo entonces inferir la falsedad de una teoría de su pura y mera inconveniencia? Al final, se podría llegar a sostener lo contrario, es decir que la inconveniencia de una teoría testimonia de su mayor proximidad a la verdad). Conscientes de esto, será difícil sostener que los que atribuyen la ocurrencia de los fenómenos a unos “números-fuerza” en lugar que a unas “fuerzas” sean en realidad sustancialmente diferentes de nosotros. En efecto, dado nuestro contexto cultural, a todos parece razonable atribuir el papel de causa eficiente a unas “fuerzas”. Pero en un contexto cultural completamente diferente sería igualmente razonable atribuir a la forma mágica del 360 el movimiento anual y de precesión de Sol a lo largo del zodíaco. A un hombre formado a descuidar sus propios prejudicios una manera de pensar como esta no aparece en absoluto más estúpida y supersticiosa que la de los que creen, por ejemplo, que las estrellas externas de las galaxias espirales no son arrojadas al vacío debido a una substancia – la “materia obscura” – que no se puede medir de alguna manera, pero que representaría la mayor parte de la materia que constituye el universo Supongamos que estamos en un contexto cultural donde aprendimos una versión de la ley de Newton en la que la constante G aparece como una función de π y ϕ. En este punto, ¿ sería locura creer que la acción de m¹ y m² ocurre por medio de una acción mágica de estas dos constantes (que, recordemos, en este contexto estarían presentes en todas las demás leyes científicas), en vez de por medio de una, no menos mágica, atracción a distancia que existiría entre m¹ y m² (y que de ningún modo se puede constatar de manera objetiva)?

9) Lo que, naturalmente, se opone a esta clase de razonamientos es que para nosotros “la cuenta sale”. Por esto queremos decir algo así como “a pesar de cualquier paradoja potemos actuar por medio de una técnica forjada sobre la base de muchas teorías matemáticas: ¡ no estamos ahí sólo para contar los días o los siglos que pasan!”. Por otra parte, también estas personas podrían decir lo mismo, ya que mediante el cálculo de los números obtenidos de otra manera se pueden obtener los mismos resultados que nosotros obtenemos. En cuanto a la técnica, un edificio como la Gran Pirámide nos muestra de manera no cuestionable que estas personas por sus ecuaciones habían conseguido una técnica muy eficiente (aunque en este momento no sabemos exactamente en qué consistía), que además tenía unos rasgos de extraordinaria eficacia, que nuestra técnica aún no ha conocido y sobre la cual apenas somos capaces de hacer algunas suposiciones. Si luego reflexionamos sobre nuestras creencias científicas – o sobre las que podríamos llamar nuestras “imágenes matemáticas guías” – cuanto al mundo microscópico de hecho debemos admitir que, conscientes o no, desde décadas hemos abandonado la idea de la naturaleza como mecanismo a favor de una idea que tiene relaciones muy profundas con el pensamiento mágico-numerológico. Para dar un ejemplo muy famoso, a través de las fórmulas de la mecánica cuántica creemos que una partícula no es un cuerpo que existe físicamente, sino una distribución de probabilidades que nos hacen capaces de observarla. Por lo tanto, creemos también que una partícula es algo que pasa de la existencia abstracta de un número a la existencia concreta de un cuerpo (aunque pequeño) en el momento en que la medimos. Y tal vez para un físico formado en la visión clásica newtoniana esto puede parecer una especie de blasfemia contra la racionalidad y el sentido común, ya que la operación de medida puede parecer un ritual mágico en el que de algo, que podríamos definir como un nada matematizado, es creado algo que existe realmente. Aparte de esto, de la imagen cuántica del mundo microscópico viene como consecuencia además que si encontramos un electrón en el punto “x” en vez que en el punto “y”, o si descubrimos que una cierta partícula de uranio decae y otra no (aunque por lo demás sean idénticas), esto no depende en sentido propio de unas “fuerzas” (o por lo menos: de unas fuerzas determinísticas, cuyos efectos son previsibles a priori y exactamente). Incluso, en el caso del colapso de la función de onda – donde se teorizan nada menos que unos efectos a distancias infinitas – ya no podemos hablar de fuerzas que se transmiten de un punto a otro del universo ni siquiera en sentido heurístico, ya que desde un principio Bohr explicó estos fenómenos con enlaces de tipo holístico-simbólico (es decir, en fin de cuentas, de tipo mágico) que la teoría establece entre partículas generadas en un estado de “entaglement” (“entrelazamiento cuántico”). Estas afirmaciones de Bohr suscitaron la oposición feroz de Einstein, que contra ellas luchó toda su vida, a pesar de que, irónicamente, fue justamente él que sugirió a Heisenberg que “Es la teoría que nos dice lo que podemos observar”: pero ¡ la teoría es, precisamente, un sistema de símbolos matemáticos! Por extraño que parezca, el punto de partida para llegar al principio de indeterminación – y, por tanto, al abandono de un mundo visto como un sistema de relaciones causa-efecto a favor de un mundo visto como un nexo mágico de símbolos matemáticos – fue el pensamiento del más famoso Premio Nobel del siglo pasado, no el de un chamán o sacerdote-astrónomo, aunque sus conclusiones no parecen finalmente tan diferentes como nos quieren hacer creer. Supongamos que un sacerdote-astrónomo cree que π y ϕ son capaces de mover tanto el cosmos macroscópico como el microscópico en cuanto expresiones matemáticas da la voluntad divina: ¿ podemos realmente decir que se mueve en un plano teórico tan distinto del nuestro? Bien mirado, incluso una onda de probabilidades es un sistema de números, no de fuerzas. Por lo tanto, no se ve dónde está la substancial y irremediable diversidad entre un sistema de creencias como el nuestro y otro en el que algunos números particulares (que, cabe señalar, entran en las ecuaciones como elementos fundamentales del cálculo) desempeñan aquel papel de “causas eficientes” que en nuestra ciencia se atribuye, por ejemplo, a los números relacionados a una onda de probabilidades.

10) El descubrimiento de que nuestras constantes pueden calcularse como funciones de π y ϕ también podría tener consecuencias sobre el estado de nuestras teorías, ya que en este punto podríamos llegar a suponer que estos valores que consideramos constantes en vez pueden variar según una determinada regla, aunque de momento esta regla no se conoce. Y esta hipótesis podría ser el punto de partida para llegar a resolver problemas que hasta ahora nuestra cosmología ha dejado sin resolver. Ya hemos mencionado arriba el problema de las estrellas externas de las galaxias espirales que según los cálculos que podemos hacer desde nuestras ecuaciones deberían ser arrojadas al vacío intergaláctico por la fuerza centrífuga, mientras en cambio, según lo que parece, siguen orbitando alrededor del centro de la Vía Láctea, probablemente desde unos millardos de años. Pero si suponemos que G no es un número constante que tiene validez en todo el universo, sino el resultado de una función que crece en proporción al valor de la distancia entre las masas en juego y al número de oro, podríamos de esta manera echar las bases de la comprensión matemática de aquella figura típica – la espiral de Fibonacci – que caracteriza todas las galaxias de este tipo.

¿ Qué significa este razonamiento? Significa que la figura que vemos diseñada en el espacio por galaxias espirales como las que podemos ver en las imágenes de arriba podría corresponder al diagrama de acrecimiento de la constante G con el aumento de la distancia de los cuerpos celestes del agujero negro que se supone que está en el centro de todas las galaxias de este tipo; y este diagrama de acrecimiento debería corresponder de alguna manera a la fórmula de la espiral logarítmica. El aumento proporcional de G de acuerdo con una función basada en ϕ y en la distancia haría de manera que el factor de la disminución del campo gravitacional representado por “d²” estaría parcialmente contrabalanceado. De esta manera podríamos explicar por qué las estrellas externas de las galaxias están sometidas a una fuerza gravitacional de intensidad mayor que la que se puede calcular en base a nuestras fórmulas actuales mediante la eliminación de un concepto tan problemático como el de la “materia obscura”, que parece crear más problemas de los que resuelve. Y que en los extremos de la galaxia el campo gravitacional debe ser más intenso de lo que creemos en base a nuestras fórmulas actuales, es evidente no sólo por el hecho de que las estrellas externas no son arrojadas al vacío intergaláctico, sino también por el hecho que las partes externas de la espiral galáctica parecen volver hacia el centro como si, en el momento en que fueron capturadas por el agujero negro, en un primo momento, por decirlo así, tienten de continuar su carrera hacia el exterior, pero luego, perdiendo masa y por tanto energía cinética a lo largo del camino, estén finalmente como “rebotadas” hacia el campo gravitacional del agujero negro, volviendo parcialmente atrás. Algunos podrían pensar que esta es una manera de resolver un problema físico con una arbitraria alteración de los cálculos por medio de instrumentos matemáticos que no tienen nada que ver con fenómenos observables. Por otro lado, la llamada “materia obscura” – por la cual en este momento se intenta explicar los fenómenos observables – es una entidad que, por definición, no es observable. Ni puede escapar a nadie el hecho que considerar el valor de G como una constante que vale en cualquier punto del universo no es que una mera suposición a priori. Si bien se mira, Newton ha incluido en su fórmula este valor no porque el valor corresponde de alguna manera a una entidad objetivamente medible, sino justamente porque es un instrumento para hacer salir la cuenta: pero sus cálculos se referían precisamente sólo al sistema solar. Si nos volvemos a objetos de dimensiones considerables como las galaxias para hacer salir la cuenta somos totalmente libres para suponer que lo que aparece como una constante cuando se refiere a sistemas gravitacionales de reducida dimensión, si lo proyectamos sobre sistemas mucho más grandes se convierte en una variable. El descubrimiento de la función que regula el acrecimiento de G basado en la distancia no rechaza la obra de Newton, sino que la lleva a cabo.

11) A estas reflexiones podemos y debemos añadir otra sobre el estado general de nuestra ciencia empírica. De hecho, conocemos cuatro fuerzas fundamentales que no tienen entre sí ninguna relación matemáticamente sensata y que, por el contrario muestran diferencias que las hacen parecer totalmente incompatibles. En particular, todos sabemos que la masa atrae inevitablemente otra masa y no hay el contrario de este fenómeno, que en vez es típico de las fuerzas electromagnéticas. Y es también por eso que no se puede encontrar un nexo entre las fuerzas de gravedad y los fenómenos de magnetismo si no en el factor de decrecimiento de la intensidad de la fuerza de atracción (o, en el caso del magnetismo, también de repulsión) representado por “d²”. Pero hoy en día, incluso por parte de la arqueología estamos empujados a suponer que nuestra teoría de la gravitación es incompleta, ya que es muy difícil imaginar que esos colosos que pesan cientos de toneladas que se pueden encontrar en Egipto y en América del Sur se han podido mover de otra manera que a través de una inversión del signo de su campo gravitacional. Hemos visto antes cómo se ha movido el millar de toneladas de la Piedra de la Luna sin todos aquellos equipos industriales que serían absolutamente indispensables para nosotros sólo para poder imaginar de hacerlo. Pues, una empresa de este tipo pudo realizarse sólo por quien de algún modo era capaz de hacer de manera que esta enorme masa se comporte respecto a la tierra un poco al igual de las cargas eléctricas cuando son del mismo signo y muestran la tendencia a rechazarse entre sí. Sólo de esta manera el desplazamiento de esta piedra podía prescindir de máquinas gigantescas, que a su vez presuponen un aparato industrial capaz de producirlas. Esto aparato, a su vez, presupone la explotación de los combustibles fósiles por medio de minas y pozos de petróleo, de plantas para la producción de electricidad, líneas de alta tensión para llevarla, una industria química y metalúrgica capaz de producir todas aquellas sustancias artificiales necesarias también a máquinas tan sólo mínimamente avanzadas y todos los demás elementos que han sido y siguen siendo indispensables para nuestro aparato técnico y de que, en cambio, en nuestro pasado prehistórico no hay la menor huella. Pero, bien mirado, incluso en casos menos extraordinarios que el de Baalbek por muchas razones nos vemos obligados a asumir una ciencia y una tecnología muy desarrolladas para poder comprender algunos restos arqueológicos que, de otra manera, son enigmáticos, si no de todo absurdos. Por ejemplo, el Templo del Sol que se encuentra en Ollantaytambo fue construido con piedras de tamaño muy grande, que se obtuvieron de una cantera que se encuentra en una montaña situada en el lado opuesto del valle. El camino que conduce de la cantera a Ollantaytambo es un sendero de cabras que baja hasta un río, que hay que vadear, y luego sube a la cima, donde se encuentra el templo: en total unos cinco o seis kilómetros de sendero escarpado y desigual. La razón por la cual podemos estar casi seguros que los constructores utilizaron estos caminos – que apenas podría recorrer un todoterreno – es que aún hoy hay piedras que han sido abandonadas por razones desconocidas en el camino. Estas piedras han sido bautizadas por los nativos con un nombre muy significativo “piedras cansadas”, aludiendo oscuramente de esta manera a un medio de transporte como para sugerir que las piedras se movían por su cuenta, sin la contribución de la fuerza física de seres humanos. También podemos estar bastante seguros de que el río se vadeó, porque no se han encontrado restos de cualquier puente y casi non se puede creer que no dejen huellas de un puente que puede soportar decenas de toneladas de carga. Es cierto que las “piedras cansadas” llegan al tamaño de las que forman el templo propiamente dicho, pero hay algunas que parecen llegar aproximadamente a las veinte toneladas. Y aún en casos como estos estamos obligados a asumir que los que las llevaron hicieron uso de algo así como una inversión del campo gravitacional, porque en la actualidad, incluso para desplazar cargas de este tipo, nuestra tecnología no podría de ninguna manera funcionar en caminos de cabras, sino como mínimo, en carreteras asfaltadas y realizadas de manera profesional. En cambio, para las piedras de tamaño doble o triple que en realidad han sido usadas para construir el templo (que pesan por lo menos cincuenta toneladas) hasta la fecha no hay ninguna máquina que puede – no digamos llevarlas por kilómetros cuesta arriba y abajo a lo largo de caminos de cabras en algunos lugares muy empinados, como se debería hacer en Ollantaytambo – sino sólo para levantarlas y moverlas unos pocos metros sin estructuras que requieren una transformación total del territorio. Consideremos que hoy en día las grúas más potentes que tenemos pueden mover un máximo de alrededor 200 toneladas de peso. Sin embargo se trata de aparatos muy complicados y de enorme tamaño (cuando se ven desde la distancia parecen altos como un edificio), que para cada operación de movimiento requieren semanas de preparación y grandes espacios especialmente preparados, no senderos.

12) Así, a partir de nuestras teorías físicas y nuestra técnica podemos desde luego definir un templo como el de Ollantaytambo (como por otra parte la plataforma de el de Baalbek o los colosos de Memnon o las murallas de Alatri) como objetos imposibles. Objetos imposibles que pero están ahí, ante nuestros ojos: bloques que pesan cientos de toneladas fueron efectivamente transportados y colocados donde todavía se encuentran hoy en día. Y este hecho nos empuja a asumir que nuestra teoría gravitacional es incompleta, que un campo gravitacional se puede invertir, de manera similar a la que hacemos con un campo magnético (o incluso que en una nueva teoría la fuerza de gravedad puede convertirse en una parte o una expresión de las fuerzas electromagnéticas). Esto en el momento nos puede aparecer algo absurdo o impensable. Pero no parece posible imaginar de otra manera la construcción de monumentos megalíticos como los que se pueden observar en todo el mundo sin una transformación simultánea de los alrededores por medio de estructuras industriales más o menos extendidas que sin embargo de hecho no resultan de ninguna manera verificables. De esta observación podría nacer una tentativa de desarrollar nuestra teoría gravitacional hasta el punto de entender la naturaleza de esta nueva fuerza, que sea algo así como un polo negativo del campo gravitacional, que hasta ahora ha escapado a la comprensión de nuestra ciencia empírica. Por supuesto, nos damos cuenta de que todas estas indicaciones pueden aparecer en este momento arriesgadas, pero el descubrimiento de un diagrama del espacio-tiempo cifrado en el espacio sagrado del Antiguo Egipto hace sensata una investigación en este sentido. Además, si se pudiera comprobar el conjunto de estas hipótesis, las consecuencias serían verdaderamente importantes. Sabríamos entonces que no sólo Guiza y Dahshur son las imágenes del cielo de la Duat en 10.500 a. C., sino también el paisaje sagrado – en el conjunto y en sus partes, en su cuerpo arquitectónico tridimensional como en el espacio decorativo bidimensional – fue diseñado y construido de una manera tal que represente un conjunto de teorías físicas, geométricas y matemáticas imaginadas como ciencia de lo divino (porque parece claro que, una vez aceptada la presencia del diagrama del espacio-tiempo en la Gran Pirámide, es difícil imaginar que los antiguos Egipcios no conocían también todas las demás teorías que son la presuposición y la consecuencia físico-matemática del mismo diagrama). Estas teorías, nacidas quién sabe cómo y quién sabe dónde, estaban destinadas a desaparecer en el olvido, de manera para nosotros no más clara de la con que fueron descubiertas, para ser redescubiertas en Occidente miles y miles de años más tarde, con formas y finalidades diferentes de aquellas que tenían entre nuestros lejanos antepasados. Con todo eso habríamos demostrado que – a pesar del poder enorme y cada vez mayor de la técnica que nuestra ciencia nos hace disponible – nuestra ignorancia de qué es el hombre y cuál es el significado de su presencia en el cosmos está aún bien lejos de ser anulada.

APÉNDICE 1: UN BOSQUEJO DE LA TEORÍA DEL CAMPO UNIFICADO PROBABLEMENTE CODIFICADA EN LA GRAN PIRÁMIDE

1. En 1836-1837 Howard Vyse, durante un período de excavaciones intrusivas realizadas en la Gran Pirámide por medio de la dinamita, descubrió en la salida del Pozo Sur de la Cámara del Rey (el que apunta hacia el Cinturón de Orión ) una plancha de forma rectangular. Su longitud era de aproximadamente 304,8 mm, su anchura de 101,6 mm, su espesor de 3 mm. Estas dimensiones no parecen nada de casual, ya que incluso a simple vista vemos una proporción cerca del 3 parece tener un papel especial en su determinación. Así podemos tratar – como un experimento mental – de reconstruir su tamaño a partir de los números que para los Antiguos Egipcios eran muy importantes, suponiendo se hayan tomadas las medidas con un mínimo de aproximación . Así, suponemos que el espesor se ha determinado con la fórmula 2ɸ (o √5 + 1) y que, por tanto, fuera originalmente 3,23606 … mm . Luego suponemos que el ancho se determinó por la fórmula 2ɸπ x 10, y que fuera originalmente 101,66407 … mm . En cuanto a la longitud , suponemos que se puede determinar usando la constante que se utiliza para calcular la velocidad de la luz , que es igual a 2.9979246. Así que la longitud sería el resultado de la fórmula 2ɸπ x 10 x 2.9979246 = 304.7822 . La diferencia con respecto a la medida de la longitud que se toma generalmente como justa sería de poco menos de dos décimos de milímetro . Si este experimento mental se correspondía con la realidad, tendríamos que la velocidad de la luz no habría sido codificada sólo en las medidas de la Gran Pirámide, sino incluso en esta placa de hierro aparentemente anónima, que había sido colocada en el extremo del pozo sur de la Cámara del Rey. Bouval y Hancock han comisionado algunas pruebas científicas, que han demostrado que el hierro no era de origen meteórico y que, muy probablemente, in origen era dorado. Este último hecho es muy importante en relación con nuestra hipótesis, porque el oro se puede considerar la mejor metáfora de la luz, de la cual la placa contendría una característica fundamental. Tampoco podemos descartar la posibilidad de que incluso los otros números que caracterizan el objeto contengan otra información científica y astronómica. El caso del sarcófago de la Cámara del Rey nos ha enseñado que por medio de medidas que en nuestra cultura se consideran triviales se pueden codificar datos científicos que eran muy importantes para esas personas, sobre todo porque se consideraban directamente relacionados con el cosmos concebido como el fruto de la obra de un divino arquitecto. Pero veremos estas cosas de manera profunda y detallada en el Código Snefru 7. Por ahora nos limitamos a un solo ejemplo, que pero consideramos muy importante. Si tomamos la longitud de la placa en decímetros vemos que es 3,047822 . Si hacemos la división entre π y este número llegamos a un resultado igual a π : 3.047822 = 1.030766 , una cifra que parece a primera vista bastante insignificante. ¿Qué podemos decir , cuando nos encontramos con el hecho que la proporción matemática entre el número de días de un año solar (365,25) y lo de un año de fases lunares (354.36) nos da un número casi igual a este, es decir 1,03073 … ? Un número muy similar se puede conseguir también desde 2ɸ : π = 3.236 … : 3.141 … = 1,030072 … y por supuesto también por ɸ : π/2 . Además, teniendo cada centímetro como el equivalente de un millón de kilómetros, vemos que la longitud de 304.78 mm corresponde casi perfectamente al doble de la distancia máxima entre el Sol y la Tierra , que es igual a 152.100.000 kilómetros (x 2 = 304,2). También podemos notar que, en términos de númerología, hay una gran similitud entre la distancia media de la Tierra y el Sol y la velocidad de la luz dividida por dos (149.59788 contra 149.89623). Una cosa para nosotros sin ninguna importancia, que pero para aquellas personas podría tener un significado simbólico muy importante.

2. Recordemos también que el Pozo Sur de la Cámara del Rey apunta al cinturón de Orión. Alnilam , la estrella central y más brillante, se encuentra a unos 1.000 años luz de la Tierra. Si tomamos cada décimo de milímetro como un año luz , se podría suponer que la anchura de la placa (1016 décimos de milímetro) representa la distancia entre la Tierra y Alnilam en años luz (es decir, en términos de tiempo), mientras que la longitud la representa en términos de espacio (puesto que la longitud es la anchura multiplicada por la constante de que se obtiene la velocidad de la luz). No es imposible que incluso el tamaño de la Cámara del Rey y la Reina contengan referencias similares a Orion y/o a otras estrellas y constelaciones que para los Antiguos Egipcios eran muy importantes. Por ejemplo , su longitud (que se mide en el eje Este-Oeste) es de unos 10 metros: tomando cada décimo de metro como un año luz, tenemos una vez más la distancia de la Tierra y Alnilam (tengamos en cuenta que en Giza, en el equinoccio vernal, Orión sale en dirección este). Otros datos interesantes se pueden derivar de los ángulos característicos de las Pirámides . Por ejemplo, el ángulo de la base de la Pirámide Acodada es de aproximadamente 54° 30′. Si con una operación numerológica transformamos los sesenta de un grado en centésimas de grado, tenemos un ángulo casi idéntico a 54°303…: si sumamos el seno y el coseno de este ángulo tenemos la raíz cúbica del número de Euler. Este número lo encontramos también codificado en las medidas de la Gran Pirámide, ya que el lado es de 440 codos y 440 : e = 161,8670629957179 . Al dividir este número por 100 hemos 1,61867062 . Y el número de oro es 1.618033 … , y el número de oro aproximado que se puede obtener de la Gran Pirámide es igual a 1.61859… El ángulo de la base de la pirámide de Micerino es 51°,367 . La tangente de este ángulo es igual a 1,2511 , un número muy similar a √π/2 = 1,25331… ( si la tangente es igual a √π/2 el ángulo es de 51°,4141). El ángulo de la base de la Pirámide Roja es de aproximadamente 43°35 . Multiplicado por 2 nos da un ángulo de prácticamente idéntico a 86°,7812… : en este caso la suma de seno y coseno nos da 1.054571 … , que es el valor de ħ, una variante de la constante Plank desarrollada por Dirac (una muy buena aproximación a este número es la suma de seno, coseno y tangente de un ángulo igual a π/2; el resultado de esta suma es 1,054458 …; utilizando el valor de π que encontramos en la Gran Pirámide (22/7) el resultado es 1,054480 …: de esta manera descubrimos que dos datos empíricos – que por lo general tendemos a juzgar al azar y no ulteriormente explicable – el mínimo error posible en la determinación de la posición y velocidad de una partícula y el cuanto de acción – están contenidos en un valor geométrico fundamental que hasta ahora se creía completamente abstracto y divorciado de la realidad empírica , ya que tenemos que seno π/2 + coseno π/2 + tangente π/2 ) x 2π = h, la constante de Plank. Esto significa, por ejemplo, que la fórmula para derivar el número cuántico principal (n) que escribimos n x h/2π después de haberla derivada a través de una investigación empírica muy laboriosa, hubiera podido ser derivada con un procedimiento a priori, llevado a cabo sobre bases exclusivamente trigonométricas . Esta extraña afirmación se vuelve más convincente como nos encontramos con que, por extraño que pueda parecer, podemos derivar un valor muy cercano a la constante de Plank dividiendo el ángulo redondo para aquel de 54°,3718624…, que tiene como característica fundamental que sustrayendo el seno y el coseno de la tangente tenemos 0 come resultado. Simbólicamente, esta parece una cosa muy importante : es como si estuviera inscrito en la trigonometría el hecho empírico de que , en virtud de una cierta cantidad , la transmisión de la energía es igual a 0 (señalamos de paso que el ángulo del vértice de la Gran Pirámide es extraordinariamente cercano al doble del ángulo de 38°,1727…, que tiene como característica fundamental que la diferencia entre el valor de la tangente y lo del coseno es igual a 0) :

360° : 54°,3718624… = 6,62107… (la constante de Plank se calcula actualmente igual a 6,62559…).

Si multiplicamos esto mismo ángulo por (1/ɸ x π² ) + 1/ɸ tenemos que 54, 3718624… x 6,7177… = 365,2584 … , es decir, la duración de un año solar. En cambio, si dividimos la longitud de un año solar para por aproximación de h, tenemos que 365,25 : 6,62107 … = 55,164799 … ; si hacemos la suma de seno, coseno y tangente de este ángulo llegamos a un resultado de 2,8289… , una cifra que es prácticamente idéntica a 2√2. Un número prácticamente idéntico a √2 es la tangente del ángulo que sale de la relación entre la longitud del año solar y la constante gravitacional , ya que 365,25 : 6.673… = 54°,736 … , ángulo cuya tangente es igual a 1.41425… (√2 = 1.41421…) .

3. Por lo tanto, es posible que la placa descubierta por el coronel Vyse, lejos de ser un objeto trivial, pueda contener importantes nociones científicas, que llegan a niveles inimaginables de sofisticación. De la cara más grande de la placa se pueden crear dos triángulos rectángulos cuya hipotenusa coincide con la diagonal del rectángulo. El ángulo opuesto del cateto menor es de 71°,5531526028 , cuya tangente es igual a 2,9979245999 … : esta cifra es casi exactamente la misma que la constante de la que podemos derivar la velocidad de la luz, que, como hemos visto, es igual a 2,9979246 . Pero el ángulo más interesante es sin duda lo de 66°, 2699 , desde el cual de nuevo podemos derivar un valor casi idéntico a “c”, haciendo tg x (sin + cosen ) = 2.9979222 … Aquí , lo importante da tener en cuenta es que este ángulo se puede obtener con buena aproximación por vía numerológica, haciendo el producto de h x 10 = 6,62599 x 10 = 66,2599 (la diferencia es de un décimo de grado). Este particular crea una conexión profunda con el sólido de que nos ocupamos. En efecto, empezando de nuevo el análisis de la placa que se fue hallada al termino del conducto de ventilación Sur de la Cámara del Rey, si multiplicamos el coseno de 71°,5531526028 (0,316424771589, un número más o menos igual a π/10) para la tangente obtenemos un número igual a 1,055479419, que corresponde casi a la perfección a “ħ” , el valor con el cual frecuentemente se reemplaza “h”, la constante de Plank ( ħ= h /2π = 1.054571). Un valor aún más aproximado se puede obtener dividiendo la hipotenusa por el cateto mayor, ya que 321,289 : 304,781 … = 1,05416554 , con una diferencia en comparación con el valor de nuestra constante de unos 3 diezmilésimos. Parece muy interesante de notar que un valor muy cerca de ħ puede ser obtenido con buena aproximación incluso desde 130√103 = 1,054573667…. Si operamos numerológicamente con esta ecuación dividiendo el exponente de la raíz por lo de la potencia tenemos que 130 : 3 = 43,333…, que es el ángulo de base de la Pirámide Roja expresado en grados y sesentavos de grados; el ángulo reciproco de este sobre el cuarto de giro tiene una tangente de 1,05378, un número una vez mas muy cerca de ħ (el ángulo que tiene la tangente exactamente igual a ħ es lo de 46°,52; la suma de seno y coseno de esto ángulo es casi idéntica a √2)). El coseno de el ángulo de 71°,5531526028 tiene una característica che parece muy interesante. Si lo multiplicamos por 10 y después hacemos la raíz quindécima tenemos que 15√coseno di 71°,55… x 10 = 15√3,1642477… = 1,07981999… ≈ 2ɸ/c = 3,23606… : 2,9979246 = 1,079436. En esto contesto parece también muy importante notar que si dividimos el perímetro de base de la Gran Pirámide por 6 veces la altura tenemos que (440 x 4) : (280 x 6) = 1760 : 1680 = 1,047619… ≈ π/c = 1,047922. Si en vez de multiplicar la altura por 6 la multiplicamos por la constante de Plank h, podemos llegar a ħ en esta manera: 1 : [(440 x 4) : (280 x 6,626)] = 1 : (1760 : 1855,28) = 1 : 0,9486… = 1,054136363 ≈ ħ = 1,054571. Tornando al plato objeto de la nuestra análisis, parece claro que – en vez que utilizar la relación entre el coseno y la tangente – podemos obtener la misma aproximación de ħ dividiendo la hipotenusa por el cateto mayor, ya que 321,289… : 304,781… = 1,05416554, (con una diferencia en relación al valor de la nuestra constante de circa 3 diez milésimos). Además, si dividimos el ángulo redondo por este ángulo multiplicado por π , tenemos que 360 : (71°,55315 … x π) = 1.601488…, un valor que es muy cerca de la medida en joule de un electrón-voltio (1,60217653) y prácticamente idéntico a la aproximación al número de oro que se encuentra en la pirámide de Micerino. El ángulo de 71°, 5531526028 es numerológicamente muy cerca de la duración en años solares del Día Precessional, resultante de la división de los 26.000 años de un Año Precessional en 365 partes en lugar de los canónicos 360, que es igual a 71°,2328 (un ángulo muy similar también se obtiene a partir de la relación entre el cuarto del circulo y la raíz cúbica de dos, es decir desde 90 ° : ³√2 = 71 °, 433). Multiplicado por π este mismo ángulo da un resultado de 223 °, 784, una cifra que es muy similar a la sección de oro del círculo (222.49). Sin embargo, el producto del valor exacto de ħ multiplicado por lo que se obtiene la velocidad de la luz da un resultado igual a 3,1615243433466 . Este valor corresponde a la tangente de un ángulo de 72 °,4476, que numerológicamente corresponde casi a la perfección al número de años que dura un día Precessional Canónico, que es igual a 26.000 : 360 = 72.2222 o incluso a 90 ° : ᴾᶦ√ 2 = 72 °,180.799 (curiosamente , la quinta raíz de 360 da un resultado de ⁵√360 = 3,24534, muy similar a 2ɸ , que corresponde al espesor de nuestra placa: en cambio la π-raíz de la duración exacta de un año solar es igual a ᴾᶦ√365,25 = 6,5418 , un número muy similar al valor de “h” si se calcula en erg por segundo (el número real es 6,55; recordamos que 10 elevado a 3.1646… nos da 1461, es decir la duración del ciclo de Sirio: la conexión numerológica con el volumen del Arca (una cosa che vamos a ver en un momento) parece por lo tanto razonablemente importante, y aún más significativa nos parecerá si tenemos en cuenta que ħ x 3.1646 x 2 = 6.67461 … , que es una muy buena aproximación de G, la constante gravitacional elaborada por Newton)). El ciclo solar anual y la precesión son tal vez un elemento de singularidad, casi las huellas digitales de la Tierra en relación con los otros cuerpos que mueven en el universo. Pero en los números típicos de estos ciclos, como parece , se encuentran codificadas las constantes de nuestras más importantes leyes científicas. Así, los antiguos calendarios contienen probablemente, aunque de modo hermético, los números fundamentales de todas las leyes fundamentales de la física. Vamos a discutir más profundamente sobre estos temas en The Snefru Code parte 4 y 7. Aquí, por brevedad, nos limitamos a un solo ejemplo. Pi griego – la constante que se utiliza para determinar el círculo y , como hemos visto anteriormente, incluso la constante de Plank – junto con ɸ está contenida en los ciclos cósmicos fundamentales que afectan a la Tierra. Esto significa que los hechos empíricos están contenidos en los números fundamentales de las leyes físicas que los describen. Por ejemplo, la tangente igual a π es característica de un ángulo de 72°34… , que en términos de númerología es prácticamente idéntico a una unidad de tiempo esencial para los antiguos, es decir el Día Precessional (que, recordemos, es igual a 72,2222 años solares). Pero en π, como hemos visto , están contenidos los dos números fundamentales de la mecánica cuántica . Así nos enteramos de lo que Platón quiso decir cuando dijo en el Timeo que

“Construyó la tierra para que sea nodriza nuestra y, por medio de su rotación alrededor del eje que se extiende a través del universo, guardia y artesana de la noche y del día, la primera y más anciana de las divinidades que hay en el universo. ”

Con estas palabras Platón no quiere decir que el universo gira realmente alrededor de la Tierra, pero que los números fundamentales que con contenidos en los ciclos cósmicos terrestres – que a su vez contienen esos de les leyes fundamentales de la física y de las geometría – son la forma lógica de todos los eventos que en el universo puede ocurrir.

4. De hecho, esta tesis platónica parece realmente tener algún fundamento. Más allá de lo que ya hemos dicho, podemos añadir que la relación que hemos visto anteriormente entre la constante de Newton (G) y la de Plank (h) parece en parte contener y en parte aludir a las relaciones armoniosas entre el mundo abstracto de las teorías geométricas y lo de los ciclos astronómicos de la Tierra. Por ejemplo (G/h)8 = 1,054897… es un número extraordinariamente cerca de ħ. Elevado al 72mo exponencial (recordemos que el 72 es un número-medida típico del ciclo de precesión) nos da (G/h)72 = 1,617677…, un número que difiere de menos de 3 diezmilésimos del número de oro. El número que sale de G/h parece tener un significado también por otras relaciones que se pueden construir con otras constantes físicas que tienen que ver con la estructura del átomo. Por ejemplo, el radio clásico del protón es igual a 1,535 × 10-18 m, mientras lo del electrón es 2,8179403267 x 10-15 m . La relación de estas longitudes (excluyendo las potencias de 10 ) es igual a 1,535 : 2,817940367 = 0,54472408 …. Este número – elevado al cubo – es igual a 0.161632 … , un valor muy similar al ɸ/10 . O bien, multiplicado por 2 y luego elevado a la sexta potencia nos da (0,54472408… x 2 )6 = 1,08944817 …6 = 1,67201227 … .. que es un valor muy similar a lo de la constante que se utiliza para calcular la masa en reposo del protón, que es igual a 1,6726231. Señalamos de paso que este valor puede ser reconstruido también por vía cosmológica. Osiris-Orion desaparecía desde el horizonte por circa 70 días y si dividimos los días “puros” del calendario Antiguo Egipcio por estos 70 obtenemos un valor igual a 5 + 1/7. Si después dividimos 70 por 5 + 1/7 obtenemos 13,6111… Si dividimos 5 + 1/7 por 13,6111… llegamos por fin a 0,377842… Este valor, multiplicado por π y elevado al cuadrado nos da 1,67256, es decir un valor muy cercano a lo de la constante que necesitamos para obtener la masa en reposo del protón. Lo que sea, prosiguiendo en nuestra análisis, si se divide G/h para ese número (1,67201227) tenemos que 1,0067028 : 1,67201227 = 0,60209 … un valor que corresponde a la carga eléctrica del protón menos 1, ya que, de hecho, 1,602 – 1 = 0,602 (1/0,602 = 1,6608 …, un número muy cercano a la constante que se puede usar para transformar los sesentavos de grado en centésimos de grado). Una relación sorprendentemente similar existe también entre la constante del momento magnético del protón 2.793 y la de su masa en reposo, dado que 1,6726231 : 2,793 = 0,598862 (la diferencia con la carga eléctrica esta vez es de aproximadamente 1 + 3,14 milésimas (cerca por lo tanto, a 1 + π/1000)). La masa de un electrón (me) es aproximadamente 1/1836 veces la del protón (mp) porque

mp/me = (1,6725 x 10-27) : (9,1091 x 10-31) = 0,1836076 x 104 = 1836,076

Si hacemos la relación entre el radio clásico del electrón (re) y el del protón (rp), vemos que esta relación parece invertirse exactamente, ya que, a pesar de su menor masa, el radio del electrón parece igual a lo del protón multiplicado por un número muy , muy similar a lo que pone en relación las dos cantidades de la masa

re/rp = 2,8179403267 x 10 – 15 : 1,535 x 10-18 = 1,835791.. x 103 = 1835,791…

1836,076 – 1835,791 = 0,28

Por lo tanto, como hipótesis heurística, se podría pensar que la masa es inversamente proporcional al espacio ocupado por la carga eléctrica, dado que el radio del protón es de aproximadamente 1/1836 el del electrón. De esto podemos deducir que la masa (y por lo tanto el campo gravitacional expresado por la masa) no es otra cosa – por así decirlo – que energía magnética concentrada . Así, hipotéticamente , si pudiéramos concentrar la energía del electrón en un radio equivalente a lo del protón , se podría aumentar su masa en proporción . A la inversa, la expansión del espacio ocupado por la carga eléctrica del protón reduciría su masa (y por tanto su peso ) a un valor similar a la del electrón. Y esta podría ser la forma en la que en la antigüedad eran capaces de mover estos bloques de granito monstruosos , que llegaban a pesar más de mil toneladas , que hoy en día no seríamos capaces de mover incluso utilizando nuestra tecnología más avanzada. Además, es posible que esta operación pueda crear un desequilibrio químico-magnético tal que el material más duro puede ser reducido a un estado pastoso. Esto explicaría la extraordinaria facilidad con que personas como los Antiguos Egipcios podrían trabajar piedras como la diorita con la misma eficiencia con la que nos trabajamos el plástico o el aluminio (y aquí tenemos también un indicio de lo que Platón pudo entender con un término como “condensación”). Si esta hipótesis corresponde a la realidad , sería posible construir dinamos que giran mediante lo que podríamos llamar una especie de “volante gravitacional” , que a su vez podría funcionar sin la ayuda de la electricidad producida por las centrales, que requieren el uso de minas de carbón, o de pozos de petróleo, redes de transmisión de alta tensión, etc. Y eso explicaría por qué los constructores de las pirámides podrían tener acceso a la energía sin la necesidad de todos los equipos que necesitamos en nuestro tiempo . Además, puesto que el campo gravitational se deriva de las cargas opuestas , su acción puede a su vez ser alternativamente positiva o negativa mientras que se expande gradualmente en el espacio en forma de onda. Esto podría significar que el universo puede expandirse y contraerse en un cierto intervalo de tiempo y espacio, sin llegar nunca a la muerte térmica y sin que su fase de expansión actual se tenga que explicar por una explosión original .

5. Señalamos de paso que si el electrón y el protón pueden ser considerados como esferas, entonces el electrón tendría un volumen de más de seis mil millones de veces más grandes que el protón, dado que si el electrón tiene un radio de aproximadamente 1.835,791 veces mayor la del protón , esto significa que su volumen sería 1835.791 … ³ = 6.186.859.530 veces mayor (un número que es muy, muy cerca de 1/ɸ x 1010). Tampoco podemos dejar de señalar que la constante que sirve para determinar la relación entre la fuerza gravitacional y la magnética expresada por un electrón es aproximadamente 4,17, es decir, un número que está muy cerca de la relación entre los valores constantes que se utilizan para determinar el volumen del círculo, ya que 4/3 π = 4.188… Teniendo en cuenta las dimensiones de que estamos hablando, no se puede excluir que el valor determinado por la geometría corresponda más exactamente a la realidad de lo que se determinó empíricamente. Pero esto no parece el caso , porque si hacemos la proporción entre la relación entre la fuerza magnética y la fuerza gravitacional expresada por un protón y un electrón, nos damos cuenta de que el resultado es determinado por un valor cercano a 1835.791 … elevado al cuadrado, y no al cubo

4,17 x 1042 : 1,24 x 1036 = 3.362.903,2258

Si hacemos la raíz cuadrada de este número , vemos que

√3.362.903,2258 = 1833,822…

Teniendo en cuenta los pequeños errores que hay en la determinación de las constantes podemos pensar que esta relación corresponde a 1835.791…2 . Esto podría significar que el electrón y el protón deben ser considerados como una superficie, y no como volúmenes. Esto a su vez podría significar que las modernas teorías científicas que consideran la tercera dimensión – es decir, la profundidad – como una ilusión encontrarían un fundamento más. Y este podría también ser el significado más profundo de la adopción por los Antiguos Egipcios de la representación bidimensional. Además , si hacemos la relación entre el radio clásico del electrón y el del protón excluyendo las potencias de diez obtenemos otro resultado interesante ya que

2,8179403267 : 1,535 = 1,835791…

Si hacemos la relación entre esta cantidad y la carga eléctrica del electrón y del protón , vemos que

1,835791… : 1,60217653 … = 1,145810692…

Este número parece ser extremadamente importante porque es prácticamente idéntico a 1 + 1/ɸ4. En efecto

1 + 1/ɸ4 = 1 + 0,145898.. = 1,145898…

Como se puede ver, la diferencia es de unos 8 x 10-5 (curiosamente , 8 y 5 son el sexto y el quinto número de la serie de Fibonacci y su producto nos da el 40, un número que en el Antiguo Testamento se puede encontrar continuamente: si hacemos el producto de los 40 días y de las 40 noches que dura el Diluvio Universal, tenemos 1600, un número muy cercano a ɸ multiplicado por 1.000, cuya raíz es 40,22). A esto podemos agregar los resultados que hemos encontrado anteriormente. Si excluyendo las potencias de 10 hacemos la relación inversa entre el radio del protón y el del electrón, nos encontramos con que

1,535 : 2,817940367 = 0,54472408….

Este número – elevado al cubo – es 0.161632 … , un valor esta vez muy similar a ɸ/10 (de hecho 3√(ɸ/10 ) = 3√0,1618033988 … = 0,544915…; la diferencia con el valor calculado anteriormente es de 21 diezmilésimos). En vez, multiplicado por 2 y luego elevado a la sexta potencia nos da

(0,54472408… x 2)⁶ = 1,08944817…⁶ = 1,67201227…..

Es decir, un valor notablemente similar a el de la constante que se utiliza para calcular la masa en reposo del protón, que es igual a 1,6726231. Teniendo en cuenta muy pequeños errores en la determinación del radio clásico del protón y el electrón , podemos suponer que los valores de las nuevas constantes corresponden perfectamente a 1 + 1 / ɸ4 y 3√(ɸ/10) . Este hecho puede explicar por qué los Antiguos Egipcios quisieron codificar ɸ y π en la Gran Pirámide: porque con estos dos números se puede describir la forma lógica, física y geométrico – matemática de todos los eventos que suceden en el mundo.

6. La conexión de la proporción inversa entre el radio clásico del protón y el electrón y su masa con el resto de sus propiedades físicas se completa con el descubrimiento – que ahora no es tal vez demasiado sorprendente – que esta relación parece repercutir incluso en la distancia media desde el núcleo de la primera órbita en el átomo de hidrógeno, que corresponde a 0,53 x 10-10 m. De hecho , si hacemos la relación de esta distancia con el radio clásico del electrón , vemos que

0,53 x 10-10 : 2,8179403267 x 10- 15 = 18808,0632…≈ 3/ɸ x 104

Si hacemos lo mismo con el radio clásico del protón llegamos en vez a este resultado

0,53 x 10-10 : 1,535 × 10-18 = 34527687,2964..

Si dividimos este número por lo que hemos logrado con el electrón tenemos que

34527687,29641 : 18808,0632 = 1835,791

Obviamente, encontramos una vez más el número que define la relación inversa entre el radio y la masa del protón y el electrón . Si se divide por 10 el valor relativo al protón y después hacemos la raíz

√(34527687,296… : 10) = √3452768,7296… = 1858,162729

Este número asume importancia porque parece establecer una relación entre el radio de la primera órbita y la del electrón y el protón , aludiendo a otro valor constante misterioso. De hecho , si dividimos por este valor ese relativo al electrón a su vez dividido por diez nos encontramos con esta relación

18808,0632/10 : 1858,162729 = 1880,0632 : 1858,162729 = 1,012186…

Si hacemos la proporción entre 1858,806 y la relación entre el radio del protón y el del electrón veamos que el resultado es todavía

1858,1627 : 1835,791… = 1,012186.4248…

1835,791… x 1,012186…2 = 1880,80628…

Este número (1,012186) corresponde con bastante exactitud a la proporción h medido en joule (6,625) y en erg (6,55), ya que 6,62559 : 1,012186 = 6,5458 . También sabemos que las distancias de las órbitas de los electrones del núcleo están íntimamente relacionados con su estado de energía , que está conectado a su vez con el número cuántico principal. Además, estas relaciones a base 10 entre el valor de radio clásico del protón y electrón y el radio de la órbita podría ser de alguna manera la causa de la creación de un sistema de medida métrico-decimal Antiguo Egipcio (que a su vez podría ser la causa de nuestra propia medida). Así, parece que entre el espacio y el estado de energía existe, a nivel microscópico, una íntima conexión, similar a la que la relatividad general pone entre masa y energía. Por lo tanto, la teoría del campo unificado del Antiguo Egipto sería, por así decirlo, una especie de generalización de la relatividad general en la que el espacio, entendido como la relación entre el radio clásico del electrón y el protón , entra en la definición de la masa, la carga, la distancia entre la órbitas y viceversa. Que los antiguos egipcios hubieran llegado a una concepción de este tipo es una posibilidad que hay a tener en cuenta no sólo todo por lo que hemos visto en la primera parte del artículo, sino también por estos nuevos descubrimientos. Hecho 1 el radio clásico del electrón , hemos visto que el del protón corresponde a 1/1,835.791 de esta medida. Si redondeamos este número a la cifra más alta (1836 ) y luego lo dividimos por uno de los dos números típicos del ciclo de Sirio (que eran 1460 y 1461) tenemos que

1836 : 1460 = 1,2575…

Si tomamos este resultado, lo elevamos al cuadrado y lo multiplicamos por 2, tenemos que

1,2575…2 x 2 = 3,162784762….

Este número está muy cerca de 10 multiplicado por el coseno de ese ángulo de 71°,5531…, que hemos visto más arriba, cuya tangente es igual a 2.9979246 … : o sea, prácticamente idéntica a la constante de la que podemos derivar la velocidad de la luz . Multiplicando el coseno del mismo ángulo (0.316424 … ) por la tangente y luego haciendo 1/x, se obtiene un número igual a 1,054165 …, lo que corresponde casi a la perfección a ħ, el valor con el que con frecuencia se reemplaza “h”, la constante de Plank (ħ = h/2π = 1,054571 ). Como hemos visto, un valor aún mejor aproximado lo podemos derivar sumando seno, coseno y tangente de un ángulo igual a π/2, y todo esto significa que tal vez podamos decir que hemos descubierto que entre geometría y realidad no hay ninguna diferencia sustancial. Todos esos resultados a los que nuestra ciencia ha llegado por largas y agotadoras investigaciones empíricas podrían haberse deducido de especulaciones geométricas desarrolladas de forma totalmente a priori. Quién sabe, tal vez esta es la razón porque Platón dio tanta importancia a la geometría.

7. De hecho, si tratamos de resumir y poner un poco de orden en los resultados obtenidos durante esta investigación tal vez demasiado tortuosa, vemos que por fin son bastante interesantes. En primer lugar, vemos en serie los valores de el radio clásico y la masa del electrón y del protón

masa en reposo del electrón = me = 9,1091 x 10-31 kg

masa en reposo del electrón = mp = 1,6725 x 10-27 kg

radio clásico del electrón = re = 2,81777 x 10-15 m

radio clásico del protón = rp = 1,535 × 10-18 m

Como ya hemos visto al menos en parte, las relaciones que podemos construir a partir de estos valores son muy interesantes. Y aún más interesantes nos aparecerán cuando nos daremos cuenta de que, quitadas las potencias del 10, todas se corresponden casi perfectamente a relaciones entre π y ɸ

me/re = 9,1091 : 2,81777 = 3,232733… ≈ 2ɸ

mp/rp = 1,6725 : 1,535 = 1,08957… x 10-9 ≈ (2ɸ/π)3

Pero, como hemos visto anteriormente, la relación 2ɸ/π corresponde casi perfectamente a la relación entre el número de días del año solar y de las fases de la luna, ya que 365,25 : 354,36 = 1,0307314 .. y 2ɸ/π = 1,030072: la diferencia con el valor que sale de mp/rp parece por lo tanto realmente insignificante. De hecho, vemos que, como la proporción queda casi idéntica – ya que (me/re) ≈ 2ɸ – hemos que la relación con 3√mp/rp nos da número muy cercano a π.

3√mp/rp = 3√1,08957… = 1,029009…

(me/re)/ 3√ mp/rp = 3,232733…. : 1,029009… = 3,141598…. ≈ π = 3,141592…

La diferencia con π es finalmente no mayor de aproximadamente 6 x 10- 6. En este punto , nadie se sorprenderá mucho de que incluso la constante de Bohr con la cual se calcula al radio de la primera órbita del electrón alrededor del núcleo del átomo de hidrógeno se pueda derivar con buena aproximación por una función de ɸ. El valor de esta constante es de hecho de 0,53 x 10-10 m. Podemos obtener este valor de esta manera

1/(1 + 1/ɸ3)3 = 0,5295…

Así, si la longitud de onda es λ = 2πr/n, donde “n” es la serie de los números naturales, entonces podemos obtener el valor de λ por medio de una función de π y ɸ , ya que podemos escribir

λ = 2π [1/(1 + 1/ɸ3)3]/n

8. Estas relaciones tienen consecuencias obvias con respecto a las ecuaciones que tienen relación con los valores dinámicos de partículas elementales. Por lo que hemos visto más arriba, sabemos que la masa del electrón se puede derivar de su radio con una ecuación bastante simple. Dado que

me/re = 9,1091 : 2,81777 = 3,23273… ≈ 2ɸ

de este sigue por consecuencia que

me = re 2ɸ

De esta manera, la famosa ecuación sobre la longitud de onda del electrón de Broglie

λ = h/me v

podría ser transformada así

λv = h/me = (seno π/2° + coseno π/2° + tangente π/2°) x 2π/re x 2ɸ

Pero si tenemos por 1 el radio del electrón (es decir, si lo mantenemos como una unidad de medida) la ecuación se convierte en una simple función de π y ɸ

λv = h/me = (seno π/2° + coseno π/2° + tangente π/2°) x 2π/2ɸ

Arriba hemos visto que λ = 2π [1/(1 + 1/ɸ3)3] /n. Por lo tanto , podemos transformar esta fórmula de esta manera

{2π [1/(1 + 1/ɸ3)3] /n} v = (sin π/2° + cos π/2° + tg π/2°) x 2π/2ɸ

Por consiguiente, tenemos que v es igual a

v = [(seno π/2° + coseno π/2° + tg π/2°) x 2π] : 2ɸ {2π [1/(1 + 1/ɸ3)3] /n}

O bien, el famoso principio de incertidumbre desarrollado por Heisenberg se convertiría en

Δx Δp ≥ 1/2 ħ = Δx Δp ≥ 1/2 sen π/2° + cos π/2° + tg π/2°

o bien

Δx Δp ≥ 1/2 ħ = Δx Δp ≥ 1/2 9√ɸ

Con un procedimiento de este tipo podemos derivar la constante (1,535) que necesitamos para determinar el radio del protón, y la relación (1,835791 ) que la une a la del electrón . Vamos a empezar de nuevo desde π , pero en la aproximación que encontramos en la Gran Pirámide, que corresponde a la fracción pitagórica 22/7

rp = (22/7 : 2) : {1 + [(1/ɸ3) : 10]} = (3,142857… : 2) : {1 + [1/0,618033…3] : 10]} = = 1,57142857… : [1 + (0,23606… : 10] = 1,57142857… : 1,023606… = 1,53518…

Podemos derivar la constante de la masa desde el radio clásico obteniendo el diámetro y dividiéndolo por la constante (1,835791) que establece que la masa es inversamente proporcional a las dimensiones del radio

dp = (rp x 2) = 1,535 x 2 = 3,07

dp : 1,835791 = 3,07 : 1,835791 = 1,6725 mp

La carga se puede derivar dividendo la misma constante (1,835791) por 1 + 1/ɸ4

1,835791 : (1 + 1/ɸ4) = 1,835791 : 1,145898… = 1,6020….

Dos maneras posibles para derivar la constante igual a 1.835791 son los que ven a continuación

3√(1/ɸ x 1010) : 103 = 1,835146..

O bien, utilizando una aproximación muy exacta de π (3,1438 , que difiere del valor real de π menos de 3 milésimos) podemos escribir

103,1438 + (103,1438/3,1438) = 1392,51… + 442,94… = 1835,45…

Con el valor real de π esta misma ecuación nos da el valor siguiente

10π + 10π/π = 1385,455 + 441,004 = 1826,45998

También parece bastante significativo que el valor de la relación entre el radio del protón y el del electrón da un resultado muy interesante si lo relacionamos con el ángulo redondo y por lo tanto también con el número de días “puros” del calendario solar Maya y Antiguo Egipcio

1835,791 : 360 = 5,0994 ≈ πKeops x ɸKeops = (3,142857 x 1,61859) = 5,0869969

1835,791 : 3602 = 0,014165… ≈ (π – 3) : 10 = 0,014159…

O, de una manera más simple pero más aproximada, podemos derivar este número que con esta fórmula

ɸ2/π + 1 = 1,8333461…

Esta cifra – que es un poco inexacta en cuanto a la ley que regula la relación inversa entre la masa y el radio en el protón y el electrón – pero es casi perfecta para definir la relación entre la fuerza magnética (Fme y Fmp) y aquella gravitacional (Fgp y Fge) expresadas por un protón y un electrón. Para mayor comodidad vemos de nuevo los cálculos que hemos hecho anteriormente

Fmp/Fgp = 4,17 x 1042

Fme/ Fge = 1,24 x 1036

4,17 x 1042 : 1,24 x 1036 = 3.362.903,2258

Haciendo la raíz cuadrada de este número hemos visto que

√3.362.903,2258 = 1833,822…

Un número que corresponde de una manera que parece muy significativa a lo que hemos visto anteriormente (ɸ2/π + 1 = 1,8333461… ). Dejamos por última esta que podría ser más que una curiosidad, porque efectivamente este número puede ser obtenido también a partir desde el número de partículas elementales conocidas para los Dogon – 266 – ya que 266 x (2π + 1/ɸ) = 266 x 6,901219… = 1835,724. Sea lo que sea, incluso olvidándose este ultima extrañeza arqueológico-científica, ahora sabemos que a partir de las ecuaciones que hemos visto hasta ahora , podemos convertir todas las ecuaciones de la “viejos” la mecánica cuántica en funciones ɸ y π . Y proprio esto, funciones matemáticas de ɸ y de π, podrían ser los que Platón llamó ” elementos “. Como en su pensamiento – al igual que en el del Antiguo Egipto – no había ninguna diferencia entre la teoría y la abstracta realidad geométrica-matemática , una función matemática podría muy bien significar un elemento de la realidad microscópica, o un ciclo cósmico, etc.

9. Sin embargo , vamos a profundizar este tema en un trabajo posterior, ya que en estas relaciones – por inverosímil que parezca – puede ocultarse el punto de partida para comprender la teoría del campo unificado que los Antiguos Egipcios habían probablemente ya logrado al momento de la construcción de las Pirámides de la llamada IV Dinastía.En esta teoría, el campo gravitacional sería la consecuencia de una particular distribución espacial del campo magnético; o , viceversa, ya que las medidas están conectadas por medio del radio, el campo magnético sería el resultado de una distribución particular en el espacio del campo gravitacional (y por tanto de la masa). Esta no es – en sentido absoluto – una novedad, dado que la teoría de la relatividad ya nos advirtió que la energía puede ser pensada como un estado de la materia, y la materia como un estado de energía. De esta manera podemos también explicar el origen del monofisismo como teoría religiosa : si estas suposiciones corresponden la realidad, entonces cada entidad es sí misma y también todas las otras, y por fin todas son Uno. En un ámbito como este el espacio en sí mismo debería ser considerado como una fuerza: así cambiaria completamente el significado del valor de d² en una fórmula como la de Newton. Este valor no se debería entender como el efecto de una entidad amorfa y pasiva (precisamente, la distancia), sino como un principio activo de una fuerza que se opone a los efectos de la masa sobre la otra masa, y por lo tanto como una especie de fuerza de la gravedad de signo opuesto. Esto nos puede sorprender en este momento y incluso nos parecer totalmente incomprensible. Pero en realidad esta manera de concebir la realidad física no es más que la teoría de la relatividad llevada a su conclusiones extremas: de hecho, si la masa puede tener un efecto en el espacio-tiempo, porque el espacio-tiempo no podría tener un efecto en la masa ? Para concluir con este tema, podemos decir que en un trabajo posterior vamos a demostrar que la relación entre el metro de la Gran Pirámide y lo que actualmente está en uso en Occidente es casi idéntico a lo que existe entre G y h . De esta manera también demostraremos que los Antiguos Egipcios poseían ambas estas unidades, así como el codo , el medio codo, etc ( La fuente de todas sus unidades de medida de longitud parece ser un milímetro igual a 1,0066 de nuestros milímetros ) . Recordemos que la carga magnética de un electrón expresa una fuerza igual a 4,17 x 1042 en comparación con la de su campo gravitatorio, y que su masa es igual a aproximadamente 1/1835,791 la del protón . Tomando x = 4,17/1836, y luego haciendo 1/x obtenemos … 440,28 , que a un nivel numerológico corresponde casi perfectamente a la longitud de un lado de la Gran Pirámide expresada en codos. Parece también bastante notable que podemos obtener una buena aproximación al valor de esta constante siguiendo un camino cosmológico, haciendo la raíz cúbica de la duración de un Día Precessional medido en años solares, ya que 3√72,2222 = 4,16444 . Si en vez dividimos 1835,791 por uno de los dos números típicos del ciclo de Sirius, luego lo elevamos al cuadrado y por fin multiplicamos el resultado por 2, vemos que 1835,791 : 1460 = 1,25653… 2 x 2 = 3.162064736 … , un número casi idéntico a √10 = 3.162277 y por lo tanto muy similar, como ya hemos visto, al producto de ħ por la constante que necesitamos para obtener la velocidad de la luz.

10. La investigación científica que tenemos que hacer para entender el significado de la Gran Pirámide es, por lo tanto, de este tipo. Podemos asumir que va a ser mucho , mucho más difícil de lo que cabría esperar de una cultura cuya nuestra arqueología oficial atribuye una matemática y una astronomía a nivel de nuestras escuelas primarias (o un poco más), sobre todo si tenemos en cuenta que ya los resultados de esta investigación nos empujan a enfrentarnos con problemas que hasta ahora han sido completamente inimaginables. En el libro de Graham Hancock “La Muestra y el sello: La búsqueda del arca perdida del pacto” (Capítulo Seis, p. 128 ), se cuenta un hecho aparentemente insignificante . A mediados del siglo XIX , un delegado del Patriarca de Armenia había visitado Abisinia. Su intención era la de desmentir que en todo el país estaban convencidos de que el Arca de la Alianza había sido transportada a Axum y que aún se conservaba allí. Después de un largo interrogatorio de los sacerdotes axumitas el delegado – cuyo nombre era Dimotheos – logró convencerlos a mostrar una tabla de mármol rojizo, de 24 cm de largo, 22 de ancho y 3 de espesor. Los sacerdotes le dijeron que esta era una de las dos tablas de piedra contenidas en el Arca. El volumen total de estas dos tablas es de 3168 cm³. Si dividimos esta cifra por 10000, como resultado tenemos 0.3168 que es el coseno de un ángulo muy cerca de lo que tiene por tangente la constante de que se calcula la velocidad de la luz (71°,5304 , que corresponde a una tangente de 2,9939784 ). Si lo dividimos por 3000 tenemos 1.056 , un número bastante cerca de ħ. Para que las medidas concuerden perfectamente con las que pueden darnos las constantes de nuestras leyes físicas más importantes es suficiente imaginar que las medidas de las tablas di mármol hayan sido tomadas con una muy pequeña imprecisión (se tenga en cuenta que el producto de la constante de que calculamos la velocidad de la luz multiplicada por ħ es 2.9979246 x 1.054571 = 3.1615243, que dividido por 10 da el coseno de un ángulo igual a 71°,5696; éste número – y por lo tanto también ello que se puede obtener numerológicamente desde el volumen del Arca – multiplicado por 2 corresponde con muy buena aproximación a la constante de la cual se puede derivar la constante de Newton a partir de ħ (la formula es 2 x 3,1626501… x ħ).

11. Según el Antiguo Testamento, el Arca que contenía las tablas mide 2,5 codos de largo y 1,5 codos de ancho y de altura. Ya de esta manera estas medidas parecen muy significativas. La longitud dividida por el ancho da un resultado de 1,6666 … , un número muy cercano del número de oro ( 1,618033988 … ) e idéntico a la constante que se utiliza para transformar los sesentavos de un grado en centésimos de grado. Pero es probable que estas medidas fueran transcriptas de manera un poco inexacta, para no transgredir un secreto hermético, representado por medidas mucho más significativas. Se puede especular, por tanto, que el Arca tenía una longitud de 2,618033988 … codos (ɸ²), y una anchura y una altura de 1,618033988 … codos (ɸ) . Tenemos que recordar que ɸ / π = 0,515036: numerológicamente esta cifra es muy similar a la inclinación de la pirámide de Keops , que, medida en grados y sesentavos de un grado, es de aproximadamente 51° 51′, y que 2ϕ : √(√(√(√ϕ) = 3,14018. Sin embargo, incluso en esta forma las medidas del Arca tienen claras alusiones tanto a ɸ que a π. Si suponemos que la unidad de medida fuera 0,5 codos, sigue que la longitud del Arca es igual a 5 veces esta unidad, y la anchura y la altura a 3 veces. Así que podemos construir esta proporción, caracterizada por 3 y 5 (que, hay que recordar, son el cuarto y el quinto número de la serie de Fibonacci): (2.5 x 1.5 x 0.5) : 3 = 0,625 (1/ɸ = 0 , 618033988 … ); Este número, multiplicado por 5 nos da 3.125, un número muy cercano a la aproximación de π que encontramos en el sarcófago de Djedefre ( 3,12179 … pero vamos a ver el argumento en la sección 7 de El Código de Snefru 7; de todos modos, la tangente de un ángulo de 3°,125 es igual a 0,054595 … , un valor casi idéntico a h – 1). Los 2,5 codos de largo son significativos en comparación al ángulo de 360° (y, por tanto, también en comparación con los días “puros” del calendario solar egipcio antiguo) ya que 360 2,5 = 144, un número que corresponde a 2 Días Procesionales redondeados a la cifra entera (72 x 2 = 144) y también al 12° número de la serie de Fibonacci. La raíz de 144 nos da de nuevo 12, el número de meses del calendario solar Antiguo Egipcio (debemos notar que estas relaciones de númerologícas, que para nosotros no son nada, en la antigüedad se sentían casi como las notas de la divina armonía, que era considerada la ley secreta del universo). El ciclo de Sirio , dividido dos veces por la constante con la cual se calcula la velocidad de la luz y luego por 100 da un resultado igual a 1461 : ( 2 x 2,9979246 ) : 100 = 1.625 …; es fácil por lo tanto que lo que se llama “Arca de la Alianza”, fue la estrella Sirio y los números asociados con su ciclo, que a su vez contenían los números de esos conocimientos físicos fundamentales que dan al hombre el poder sobre la naturaleza (a su vez, las historias que hablan del Arca que va desde Egipto a Israel, y luego desde Israel a Etiopía, no parecen más que una manera hermética de aludir a observaciones astronómicas que son posibles antes en un lugar y luego en otro). Esta hipótesis se ve reforzada por el hecho de que en el pasado en el cristianismo se ha hecho referencia a la Virgen María como al Arca de la Alianza. Y los vínculos entre la figura de la Virgen y la de Isis están claras desde el Apocalipsis. Entre muchas otras cosas que podríamos citar para comprobar este hecho histórico, parece muy significativo que se haya encontrado en Egipto una figura que representa a Isis con los pies sobre la Luna y coronada con 12 estrellas, exactamente como la mujer perseguida por el dragón de que habla el Apocalipsis (es fácil imaginar que el dragón podría ser Seth). De esa manera, se seria explicado el motivo porque Flegetanis, un personaje del Parsifal de Wolfram von Eschenbach, «veía secretos escondidos en las constelaciones (y) declaró que hay una cosa llamada Graal de la que leía distintamente el nombre en las estrellas».

12. Los lazos entre la cultura judía y el Antiguo Egipto fueron hasta ahora ignorados o subestimados radicalmente . Por tanto, es muy útil en este contexto recordar que de acuerdo a la ley judía se considera judío quien sea nacido de una madre judía. Pero debemos señalar que la esposa de Abraham era estéril (después Dios le otorgó milagrosamente un hijo a la edad de noventa años). Así, la primera Eva del pueblo judío, fue una sierva de su esposa, que era egipcia. Así que, si seguimos el testimonio del Antiguo Testamento, debemos pensar que el pueblo egipcio y el judío son muy estrictamente relacionados , como los descendientes de Abraham, siguiendo la idea matrilineal de consanguinidad, son por la mitad de sangre egipcia. Así que no es de extrañar que incluso en los números relacionados con el Diluvio y el Arca de Noé, hay probablemente alusiones herméticas a la antigua sabiduría egipcia que puede haber sido absorbida por el pueblo judío a través de la mediación de Moisés, que de acuerdo con la tradición bíblica fue adoptado por la hija del Faraón y criado como un noble egipcio. Tomamos, por ejemplo, los números asociados con las fechas

17° día del 2° mes
17° día del 7° mes
1° día del 10° mes
1° día del 1° mes
27° día del 2° mes

Si se hace la sumatoria, vemos que por los números referidos a los meses el resultado es 2 + 7 + 10 + 1 + 2 = 22, y por aquellos referidos a los días es 17 + 17 + 1 + 1 + 27 = 63. Si se hace el producto se consigue un número aparentemente insignificante, 63 x 22 = 1386 . Pero si hacemos la relación con el número típico del ciclo de Sirio vemos que 1461: 1386 = 1.054112554112554 , es decir una vez más un valor muy cerca de ħ, que se calcula igual a 1.054571. Un número muy similar resulta incluso en el Timeo, cuando Platón indica el intervalo armónico mínimo utilizado por el Creador para generar el mundo, que es de 256 : 247 = 1,053497. Este número sale incluso por la relación entre el número de días en un año solar y el llamado “año del eclipse”, ya que 365.25 : 346.6 = 1,053808 . Un número similar también sale haciendo la raíz (346,6 : π ) de 346,6, ya que 346,6 : π√346,6 = 110,32…√346,6 = 1,05448. También parece notable el hecho que [(346,6 : 100) : e]2 = 1,625…, un número que nos lleva de nuevo a las medidas del Arca. E incluso en la Gran Pirámide encontramos algo parecido. Si tenemos en cuenta que sus medidas en codos se pueden derivar de la cantidad de días puros del año solar (360) mediante la adición o sustracción de 80, podemos construir la relación (360 : 280 : (440 : 360) = 1,051948 … (que corresponde más o menos a π/3). Podemos obtener un número muy similar a este usando uno de los que son típicos del ciclo de Sirio , desde 1460 : 10√1460 = 146√1460 = 1,05117 (tomamos nota de paso que la altura de la Gran Pirámide en metros es igual a 146,56 : dividiendo por 10 el número de ciclo típico de Sirius inmediatamente se percibe la conexión numerológica entre 146,5 y 146 o 146,1; parece también considerable el hecho que al dividir el número típico de Sirius por la mitad del perímetro de la Gran Pirámide se llega a (1461: 880 ) = 1.6602 : el mismo resultado que se puede conseguir al dividirlo por la altura y luego por π, ya que (1461: 280 ) : π = 1,6608). Un resultado aún más interesante se puede obtener dividiendo el otro número típico del ciclo de Sirius, el 1460, por la altura de la pirámide de Khefren, ya que 1460 = 143,5 ≈ 2ɸπ = 10,1742 … 10,1664. Dividiendo el número de días de un año de fases lunares por el mismo número se obtiene 354,36 : 143,5 = 2,4694 ≈ (π/2)2 = 2,4674. Haciendo lo mismo con la duración del año solar obtenemos 365,25 : 143,5 = 2,5452 … ≈ πɸ/2 = 2,5416. Usando el número de los días “puros” en el año solar podemos conseguir 360 : 143.5 = 2,5087 ≈ (3,16/2)2. Ni siquiera podemos olvidar el hecho que el ciclo de Sirius – dividido por el número de días de un “Año de las Eclipses” – nos da un resultado todavía mucho interesante, ya que 1461 : 346,6 = 4,2152… ≈ ɸ3 = 4,23606 (3√4,2152 = 1,61537). En vez, dividido por un año de fases lunares, el resultado es igual a 1460 : 354,36 = 4,1201 ≈ (ɸ2/2) x π = 4,1123. Con nuestra investigación parece que somos llegados al punto de entender el significado de esas extrañas leyendas que circulan en torno al Arca de la Alianza. Si esta contiene simbólicamente, por ejemplo, los secretos científicos sobre la luz y la radiactividad, aquí estaría la explicación del motivo porque Moisés tiene una cara intolerablemente brillante cuando desciende desde el Monte Sinaí – donde la Arca fue recibida directamente del Señor. Esta no sería la descripción de un hecho real, sino una alusión mítica a la sabiduría científica que se encuentra codificada en las medidas y por lo tanto en los números que definen el Arca. Como hemos visto más arriba, una placa de hierro ordinario puede contener en código los fundamentos de la ciencia y, por tanto, de sus poderes, de otro modo inconcebibles . Esto significa que a derribar los muros de Jericó no habría sido la propia Arca, sino el poder que desde la ciencia contenida en ella fue derivado, que pero en la historia se atribuye simbólicamente al Arca. Una cosa un poco extraña, pero comprensible : es un poco como si nosotros dijéramos que fue Einstein a destruir Hiroshima y Nagasaki, o que es él que hace funcionar las plantas de energía nuclear . Tomadas literalmente, estas descripciones son ciertamente engañosas. Sin embargo, en un sentido moral o simbólico estas son sin duda verdades. Después de todo, el propio Einstein se sintió directamente responsable por el poder destructivo que se derivó de su teoría.

13. En conclusión, podemos decir que ese maravilloso y casi milagroso sistema de congruencias físico-astronómicas y metrológico -trigonométricas que encontramos en estas páginas no puede ser el resultado de una coincidencia. Que exista un sistema decimal en el que 130√103 tiene como resultado la constante fundamental de la mecánica cuántica, que es a su vez codificada en la esquina correspondiente a la división entre el exponente de la raíz y el de la potencia, ángulo que a su vez corresponde a uno de los que se encuentran en el rango de variación de la inclinación del eje polar de la tierra en relación con la eclíptica no puede ser absolutamente un caso. Es suficiente adoptar una trigonometría en la que el ángulo redondo se divide en cualquier número de partes diferentes de 360, o una diferente metrología e inmediatamente este sistema de correspondencias se destruye. Esto significa que el sistema métrico actualmente en uso y todo lo que vino como resultado de eso en los varios campos de la ciencia empírica es una herencia que nos llegó a través de tradiciones herméticas desde la profundidades insondables del tiempo en que se inventó este sistema numérico, construido para llegar a una armonía milagrosa de trigonometría pura, física clásica y cuántica y los ciclos específicos de la Tierra, que también tienen profundas relaciones númerologícas con los ciclos de los otros planetas del sistema solar. Ni siquiera podemos excluir que en un pasado muy lejano viajeros procedentes de las profundidades del espacio han optado por establecerse en este planeta porque era el único – o, al menos, el primero que encontraron – en que los números de la física y de la geometría coincidían con los de los ciclos cósmicos. Ninguna hipótesis ahora es arriesgada, dada la imposibilidad de que lo que hemos visto en estas páginas se pueda atribuir a la casualidad. A partir de entonces, estudiando la geometría de tradición pitagórica, debemos preguntarnos: ¿quién fue capaz de desarrollar un sistema abstracto que puede coincidir con tanta meticulosa exactitud con las magnitudes detectadas por la física microscópica? De hecho, si la suma de tangente, seno y coseno de un ángulo igual a π/2 corresponde a ħ; si haciendo 1/x con x igual al coseno de un ángulo cuyo seno es igual a 1/π (es el ángulo de 18°,56…) , nos encontramos de nuevo ħ; si elevando al cuadrado la suma de seno y coseno de ese mismo ángulo nos encontramos con un valor muy cercano a la carga elemental ; si con la adición de seno y coseno y tangente de ese ángulo se encuentra el valor de la carga elemental “en persona”, ¿cómo podemos siquiera atrevernos a imaginar que este es un sistema de coincidencias ? ¿Cómo pueden las coincidencias formar un sistema ? El sistema es siempre obra de la inteligencia ! En un ángulo igual a 20 x ɸ = 32°, 36… la suma de seno y coseno es 1,3799 … , que es muy cerca a 1 + 1/ɸ2 = 1,381966 . En un ángulo de 10 x π = 31,41592 … la tangente es igual a 0,61078…, es decir una vez más a una muy buena aproximación de 1/ɸ. ¿Cómo puede alguien creer que esto es un milagro de la casualidad ? Por el contrario , aquí parece de poder constatar – a través de estos ejemplos y a través de todos los otros que ya hemos hecho y que podríamos hacer – que la trigonometría pitagórica misteriosamente gira alrededor de π y ɸ, y, para que esto suceda , debemos pensar que quien la construyó se dio cuenta de que la realidad misma gira alrededor de estos números . Este hallazgo parece demostrar de manera inequívoca que el hombre – si de algo origina – ciertamente no es del mono. Que la sabiduría que ha desarrollado esta maravilla tiene sus raíces en abismos de tiempo y, quizás, de espacio de que no podemos imaginar ni siquiera vagamente la profundidad es ahora fuera de toda duda. Tal vez el destino final de esta nuestra civilización agonizante , el destino final se deja a los que ahora se quedan sin un destino, es descubrir la tierra donde estas raíces hunden. Y es bueno darse prisa, porque el tiempo que nos queda no es mucho.

APÉNDICE 2: LA TERNA PITAGÓRICA OBTENIDA POR LOS NÚMEROS TÍPICOS DEL SISTEMA DE CALENDARIO MAYA HAAB’ – TZOLKIN EN COMPARACIÓN CON LA PLACA DE METAL QUE SE ENCUENTRA AL FINAL DEL POZO DE VENTILACION AL SUR DE LA CÁMARA DEL REY.

Los números típicos del sistema del calendario maya Haab’ – Tzolkin son, como se sabe, el 18 y el 13. A partir de estos números, como da cualquier par de enteros, podemos derivar una terna pitagórica, que corresponde a un triángulo que en este caso tiene las siguientes medidas

13² + 18² = 169 + 324 = 493 HIPOTENUSA

18² – 13² = 324 -169 = 155 CATETO MINOR

2 x 13 x 18 = 468 CATETO MAYOR

sin α = 155 : 493 = 0,314401…: tenemos en cuenta que este valor corresponde casi a la perfección a π/10 = 0,314159…

ángulo α = 18°,324694

ángulo β = 71°,675305 tenemos en cuenta que la suma de seno, coseno Y tangente de este ángulo es igual a 4,28304 , mientras que 2π – 2 = 4,28318 .

(seno α + coseno α)2 = 1,26369…2 = 1,5969… Si de esta cifra se sustrae 1 obtenemos 0,596916 … , un número notablemente similar al resultado de la relación entre la constante del momento magnético del protón 2,793 y la de su masa en reposo , ya que 1,6726231 : 2793 = 0,598862

Tangente del ángulo β 71°,675305 = 3,019354 …

La tangente del ángulo opuesto al cateto mayor de la placa de metal que se halló al termino del pozo de ventilación Sur de la Cámara del Rey – que corresponde a un ángulo de 71°,55315 – era igual a 2,9979246 . La diferencia entre los dos valores es de 0,0214.

La relación entre la hipotenusa y el cateto más grande del “triángulo Maya” es 493 : 468 = 1,0534188… ; esta misma relación, en el caso del plato de metal Antiguo Egipto, era igual a 1,05416554, con una diferencia de – 0,00074674. La diferencia con el valor exacto de ħ (1.054599) es igual – 0,001180196, que es un poco más de 11 diez milésimas . Un número similar también sale en el Timeo , cuando Platón indica el intervalo armónico mínimo utilizado por el Creador para generar el mundo, que es de 256 : 243 = 1,053497. En este caso la diferencia es de – 0,0000782.

Además, se puede obtener una muy buena aproximación a ħ con una simple elaboración matemática del ángulo que tiene un seno igual a 1/π . Este ángulo es de 18°,560744 , y su coseno resulta 0,947986717 … .; haciendo 1 /0,947986717 obtenemos 1,054867, diferente de ħ “en persona” de menos de 3 milésimos. Y ya hemos visto que un ángulo muy próximo a 18°,560744 es el más pequeño del triángulo rectángulo que resulta de la terna pitagórica que podemos obtener a partir del 18 y 13. Y, la suma del seno, el coseno y la tangente de este mismo ángulo nos da la figura de la carga elemental, dado que 0,3357746… + 0,9479867… + 0,3183098 … = 1.602 Otro ciclo muy importante para los Mayas era el de Venus. En el primer caso, podemos ver que Venus hace 13 revoluciones alrededor del Sol en el mismo tiempo en que la Tierra hace 8 de ellas. Esta relación sigue del hecho de que mientras que la Tierra emplea 365,25 días para hacer una vuelta, Venus emplea sólo 225 días, lo que significa que la relación entre estos ciclos es igual a 365,25 : 225 = 1,62333 … , es decir, un número muy similar a lo que sale de los dos términos sucesivos de la serie de Fibonacci 13 y 8 (13 : 8 = 1,625). Esto nos lleva a la misma relación que sale del ciclo de Sirio dividido por 2 veces la constante que produce la velocidad de la luz y luego por 100. Como hemos visto, 1461 : ( 2,9979246 ) : 100 = 1.625. Este número tiene también una relación numerológica con las medidas del Arca, que se caracterizan por una proporción de 0,625. Poniendo en relación el ciclo de Sirio con lo de Venus obtenemos de nuevo el mismo número, ya que (1461 : 225 ) : 4 = 1,623333. Tomando como punto de referencia la Tierra, el ciclo de Venus aparece en una forma completamente diferente. De hecho, el planeta desaparece en el crepúsculo, para reaparecer luego 8 días después por la mañana justo antes del amanecer. Después de 263 días (aproximadamente 9 meses) de vagar por el cielo se acerca al sol y desaparece de nuevo, siendo aparentemente ausente durante unos 50 días, ya que pasa por detrás del Sol. Entonces se hace visible de nuevo durante otros 9 meses más o menos (anotamos de paso que el 50 es el número típico del ciclo de Sirio B alrededor de Sirio A, que sigue siendo muy importante para los Dogon, una cultura una vez vinculada a los Antiguos Egipcios). Durante este período , su brillo aumenta hasta que alcanza el máximo. Venus completa este ciclo en 584 días, un número que los Mayas habían registrado con exactitud y que para ellos era naturalmente muy sagrado. En el primer caso, podemos ver que 584 ≈ ( 2ɸ2 + 1/ɸ) x 102 = 585,41, al igual que los dos medios ciclos de 263 días están muy cerca de ɸ2 x 102 = 261,8. Es natural observar aquí que los dos números típicos del calendario Tzolkin también están conectados a ɸ2, ya que los 260 días del total de un ciclo es más o menos igual a ɸ2 x 102 = 261,8, mientras que una fracción de 13 días es más o menos igual a ɸ2 x 5 = 13.090. Si hacemos la relación entre la duración del ciclo de Venus observado desde el punto de vista del Sol (225 días) y lo que observamos desde el punto de vista de la Tierra vemos que el resultado tiene de nuevo que ver con el número de oro, ya que 584 : 225 = 2,59555 , una serie de nuevo muy similar a ɸ2 = 2,618033988.

En relación con el ciclo de Sirio vemos que este número también asume razones de interés, dado que – si se tiene en cuenta el segundo número típico del ciclo, el 1460 – vemos que la relación es igual a 1460 : 584 = 2.5, es decir la longitud del Arca en codo. Pero ya hemos visto que 2,5 es una cifra muy significativa en comparación a un ángulo redondo como con los días “puro” del calendario solar Antiguo Egipcio, ya 360 : 2,5 = 144, un número que corresponde a 2 Días Precessionales redondeados al número entero (72 x 2 = 144) y también al número 12 de la serie de Fibonacci, que es justamente el 144. La raíz de este número nos da de nuevo el 12, el número de meses del calendario Antiguo Egipcio. Además , como hemos visto en abundancia, el 144 es un número que tiene profundamente que ver con las constantes de la física de las partículas. En este contexto parece particularmente importante observar como 584 x π = 1834,69, es decir un número muy cerca de la constante che determina la relación inversa entre el radio clásico y la masa que parece caracterizar protón y electrón (el valor exacto de esta relación resultaba 1835,791).

Eran muy importantes para los Mayas también los movimientos periódicos de Marte, y registraron con precisión sus etapas de “movimiento retrógrado”, esas en que el planeta, superado por la Tierra en su órbita alrededor del Sol, parece alejarse en su parábola a lo largo de la eclíptica. El número de días que transcurre entre las mitades de dos períodos retrógrados es 780, un número que, como se puede ver inmediatamente, corresponde exactamente a la duración de 3 periodos Tzolkin de 260 días cada uno. Este ciclo particular de Marte, visto en relación con el sistema de Sirio, nos permite encontrar de nuevo una característica de la Arca, ya que (1461 : 780) : 2,9979246 = 0,624791, que es más o menos la proporción de 0,625 que surge desde la relación entre las medidas del Arca. En vez, multiplicado por 4 y dividido por 103 , este ciclo de Marte nos lleva de nuevo al número típico de sarcófago de Djedefre, el 234 , que, analizado en relación con el ciclo de Sirio, nos dio una aproximación a π que fue muy interesante durante la investigación, ya que tiene importancia en relación con la física, en particular, con la constante gravitacional G. En efecto (1461 : 234) : 2 = 3,1217… , mientras que (780 x 4) : 103 = 3,12, al cual corresponde la tangente de un ángulo de 72,2286, que numerológicamente es casi idéntico a la duración del Día Precessional, con todas sus conexiones con las constantes de la física que ya hemos visto. Dividiendo el 780 por el 234 tenemos de nuevo un número característico , el 3,333 … , que multiplicado por 2 nos recuerda el “número de la bestia”, el bíblico 666 , y también el ángulo de 54 grados (360 : 54 = 6,6666…) , que numerológicamente corresponde a tres cuartos de un Día Precessional . También parece notable su congruencia con el seno de 138°, 19 que es igual a 0,6666625 (138°, 19 es el ángulo del icosaedro, el más característico de los sólidos platónicos , que se puede derivar también a partir del número de oro con esta fórmula [1 + (1 / ɸ2)] x 102 = 138,1966). En cambio, dividiendo el 780 por un “Año del Eclipses” conseguimos 780 : 346,6 = 2,25043 … . Si después dividimos los 360 días “puros” del calendario solar Haab’ con este número redondeado a 2,25 y elevado a la quinta potencia, retornamos una vez más a la aproximación de π que nos encontramos al relacionar el número característico del sarcófago de Djedefre con el ciclo de Sirio, dado que 360 : 2,255 = 6,2429…, y 6,2429 : 2 = 3.1214 …

Los primeros cinco libros del Antiguo Testamento han sido escritos segundo un código por el cual le 5 letras de la palabra “torah” están escandidas siguiendo un orden basado en 50. Por ejemplo, si a un cierto punto encontramos una “t”, contando 50 letras se encontrará una “o” y después otras 50 una “r”, etc. Y está claro que el 50 resulta una cifra numerológicamente conectada con otras cifras importantes. Dividiendo el número de los días “puros” del calendario solar Antiguo Egipcio por 50 tenemos que 360 : 50 = 7,2, una clara alusión numerológica al 72. A su vez, 72 : 50 = 1,444…, que obviamente alude al 144. El número del sarcófago de Djedefre lo podemos encontrar de nuevo por medio del 50 y del 40. Si ponemos x = 50 : 40 = 1,25 y después hacemos x : 1/x tenemos que 1,25 : (1 : 1,25) = 1,5625. Una optima aproximación a πDjedefre sale también de 1,5625 x 2 = 3,125.

Tomando en consideración el Nuevo Testamento, vemos que Jesús nos dice que tenemos que perdonar no por 7, sino por 70 veces 7. Esto quiere decir que tenemos que perdonar por 490 veces. Si dividimos este nombre por 360 llegamos a 490 : 360 = 1,36111…, una cifra muy cerca a e/2 = 2,71828…/2 = 1,35914…

Si dividimos el ciclo de Sirius por esto mismo número, después por π, y por fin hacemos 1/x tenemos que 1 : [(1460 : 490) : π] = 1,054370, es decir una aproximación de ħ muy cerca a ella que hemos ya encontrado en el plato de hierro hallado por Vyse en la Gran Pirámide.

Muy interesante, a un nivel numerológico, es también la duración del ciclo de retrogradación de los nodos de la luna, que corresponde a 18,61 años solares. Si lo dividimos por 3 tenemos que 18,61 : 3 = 6.20333 … ≈ 1/ɸ x 10 = 6.18033. En cambio, elevado al cuadrado, este número nos da la duración de un “Año de Eclipse” que corresponde a 346,6 días. De hecho, 18,612 = 346,33 ≈ 346,6. También parece notable que se pueda obtener el número de días en el año del eclipse con la fórmula (π x √5)3 = 7,0248…3 = 346,66. Los 18,61 años solares corresponden a 6793 días. Dividiendo por ɸ8 este número obtenemos una buena aproximación de la duración en años solares de dos Días Precessionales (144,444…) ya que 6793 : ɸ8 = 6793 : 46,9787 … = 144.59. En vez, dividido por ɸ16 este número nos da 6793 : ɸ16 = 6793 : 2206.999 … = 3.077, una cifra muy cercana a la constante que necesitamos para calcular el diámetro clásico del protón que, como hemos visto, es igual a 3,07.

Los Mayas tenían también un calendario que fue utilizado para el cálculo de cantidades de tiempo muy grandes, que fue llamado “Cuenta Larga”. La unidad de tiempo más largo era el “kinchiltun”, que incluye 1.152.000.000 días. Esta unidad de tiempo parece tener algo que ver con ese misterioso número, el 888, que se obtiene de la relación de las principales medidas de la Gran Pirámide expresas en codos y en metros. De hecho este número , dividido por 360, nos da un resultado numerológicamente idéntico, como 1152000000 : 3602 = 8888,8888…. Este mismo número, si se divide por el número de días de un ciclo de Sirio, nos da una muy buena aproximación numerológica a un Mes Precessional calculado en 26.000 : 12 = 2,1666… años solares. De hecho, 1152000000 : (1460 x 365.25) = 1152000000 : 533265 = 2160,27.

A un nivel numerológico también vale señalar que Júpiter gira alrededor del Sol cada 4332,667 días terrestres. Si dividimos esta cifra por el número de días “puros” de un año solar Maya o Antiguo Egipto vemos que 4332,667 : 360 = 12,035. Un año “puro ” en la Tierra , por lo tanto, corresponde casi exactamente a un mes a Júpiter, ya que 360 días terrestres son 1/12 del tiempo que emplea en completar una revolución alrededor del Sol.

En cuanto a Saturno, el tiempo de una vuelta alrededor del Sol es igual a 29,458 años de la Tierra: por lo tanto, hay una correspondencia numerológica casi perfecta entre esta cifra y la longitud de un mes sinódico lunar igual a 29,5306 días solares. Y, de hecho, al dividir el número de días de la revolución de Saturno alrededor del Sol con la duración del mes lunar tenemos que (29,458 x 365,25 ) : 29,5306 = 364,35 , cifra muy cercana al número de días de un año solar entero. Es posible que este tipo de relación podría haber llevado a los sacerdotes-astrónomos de la antigüedad a asociar la acción astrológica de la Luna a esa de Saturno.

APÉNDICE 3: TROIS POÈMES POUR S.

INTERLUDE

Ah ! cette vie de mon enfance, la grande route par tous les temps, sobre surnaturellement, plus désintéressé que le meilleur des mendiants, fier de n’avoir ni pays, ni amis, quelle sottise c’était. – Et je m’en aperçois seulement !
A. Rimbaud

Varsovie

Varsovie couverte de neige
et d’invisibles fleurs
qui des blancheurs illimitées
de la neige se nourrissent
et resplendissent
émerveillées.

Varsovie du ghetto,
du carnage.
Varsovie mille fois balayée
et mille fois
comme moi
ressuscitée.

Varsovie ta patrie
ton ciel.
Varsovie dans tes yeux
dans mon amour
comme un voile.

Varsovie de ton rire d’argent
et de ces intimes souffrances
dont je ne souffre plus
qui presque sont oubli.
Varsovie des pas qui retentissent
dans le silence de spectres d’une rue latérale,
d’une vie quelconque qui passe
fatiguée de tristesse
et dont après personne
ne saura rien.

Varsovie encore en vie
pourtant
sous en déluge de temps
qui jamais ne se retient.

Varsovie
qui s’éloigne
comme une vallée dans une évanescence
de brume sans destin,
vague labyrinthe
où le cœur
s’égare,
cherchant sens cesse ce qui reste
d’une perdue et splendide
douleur.

Varsovie,
je le sais,
désormais presque seul en nom
qui dans le ténu s’évanouir de la mémoire
s’évanouit et s’attenue
comme ton visage
dans une pénombre d’une tonnelle en été,
fixant un coin obscur,
là où je voudrais
rencontrer tes yeux.

PARIS (AVANT TOI, APRÈS TOI)

1. APRÈS TOI

Si je désire une eau d’Europe, c’est la flache
Noire et froide où vers le crépuscule embaumé
Un enfant accroupi plein de tristesse, lâche
Un bateau frêle comme un papillon de mai.
A. Rimbaud

Rues larges comme places,
places illimitées comme le désert
et pourtant pleines de gens qui vont et viennent. Paroles
saisies à la volée ici et là
entre le bruit du monde et de “tout le monde”
dans une langue qui résonne obsédante et possédée
par un seul nom : Arthur Rimbaud.

Puis :

musées qui érigent un mystique, fantastique, protéiforme labyrinthe,
cathédrales ivres des symboles qui défient l’abîme,
lointains horizons normands, d’acier, de tours et de cavalcades,
les barricades, les flammes, les chansons, les cris sans fin
de la Révolution, Napoléon, la Seine qui coule
lente et rapide telle que le temps et après …

Et après ?

Et après
un fleuve, une mer, un naufrage, un tourbillon des choses
qui dans la mémoire confuse et illimitée s’échappent
tels que les feux jetés par un train en marche :
les nations, les explorations, les colonies, les empires,
les peuples, le populisme, l’individu, l’individualisme,
la technique, la science, le progrès, la république,
les démocraties, la Première Guerre Mondiale,
l’après-guerre, le communisme, le fascisme,
l’existence, l’existentialisme, la crise de ’29, le nazisme,
une autre Guerre Mondiale, encore,
un autre après-guerre, encore,
la reconstruction, la guerre froide,
le développement, le Mai du ‘68,
les jeunes du Mai,
le flux et le reflux
et après …

Et après …

….et après
pourquoi lutter
pur se souvenir d’autres choses
encore?

Ici
on peut trouver tout
– et partout ! –
de sorte que rien n’est jamais
vraiment
à rechercher.

* *

Loin
la Tour Eiffel s’estompe
comme derrière une fenêtre
où le souffle silencieux étend un voile :
ce sont les larmes à la pensée
que pendant des années et des années
juste tes yeux
ont vu ce ciel.

II.

PARIS AVANT

Moi qui trouais le ciel rougeoyant comme un mur
Qui porte confiture exquise aux bons poètes,
Des lichens de soleil et des morves d’azur ;
Qui courais, taché de lunules électriques,
Planche folle, escorté des hippocampes noirs,
Quand les juillets faisaient crouler à coups de triques
Les cieux ultramarins aux ardents entonnoirs ;
Moi qui tremblais, sentant geindre à cinquante lieues
Le rut des Béhémots et les Maelstroms épais,
Fileur éternel des immobilités bleues,
Je regrette l’Europe aux anciens parapets !
A. Rimbaud

Le ciel….

Le ciel comme aveugle,
comme en aigle…

Ce ciel
loin,
parti
et ainsi…

….perdu,
comme rendu
au désert obscurci,
endurci,
sans vie
de l’hiver.

Un sourire affaibli,
apeuré
franchit l’air morne.

Rigide,
engourdi
dans la caresse gelée du vent,
le front baissé
sous ce ciel bas,
sous la pluie lente,
trop lente,
trop fine
pour l’appeler pluie
et trop épaisse
pour croire vrai ce prodige nu
– se sentir perdu dans le brouillard –
en qui pourtant
follement
il croit.

Labiles éclats
de sable noir : voici
la dure Seine
où comme goélands à l’horizon
se perdent
les voix et les frémissements
des blancs bateau
débordant de gens
qui lui semblent heureux.

Il marche
lentement,
caressant doucement
les parapets.

Plongé dans le secret
de son interne silence,
immense,
il n’entend pas les bruits :
partout
il y a de gens
et il ne voit personne.

Distrait par des souvenirs
qu’il ne sait pas d’avoir
l’adolescent timide bégaie des phrases incertaines
en cette langue nasale
que l’enfant commença peut-être à apprendre
et que l’adulte finira pour oublier
presque entièrement.

Les marbres impassibles,
Notre-Dame
impossible.

Un visage qu’il sait de ne pas connaître
– et qui pourtant il pense de reconnaître –
s’évanouit derrière le coin,
tandis que comme en proie à la fièvre il parcourt
les vastes labyrinthes du Louvre,
où à la fin chaque couloir bifurque
en ères perdues,
symboles incompréhensibles,
dieux et fois surréels,
gouffres d’événements et temps qui fondent
puis
parmi les labyrinthes du trafic,
dans le gouffre des rues
et des places gigantesques
dont presque il ne peut pas imaginer
l’énorme traversée,
les yeux éclipsés sur la vitrine obscurcie où
son vain reflet scrute celui
encore plus vain,
encore plus inhumain
de la Tour Eiffel
qui grimpe vers ce ciel
désormais tellement
loin
et tellement….

….perdu…

…éthéré,
comme dispersé
dans le désert de pierre,
de verre
de l’hiver.

Une saison à l’enfer terminait,
une autre commençait
interminablement.

Je fumais des Gauloises,
je buvais du cognac,
je pensais de chercher un autre Ailleurs
– désespérément –
mais comme un héros
fatigué et d’un autre âge
j’étais en train de revenir à la maison
et je ne le savais pas.

TES VALISES

Un coup de ton doigt sur le tambour décharge tous les sons et commence
la nouvelle harmonie.
Un pas de toi, c’est la levée des nouveaux hommes et leur en-marche.
Ta tête se détourne: le nouvel amour! Ta tête se retourne: le nouvel
amour!
« Change nos lots, crible les fléaux, à commencer par le temps », te
chantent ces enfants. « Élève n’importe où la substance de nos fortunes et
de nos vœux”, on t’en prie ».
Arrivée de toujours, tu t’en iras partout.
A. Rimbaud

Ta légèreté, tes valises, tes départs, comme je les envie !
Et je sais d’être fou. Parce que l’envie c’est la folie même.
Peut-être que l’air, l’eau et le pain
sont tout ce qu’il y à envier dans ce monde
et le reste – tout le reste – sont des fables au vent.
Je le sais trop bien tout cela, et je le répète. Et pourtant
je t’envie quand même.

Ta légèreté, tes valises, tes départs, comme je les admire !
Je les vois aller sur la surface inutile du temps
comme un magique poisson volant
qui vaguement rebondit sur les vagues
par toi béni tantôt ici, tantôt là-bas, après
qui sait où….

Je ne peux même croire
ou imaginer
que celles-ci ne soient rien d’autre
que tes chaines,
ton fardeau,
ton tourment,
ton destiné exile de toi-même
comme il est pour moi-même
de rester ici
où je ne suis pas.

Invalid Displayed Gallery

Gabriele Venturi

ANNEXE :

INTERLUDE

A S.

Ah ! cette vie de mon enfance, la grande route par tous les temps, sobre surnaturellement, plus désintéressé que le meilleur des mendiants, fier de n’avoir ni pays, ni amis, quelle sottise c’était. – Et je m’en aperçois seulement !
A. Rimbaud

Varsovie.

Varsovie couverte de neige
et d’invisibles fleurs
que des blancheurs illimités
de la neige se nourrissent
et resplendissent
émerveillées.

Varsovie de le ghetto,
de le carnage.
Varsovie mil fois balayée
et mil fois
comme moi
ressuscitée.

Varsovie ta patrie
ton ciel.
Varsovie dans tes yeux
dans mon amour
comme un voile.

Varsovie de ton rire d’argent
et de ces intimes souffrances
dont je ne souffre pas plus
que presque sont oubli.
Varsovie des pas qui retentissent
dans le silence de spectres d’une rue latérale,
d’une vie quelconque qui passe
fatiguée de tristesse
et dont après personne
jamais ne saura rien.

Varsovie encore en vie
pourtant
sous en déluge de temps
que jamais se retient.

Varsovie
qui s’éloigne
comme une vallée dans une évanescence
des brumes sans destin,
vague labyrinthe
où le cœur
s’égare,
cherchant sens cesse ce qui reste
d’en son perdue et splendide
doleur.

Varsovie,
je le sais,
désormais presque seul en nom
qui dan le ténue s’évanouir de la mémoire
s’évanouit et s’attenue
comme ton visage
dans une pénombre d’une tonnelle en été,
fixant un coin obscure,
là ou je voudrait
rencontrer tes yeux